The entropic contributions in vitamin B₁₂ enzymes still reflect the electrostatic paradigm

Significance

The origin of the catalytic power of B₁₂ enzymes has been a major puzzle despite our previous finding that this effect is due to electrostatic stabilization of the leaving group. Recent findings of very large entropic contributions to catalysis were presented as an alternative to the electrostatic idea. Here, we use our ability to evaluate entropic contributions by the restraint release (RR) approach to reexamine the nature of the catalytic effect. The RR approach reproduces the observed entropic contributions to the activation barrier and demonstrates that the entropic effect is due to the previously identified electrostatic factors. Thus, we have further substantiated our paradigm for the origin of the catalytic power of B₁₂ enzymes.

Abstract

The catalytic power of enzymes containing coenzyme B₁₂ has been, in some respects, the “last bastion” for the strain hypothesis. Our previous study of this system established by a careful sampling that the major part of the catalytic effect is due to the electrostatic interaction between the ribose of the ado group and the protein and that the strain contribution is very small. This finding has not been sufficiently appreciated due to misunderstandings of the power of the empirical valence bond (EVB) calculations and the need of sufficient sampling. Furthermore, some interesting new experiments point toward entropic effects as the source of the catalytic power, casting doubt on the validity of the electrostatic idea, at least, in the case of B₁₂ enzymes. Here, we focus on the observation of the entropic effects and on analyzing their origin. We clarify that our EVB approach evaluates free energies rather than enthalpies and demonstrate by using the restraint release (RR) approach that the observed entropic contribution to the activation barrier is of electrostatic origin. Our study illustrates the power of the RR approach by evaluating the entropic contributions to catalysis and provides further support to our paradigm for the origin of the catalytic power of B₁₂ enzymes. Overall, our study provides major support to our electrostatic preorganization idea and also highlights the basic requirements from ab initio quantum mechanics/molecular mechanics calculations of activation free energies of enzymatic reactions.

Despite compelling evidence that electrostatic effects give the largest contributions to enzyme catalysis (e.g., refs. 1–3), some workers still believe that many different effects have been exploited in the evolution of enzyme rate acceleration (e.g., ref. 4). One of the most prominent proposals for nonelectrostatic catalytic effects involves the strain hypothesis (e.g., refs. 4 and 5), where it has been assumed that the enzyme destabilizes the ground state of the reacting system and consequently reduces the activation barrier for the chemical step. Early analyses of the catalytic power of enzymes containing the coenzyme B₁₂ cofactor (for review, see ref. 6), have provided major support for the strain hypothesis. More specifically, during the reaction of B₁₂ enzymes, the Co–C bond of B₁₂ is cleaved, leading to the formation of the 5′-deoxadenosyl radical and Cob(II)alamin, with a subsequent (or concerted) hydrogen transfer to the substrate. Some active sites and a generic free-energy surface for feasible reaction paths are depicted in Figs. 1 and 2, respectively. The rate of the nonenzymatic reaction of the Co–C bond cleavage is more than 10 orders of magnitude slower than the reaction catalyzed by B₁₂ enzymes (a more quantitative analysis is given in SI Text, section S1). The enormous catalytic effect has originally been assumed to present, what is, perhaps, the best support for the strain idea. This suggestion has emerged from the work of ref. 7 and, to some extent, from subsequent studies that modified this view (see below) but still kept the idea that strain energy plays a major role in the catalysis of these enzymes.

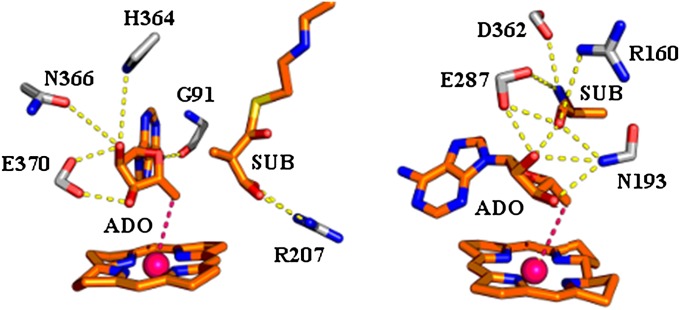
Fig. 1.

The reacting system and stabilizing residues in the TSs of MCM (Left) and EAL (Right).

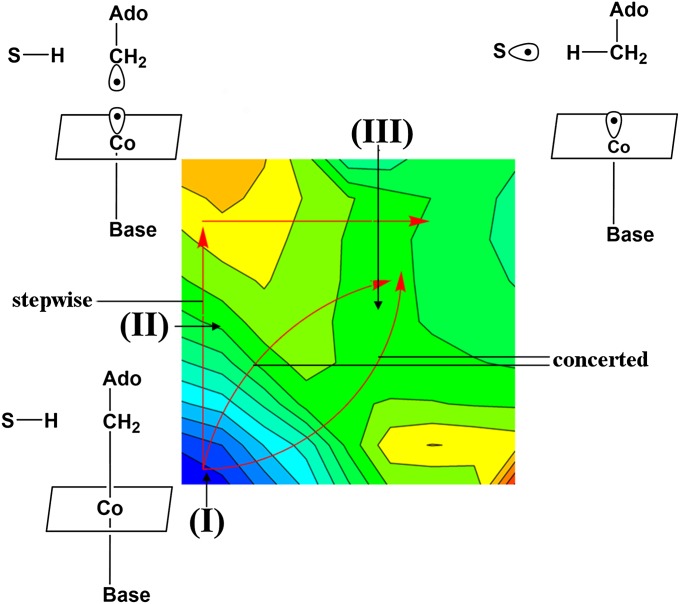
Fig. 2.

The alternative paths for the first steps of the reaction catalyzed by MCM and EA. The configurations I, II, and III are considered in the entropy calculations.

Although most support of the strain proposal has greatly decreased (for review, see ref. 8), it seems that, despite the great progress in structural (e.g., refs. 9 and 10), biochemical, and chemical studies (for review, see ref. 6), it is still hard to determine the origin of the catalytic effect by the available experimental information. The main problem is the need to determine the relative importance of different energy contributions, and it is not clear how to obtain a unique energy decomposition from experimental studies.

In principle, it is possible to explore catalytic effects of B₁₂ enzymes by quantum mechanics/molecular mechanics (QM/MM) approaches (e.g., refs. 11–18), and some of the progress made by such studies (as well as the problems in some of them) has been outlined in ref. 8 and below. Apparently, despite the insight provided by the above calculations, they have not determined conclusively the relative importance of the different catalytic factors. That is, calculations of strain energy by minimizing the energy of a many-atom protein system are extremely problematic. This problem is associated with the large dimensionality and the interplay between protein deformation and the substrate-assumed strain. Proper analysis must involve extensive sampling (see ref. 19 for a related problem) and is unlikely to be obtained by QM/MM energy minimization studies (see a related analysis in ref. 20). The best way is to use very extensive free-energy calculations of the reaction profile and then to estimate the energy contributions by the linear response approximation or related approaches. At present, the empirical valence bond (EVB) approach offers probably the best way to accomplish this task. Such a strategy was used in our previous study (8), where the catalytic free-energy contributions of B₁₂ enzymes were explored. This was done by starting with a very careful ab initio calculation of the surface of the reference solution reaction (Fig. S1 and more recent similar studies in Figs. S2–S5), then calibrating an EVB surface (using the reference solution reaction), and finally using this EVB surface to study the free-energy surface in the protein and in solution (Fig. S6). Our previous study established that the major part of the catalytic effect is due to the electrostatic interactions between the ribose of the ado group and the protein, but also found that the strain contribution is actually very small (SI Text).

Unfortunately, the reliability and the nature of the EVB calculations have not been fully appreciated as is apparent from a subsequent metadynamics (MTD) study (17) that will be addressed below. Furthermore, the fact that the EVB calculations have evaluated the total activation free energy rather than some enthalpy contribution has not been appreciated, or was simply overlooked. An instructive example is a recent experimental study of the catalysis in ethanolamine ammonia-lyase (EAL) from Salmonella typhimurium (21), which provided an interesting analysis of the catalytic action of B₁₂ enzymes. This study explored the activation entropy at very low temperature (234–248 K) and found about −18 kcal/mol contributions from −TΔS^#. It was argued that the catalytic effect of B₁₂ enzymes is due to entropic rather than electrostatic effects and it was assumed that our previous study (8) has involved only an enthalpy-based proposal (instead of a systematic converging free-energy calculation). The analysis of ref. 21 reflects significant problems, including attributing the entropic effect to an elusive landscape effect, and some unfamiliarity with the electrostatic concept. However, the experimental findings (related experiments will be discussed below) seem to present a fact that must be addressed in exploring the catalytic power of B₁₂ enzymes. In this respect, it is useful to note that, as we have found in our studies of alcohol dehydrogenase (22), the entropic effects can be very large at low temperatures and then be converted (in some cases) to enthalpy effects at room temperature, while having a nearly constant activation free energy. However, the most important finding of ref. 22 has been that entropic effects can reflect the electrostatic free energy associated with the interaction of the preorganized environment with the reacting fragments.

The finding that the catalytic effect of B₁₂ enzymes involves significant entropic contributions has also been reported in earlier studies. In particular, the study of methylmalonyl-CoA mutase (MCM) (23) found an activation entropy of 18.2 cal/mol at 310 K, where the corresponding −TΔS^# is −5.3 kcal/mol (a similar contribution appears at room temperature).

Overall, it has been suggested by the authors of the above experimental studies that B₁₂ enzymes catalyze their reactions using entropic effects. However, no clear explanation has been provided for the origin of the entropic contributions, and this problem has been compounded by the proposal of entropic contributions along the conformational coordinate (21), where the nature of the physical effect, which can lead to the presumed landscape, was not considered.

Results and Discussion

To determine the origin of the catalytic effect of B₁₂-containing enzymes, we must consider the relevant reference reaction in solution. As explained in detail elsewhere (e.g., ref. 2), the most meaningful reference reaction (as much as the effect of the enzyme environment is concerned) is a “chemistry-filtered” solution reaction that involves the same mechanism as the one used by the enzyme (namely the reaction described in Fig. 2). This reference reaction is taken as the reaction in which all of the reactants are at the same solvent cage. This is essential to eliminate the confusion associated with the trivial concentration effects that completely account for the probability of having the reactants in the cage. Here, one must accept the possibility that the reaction may be concerted and the fact that the overall solution reaction involves the process of bringing the reactants to the same solvent cage, which makes the experimental distinction between concerted and stepwise path (inside the cage) extremely challenging. Fortunately, the reference reaction can be explored computationally (see ref. 8 and SI Text, Figs. S1–S4), and the barrier for the limit of a stepwise path, where the bond breaking is rate limiting, is known experimentally (SI Text). Thus, following the analysis in SI Text, we can see that, for the concerted and stepwise reference reactions, the values of ΔΔg^# are 10 and 14 kcal/mol, respectively. The key question, however, is as follows: What is the origin of the catalytic effect? This issue will be addressed below.

Our study of the above problem started using as a model the reaction of MCM (9) (Protein Data Bank ID code 4REQ), because this system has been studied very carefully in our original work (8). The corresponding system is depicted in Fig. 1. The first step in our study involved running EVB simulations of the Co–C bond-breaking process in solution and in the active site of MCM, and the calculated EVB free-energy surfaces, summarized in Fig. S4, reproduced about 16 kcal/mol reduction in the activation barrier for the bond-breaking step ($\mathrm{\Delta }{\mathit{g}}_{\mathit{enz}}^{\mathrm{\#}}\mathrm{=}13$ kcal/mol, $\mathrm{\Delta }{\mathit{g}}_{\mathit{wat}}^{\mathrm{\#}}\mathrm{=}29$ kcal/mol). This accounts for the observed catalytic effect (for the bond-breaking step), as well as for a large reduction in the reaction free energy (ΔG_p = 3 kcal/mol and ΔG_w = 22 kcal/mol and also ΔG_p ≅ 11 kcal/mol for the stepwise bond-breaking process). Most importantly, our study established that the catalytic effect is associated with the interaction between the ribose and the protein polar and ionized residues [in particular, Glu-370, which is equivalent to Glu-330 in the mutase from Clostridium cochlearium (10)]. The finding that the catalysis is associated with electrostatic interactions rather than strain effects was established by us, using several approaches, ranging from showing that the catalytic effect disappears once we study the reaction without the electrostatic effects, to FEP calculations of the steric effect. It was also shown that the assessment of the steric effect could not be done without using converging free-energy calculations rather than energy minimization approaches. The important finding that the interactions between the 2′- and 3′-OH groups of the ribose with Glu-370 play a major role is also supported by the reduced activity upon removal of the 2′-OH group (24) and the loss of activity upon mutation of the equivalent Glu-330 in glutamate mutase (25).

The above discussion is basically a summary of what we have already established, whereas the focus of the current work is on the origin of the observed entropic effect. Here, we face a very significant challenge because calculations of entropic contributions converge very slowly (26) and exploring the origin of such contributions is even more demanding. Fortunately, our restrain release (RR) approach (e.g., refs. 27 and 28; SI Text and Fig. S5) offers a very powerful and effective way of evaluating entropic contributions. This approach (SI Text, section S6) restrains the system under study to sets of Cartesian coordinates and then evaluates the free energy of releasing the restraint. The RR free energy with the lowest absolute value then provides an estimate of the relevant −TΔS. The evaluation of the difference between the RR results at the transition state (TS) and reactant state (RS) provides the estimate for the entropic contribution to the activation barrier.

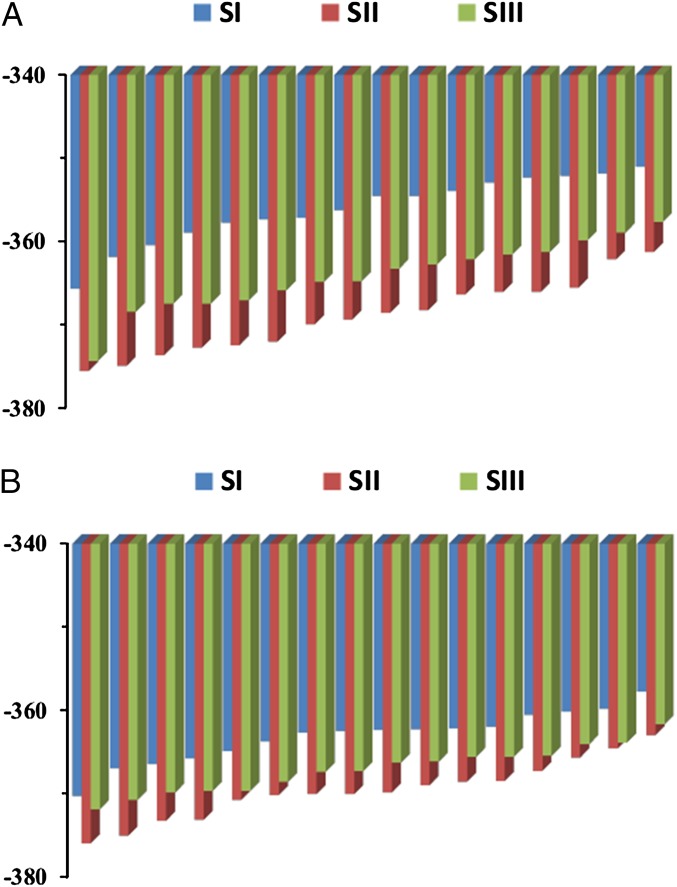
The results of the RR approach for MCM are summarized in Table S1 and Fig. 3A. The calculations considered the change in entropy between configurations I and II of Fig. 2 (the Co–C bond-breaking step) and between configurations I and III (where the hydrogen is being transferred). The activation entropy can be estimated as being between the two resulting values, instead of trying to locate the “actual” transition state and to estimate the activation entropy from state I to the actual transition state (see discussion at the end of SI Text, section S6). As seen from the table and the figure, we reproduce the trend of the observed effect (−TΔS^# of −5.3 kcal/mol and −10.2 to −6.6 kcal/mol for the observed and calculated contributions, respectively). Now we can ask what the origin of the entropic effect is. Here, we exploit the fact that the RR approach allows us to look for different contributions, and rerun the calculations, by setting to zero all of the residual charges of all atoms of region 1 (the ribose leaving group of the ado moiety and the substrate), as well as all protein residues that interact with them. The corresponding RR results, shown in Fig. 3B and Table S2, become much smaller with an estimate for −TΔS^# of −5.2 to −3.9 kcal/mol (instead of −10.2 to −6.6). The corresponding results indicate that the entropic effect reflects to a major extent the electrostatic interaction between the atoms whose charges were set to zero and their surroundings. The reason for this effect will be discussed below.

Fig. 3.

The RR results in bar representation for MCM at 300 K in states I, II, and III, where the atoms of the ado plus the substrate and their surroundings are charged and uncharged in (A) and (B), respectively. The RR entropies for each of the three configurations are obtained by taking the differences between the corresponding bars with the smallest absolute size, which, in the present arrangement, are the bars on the right.

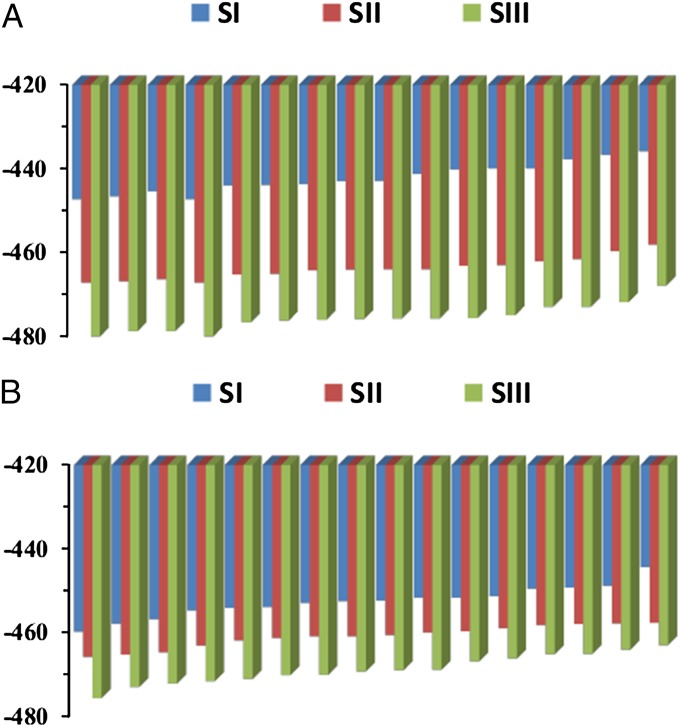
To further explore our conclusions, we moved to the EAL system studied in ref. 21 (and shown in Fig. 1, Right). Applying the RR approach to this system led to the results summarized in Fig. 4 and Table S3. Now we obtained much larger entropic contributions than those obtained in MCM. That is, the calculated −TΔS is −22.2 and −36.0 kcal/mol, respectively, for going from state I to state II and going from configuration I to III. This means that the calculated −TΔS^# is in the range of −22 to −36 kcal/mol, whereas the observed value is around −18 kcal/mol. Interestingly, we found that the entropic contribution for the I-to-II transition is smaller than the I-to-III transition (which is opposite than the trend in MCM). Although we have not performed careful FEP calculations for the reaction in EAL (our focus has been on the entropy), we note that this trend indicates that in the case of EAL we may have actually a stepwise reaction (where the bond breaking is rate limiting). Such a possibility is consistent with the fact that ref. 21 found no isotope effect in the case of EAL (so the concerted hydrogen transfer is not rate limiting). In this case, the relevant calculated value is the −22 kcal/mol.

Fig. 4.

(A) The RR results for EAL at 245 K (the same notation as in Fig. 3), where the atoms of the ado plus the substrate and their surrounding are charged, and (B) where all residual charges are set to zero.

Here again, we also evaluated the entropic effects when the residual charges of the leaving group, the substrate, and all surrounding protein residues within an 18-Å sphere were turned off (Fig. 4B and Table S4) and obtained a large reduction of the entropic contributions (now −TΔS for the transformation from configuration I to II is around −13.3 kcal/mol and for the transformation from configuration I to III is around −18.6 kcal/mol). We also like to note that the calculated $\left|-T\mathrm{\Delta }{S}^{\mp }\right|$ for the case when the charges are turned off is likely to be smaller upon inclusion of larger parts of the protein. At any rate, our calculations are consistent with the large observed entropic effect. As in MCM, this again indicates that the activation entropy reflects electrostatic effects.

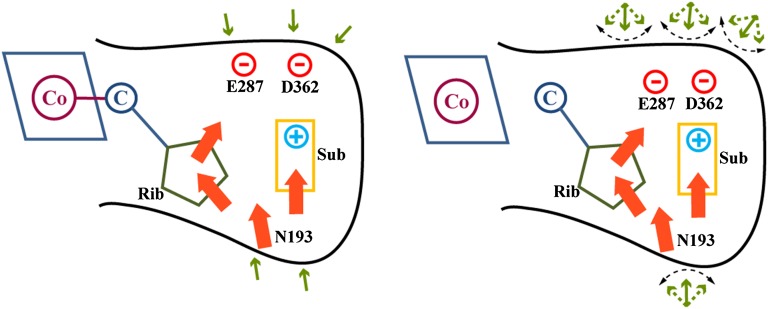
Reproducing the observed entropic contributions in two very different cases and different reactions indicates that we have captured the molecular origin of the entropic effect. In both cases, the entropic contribution reflects the electrostatic interactions (as is evident from the disappearance of a large part of this effect when the electrostatic interactions between the leaving group plus substrate and their surroundings are turned off). Now, one may ask what the molecular basis for the electrostatic entropic contribution is. Here, we believe that the main effect is described in Fig. 5. That is, moving from the RS to configuration II and III can be described as moving from separated polar and/or charged pairs to more closely bound pairs (as can be seen qualitatively from Table S5 and Figs. S6 and S7), with much smaller dipole moment and thus with smaller electric field on the surrounding groups (the groups outside the dashed line in Fig. 5). When we form the tight polar pairs, the external environment experiences less polar “solute” and is free to fluctuate, thus leading to a larger entropic effect (see the dipoles outside the dashed line in Fig. 5).

Fig. 5.

A schematic description of the origin of the entropic effect. The figure describes the situation in EAL by considering schematically the interactions between the leaving-group ribose (rib) plus the substrate (sub) and their first shell (explicit details are given in Fig. S5), while showing the response of the second solvation shell (the group outside the black solid line). The motion of the TS or state III results in stronger electrostatic interactions within the groups inside the solid black line and thus weaker interaction between theses groups and the polar groups in the second solvation shell. Thus, the bond-breaking process that involves an increase of the electrostatic interaction within the solid black line leads to weaker interaction with the second solvation shell, which starts to experience less polar solute, and is free to fluctuate more, thereby generating a larger entropic effect.

Concluding Remarks

Despite growing support for our idea that the main catalytic factor in enzymatic reactions is associated with electrostatic effects (e.g., see ref. 2), it is hard to exclude other effects by direct experimental studies, and a combination of experimental and theoretical studies is essential to reach unique conclusions about the validity of different proposals. B₁₂ enzymes have presented a challenge to the electrostatic idea because the reaction does not involve any significant change in charge distribution of the Co–C bond. However, our previous work (8) has indicated that the interaction between the ado leaving group and the enzyme active site changes drastically during the reaction and that the corresponding change in electrostatic free energy is the origin of the very large catalytic effect. Nevertheless, the findings of large entropic contributions to catalysis were presented, by some, as arguments against the electrostatic proposal. In this respect, it is useful to clarify again that, in contrast to the idea of ref. 21, our work has never been an enthalpy-based proposal, but a rigorous free-energy calculation. The ability to sample reaction surfaces to the level that evaluates entropic effects, which is, at present, unique to the EVB method, allows us to evaluate both activation free energies (which include entropic effects) and to calculate the isolated entropic contributions.

Of course, the focus of the current work is the analysis of the origin of the entropic contribution. Thus, after overcoming the challenge of reproducing the observed entropic trend, we addressed the main question, namely exploring the origin of this trend. Here, we established that the entropic contribution to catalysis of B₁₂ enzymes reflects electrostatic effects, in agreement with our previous study, where we found that the activation free energy is largely reduced because of electrostatic effects. Also note that our previous study (8) has established by FEP free energy calculations that all the catalytic effect is of electrostatic origin and that FEP calculations converge by far better than entropy calculations.

This work provides a powerful demonstration of the effectiveness of the RR approach in analyzing and reproducing delicate entropic contributions to enzyme catalysis. Accomplishing this task is almost unique to the combination of the EVB with either the RR approach or with a direct evaluation of the temperature dependence of the activation free energy with very long simulation time (29). That is, using regular classical simulations with the quasiharmonic approach is known by now to provide unreliable results (e.g., see refs. 30–32), partially because the relevant motion is not harmonic. In fact, even calculations of all of the contributions to binding entropies have not been accomplished in a reliable way by most approaches, with the exception of the RR approach (28). Trying to look on the harmonic contribution to the entropies of quantum mechanical activation barriers is equally problematic, because the use of ab initio QM/MM [QM(ai)/MM] vibrational frequencies is as problematic as the quasiharmonic approach and QM(ai)/MM does not allow one to have sufficient sampling for obtaining the activation entropy by, say, the RR approach.

In discussing the entropic contributions, we would like to clarify that the present entropic effect has very little to do with Jencks’ proposal of entropic contributions to enzyme catalysis (33). This proposal implies that the binding to the enzyme leads to a loss in the entropy of the substrate reacting fragments. Our previous studies demonstrated that Jencks’ and related proposals (e.g., ref. 34) used an incomplete thermodynamic cycle and incorrectly assumed implicitly that the motion of the reacting fragments is frozen at the TS. Furthermore, Jencks’ proposal predicted entropic catalysis for bond generation processes, whereas here we have a bond-breaking process.

At this point, it is also useful to clarify that the true catalytic effect of B₁₂ enzymes is not related to the cage effect pointed out by Finke (e.g., ref. 35) and considered in ref. 36 in discussing the entropic effects. That is, refs. 35 and 37 realized correctly that the progress of the reaction in water requires that the substrate will be in the same cage as the ado part to guarantee the hydrogen transfer (radical transfer) process. However, this issue has very little to do with the real puzzle of enzyme catalysis and it is exactly the reason for Warshel’s “chemistry-filtered” reference state definition (2). More specifically, the concentration effect needed to bring reactants to the same solvent cage has never been a puzzle, but a trivial concentration factor (of around 2.5 kcal/mol), which has always been considered rigorously in our cage effect (37), and was also identified correctly by early biochemical studies (e.g., ref. 38). The real question has been why the enzyme has a much lower activation free energy than the corresponding barrier for the reaction in a water cage. The fact that it is very hard to measure the concerted barrier in water is a problem for the experimental efforts but has never been the problem for theoretical estimates of the barrier.

Significant attention has been invested in arguing about the concreted versus nonconcerted paths. Here, it is important to clarify to the readers several points: Our study (8) has found, in agreement with a gas phase work (39), that the reference reaction involves a concerted path. In this respect, we like to clarify that the possibility that the least-energy path is concerted cannot be eliminated by current experimental studies, despite inconsistent attempts to argue so (e.g., refs. 17 and 18). For example, the attempt to support the stepwise surface by comparing the calculated isotope effect to the large observed effect (40) is unjustified, because one would expect large isotope effect for both the concerted path and the case where the hydrogen transfer is rate limiting. Note also that ref. 40 used a semiempirical model that has not been calibrated by ab initio surfaces. Furthermore, although ref. 40 seems to support the stepwise mechanism and was interpreted as such by some workers (e.g., ref. 18), no 2D concerted surface has been reported or examined.

Other theoretical attempts to exclude the concerted path have also been problematic (SI Text). For example, ref. 18 failed to generate a 2D surface or even to find a concerted TS in the protein with the so-called “our own n-layered integrated molecular orbital and molecular mechanics (ONIOM)” method (41). This problem is probably a reflection of the inability to properly relax the protein and the basic inconsistency of the ONIOM approach (see discussion in ref. 42). That is, the attempt to search a path in the protein is done with a very low-level semiempirical method and not with the ONIOM ab initio correction (the ab initio surface is never incorporated in the QM/MM surface inside the protein but added as an energy correction at the structures found by the semiempirical search). In contrast to the implications of ref. 18, our previous study has not added arbitrarily extra driving forces to the hydrogen transfer step but incorporated the result of well-known experimental findings about the radical transfer, which are extremely hard to capture by low-level ab initio models (see discussion in ref. 8). The same concerted features have now been captured by our current higher-level model without a correction (SI Text, Figs. S2 and S3), and the concerted path has remained the lowest energy path. Once our original solution surface has been transferred to the protein with very careful EVB calibration, and used with extensive sampling leading to a concerted path in the protein, it provides probably the most reliable protein free-energy surface currently available.

In further elaborating on the state of current theoretical studies, we would like to clarify that even the technically impressive (by the size of the QM region) results of the MTD study of MCM (17) has not been as reliable as one might tend to think (SI Text). Here again, the conclusion (17) that the surface cannot be concerted is problematic, as the actual calculated surface is quite flat in its diagonal range. As to reliability, we note (see above) that our strategy (e.g., ref. 8) of using very careful QM calculations in solution (with a higher-level QM model than that used in ref. 17) have produced a concerted path, and that moving the solution surface to the protein environment by a calibrated EVB model is expected to be more reliable (both in terms of the sampling and in terms of extrapolation of reliable reference systems) than the direct MTD in the protein site (see SI Text for more discussion). Finally, the problems with the MTD surface of ref. 17 also include the fact that the low level used does not produce correct radical transfer energies (as established in fact by other careful works of the authors of ref. 17).

It is useful to note that, in contrast to the impression of some (e.g., ref. 3), the importance of the electrostatic catalysis in B₁₂ enzymes could not be deduced consistently by approaches other than the EVB QM/MM calculations due to their inability to provide sufficient sampling. The pioneering work of Jensen and Ryde (14) was indeed the first to identify the electrostatic interactions but concluded that they are converted to “van der Waals” or “steric effects” (see discussion in ref. 8). We should also consider the recent ONIOM study (18) that has been presumed by its authors to be more accurate than the EVB and is, in fact, much less accurate than the ab initio calibrated EVB (SI Text). This work found incorrectly that the catalysis is due to a large steric and conformational effect [although the paper claims not to have reactant state destabilization (RSD), its actual calculated surface (see figure 2 in that paper) shows enormous RSD, which must be due to strain]. We believe that the calculated RSD reflects the inability of ref. 18 to sample and relax the protein configurations and thus drastically overestimates the steric effects (see example in ref. 43). A more detailed discussion of the problems associated with the strain hypothesis in B₁₂ enzymes is given in SI Text, section S4, including a careful and consistent calculation of the actual strain contribution (Table S6).

In conclusion, our study overcomes the major challenge in obtaining and reproducing the entropic contributions to the activation barriers in B₁₂ enzymes. This technical ability allowed us to demonstrate that the entropic effects are simply a part of the overall electrostatic catalysis.

Computational Methods

The elucidation of the free-energy contributions to the catalytic effect of B₁₂ enzymes present a major challenge that is hard to accomplish with molecular orbital QM/MM approaches due to the need of very extensive simulation times for sufficient convergence of the FEP. Separating between electrostatic and other contributions may present major problems even for FEP approaches. In our view, at present, the most effective way of addressing the B₁₂ problem is the use of the EVB method (1, 44), and this method was used in evaluating the reaction FEP for MCM (8). The main computational effort in this work is invested in entropy calculations. This is done by our RR approach (e.g., refs. 27 and 28), which is described in SI Text, section S6.