The role of turbulence in coronal heating and solar wind expansion

Abstract

Plasma in the Sun's hot corona expands into the heliosphere as a supersonic and highly magnetized solar wind. This paper provides an overview of our current understanding of how the corona is heated and how the solar wind is accelerated. Recent models of magnetohydrodynamic turbulence have progressed to the point of successfully predicting many observed properties of this complex, multi-scale system. However, it is not clear whether the heating in open-field regions comes mainly from the dissipation of turbulent fluctuations that are launched from the solar surface, or whether the chaotic ‘magnetic carpet’ in the low corona energizes the system via magnetic reconnection. To help pin down the physics, we also review some key observational results from ultraviolet spectroscopy of the collisionless outer corona.

1. Introduction

The origin of the Sun's supersonic and turbulent solar wind is linked intimately to the existence of the high-temperature (T>10⁶ K) solar corona. There is still no comprehensive understanding of the physical processes that generate both the coronal heating and the solar wind's acceleration. The early history of these unsolved problems reaches back more than a century [1,2]. Parker [3] combined many of the existing observational clues to synthesize a single-fluid model of time-steady acceleration, in which gravity was counteracted by the large gas pressure gradient of the million-degree corona. Just a few years later, Mariner 2 confirmed the existence of a continuous solar wind with roughly the properties predicted by Parker (e.g. [4]).

Early in situ measurements showed a range of plasma conditions at 1 AU, including: (i) a slow, dense and highly variable component (v≈300 km s⁻¹) that dominates in the ecliptic plane, (ii) calmer, but wave-filled high-speed streams (v≈700 km s⁻¹), and (iii) occasional explosive disruptions (‘coronal mass ejections’) accompanied by distorted fields and geomagnetic storms. Each of these phenomena was later found to correlate reasonably well with distinct solar features identified via remote sensing—e.g. (i) streamers and ‘quiet Sun’, (ii) coronal holes, and (iii) flares and active regions, respectively—but there are frequent exceptions to these general associations. The different coronal source regions have dramatically distinct appearances, plasma properties and spatial/temporal variability. Thus, it is likely that the heliospheric plasma that comes from these regions is energized by different combinations of mechanisms. In other words, there is probably not one single piece of physics that will ‘solve the coronal heating problem’ once and for all.

Much of the remainder of this paper will review the current state of debate regarding which physical processes are most active in the acceleration regions of the slow and fast solar wind. However, we do not want to overstate the degree of controversy. It is important to note that nearly everyone agrees on the following basic elements:

• (i) There is more than enough energy in the Sun's convective overturning motions to power the corona and solar wind.

• (ii) Convective granulation acts as a major ‘lower boundary condition’ for the injection of energy into the topologically complex magnetic field.

• (iii) Magnetic energy is (somehow) transported up to coronal heights and becomes organized into small-scale, nonlinear and largely field-aligned plasma structures.

• (iv) Magnetic and/or kinetic energy is (somehow) converted irreversibly to thermal energy by a combination of Coulomb collisions and collisionless wave–particle interactions. This conversion probably occurs most efficiently in regions with sharp spatial gradients of the plasma properties.

• (v) The high coronal temperature gives rise to a strong divergence of the pressure tensor, which in turn drives the dominant outward acceleration of the solar wind. Some other acceleration components are probably necessary to accelerate the fastest solar wind streams from coronal holes.

This paper presents a review of the authors' perspective on the above ideas and is not a comprehensive overview of the literature.

In §2, we discuss the importance of understanding the photospheric lower boundary condition in various turbulent coronal heating scenarios. Section 3 summarizes models based on the dissipation of waves and turbulent eddies along open field lines. Section 4 summarizes models based on magnetic reconnection and the opening up of closed loops. Section 5 reviews observations that point to efficient collisionless kinetic processes acting in the solar wind's acceleration region. Section 6 concludes with a brief summary of how studying turbulence in the solar corona has helped improve our broader understanding of other issues in astrophysics and plasma physics.

2. Photospheric energy sources

The Sun's visible surface is threaded ubiquitously by magnetic fields, and these fields are believed to expand out through the solar corona and fill the heliosphere. However, accurate and regular measurements of the magnetic field are possible only at the photosphere (with spectroscopic Zeeman splitting and other polarization diagnostics) and in distant regions sampled by in situ magnetometer probes. Our knowledge of the coronal magnetic field comes mainly from model-based extrapolation techniques (e.g. [5,6]).

On the largest spatial scales (of order 0.1 to 1 solar radii, R_⊙), the photospheric field is organized into low-order multipole components and active regions that are driven by the solar dynamo. On smaller scales of roughly 10⁻² R_⊙, the magnetic field becomes fragmented into the so-called supergranular network [7,8]. Below that is the convective-scale granulation, with rapidly evolving cell-like structures ranging between 10⁻⁴ and 10⁻³ R_⊙ in size. It is still not known whether the supergranulation is a manifestation of convective instability (i.e. just a ‘deeper’ kind of granulation), or whether it arises from other processes (e.g. [9,10]).

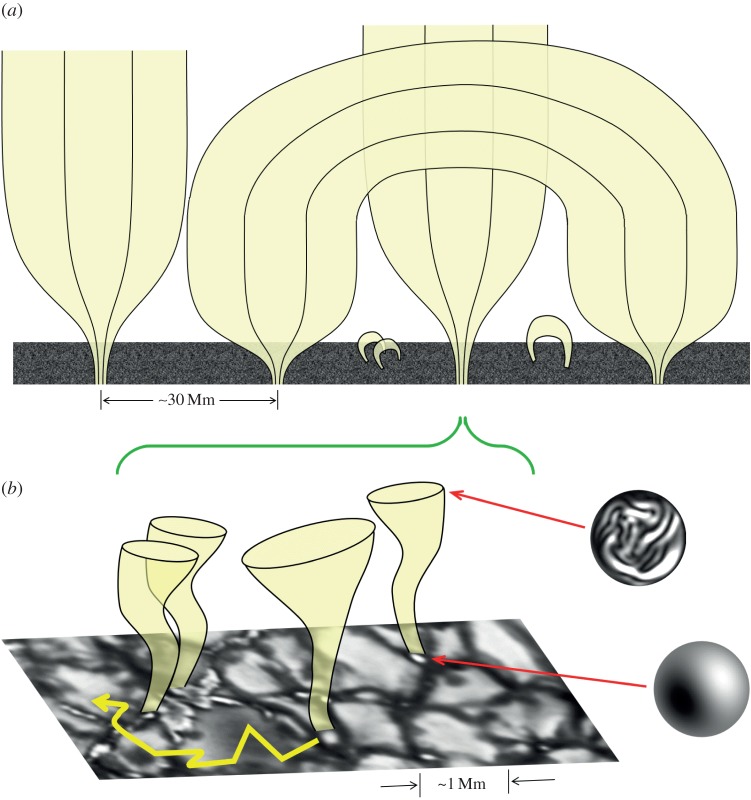
Figure 1 is a simplified illustration of how we believe the complex multi-scale magnetic field is organized in regions that feed the solar wind. The most fundamental building blocks appear to be the G-band bright points, i.e. thin flux tubes with field strengths of 1000–2000 G and diameters of 50–200 km that are herded into the dark downflow lanes between the granulation cells [16]. These flux tubes appear to be oriented in a nearly vertical direction, and they undergo cross-sectional expansion as the field strength decreases with increasing height. Their filling factor (i.e. the fraction of the solar surface they cover) grows from values less than 0.1–1% in the photosphere to a near volume-filling unity in the low corona. These features seem to be the ultimate ‘footpoints’ of nearly all larger scale coronal magnetic structures. Thus, the nature of their magnetohydrodynamic (MHD) variability is necessarily of prime interest when attempting to understand the evolution and dynamics of the coronal magnetic field.

Figure 1.

Cartoon representation of coronal magnetic field expansion, inspired by similar figures from Gabriel [8], Peter [11], Cranmer & van Ballegooijen [12] and Tian et al. [13]. (a) On supergranular scales the field is concentrated most strongly in the bright chromospheric network. Flux tubes expand laterally with increasing height to form a funnel/canopy structure. (b) On smaller scales, the field is concentrated into intergranular flux tubes that are jostled by convection and experience MHD turbulence. Granulation image adapted from Abramenko et al. [14], and turbulent flux-tube cross sections adapted from Asgari-Targhi et al. [15]. (Online version in colour.)

Intergranular bright-point flux tubes are jostled continuously by the evolution of surrounding granules. Isolated flux tubes undergo a random-walk type of motion [17], and occasionally one sees discrete jumps that may indicate the merging or fragmenting of unresolved components [18]. Some bright points execute classical Brownian (i.e. erratic and diffusive) random-walk motions, but others appear to move in a more vortex-like or rotational manner (e.g. [19]). In the so-called thin-tube limit [20], it is possible to decompose most observed bright-point motions into a superposition of transverse, incompressible kink modes. Cranmer & van Ballegooijen [12] showed how these kink modes gradually change their character to match the classical transverse Alfvén wave when the thin tubes become volume-filling at larger heights. Inside the flux tubes, the upward energy flux of Alfvén waves has been inferred to be about 3×10⁵ W m⁻². However, after taking into account the small filling factors, the surface-averaged photospheric flux is only about 2000 W m⁻² [12]. Nevertheless, this appears to be more than sufficient to balance radiative losses in open-field regions (e.g. [21]).

In addition to the above idea of magnetic flux tubes being buffeted and shuffled by granular motions, these bundles of magnetic field are also continuously emerging from below the photosphere. Away from active regions, much of this emergence takes the form of bipolar ‘ephemeral regions’ [22,23]. The individual poles of these regions tend to be advected to the edges of supergranular cells, where they coalesce to form the chromospheric network. Along the way, a combination of diffusive shuffling, tangling and magnetic reconnection with neighbouring regions helps to maintain the system in a dynamical steady state (e.g. [24]). We discuss the energetic consequences of this emergence and cancellation for coronal heating in §4.

There is some debate concerning the turbulent nature of the photospheric magnetic elements. High-resolution movies of individual granules often convey the appearance of quite ‘laminar’ overturning motions. The kinetic energy spectrum of horizontal bright-point motions is continuous in frequency space (e.g. [12,25]), but it does not necessarily show the power-law behaviour expected from an active cascade. Time-dependent MHD simulations of the chromosphere and corona (see §3) typically do not need there to be fully turbulent motions injected at the lower boundary, since a rapid cascade develops naturally above the photosphere. However, it is difficult to avoid the fact that the deep convection zone—host to the highly nonlinear solar dynamo—must be strongly turbulent [26]. Observations of the spatial diffusion of magnetic elements in the photosphere also show statistical properties similar to those seen in simulations of turbulent diffusion [14,27]. Further elucidation will likely come from the next generation of high-resolution solar observations, such as the Daniel K. Inouye Solar Telescope (DKIST) [28] and the Coronal Solar Magnetism Observatory (COSMO) [29].

3. Waves and turbulence in the open-field corona

The idea that the solar atmosphere is heated by the dissipation of upward-propagating waves has been studied for more than half a century (e.g. [30]). This remains a compelling explanation—especially for the open-field regions that connect to the solar wind—because the energy responsible for coronal heating must somehow propagate up to the heights where the heat is deposited into the plasma. In situ measurements have shown that the fast solar wind contains a dominant population of Alfvén waves [31] that propagate mostly away from the Sun. However, there has been uncertainty about whether Alfvén waves generated in the photosphere can damp out rapidly enough in the low corona to provide the required heating (e.g. [32]).

The last few decades have seen a gradual refinement in models that make use of waves and turbulence to power the solar wind [33–35]. The convection-driven jostling of flux-tube footpoints (see §2) may give rise to a range of MHD wave modes, but it is likely that the incompressible Alfvén mode undergoes the least amount of viscous and conductive damping to become the dominant wave type in the upper chromosphere and low corona. Alfvén waves that propagate along a flux tube with a radially varying Alfvén speed undergo partial reflection back towards the Sun [36,37]. The existence of counter-propagating wave packets—even if only a small fraction of the energy is coming back down—allows a nonlinear MHD turbulent cascade to develop [38–41]. The steady-state cascade rate of strong, imbalanced and anisotropic MHD turbulence determines the rate of dissipation, and thus the rate of coronal heating (see also [42–46]).

Cranmer et al. [47] described a project to build realistic, time-steady and one-fluid models of wave/turbulence-driven coronal heating in open magnetic flux tubes. In this numerical code, called ZEPHYR, the rate of partial wave reflection is computed from linearized non-WKB transport equations. The rate of wave dissipation (and plasma heating) is computed from expressions derived from a wide range of models of strong Alfvénic cascade with variable cross helicity (e.g. [48]). Once the turbulence physics is specified, the only freely adjustable parameters in ZEPHYR are the photospheric lower boundary conditions and the radial dependence of the flux tube's magnetic field. Cranmer et al. [47] found that a fixed choice for the photospheric wave properties yielded a realistic range of slow and fast solar wind conditions. More recently, this model has been extended to include a broader range of magnetic configurations [49,50] in order to explore how the properties of the solar wind depend on the corona's ‘superradial’ flux-tube expansion (see also [51,52]). Also, Cranmer [53] showed that wave/turbulence models can reproduce in situ ion charge states quite well if electron heat conduction in the low corona is treated realistically (i.e. following the non-classical development of weakly collisional suprathermal tails).

Despite the successes of time-steady models, they do not self-consistently simulate the actual process of MHD turbulent cascade at the heart of the proposed coronal heating scenario. Thus, fully time-dependent and three-dimensional models of reduced MHD turbulence were developed by van Ballegooijen et al. [54]. This simulation code, called BRAID, follows the development of turbulence in a flux tube rooted in the photosphere and driven by slow laminar internal motions.¹ Turbulence develops rapidly in the chromosphere and is transmitted into the corona (see cross sections shown in figure 1) despite the large degree of reflection encountered at the sharp transition region. The time-dependent models constructed so far (see also [15]) have largely validated the phenomenological cascade rate prescriptions used by ZEPHYR. Van Ballegooijen et al. [61] used the BRAID code to conclude that a family of quasi-static ‘direct current’ models of coronal heating should be ruled out. They found that waves and turbulence can give rise to a strongly dynamical type of twisting/braiding of coronal field lines, and this appears to be consistent with recent ultra-high-resolution imagery [62].

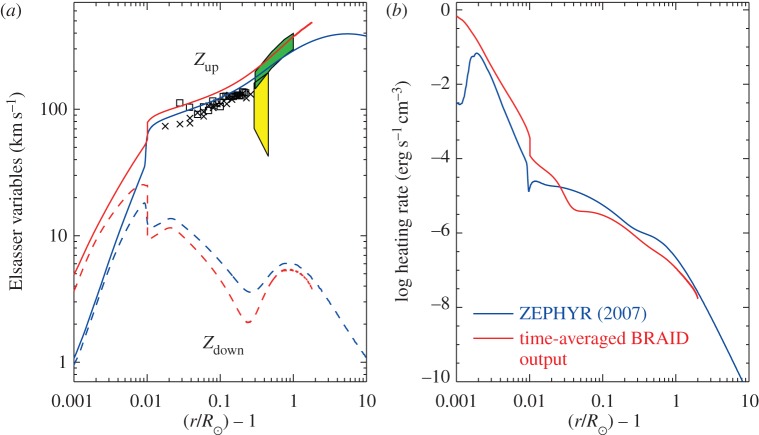
Figure 2 shows a preliminary comparison between the results of ZEPHYR and BRAID for a model of a polar coronal hole. The strongly fluctuating plasma parameters computed by BRAID were averaged in time and truncated at a height of 2 R_⊙ above the photosphere (above which it was assumed no incoming waves enter the system). There are similarities and differences between the two models that still need to be digested and understood. Note from figure 2a that there is some tension between different observational determinations of the Alfvén wave velocity amplitude at heights of 0.3–0.6 R_⊙ above the photosphere. Both Esser et al. [65] and Hahn & Savin [66] analysed the non-thermal broadening of ultraviolet emission lines observed above the solar limb and interpreted them in terms of unresolved Doppler ‘sloshing’ due to Alfvén waves. However, there is not enough information in the data to fully specify the full set of ion temperatures and wave amplitudes for any given collection of emission lines. These studies used different sets of assumptions—and different data analysis techniques—to estimate the wave amplitudes. It is still an open question whether the strong damping inferred by Hahn & Savin [66] actually exists.

Figure 2.

Comparison of the height variation of (a) Alfvén wave velocity amplitudes, expressed as Elsasser variables of upward Z_up and downward Z_down wave energy and (b) the turbulent heating rate, from BRAID (red curves) and ZEPHYR (blue curves). Also shown are observational data for Alfvén wave amplitudes, converted into Elsasser variables under the assumption that nearly all the energy is in Z_up: black X's [63], black squares [64], green region [65] and yellow region [66]. (Online version in colour.)

4. Magnetic reconnection in the open-field corona

It is clear from observations of the Sun's rapidly evolving ‘magnetic carpet’ [67] that much of the energy released in the low corona is due to complex interactions between neighbouring loop-like concentrations of magnetic flux. It is difficult to see any way around the idea that magnetic reconnection is going on continuously in the corona and converting magnetic free energy into heat. Additionally, many of the open flux tubes that reach into the heliosphere are rooted in the magnetic carpet, and their footpoints are often in close proximity to the rapidly evolving closed loops. Thus, it is natural to propose that some of the mass and energy of the solar wind is injected from closed to open flux tubes by reconnection (e.g. [68–71]).²

The idea of a reconnection-driven solar wind is relevant to a discussion of coronal turbulence, since the two phenomena (turbulence and reconnection) are nearly always seen in tandem. On the one hand, the rate of driven reconnection may be modulated—or even determined—by the properties of ‘background’ turbulence [77]. On the other hand, the dissipation of an MHD cascade is likely to be governed by the behaviour of spontaneously formed reconnection regions on kinetic scales (e.g. [78,79]). The situation is complicated by the fact that the Poynting flux associated with the emergence of closed-loop regions (which presumably drive the reconnection) is seen to be roughly 10³ W m⁻² [69], which is of the same order of magnitude as the Alfvén wave energy flux discussed above. Thus, it would not be surprising if the corona were heated by an inseparable combination of wave/turbulence dissipation and magnetic reconnection.

Observations of coronal plumes and jets provide evidence for the existence of discrete reconnection events in open-field regions [80,81], However, these bright and narrow features are identifiable in images, because they appear to occupy a small fraction of the coronal volume at any one time. We thus need to determine how much of the solar wind's total mass and energy is fed by these events. This is related to finding a way to measure the fraction of the corona's total ongoing reconnection that goes specifically into opening up previously closed fields. Cranmer & van Ballegooijen [82] studied these issues with Monte Carlo simulations of the time-varying magnetic carpet and its connection to the large-scale coronal field. These models showed that reconnection and loop-opening processes on supergranular scales may be responsible for the observed jets, but probably not for the majority of ‘bulk’ solar wind acceleration. The Cranmer & van Ballegooijen [82] models were limited in scope because they approximated the evolving corona as a succession of potential-field states, but subsequent non-potential models (e.g. [83]) have found similar results.

Recently, there have been several other studies of how magnetic reconnection may indirectly affect the energization of solar wind plasma even if it does not provide the bulk of the thermal energy. Bursty reconnection events may be an additional source of MHD waves in the corona [84,85]. Even if reconnection does not send a substantial energy flux into the solar wind, it may help to ‘fill in’ the low-frequency part of the Alfvénic fluctuation spectrum. Periods longer than about 30 min are inferred to exist from the in situ data but are not found in models that rely only on granular buffeting in the photosphere. An alternative set of ideas was suggested by Antiochos et al. [86], who highlighted the existence of topologically complex corridors of open fields rooted in distorted quasi-separatrix layers. These regions trace out a convoluted boundary between open- and closed-field regions, and the forcing of the magnetic carpet leads to its continual rearrangement. Reconnection-driven loop opening is likely to occur in these regions, and Antiochos et al. [86] suggested this ‘separatrix web’ is a major driver of the chaotic and dense slow wind.

5. Physical insights from ultraviolet spectroscopy

Many important clues about the physical processes responsible for heating and accelerating the solar wind have come from ultraviolet spectroscopy. Because of the rapid decrease in density with increasing height, Coulomb collisions become infrequent in the extended corona.³ Thus, at a sufficiently large height, each ion species may end up with a different temperature and flow speed, and may even exhibit its own unique type of departure from an isotropic Maxwellian velocity distribution. This makes the collisionless outer corona a key place to discriminate between different theories, since each process is likely to suggest different rates of energization as a function of ion charge and mass. This section provides a brief ‘top-10 list’ of results from the Ultraviolet Coronagraph Spectrometer (UVCS) [87,88] that have helped to elucidate the properties of waves and turbulence in the extended corona. UVCS operated aboard the Solar and Heliospheric Observatory (SOHO) spacecraft from its launch in December 1995 until the instrument's shutdown in January 2013. Other useful reviews of the UVCS mission include those by Noci et al. [89], Huber [90] and Antonucci et al. [91].

(a). Fast wind from coronal holes

• 1. UVCS observations of the bright O VI 103.2, 103.7 nm emission lines indicated that the associated O⁺⁵ ions are much more strongly heated than protons in polar coronal holes. Detailed analyses of the line profile shapes and intensity ratios point to perpendicular temperatures T_⊥≈2×10⁸ K, roughly two orders of magnitude hotter than the protons, and large temperature anisotropy ratios T_⊥/T_∥ possibly greater than 10 [87,92,93]. Measured kinetic temperatures of both O⁺⁵ and Mg⁺⁹ ions are greater than ‘mass-proportional’ when compared with protons, with T_i/T_p>m_i/m_p. These conditions are reminiscent of the predicted properties of ion cyclotron resonance in a collisionless plasma. Thus, the UVCS results helped to drive a resurgence of interest in this mechanism in the fast wind (e.g. [94–97]).

• 2. UVCS line profile measurements in coronal holes also led to the conclusion that the fast solar wind is accelerated closer to the Sun than was believed in prior decades. This kind of determination is made possible by the fact that resonantly excited lines undergo ‘Doppler dimming’, i.e. they are sensitive to motions transverse to the line of sight and thus mostly parallel to the off-limb magnetic field. Strachan et al. [98] used sounding rocket data to infer a supersonic speed (v≈200 km s⁻¹ at r≈2 R_⊙) for protons in a coronal hole. UVCS then made it possible to determine that the outflow velocity for O⁺⁵ ions grows even faster than the outflow velocity for protons. By r≈3–3.5 R_⊙, the heavy ions are flowing faster than the ‘bulk’ solar wind by as much as a factor of two [87,92,93,99].

• 3. In polar coronal holes, the densest concentrations of bright plumes are seen to have higher densities, lower temperatures and lower outflow speeds than the dimmer ‘interplume’ regions (e.g. [87,100,101]). Many impulsive polar jets have similar properties to the longer lived plumes [102]. However, there may be observational selection effects at work, since the UVCS counterparts to jets first identified by Hinode at X-ray wavelengths seem to show hotter protons than in the surrounding regions [103]. Even if the coronal response at large heights is variable, the ultraviolet observations of jets appear to be consistent with models [104] in which a short burst of heating occurs at the base then fades away with time. These features may be a prime example of regions in which both reconnection and turbulence are acting together.

• 4. UVCS measured the properties of other types of coronal holes that appear and disappear at various times throughout the 11-year solar cycle. Miralles et al. [105] found that large equatorial holes undergo more gradual solar wind acceleration than the polar holes, but they both eventually reach high speeds (v>600 km s⁻¹) at 1 AU. Statistical studies of coronal holes at all latitudes show a strong correlation between O⁺⁵ temperatures and outflow speeds [106,107], indicating that the preferential perpendicular heating is tightly coupled with strong differential acceleration of heavy ions.

(b). Slow wind from streamers

• 5. Much of the low-speed solar wind appears to be associated with bright helmet streamers. White-light images show most streamers having a closed-field ‘core’ surrounded by ‘legs’ that are open to the solar wind, often topped by a converged radial ‘stalk’. UVCS Doppler dimming measurements at solar minimum [108] revealed the legs of large equatorial streamers to be a primary site of slow-wind-like outflow, whereas their large central cores did not show signs of bulk acceleration. Above the largest height of closed-field loops, O⁺⁵ ions in streamer stalks were seen to have similar preferential heating characteristics as their cousins in coronal holes [109]. Also, Strachan et al. [110] found some key correlations in streamers between UVCS plasma parameters and the relative rates of magnetic flux-tube expansion, which Wang & Sheeley [111] suggested could be a controlling factor in solar wind acceleration. These correlations must be confronted and explained by any successful model; for an initial comparison of this type, see Abbo et al. [112].

• 6. Raymond et al. [113] found that the elemental abundances of heavy ions in streamer legs match those seen in situ in the slow wind. However, in the closed-field cores the abundances are depleted by more than an order of magnitude [114,115]. This has been cited as evidence for gravitational settling, which begins to occur when Coulomb collisions are not fast enough to keep the ions mixed with the dominant hydrogen plasma. Because the settling effect alone would have depleted the abundances by much more than is seen, however, Raymond [114] suggested that streamers are likely to host some additional process that continuously mixes ‘fresh’ plasma into the streamer core. Coulomb drag and interchange reconnection may contribute to the cross-field mixing, but turbulence is also a strong candidate. Ubiquitous non-thermal line widths of order 30 km s⁻¹ in the low corona point to Alfvén-like fluctuations either as the means of additional spatial transport, or as a source of turbulent pressure that could support the ions in a non-hydrostatic equilibrium.

• 7. UVCS measurements of non-equatorial streamers have shown significant variation in their plasma properties. Some mid-latitude streamers associated with active regions were seen to have lower ion temperatures, but higher electron temperatures, than large ‘quiescent’ solar-minimum streamers [116–118]. The reasons for these differences may be explainable with a newer classification that is based on magnetic polarity: classical streamers with opposite-polarity footpoints (topped by null-point cusps) appear to have distinct properties from the so-called pseudostreamers with like-polarity footpoints (e.g. [119]). Efforts are underway to identify the remote-sensing and in situ data that best distinguish these structures from one another and identify the relevant physical properties at work [120].

(c). Coronal mass ejections

• 8. Coronal mass ejections (CMEs) are magnetically driven eruptions that are believed to involve the expansion of twisted ‘flux ropes’ into the heliosphere. UVCS provided the first real diagnostics of the physical conditions in CME plasmas as they accelerate through the corona. Specifically, UVCS data helped to determine that CMEs must undergo substantial heating [121,122], and in some cases the input thermal energy even exceeds the bulk kinetic energy. It is possible that similar kinds of turbulent cascade and dissipation occur in both CMEs and the background solar wind [123], or that these highly twisted, non-potential structures may dissipate energy via turbulent hyperdiffusion [124]. In any case, measurements of CME total energy budgets are key constraints to determining the dominant processes at work in these events.

• 9. Many models of CME formation predict the development of an elongated current sheet trailing behind the flux rope [125]. When these reconnecting features exist, there may be significant mass and energy injection into a CME's outer sheath. UVCS observed these current sheets in the emission of high-ionization species such as Fe⁺¹⁶, Fe⁺¹⁷ and Ca⁺¹³ [121,126,127]. In some cases, the width of the current sheet was found to be consistent with an anomalously large resistivity (e.g. [128,129]), which may also be consistent with theories of turbulent reconnection [77].

• 10. In a few events, UVCS detected the presence of a supra-Alfvénic shock in front of a fast CME (e.g. [130,131]). Independent measurements of the shock speed and electron density (from Type II radio bursts) allow the coronal Alfvén speed, shock Mach number and compression ratio to be determined. Also, the rapid broadening of some emission lines seen by UVCS indicated preferential ion heating and relatively weak electron heating, which has been predicted in some kinetic models of collisionless shocks [132].

6. Conclusion

The goal of this paper has been to review the progress made in recent years in viewing the processes of coronal heating and solar wind acceleration through the lens of MHD turbulence. There are viable models that can explain the energization of the open-field plasma as a result of the dissipation of propagating waves and turbulent eddies. There are also (somewhat less developed, but still plausible) models that invoke magnetic reconnection and the opening up of closed loops into the heliosphere. Despite several decades of useful observational constraints, we still have not yet pinpointed what specific measurements will convincingly identify the dominant physical processes. Nevertheless, it is clear that telescopes have not yet achieved the necessary spatial and time resolution to see how the most fundamental structures (e.g. flux tubes, turbulent wave packets) exchange energy in the solar atmosphere. Also, we realize that there is a pressing need to bridge the ‘field-of-view gap’ between the historically separated domains of remote sensing and in situ exploration. Inner heliospheric missions like Solar Probe Plus [133] and Solar Orbiter [134] will lead this charge in the coming decade (see also [135]). We also hope that next-generation ultraviolet coronagraph spectrometers (e.g. [136]) may be developed in order to follow up on the successes of UVCS and extend the remote-sensing field of view to larger heights.

From a theoretical viewpoint, one physical process that deserves additional attention is compressibility. Many of the models discussed above have been limited to the mainly Alfvénic, low plasma β limit in which density fluctuations are either unimportant or completely ‘passive’. However, off-limb observations show that compressive fluctuations propagate up in open-field regions, along with Alfvén waves (e.g. [137,138]). The passage of Comet Lovejoy through the low corona revealed the existence of sharp density striations [139], and the relevant cross-field length scales are of the same order of magnitude as the expected turbulence correlation length. There have also been time-dependent MHD simulations in one [140] and two [141] dimensions that show Alfvén waves being converted efficiently into fast or slow compressive modes. Although the restricted dimensionality of these models is likely to be preventing the most efficient mode of reduced-MHD cascade from occurring (e.g. [142]), there may be regions of the corona that do support this kind of mode conversion.

Lastly, we believe it is worthwhile to summarize how an understanding of turbulent physics in the corona is important in a broader context. A clear practical benefit from a better model of solar wind acceleration is the possibility of improving long-term space weather forecasts (e.g. [143]). A different technological connection—involving the phenomenon of ion cyclotron resonance—may bear fruit in new designs for ion-based rocket propulsion systems [144]. Of course, identifying and characterizing the physical processes at work in the solar corona is useful in establishing a baseline of knowledge that can be applied to other stars and more distant astrophysical systems. For example, plasma heating from an MHD turbulent cascade has been suggested as being relevant to models of the interstellar medium [145], T Tauri stars [146], exoplanet atmospheres [147] and accretion discs around compact objects [148].

7. Funding statement

S.R.C.'s work was supported by NASA grant nos. NNX-10-AC11G and NNX-14-AG99G, and NSF SHINE program grant no. AGS-1259519. M.P.M.'s work was supported by NASA grant nos. NNX-06-AG95G, NNX-09-AH22G and NNX-10-AQ58G. The SOHO mission is a project of international cooperation between NASA and ESA.