Figure 2.

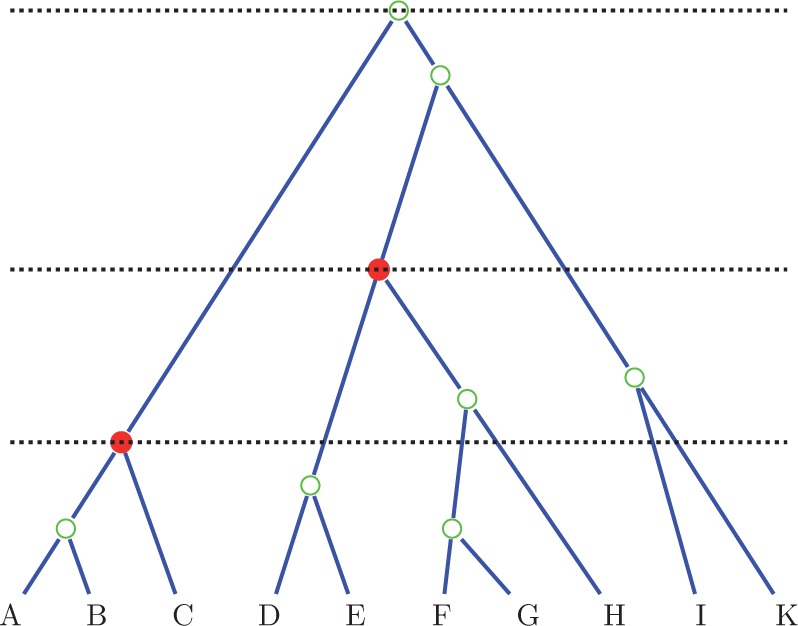
Counting ranked topologies. To count the number of ranked topologies for the tree depicted, we multiply the counts in the three levels. In the lowest level, we have three lineages reducing to one (root of lowest calibration), five lineages reducing to three and two free lineages not reducing. Hence, the total number of topologies is ${\text{R}}_3^1{\text{R}}_5^3{\text{R}}_2^2\left(\begin{array}{c}2+5+2-(1+3+2)\\ 1,2,0\end{array}\right)=3\times (10\times 6)\times 1\times \frac{3!}{1!2!0!}=540$. Note that in the multinomial we use one less lineage (two instead of three) for the calibrated clade, because its position as root is fixed. In the second level, we have three lineages reducing to one, and three free lineages reducing to two, giving ${\text{R}}_3^1{\text{R}}_3^2\left(\begin{array}{c}2+3-(1+2)\\ 1,1\end{array}\right)=3\times 3\times \frac{2!}{1!1!}=18$ and in the last level three lineages to one in three ways. Hence, the total number is $540\times 18\times 3=29,160$.