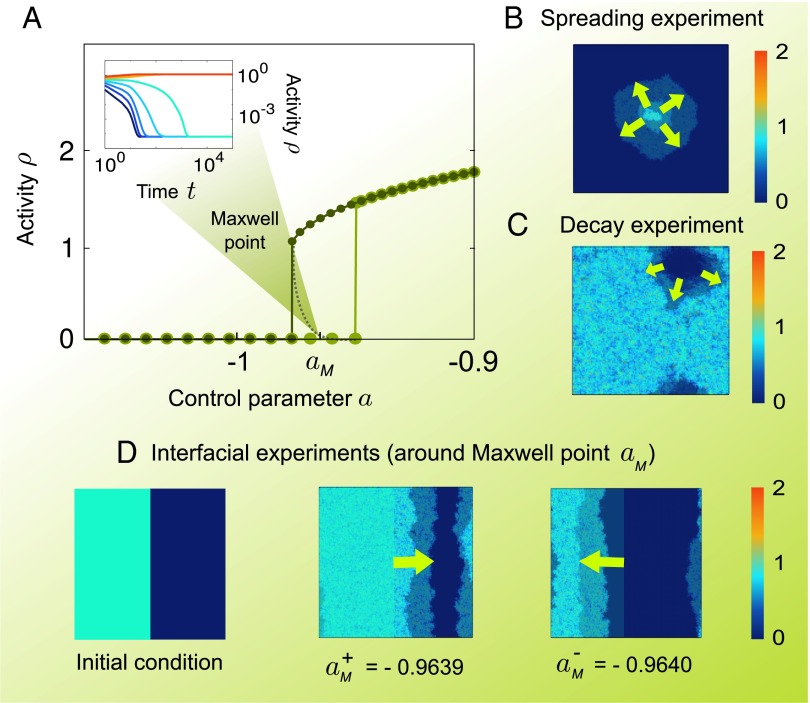
Fig. 2.

Computational results for Eq. 2 in a 2D lattice, showing an abrupt regime shift. Parameter values are $D=c=1$, ${\sigma }^2=1$, and $b=-2$. (A) Steady-state averaged activity as a function of the tunable parameter a (different colors correspond to different type of initial conditions: light green for small initial activities and dark green for large initial activities). There are two distinct stable solutions: one with an associated large stationary activity (which disappears around $a\approx -0.98$) and a trivial or quiescent one with $\rho =0$ (which becomes unstable at some point near $a\approx -0.95$). These two alternative steady states are separated by a line of unstable solutions (dashed gray). In the interval between the two limits of stability, two alternative stable states compete. The existence of bistability is confirmed by results in the inset, showing that the steady state depends upon initial conditions ($a=-0.9640$). B illustrates how an initially localized seed of activity expands throughout the system (spreading experiment) near the threshold of instability of the quiescent phase. Similarly, C illustrates the decay of an initially homogeneous state toward the quiescent state (decay experiment). (D) In interfacial experiments, half of the system is initially occupied and half is empty (Left); either the active phase invades the quiescent one (Center) or vice versa (Right). These two regimes are separated by a Maxwell point at which the interface does not move on average. In B–D, arrows indicate the direction of system’s advance with time.