Four wave mixing experiments with extreme ultraviolet transient gratings

Abstract

Four wave mixing (FWM) processes, based on third-order non-linear light-matter interactions, can combine ultrafast time resolution with energy and wavevector selectivity, and enables to explore dynamics inaccessible by linear methods.^1-7 The coherent and multi-wave nature of FWM approach has been crucial in the development of cutting edge technologies, such as silicon photonics,⁸ sub-wavelength imaging⁹ and quantum communications.¹⁰ All these technologies operate with optical wavelengths, which limit the spatial resolution and do not allow probing excitations with energy in the eV range. The extension to shorter wavelengths, that is the extreme ultraviolet (EUV) and soft-x-ray (SXR) range, will allow to improve the spatial resolution and to expand the excitation energy range, as well as to achieve elemental selectivity by exploiting core resonances.^5-7,11-14 So far FWM applications at these wavelengths have been prevented by the absence of coherent sources of sufficient brightness and suitable experimental setups. Our results show how transient gratings, generated by the interference of coherent EUV pulses delivered by the FERMI free electron laser (FEL),¹⁵ can be used to stimulate FWM processes at sub-optical wavelengths. Furthermore, we have demonstrated the possibility to read the time evolution of the FWM signal, which embodies the dynamics of coherent excitations as molecular vibrations. This result opens the perspective for FWM with nanometer spatial resolution and elemental selectivity, which, for example, would enable the investigation of charge-transfer dynamics.^5-7 The theoretical possibility to realize these applications have already stimulated dedicated and ongoing FEL developments;^16-20 today our results show that FWM at sub-optical wavelengths is feasible and would be the spark to the further advancements of the present and new sources.

In FWM three coherent fields interact into the sample via the 3^rd order susceptibility (χ⁽³⁾), which, differently to the 2^nd order one, does not vanish by reason of the sample symmetry;^1,2 FWM processes thus represent the lowest order (non vanishing) optical nonlinearity for most materials. The FWM concept is at the basis of many coherent non-linear methods, such as coherent Raman scattering, multidimensional spectroscopy, impulsive stimulated Rayleigh, Brillouin and Raman scattering, etc.^1-7,21 These applications are based on dynamic (transient) gratings, generated by periodic modulations of the sample optical properties as result of different excitations, that ultimately drive the time evolution of the created gratings. Hence, the capability to generate, control and probe the time dependence of EUV transient gratings at ultrafast timescales is an essential step towards the development of FWM at sub-optical wavelengths. Though the potential high impact of using short wavelength photons has been discussed in a number of theoretical and perspective works^7-10,12,21 and evidences for basic EUV/x-ray non-linear processes have been reported,^22-25 the experimental investigations of FWM in this spectral range were prevented by the lack of fully coherent sources with high brilliance. In this letter we report the experimental evidence of FWM processes stimulated by EUV transient gratings, generated by two coherent EUV pulses provided by the FERMI FEL.¹⁵

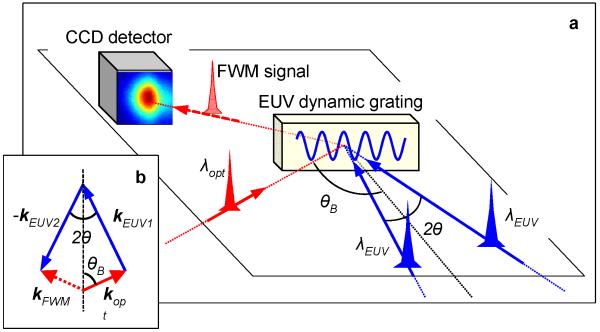
Fig. 1a shows a sketch of the experiment: two FEL pulses (wavelength λ_EUV=27.6 nm, estimated time duration 60-80 fs, pulse energy I_EUV1≈I_EUV2≈5 μJ, spot size ≈0.04 mm²) are crossed (angle: 2θ=6.16°) on a vitreous SiO₂ sample with the surface oriented orthogonally to the bisector of the FEL beams. The interference of the two pulses generates EUV transient gratings (TG) with a spatial periodicity L=λ_EUV/2sin(θ)≈256.8 nm. An optical pulse (λ_opt=392.8 nm, time duration ≈100 fs, pulse energy I_opt≈2 μJ, spot size ≈0.002 mm²), coplanar to the FEL beams, was sent into the sample at an angle of incidence θ_B=49.8°. The polarization of the fields was orthogonal to the scattering plane. The chosen (λ_EUV,λ_opt,2θ,θ_B)-values fulfill the phase matching condition (see Fig. 1b), which in the present TG experiment reduces to: λ_EUVsin(θ_B)=λ_optsin(θ). This determines the propagation direction of the FWM signal: k_FWM=k_EUV1-k_EUV2+k_opt, where k_EUV1,2 and k_opt are the wavevectors of the EUV fields and of the optical one, respectively. Along k_FWM the non-linear signal, radiated by different portions of the sample, adds coherently, yielding to a FWM signal propagating downstream the sample as a well-defined beam.^1-7,21 The experiment was carried out at the DiProI end-station using a purposely designed experimental setup based on reflective optics (see Methods for details). Such a setup lets us to adjust 2θ, θ_B, the time delay between the crossed FEL pulses (Δt_EUV-EUV) and those between the FEL pulses and the optical one (Δt). FEL-pump/optical-probe transient reflectivity measurements were used to determine Δt_EUV-EUV=0 and to equalize the fluence of the two FEL pulses in the interaction region. The FWM signal was detected by a CCD placed along k_FWM. After illumination by about 100’s FEL shots, creation of permanent gratings was observed at FEL fluences larger than ≈50 mJ/cm² per pulse (see Methods for details). The illumination of these permanent gratings by the optical laser led to a diffracted signal along k_FWM even in the absence of the FEL pulses. During the FWM measurements the FEL fluence was kept below 50 mJ/cm² in order to avoid the creation of permanent gratings.

Figure 1. FWM experiments with EUV transient gratings.

a, sketch of the FEL-based FWM experiment: 2θ=6.16°, θ_B=49.9°, λ_EUV=27.6 nm and λ_opt=392.8 nm are the crossing angle between the two FEL beams that generate the EUV dynamic grating, the angle between their bisector (dashed black line) and the optical beam, the FEL and laser wavelength, respectively. A CCD sensor is placed along the expected propagation direction of the FWM signal beam (k_FWM), which is determined by the “phase matching” (shown in (b); here k_opt, k_EUV1 and k_EUV2 are the wavevectors of the optical and of the two FEL pulses, respectively).

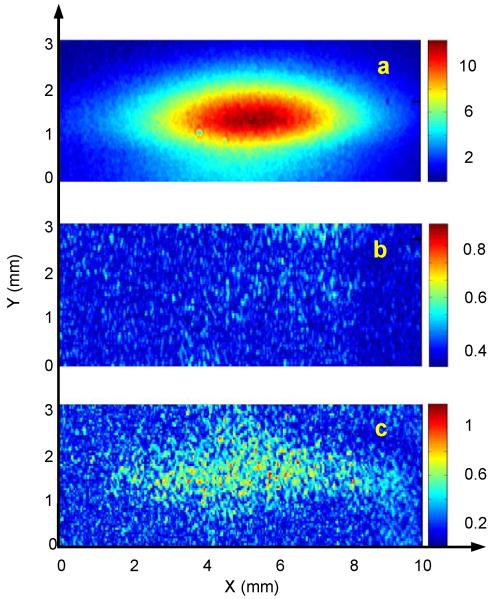
Fig. 2a shows a CCD image of the FWM signal beam acquired at Δt=0, whereas Figs. 2b and 2c report the same measurement for Δt=−0.5 ps and 70 ps, respectively. The observation of a signal that propagates along k_FWM for Δt>0 in the concurrent presence of the three input beams undoubtedly demonstrates the occurrence of FWM processes stimulated by EUV transient gratings. The large angular spread observed along the plane of the input beams can be attributed to relaxed phase matching conditions, likely due to the fact that both L and the EUV absorption length (L_EUV≈30 nm) are shorter than λ_opt. The total intensity of the FWM signal (I_FWM) at Δt=0 was ≈6·10⁵ photons/shot, corresponding to an efficiency η_FWM=I_FWM/I_opt≈1.5·10⁻⁷. Concerning magnitude justifications, the strength of the FWM field radiated by the sample (E_FWM) is related to those of the input fields as E_FWM~χ⁽³⁾E_EUV1E_EUV2E_opt ^1-3,5-7. In the present case we estimated E_EUV1≈E_EUV2≈0.8·10⁹ V/m, so that an effective value for the 3^rd order susceptibility |χ^(3)*|≈(η_FWM)^1/2/(E_EUV1E_EUV2)≈6·10⁻²² m²/V² (at Δt=0) can be estimated. This value is within the expected order of magnitude, since |χ⁽ⁿ⁾| scales as E_a^1-n, where E_a≈e/(4πε₀a₀²)≈5·10¹¹ V/m is the atomic field strength (here e, ε₀ and a₀ are the elementary charge, the dielectric constant and the Bohr radius, respectively).^2,5,6,26

Figure 2. FWM signal stimulated by EUV transient gratings.

Images from the CCD placed along k_FMW (X and Y are the directions parallel and orthogonal to the scattering plane, respectively). The images were acquired at Δt=0 (a), Δt=−0.5 ps (b) and Δt=70 ps (c), respectively.

The time evolution of η_FWM is shown in Fig. 3a. The data are scaled by the factor α=I_EUV1(Δt=0)I_EUV2(Δt=0)/[I_EUV1(Δt)I_EUV2(Δt)]. Approaching Δt=0 from negative delays a fast rise of the FWM signal, compatible with a cross-correlation profile (R_cc(Δt)), was detected. For Δt>0 an appreciable FWM signal is observed over the whole probed Δt-range (i.e. up to 130 ps). The signal observed at large Δt’s (>10 ps) can be ascribed to thermal relaxations and longitudinal acoustic modes.³ The latter is expected to induce a signal modulation at frequency ν_LA=c_s/L≈23.2 GHz (where c_s=5970 m/s is the sound velocity of vitreous SiO₂), which is compatible with our data. Fig. 3b displays the FWM signal in the 0-1.6 ps range after R_cc(Δt) is subtracted. Here the time structure of the FWM signal is compatible with two oscillations at frequencies ν₁≈1.15 THz and ν₂≈4.1 THz. The latter frequency roughly matches that of the ν_2b Raman modes, due to tetrahedral bendings, while the former, that accounts for the leading modulation of the observed FWM signal, can be ascribed to F₁ hyper-Raman modes, that involve rotations of SiO₄ tetrahedra (see Methods for details).

Figure 3. Time evolution of the FWM signal.

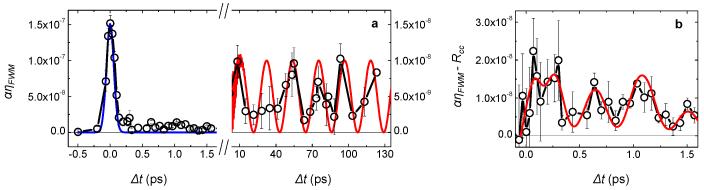
a, black circles connected by lines are the time dependence of the FWM signal, scaled to the intensity of the input beams (error bars are estimated as one standard deviation of the set of CCD images corresponding to the same Δt value); the blue and red lines are R_cc and the expected signal modulation due to acoustic modes, respectively. b, black circles connected by lines is the FWM signal after R_cc is subtracted. The red line is the modulation due to oscillations at frequencies ν₁=1.15 THz and ν₂=4.1 THz.

Our results demonstrate the generation of dynamic EUV gratings using fully coherent FEL pulses. The non-linear interactions between the induced grating and an optical pulse allowed us to observe the first FEL-stimulated FWM signal, that encodes the dynamics of impulsively stimulated collective vibrational modes with wavevector k_ex=|k_EUV1-k_EUV2|.³ This suggests how EUV transient gratings can drive coherent excitations into the sample and pave the way for the practical exploitation of non-linear optics in the EUV/SXR range. In this context, the next step that we will illustrate in the near future is to replace the optical pulse with an EUV/SXR one (EUV probing of optically stimulated transient gratings was already reported^27,28) to probe vibrational modes in the 0.1-1 nm⁻¹ k_ex-range.²¹ This range, inaccessible by optical FWM (see Fig. 4a), can be probed by using photon wavelengths down to 10 nm (i.e. well within the range of FERMI),²¹ and is of special relevance for the investigations of disordered systems. Indeed, the origin of their thermodynamic peculiarities (e.g. the highly debated excess specific heat) seems to be related to “mesoscopic” heterogeneities extended over a few nm lengthscales, which can be revealed by the anomalous behavior of vibrational modes in the 0.1-1 nm⁻¹ k_ex-range.^29,30

Figure 4. Outlooks.

a, energy-wavevector (ω_ex-k_ex) range of typical excitations in condensed matter and corresponding time-length scales. The green area sketches the range accessible by optical FWM while the double-ended blue vertical arrow is the range probed in the present work; the horizontal dashed line is the time duration of the excitation pulses. The area delimited by the thick blue lines represents the (ω_ex-k_ex) range accessible by EUV/SXR FWM, with the addition of a EUV/SXR probe and the development of EUV/SXR CRS. b, wavevector arrangement for a CRS process involving two-colours FEL excitation pulses (|k_EUV1|≠|k_EUV2|); k₃ and k_FWM are the wavevectors of the probe and signal beams, respectively. c, level scheme in case ω_EUV1 is tuned to the energy of a core state (CS) transition and ω_EUV1-ω_EUV2 to a lower energy excitation (ω_ex). GS and ES are the ground and excited states, respectively, while VS is a virtual state (in standard CRS the CS is replaced by a VS); τ is the eventual time delay between the two excitation pulses while ω₃ and ω_FWM=ω₃+ω_ex are the photon energies of the probe and signal beams, respectively. d, the independent control of three EUV/SXR input beams might allow to separately tune the energy of the excitation and probe beams to CS’s of two distinct atoms (atom-A and atom-B), hence allowing for monitoring the excitation dynamics among two different atomic sites^6,7 (a valence band exciton in this sketch;⁷ here VB and CB are the valence and conduction bands, respectively).

An opportunity offered by the FEL technology is the use of two-colour FEL pulses^16-19 to generate coherent populations of excited states via FWM processes, such as coherent Raman scattering (CRS).^2,4-7 In CRS the excitation energy and wavevector are set by the photon energy difference (ω_ex=ω₁-ω₂) of the stimulating pulses and by the grating vector k_ex=k₁-k₂, respectively (see Figs. 4b and 4c). Compared to the optical regime, EUV/SXR pulses (10-1000 eV) will allow to coherently stimulate excitations at higher energy (e.g. excitons with ω_ex=1-10 eV).^5-7 These can be probed by a third pulse, generated by the FEL^5,6,20 or by an external source.^27,28 Furthermore, when the field frequencies of the stimulating and/or probing pulses are tuned to core resonances of given atoms, the localization of core shells turns into an atomic-scale localization of the site at which the selected excitation is created and/or probed (see Figs. 4c-4d). In a nutshell, by tuning the field frequencies and time delay it is possible to use FWM to gain real-time information on the excitation transfer between selected atomic sites. This possibility is forbidden in linear inelastic scattering where the light-matter interaction takes place at the same atomic site.⁷ Further-on multi-wave interactions allow the application of a time delay (τ, see Fig. 4c) between the excitation pulses (e.g. by setting Δt_EUV-EUV=τ≠0 in our setup). This is a substantial step towards multi-dimensional spectroscopy⁴ and may consent to distinguish resonant and non-resonant FWM signals. On experimental grounds the core-resonant FWM is still an unexplored field, though solid theoretical approaches and numerical studies in the SXR are available.^7,11 Core resonant FWM will soon be tested at FERMI, since many elements (C, Mg, Al, Si, Ti, etc.) have resonances within the photon energy range of FERMI (20-310 eV). The third harmonic of the FERMI FEL emission (photon energy range: 60-930 eV) and the forthcoming construction of self-seeded SXR FEL sources with a wider photon energy range (e.g. SCLS-II, SwissFEL and PAL-XFEL) could be most likely used to exploit resonances at higher energy.

FWM with elemental selectivity could have relevant applications,^6,7 for instance to study charge transfer dynamics in electrocatalytic processes occurring in photoelectrochemical cells, devices that mimic natural photosynthesis to convert sunlight into chemical energy (solar fuels). These are typically based on molecular complexes adsorbed on TiO₂ substrates and have a conduction/valence band dominated by the Ti/O orbitals. FWM with elemental selectivity may disentangle the timescales of electron and hole migration, by exploration of the Ti and O resonances, as well as to shed light on the water oxidation dynamics taking place at the catalyst by separating the signal originating from reaction centers.⁶ Since elements of biological interest (C, N, O) have resonances in the EUV/SXR range, applications in life sciences are also very likely.

The demonstration of FEL-based FWM represents a fundamental milestone towards the development of non-linear optics at sub-optical wavelengths. In this manuscript we demonstrate that EUV FWM is already possible by using fully coherent FEL pulses, as those routinely delivered by FERMI and, in the foreseeable future, by other EUV/SXR FEL facilities. The exploitation of this approach will allow to detect real-time correlations and charge/energy flows between different atoms, a capability unattainable by linear methods, as well as to probe the dynamics of elementary excitations (phonons, polarons, etc.) in an energy/wavevector range inaccessible by optical non-linear methods. These classes of non-linear experiments would become a powerful tool for revolutionary advances in physics, chemistry and biology.

Methods

Experimental setup

The FEL focusing was provided by a Kirkpatrick-Baez active focusing system (located upstream the DiProI end-station³¹), that was detuned to relax the spot size at the sample in order to avoid sample damage. The FEL photo-diagnostic data were acquired on a shot-to-shot basis by the Photon Analysis, Delivery and Reduction System (PADReS),³² that connects the FEL source to the end-station; an Al filter placed along the photon transport line was used to remove the seed laser radiation.

The layout of the experimental set up used to generate and probe EUV transient gratings is shown in Extended Data Fig. 1. The system to split and recombine the FEL beams (see Extended Data Fig. 1a) is based on three 70 mm long carbon-coated mirrors (M1, M2 and M3) working at grazing incidence. It is mounted on a 580×280 mm² baseplate and in the present case the grazing angles were ≈3°. M1 can be inserted into the path of the incoming FEL beam by a y-translation (see Extended Data Fig. 1a for the adopted reference frame) and is used as a wavefront division beamsplitter.^20,33,34 The two split beams propagating downstream M1 are recombined on the sample by mirrors M2 and M3. The design position of the mirrors corresponds to a parallelogram geometry, where the splitting angle after M1 (2α) equals the crossing angle at the sample (2θ) and the M1-M2 distance (d1) equals the M3-sample one (d2). In this case the optical path difference (ΔL) between the FEL path 1 (FP1) and FEL path 2 (FP2) vanishes, ensuring the time coincidence of the crossed FEL beams. The design values of the system are 2α=2θ=6° and d1=d2=125 mm. The system has several motorized degrees of freedom to adjust the mirror positions and angles during the experiment, i.e.: i) the pitch and roll angles of all mirrors can be independently controlled in the ±3.5° range with a resolution of ≈50 μrad by piezo-electric steering motors; ii) the y-position of M1 can be changed in the ±20 mm range with ≈2 μm resolution; iii) the x and y positions of M2 and M3 can be independently varied in the ±9.5 mm range by linear piezomotors with a resolution of ≈0.2 μm; iv) each mirror can be removed from the FEL paths; v) the whole system can be adjusted in x, y and z. Furthermore, the sample is mounted on a (x,y,z,pitch,roll) adjustment stage, that also allows to replace the SiO₂ sample with a fluorescence screen, a pinhole (PHsam) or a Si₃N₄ reference sample (for cross-correlation measurements described further below). Such motors can be used to change the value of 2θ (in the 3°-9° range) keeping fix the arrival time difference of the two FEL pulses (Δt_EUV-EUV) or vice-versa; see sketches in Extended Data Figs. 1d and 1e. The possibility to vary Δt_EUV-EUV (in the ±0.2 ps range for 2θ≈6°) at fixed 2θ de facto makes our setup a compact split and delay device, with the advantage of the angular discrimination of the two FEL pulses.

The system was pre-aligned using a Ti:sapphire laser to simulate the incoming FEL beam and optimizing the second harmonic signal generated by a non-linear crystal placed at the sample position (this signal is sensitive to the time-space superposition of the beams coming from FP1 and FP2). The optimized geometry was then referenced by a set of 2 mm diameter pinholes (PHin, PHout, PH1, PH2, PH3, PH4, PHsam) before plugging the set-up into the end-station; PHsam can be inserted in place of the sample, while PHsam and PHout can be independently scanned in y in order to determine both the parallelism and the interaxis distance (h) between the trajectory of the incoming FEL beam (once removed M2 from the scattering plane) and FP2 downstream M3. This set of pinholes provides an accuracy of about 0.2° in the determination of 2θ. Indeed, from atomic force microscopy measurements on permanent gratings (carried out after the experiment) we were able to determine the actual value of 2θ (i.e. 6.16°±0.02°) used in the FWM measurements. Such deviations with respect to the design value can be compensated by changing the FEL wavelength (λ_EUV)³⁵ and/or the incidence angle of the optical pulse at the sample (θ_B).

A sketch of the system (external to the end-station) used to control the optical pulse is shown in Extended Data Fig. 1b. This pulse is a fraction of the one that triggers the FEL emission, thus ensuring “jitter-free” conditions, i.e. the FEL-optical timing jitter (<10 fs)³⁶ is much shorter than the pulse duration. An optical delay line (DL) is used to set the time delay (Δt) between the FEL pulses and the optical one in the −10 +300 ps range. The optical beam is frequency doubled at 392.8 nm wavelength by a BBO (Barium Boron Oxide) crystal and routed into the sample by a reflective mirror (ML; grazing angle ≈22.5°) and a focusing lens (FL; focal length 600 mm), whose focal plane contains the crossing point of the two FEL beams. ML can be translated along the y-direction in order to change θ_B (in the 47°-51° range) without varying the position of the laser spot at the sample. This degree of freedom is coupled to Δt, so that a change in θ_B has to be compensated by an adjustment of the DL to keep fix the actual value of Δt. Bandpass filters (BFs) are used to remove the residual fundamental radiation at 785.6 nm wavelength, while a beamsplitter (BS) provides a reference beam for intensity monitor and active stabilization,³⁷ the latter is ensured by a tip-tilt stage action on the MLS mirror.

An accurate determination of the temporal and spatial coincidence of the three input beams is obtained by cross-correlation measurements.³⁸ These are based on FEL-induced transient optical reflectivity changes (ΔR/R) from a Si₃N₄ reference sample. In such measurements we first removed M3 from FP2 to collect the cross-correlation trace between the optical pulse and the FEL pulse coming from FP1. The half drop of the ΔR/R profile was assumed as Δt=0. Afterwards we removed M2 and inserted M3 in order to collect the cross-correlation trace associated to the FEL pulse coming from FP2. Iterative measurements, carried out by varying the pitch of M1 and roto-translating M3 keeping fix the FEL trajectory downstream M3 (see Extended Data Fig. 1e), allowed us to set the condition Δt_EUV-EUV=0. Furthermore, since the amplitude of the ΔR/R drop is proportional to the FEL fluence at the sample,^38,39 such measurements also allowed us to equalize the fluence level of the two FEL beams in the interaction region. Extended Data Figs. 1f and 1g report typical ΔR/R traces collected out/in time coincidence and without/with similar fluence levels in the interaction region. Once set the time-space coincidence of the three beams we acted on θ_B to optimize the phase matching conditions necessary to observe the FWM signal. The latter was recorded by a Princeton Instrument PI-MTE back illuminated Charged Coupled Device (CCD) camera with frame format 2048×2048 pixels and 13.5×13.5 μm² pixels size. The detector was positioned ≈250 mm downstream the sample and oriented at an angle of ≈49°. A 15×5 mm² slit was placed in front to the CCD in order to reduce spurious light, mainly coming from diffuse scattering of the optical pulse (transmitted through the sample) that impinged into the wall of the experimental chamber.

Atomic Force Microscopy (AFM) measurements on permanent gratings

Extended Data Figs. 2a, 2b and 2c show AFM topographies of a 8×8 μm² sample area not irradiated by the FEL pulses, irradiated by ≈300 shots at fluence larger than 50 mJ/cm² and continuously irradiated by FEL pulses at low fluence, respectively. AFM scans have been performed with a XE-100 (Park Instruments) instrument, in contact mode using commercial cantilevers (Mikromasch, CSC38, spring constant k=0.03-0.09 N/m) with samplings of 1024 pixels in both directions. Extended Data Figs. 2d-2f report the corresponding depth profiles of the sample surface. The non-irradiated sample shows a roughness of about 0.6 nm root-mean-square and 5 nm peak-to-valley. A grating with a peak-to-valley amplitude of about 18 nm and a period of 256.7±0.9 nm (corresponding to 2θ=6.16°±0.02°) is clearly visible in the sample surface irradiated at high FEL fluence. The high grating visibility after multi-shot illumination indicates that the shot-by-shot fluctuations in the optical path difference (i.e. in the relative phase) between the crossed FEL pulses are lower than λ_EUV. Such a low phase jitter might in principle allow for lithographic applications. Indeed, the interference between coherent FEL pulses would permit to imprint permanent gratings with a pitch as short as a few nm’s by exploiting larger crossing angles and shorter FEL wavelengths. Extended Data Figs. 2g-2i are the power spectral densities (PSD) of the data reported in Figs. 2d-2f. No specific frequencies are found in the non-irradiated sample (the peak at ≈35 μm⁻¹ is an artifact due to the electronic noise of the employed AFM device), while the first peak at ≈0.5 μm⁻¹ in the PSD, shown in Extended Data Fig. 2h, reveals a modulation with a period of ≈2 μm, most likely due to diffraction effects from the mirrors. The sample surface irradiated at low fluence shows a roughness similar to that of the non-irradiated sample and frequencies ascribable to the formation of permanent gratings are absent.

Data Analysis

For each probed Δt-value we acquired 5 CCD images (exposure time: 1 minute) with the FEL ON and 2 ones with the FEL OFF. The FEL OFF images were used to remove the background due to diffuse scattering of the optical laser, mainly due to the fraction of the laser pulse transmitted through the sample, which then impinged into the wall of the experimental chamber. Such frequent and accurate determination of the background allowed us to account for small drifts in the CCD response during the Δt-scan, which lasted several hours. After background subtraction we applied a low-pass Fourier filter in order to reduce the noise and improve the contrast. In order to convert the ADC counts, recorded by the CCD, into incoming photons we assumed a sensibility of 8.5 photons per ADC count, which also takes into account the detector quantum efficiency. The total number of photons in the FWM beam was determined by fitting the peak in each image with a 2-dimensional Gaussian function plus a flat background and then calculating the volume under the Gaussian surface. The volume corresponding to each image was then averaged taking into account the normalization to the corresponding mean squared FEL intensity; error bars were estimated as one standard deviation of the set of CCD images corresponding to the same Δt value (in a few cases we have a single image and we hence set the error bar equal to zero). At negative time delays (Δt<0) and within the signal-to-noise of the employed CCD detector, the “FEL ON – FEL OFF” images can be fitted only by the background (see also Extended Data Fig. 3). Before starting the time delay scan, shown in Fig. 3a, we optimized the FWM signal at Δt=0 by small tweaks of mirror positions and angles. The intensity stability of the FEL was typically better than 7 % during the acquisition of the 5 FEL ON images and of about 20 % throughout the whole Δt-scan. A few images were discarded due to occasional machine faults occurring during the acquisitions.

In a proof-of-principle spirit we assumed that the time dependence of the FWM signal is due to impulsively stimulated vibrational modes, which can be observed in the time-dependent coherent FWM signal.^3,40 We hence modeled the time dependent intensity of the normalized FWM signal (αI_FWM(Δt)/I_opt; where I_opt and α are the intensity of the incoming optical beam and the normalizing factor quoted in the main text, respectively) with the following function:

$$\frac{\alpha I_{FWM}\left(\Delta t\right)}{I_{opt}}=R\left(\Delta t\right)\otimes {\mid A_0\delta \left(\Delta t\right)+{\Sigma }_i{A}_i{e}^{-\Delta t∕{\tau }_i}\sin \left(2\pi {\nu }_i\Delta t\right)\mid }^2=A_0^{2}R\left(\Delta t\right)+R\left(\Delta t\right)\otimes {\mid {\Sigma }_i{A}_i{e}^{-\Delta t∕{\tau }_i}\sin \left(2\pi {\nu }_i\Delta t\right)\mid }^2,$$ (1)

where A₀ and A_i are scaling factors, ⊗ is the convolution operator, R(Δt) is the instrumental response function, while ν_i and τ_i are the frequencies and damping times of the impulsive stimulated modes, respectively. Since an independent determination of R(Δt) is not available, it was assumed to be a Gaussian function of unit area with a full width at half maximum of 135 fs, which is equal to that of the Δt=0 peak in the FWM signal (R_cc(Δt); see Fig. 3a). Hence, the A₀δ(Δt) term accounts for processes occurring at timescales substantially shorter than ≈100 fs. The e^−Δt/τ_i sin (2πν_iΔt terms describe the time evolution of the impulsively excited vibrational modes. Considering that the excitable modes are those having vibrational periods (ν_i⁻¹) longer than the time duration of the stimulating FEL pulses (60-80 fs),^3,40 the observed FWM signal could be related to: i) acoustic modes (ν_LA=c_s/L≈23.2 GHz, where c_s=5970 m/s and L=256.8 nm are the sound velocity and the transient grating pitch, respectively); ii) Raman modes within the broad band (3-14 THz) associated to tetrahedral bendings⁴¹ and iii) F₁ modes (≈1 THz) involving coupled rotations of SiO₄ tetrahedra.^42,43 Starting from such trial frequencies, we used Eq. 1 to optimize the parameters that better describe the time structure of the FWM signal, once subtracted the A₀²R(Δt) term. The coarse sampling and the limited Δt-range prevented the direct determination of acoustic parameters, that were fixed to the expected values, i.e.: ν_LA=23.2 GHz and τ_LA>1 ns (we note that in the probed Δt-range e^−Δt/τ_LA ≈ 1), while A_LA was fixed to 1·10⁻⁴ in order to fit in the observed magnitude of the FWM signal at Δt>2 ps. The optimized values of the other parameters are: A₁/A_LA=1.4±0.2, ν₁=1.15±0.15 THz, τ₁=5±2 ps, A₂/A_LA=1.4±0.2, ν₂=4.1±0.8 THz and τ₂=0.15±0.06 ps. The value of ν₁ roughly matches the characteristic frequency of F₁ modes,^42,43 while ν₂ locates in the low frequency side of the aforementioned broad Raman band, that corresponds to (highly damped) ν_2b bending modes.⁴¹ We finally notice that a slightly worse fit (but still satisfactory) is achieved without the A₂ term, while the addition of other high frequency terms (as the ν_4b,4c bendings)⁴¹ does not significantly improve the fitting results.

Extended Data

Extended Data Figure 1. Experimental setup for FEL-based FWM measurements.

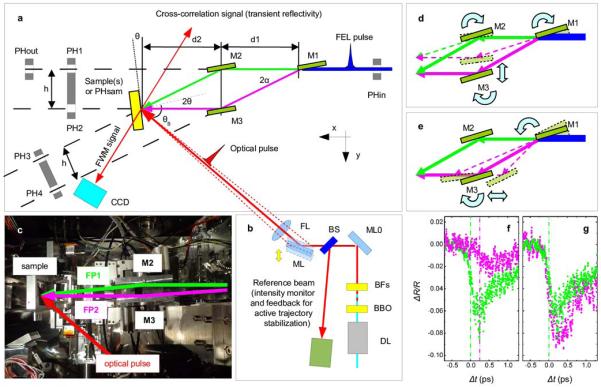
a, Top-view layout of the experimental set-up used to split and recombine the FEL beams. b, Top-view layout of the experimental set-up used to control the optical beam. c, Top-view picture of the set-up: the two FEL paths (FP1 and FP2) downstream M1 and the trajectory of the optical pulse are indicated. d, sketch of the movements needed to change 2θ keeping fix Δt_EUV-EUV. e, sketch of the movements needed to change Δt_EUV-EUV keeping fix 2θ. f and g, optical reflectivity changes in Si₃N₄ induced by the FEL beam propagating through FP1 (green dots) and FP2 (magenta dots). In (f) the mirrors were displaced with respect to the nominal position; a poor time coincidence and a different fluece level in the interaction region can be appreciated. g, same measurements as in (f) after optimization of the geometry; the superposition of the two traces indicates a large improvement in the time coincidence and a similar FEL fluence in the interaction region.

Extended Data Figure 2. AFM topographies.

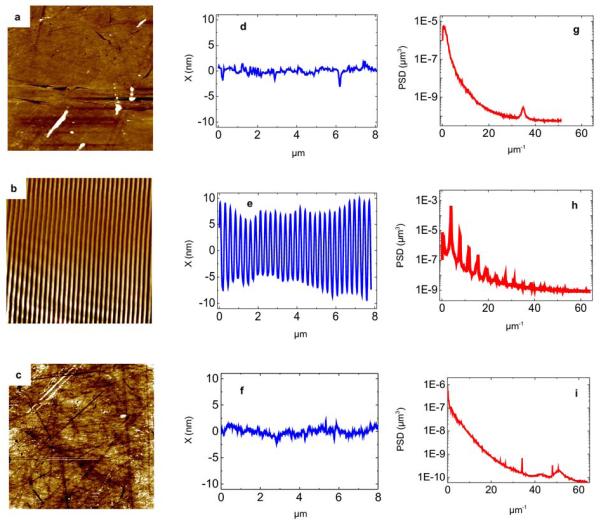
AFM topographies of 8×8 μm² areas of the sample surface in a not irradiated region of the sample (a), in an area irradiated by ≈300 FEL shots at fluence larger than 50 mJ/cm² (b) and in an area continuously irradiated by FEL pulses at low fluence (c). d-f are representative depth profiles of the sample surface along the green lines shown in panels a-c. The power spectral densities (PSD) corresponding to data reported in d-f are shown in g-i.

Extended Data Figure 3. Time sequence of acquired data.

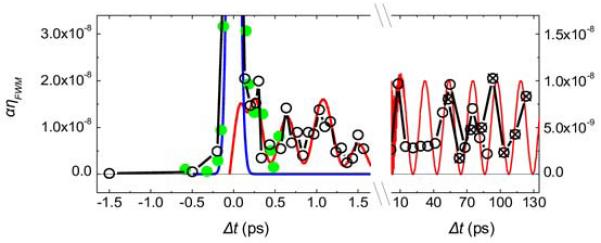
Black open and crossed circles connected by lines are data shown in Fig. 3; crossed circles correspond to a scan made several hours after the one corresponding to data shown as open circles, in both scans the time delay was continuously increased. Green dots are data collected before these two scans; here we had not yet optimized the FWM signal at Δt=0 (these data are scaled by a factor to fit the peak intensity of the data shown as black circles). Blue and red lines are the same shown in Fig. 3.