Estimating a structured covariance matrix from multi-lab measurements in high-throughput biology

Abstract

We consider the problem of quantifying the degree of coordination between transcription and translation, in yeast. Several studies have reported a surprising lack of coordination over the years, in organisms as different as yeast and human, using diverse technologies. However, a close look at this literature suggests that the lack of reported correlation may not reflect the biology of regulation. These reports do not control for between-study biases and structure in the measurement errors, ignore key aspects of how the data connect to the estimand, and systematically underestimate the correlation as a consequence. Here, we design a careful meta-analysis of 27 yeast data sets, supported by a multilevel model, full uncertainty quantification, a suite of sensitivity analyses and novel theory, to produce a more accurate estimate of the correlation between mRNA and protein levels—a proxy for coordination. From a statistical perspective, this problem motivates new theory on the impact of noise, model mis-specifications and non-ignorable missing data on estimates of the correlation between high dimensional responses. We find that the correlation between mRNA and protein levels is quite high under the studied conditions, in yeast, suggesting that post-transcriptional regulation plays a less prominent role than previously thought.

1 Introduction

We consider the problem of estimating the degree of coordination between transcription and translation, in yeast. A credible estimate would have two important substantive implications. It would help assess the extent to which analyses that take measures of transcription as proxies for measures of translation, are valid. A credible estimate would also help quantify the relative roles of transcriptional versus post-transcriptional regulation.

Several studies have addressed this problem over the years, in organisms as different as yeast and human, with diverse technologies (Gygi et al. 1999; Abruzzo et al. 2005; Castrillo et al. 2007; Ingolia et al. 2009; Vogel et al. 2010; Schwanhäusser et al. 2011). Typically, transcription is quantified in terms of the concentration of messenger RNA (mRNA), corresponding to different genes, while translation is quantified in terms of the ratio of protein abundance to mRNA. If rates of translation and degradation did not vary by gene, then protein-mRNA ratios would be constant, and mRNA-protein levels would be perfectly correlated (de Sousa Abreu et al. 2009). Accordingly, the correlation between the vectors of mRNA and protein concentrations has been used as a proxy for the degree of post-transcriptional regulation. Published estimates of the correlation are low, mostly between 0.3 and 0.6, and do not seem to increase with more modern technologies. Thus, the consensus is that the there is significant regulation of protein levels after transcription, especially in higher organisms and mammals. This finding is quite surprising. The community agrees the extent to which mRNA and protein levels correlate is still unclear (Vogel and Marcotte 2012).

A close look at this literature suggests that the lack of reported correlation is not surprising after all. These studies are not based on a careful design, nor they carry out statistical analyses carefully, and ignore key aspects of how the data connect to the estimand. For instance, analyses are often limited to complete cases, discarding mRNAs and proteins with missing measurements. They ignore that missing measurements are more likely to be taken on mRNAs and proteins that are rare in cell. Structure in the variability of measurements, often referred to as batch effects (Leek et al. 2010), is not accounted for. Arguably, the low reported correlations are more likely to be due to limitations in the designs and analyses, rather than to limitations in the technology, or to aspects of regulation.

Conceptually, we can decompose the correlation into contributing components that should inform an appropriate study design and analysis. Namely, the main components that contribute to variation in the observed correlation between mRNA and protein levels are: differences in strain, technology and growth rate, the amount of alternative splicing, additional variability structured according to experiments, replicated measurements within an experiment, and actual biological variation (Raser and O'Shea 2005; Wallace et al. 2013).

Here, we design an original meta-analysis of 27 yeast data sets, supported by a multilevel model, full uncertainty quantification, a suite of sensitivity analyses and novel theory, to produce a more accurate estimate of the correlation between mRNA and protein levels. Briey, the proposed design controls for strain and reported growth rate, includes multiple technologies for measuring mRNA and protein levels. A simple multilevel model accounts for the structure in the meta variance-covariance matrix, and includes a non-ignorable missing data mechanism for missing measurements (Gelman and Hill 2006; Rubin 2004; Ibrahim et al. 2005). A limited amount of splicing in yeast (Parenteau et al. 2008) and other sources of variation contribute to the residual error. The strategy for the meta-analysis is to first fit a simple normal-normal multilevel model, in which technologies are assumed as exchangeable. While this model is theoretically identifiable in the absence of missing data, or in the presence of data missing completely at random, properties of the inference under under non-ignorable missing data are uncertain. We show empirically that inference achieves nominal frequentist coverage for a number of key parameters in the presence of non-ignorable missing data, using posterior predictive meta data, in Section 4.1, and that the model is robust to departures from normality, in Section 4.2. In Section 4.3 we use this model to estimate the correlation between mRNA and protein levels. We then explore the impact of relaxing the exchangeable technologies assumption on the correlation estimates, in Section 4.4.

From a statistical perspective, this problem motivates new theory on the impact of noise, model mis-specifications and non-ignorable missing data on estimates of the correlation, in Section 3. These theoretical results are illustrated by the analysis presented in Section 4.2. It is worthwhile noting that, while standard theory exists that characterizes the impact of measurement noise and model mis-specifications on mean coefficients, and in some cases variance coefficients, there is no theory that characterizes the impact of such specifications on the covariance or correlation between high-dimensional responses, e.g., mRNA and protein concentrations, which is the estimand of interest in the problem we consider.

From a substantive perspective, we find that the correlation between mRNA and protein levels is quite high, in yeast, suggesting that post-translational regulation plays a less prominent role than previously thought.

1.1 Data collection and exploratory data analysis

We gathered 16 data sets that measure mRNA expression and 11 that measure protein concentrations, mostly published, yielding a total of 58 high-throughput measurements on 5,308 genes and their corresponding proteins in yeast. The measurements were taken on yeast cultures using different technologies including custom and commercial microarrays, high-throughput sequencing and mass spectrometry.

The goal of the analysis is to study the steady state correlation of mRNA and protein levels. Thus it is important to use data that were collected under similar experimental conditions; from haploid yeast S. cerevisiae growing exponentially in rich shaken liquid medium with 2% glucose between 22 and 30°C. Additional sources of variation are treated as noise for the purpose of the analysis.

Details of the data sets are summarized in Table 1. Throughout the paper we work with the natural logarithm of the raw data, as this is approximately normally distributed. This is standard in mRNA expression and protein abundance studies (Eisen et al. 1998).

Table 1.

List of mRNA data sets (above the midline) and protein concentration data sets (below the midline). If the data set has multiple measurements, the number of replicates in each data set is given after the technology name, in parentheses. ‘2D gel’ stands for two-dimensional gel electrophoresis, and ‘MS’ for mass-spectrometry. The last column is the missingness rate out of the 5,308 genes in our data set.

ID	Reference	Technology (measurements)	Missing
CAUS	Causton et al. (2001)	commercial microarray (×5)	19–22%
DUD	Dudley et al. (2002)	custom microarray (×4)	5%
GARC	García-Martínez et al. (2004)	custom microarray	1%
HOLS	Holstege et al. (1998)	commercial microarray	12%
ING1	Ingolia et al. (2009)	RNA-Seq (mRNA rich) (×2)	9–10%
ING2	Ingolia lab, unpublished, 2010	RNA-Seq (rq) (×2)	4–5%
ING3	Ingolia lab, unpublished, 2010	RNA-Seq (ca) (×2)	6–8%
LIP1	Lipson et al. (2009)	RNA-Seq (×6)	1%
LIP2	Lipson et al. (2009)	commercial microarray	4%
MAC	MacKay et al. (2004)	custom microarray	28%
MIUR	Miura et al. (2008)	cPCR (×4)	26–29%
NGAL	Nagalakshmi et al. (2008)	RNA-Seq	22%
PELE	Pelechano and Pérez-Ortín (2010)	custom microarray	14%
ROTH	Roth et al. (1998)	commercial microarray (×2)	59–70%
VELC	Velculescu et al. (1997)	SAGE	58%
YASS	Yassour et al. (2009)	RNA-Seq (×4)	5%
FUTR	Futcher et al. (1999)	2D gel	99%
GHAM	Ghaemmaghami et al. (2003)	Western blot	34%
GODO	de Godoy et al. (2008)	LC MS/MS	25%
GYGI	Gygi et al. (1999)	2D gel	98%
LEE	Lee et al. (2011)	LC MS/MS (×3)	67–76%
LU	Lu et al. (2007)	LC MS/MS	83%
NGAR	Nagaraj et al. (2012)	LC MS/MS (×6)	31%
NEWM	Newman et al. (2006)	GFP	60%
PENG	Peng et al. (2003)	LC MS/MS	74%
THAK	Thakur et al. (2011)	LC MS/MS (×3)	84–85%
WASH	Washburn et al. (2001)	LC MS/MS	77%

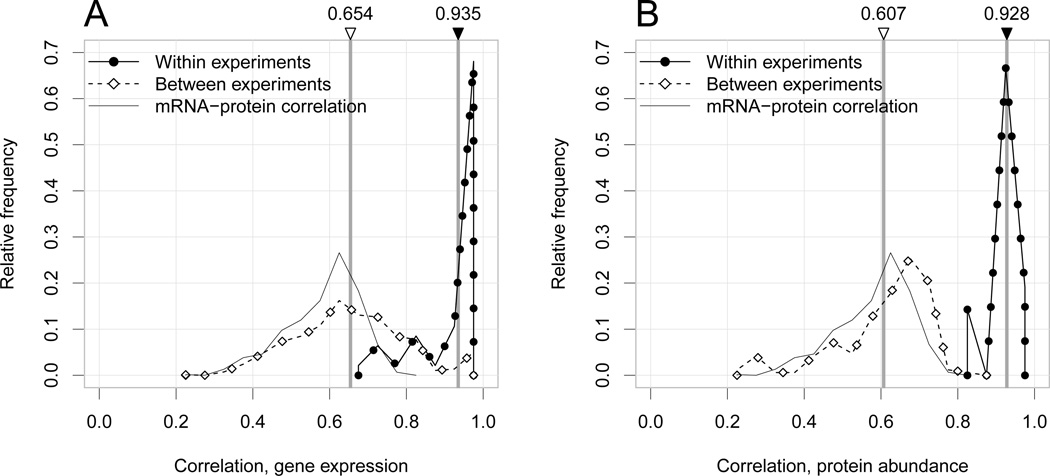
The data sets in Table 1 have features that, if unaccounted for, are likely to result in poor estimates of the correlation of interest. First, the measurements are inherently noisy. Both biological and technical noise attenuate correlation estimates; we define attenuation as bias towards zero. Second, the measurements are structured. We refer to an “experiment” to indicate a set of replicated measurements, whether technical or biological, which were obtained with a specific biotechnology and published in a specific paper (e.g., Ingolia et al. 2009; Lipson et al. 2009). The data we collected can be grouped according to biotechnology and experiment. As expected, the variability of the mRNA expression values is larger between experiments than between replicated measurements within an experiment (Figure 1). Interestingly, the range of the observed mRNA-protein correlations is almost the same as the between-experiment correlations, for both mRNA and protein levels. Principal component analysis of the replicates (see Figure 8 in the Appendix) confirms that experiment effects are large.

Figure 1.

mRNA expression data (left panel) and protein concentrations data (right panel) are highly structured. The plots show naive, biased Pearson correlation estimates between pairs of replicated measurements on the intersection of observed mRNAs/proteins; separately for replicates within experiments (solid) and across experiments (dashed). The thin black line in each panel shows the naive correlations between mRNA expression and protein replicates. The observed mRNA expression–protein correlations are comparable to the between-experiment correlations for both mRNA expression and protein levels. The top labels indicate the mean pairwise correlation between and within experiments.

Third, a considerable portion of the data in any given experiment is missing. On average, over 25% of the values are missing in any replicated measurement, for either mRNAs or proteins, with some experiments missing over 95% of the values. The data sets with a very large number of measurements missing may be of questionable value for estimating the mRNA-protein correlation but they are included for completeness. These are classic data sets that originally led to the conclusion that mRNA and protein levels correlated poorly, and so their inclusion is natural.

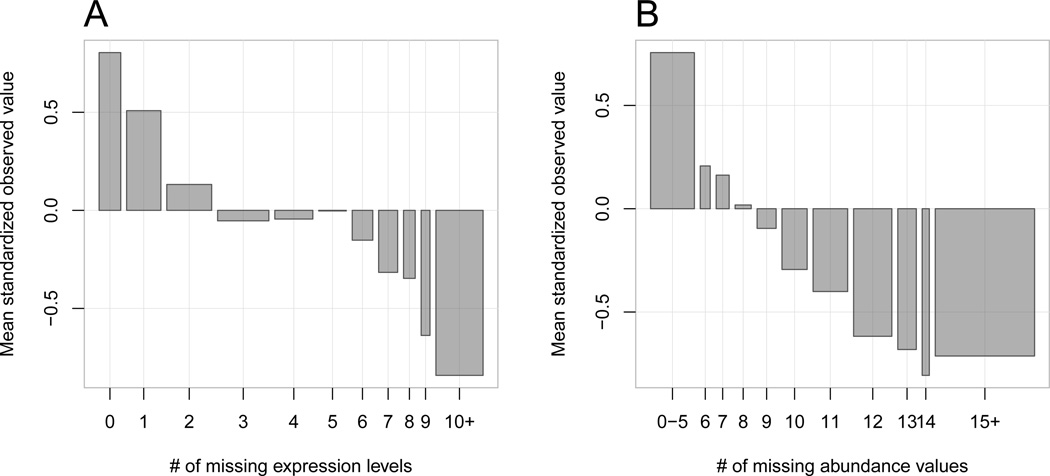
Notably, it is harder to obtain mRNA expression and protein concentration values for mRNA transcripts and proteins that are rare in the cell. A quick analysis of replicated measurements suggests that the fraction of missing values appears to be inversely related to the average observed values of both mRNA and protein concentrations. This analysis is illustrated in Figure 2 and in Table 7 in the Appendix.

Figure 2.

Unavailable values are not missing at random. The bars show the average observed mRNA levels (left panel) and protein concentration values (right panel), standardized, plotted as a function of the number of missing values for each mRNA (out of 38 total), or protein (out of 20 total). Bar widths are proportional to the number of genes (proteins) in each bin.

We give some theoretical insights in Section 3 on how each of these three effects attenuate the observed correlation, and also perform an analysis of simulated data in Section 4.2.

1.2 Contributions of this work

We estimate the degree of coordination between transcription and translation, in yeast. To accomplish that, we have curated a collection of 27 yeast data sets about mRNA and protein levels, in Table 1. We developed an original meta analysis strategy to estimate the amount of coordination, which we quantify in terms correlation between latent de-noised representations of mRNA and protein levels. This correlation is a parameter in a simple multilevel model that accounts for measurement error structure due to experimental protocols, replicated measurements, and technology biases (Johnson et al. 2007; Kipnis 2003). The analysis involves Bayesian confidence intervals, a suite of sensitivity analyses including an evaluation of frequentist coverage, robustness of the estimates to departure from key assumptions, such as normality and correct specifications of the covariance structure, and the effects of technological bias on the estimates. We also develop novel theory that provides analytical insights into the results of the sensitivity analyses we perform. Namely, we quantify the expected reduction in correlation as a function of (1) noise in the data; (2) experiment effects and model misspecification; and (3) non-ignorable missing data. This theory extends Spearman’s correction for the attenuation of correlation (Spearman 1904) between two quantities to a multivariate setting while accounting for experiment effects. In particular, while corrections for the effect of missing data on exploratory analyses have been explored (Wiberg and Sundström 2009), we are the first, to our knowledge, to discuss the estimation of correlation from multiple measurements each with different non-ignorable missing data mechanisms.

2 Methods

We posit a simple model to estimate a covariance matrix between high-dimensional responses, in the presence of structured measurement errors and non-ignorable missing data, and we develop a Markov chain Monte Carlo algorithm to perform inference. Models of this sort are well established in statistical applications (e.g., see Rubin and Little 2002; Johnson et al. 2007). We chose a combination of simple specifications to be able to develop novel theory for the estimated correlations, in Section 3. In Section 4.3, this model is used to carry out an original meta-analysis of the experiments listed in Table 1.

2.1 A structured covariance model of high-dimensional responses

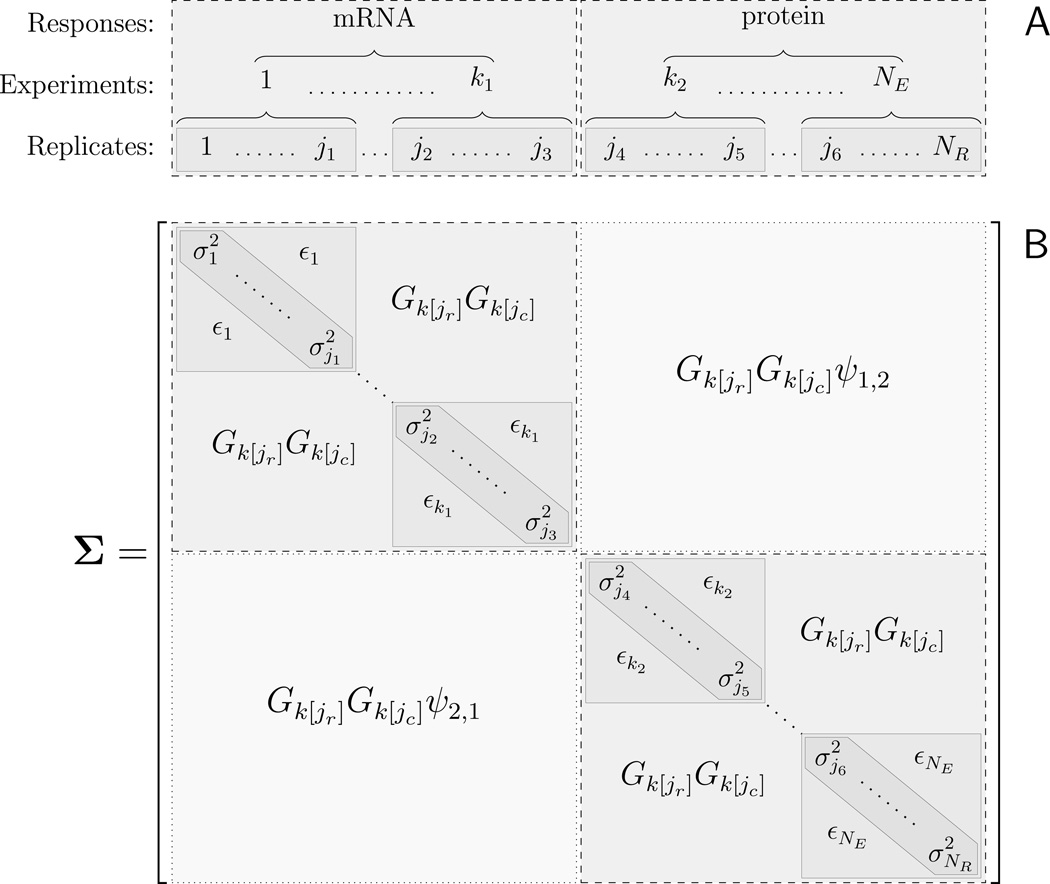
While the model we detail below is generally applicable for the estimation of a covariance matrix among multiple responses, we specify the data generating process for our goal of estimating the amount of coordination between mRNA transcription and protein translation. In this application, we consider two high-dimensional responses, with approximately 5,300 dimensions, corresponding to mRNA expression and protein abundance in yeast. Each response is measured multiple times in a number of experiments, where each experiment consists of one or more replicates. Let X_i,j denote the measurement for mRNA/protein i in replicate j. Replicates, experiments and response variables form a three-layer hierarchy of nested groups. Specifically, we have N_L latent variables at the top of the hierarchy (two in this paper, representing mRNA and abundance), N_E experiments measuring one of the latent quantities, and N_R total replicates across experiments. To write down the model, we define two functions that map replicates to the other two layers. The function l[j] maps a replicate to the response type (mRNA expression or protein abundance) and the function k[j] maps replicates to experiments. These mappings are such that k[j₁] = k[j₂] implies l[j₁] = l[j₂]; that is, replicates of the same experiment measure the same response.

The model has two components: an observation model p(I_i,j|X_i,j), which provides the probability of observing a value for mRNA/protein i in replicate j, given the latent mRNA/protein level, and a hierarchical model p(X_i,j|…) for the latent mRNA/protein levels themselves. We posit

$$X_{i,j}=L_{i,l[j]}{G}_{k[j]}+E_{i,k[j]}+R_{i,j}+{\nu }_j$$ (1)

$${\mathbf{L}}_i~{𝒩}_{N_L}(0,\mathbf{\Psi })$$ (2)

$$E_{i,k}~𝒩(0,{\xi }_k)$$ (3)

$$R_{i,j}~𝒩(0,{\theta }_j)$$ (4)

$$p(I_{i,j}=0|X_{i,j}=x)=\frac{1}{1+\text{exp}(-{\eta }_{k[j]}^0-{\eta }_{k[j]}^1{X}_{i,j})}$$ (5)

where the random variables L_i,l specifies the latent mRNA expression and abundance, for mRNA and protein i = 1, …, N, and L_i = [L_i,1, …, L_i,NL]′. The random variables E_i,k capture experiment effects for experiment k = 1, …, N_E, and R_i,j are measurement noise for replicate j = 1, …, N_R. Effects between experiments are independent, Cov(E_i1,k1, E_i2,k2) = 0 if k₁ ≠ k₂. Measurement noise is independent between replicates, Cov(R_i1,j1, R_i2,j2) = 0 if j₁ ≠ j₂. The parameter ν_j reflects replicate specific bias common to all mRNAs/proteins. The coefficient G_k is an experiment specific scaling factor for the latent expression and abundance. The indicator variable I_i,j denotes whether the value for X_i,j was observed and accounts for non-ignorable missing data as detailed in Section 2.1.2.

The estimand of interest, Ψ, specifies the correlation matrix of the response variables. For our application, N_L = 2 and ψ_1,2 represents the correlation between the true mRNA and protein levels. The diagonal of Ψ is fixed to one for identifiability. The parameters ξ_k and θ_j specify the variances of the effects for experiment k, and the measurement noise for replicate j, respectively.

To write down the likelihood, let X_i = [X_i,1, …, X_i,NR]′ denote all measurements (both observed and missing) across replicates for mRNA/protein i, and let X = [X₁, …, X_N] denote the N × N_R complete data matrix of all measurements. Then, X ~ 𝒩 (ν, I ⊗ Σ). Here the column covariance, Σ corresponds to the between experiment covariance. Since we assume independence between genes (but see Section 4.2), the row covariance is simply the N × N identity matrix.

Similarly, define I as the binary observation matrix of dimension N × N_R, and define the vectors ${\mathit{\eta }}^0=[{\eta }_1^0,\dots ,{\eta }_{N_E}^0],{\mathit{\eta }}^1=[{\eta }_1^1,\dots ,{\eta }_{N_E}^1]$, and ν = [ν₁, …, ν_NR]. Then the complete data likelihood for the proposed model is

$$ℒ(\mathbf{X},\mathbf{I}|\mathbf{\Sigma },{\mathit{\eta }}^0,{\mathit{\eta }}^1,\mathit{\nu })\propto \prod _{i=1}^N[{|\mathbf{\Sigma }|}^{-1/2}\text{exp}(-\frac{1}{2}({\mathbf{X}}_i-\mathit{\nu })\prime {\mathbf{\Sigma }}^{-1}({\mathbf{X}}_i-\mathit{\nu }))]\times ℒ(\mathbf{I}|\mathbf{X},{\mathit{\eta }}^0,{\mathit{\eta }}^1),$$ (6)

where

$$ℒ(\mathbf{I}|\mathbf{X},{\mathit{\eta }}^0,{\mathit{\eta }}^1)=\prod _{i=1}^N\prod _{j=1}^{N_R}{\left(\frac{1}{1+\text{exp}(-{\eta }_{k[j]}^0-{\eta }_{k[j]}^1{X}_{i,j})}\right)}^{I_{i,j}}{\left(\frac{\text{exp}(-{\eta }_{k[j]}^0-{\eta }_{k[j]}^1{X}_{i,j})}{1+\text{exp}(-{\eta }_{k[j]}^0-{\eta }_{k[j]}^1{X}_{i,j})}\right)}^{1-I_{i,j}},$$ (7)

and where Σ is a structured covariance matrix of size N_R × N_R detailed in Section 2.1.1.

Note that Table 1 lists a few experiments that contain only one replicate. For these experiments we simplify Equation 1 by removing the random effect for the replicate, R_i,j. This ensures that all the quantities remain identifiable.

2.1.1 Covariance structure

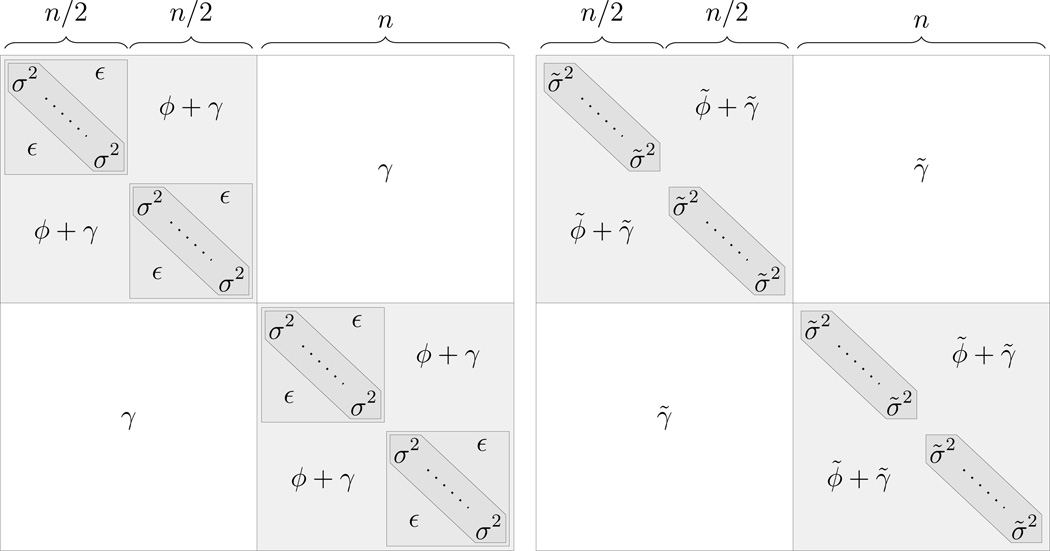
The nested response-experiment-replicate grouping leads to a structured covariance matrix, Cov X = Σ, for the complete data. Assuming that replicates are ordered according to response type and experiment (l[j] and k[j]) in X, Σ consists of N_L large blocks corresponding to the response variables; and each large block is a block diagonal plus rank one matrix, with one block for each experiment. Covariance matrices with this structure, illustrated in Figure 3, are often referred to as “similarity matrices” (e.g., see McCullagh 2006). In our model, Σ is a function of Ψ, ξ_k, θ_j and G_k. The marginal variance of each observation is

$${\sigma }_{i,j}^2=G_{k[j]}^2+{\xi }_{k[j]}+{\theta }_j.$$ (8)

Two replicates j₁ and j₂ within the same experiment k = k[j₁] = k[j₂] also have l = l[j₁] = l[j₂] and their covariance is $G_k^2+{\xi }_k$. The replicates are exchangeable within experiments but not between experiments.

Figure 3.

A) Responses, experiments and replicates form a nested group structure. B) These groups define a “similarity matrix”, a covariance matrix characterized by a block structure for Var X = Σ. The ${\sigma }_j^2$ marginal variances are given by Equation 8, ${\epsilon }_k=G_k^2+{\xi }_k$ is the within experiment covariance. G_k[jr] is the scaling factor for the experiment of the replicate corresponding to row j_r of the matrix, G_k[jc] is the same for column j_c.

2.1.2 Observation model

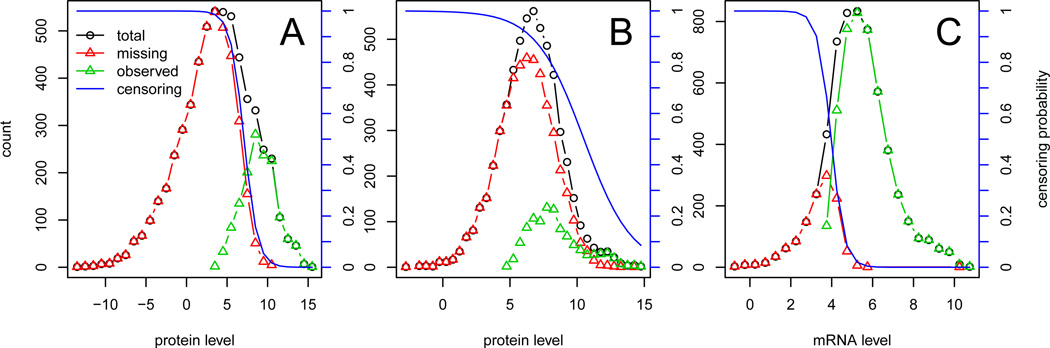
Figure 2 suggests that the fraction of missing data is negatively correlated with the average observed values for both mRNA expression and protein concentrations. This is evidence that the measurements are missing not at random (MNAR) (Rubin 2004).

We follow a well established approach to model this type of missing data mechanism, by means of a generalized linear model (Ibrahim et al. 2005). Equation 5 models the probability that measurement X_i,j is missing, p(I_i,j = 0), as a logistic function of the value of the measurement. The parameters of the missing data mechanism, ${\eta }_k^0$ and ${\eta }_k^1$, are shared by replicates within an experiment; they uniquely determine the probability that measurements are observed, conditional on X_i,j.

This observation model is flexible enough to include sharp censoring at a certain mRNA/protein value or to capture very little or no dependence of missingness on mRNA/protein levels. Importantly, the observation model parameters vary by experiments. See Figure 7 in the Appendix for some examples on how the observation model fits to various experiments.

2.1.3 Prior specifications

To complete the model specifications we place priors on Ψ, ξ_k, θ_j, ${\eta }_k^0$ and ${\eta }_k^1$. Recall that referenced works report correlation in the 0.3–0.6 range. In developing an independent meta-analysis, we use either at, or weakly informative, to produce estimates that are unaffected by previous results that arguably depend on problematic assumptions and methods. For the parameters ${\eta }_k^0$ and ${\eta }_k^1$ of the logistic observation model we use a Cauchy prior with mean zero and scale 2.5, after scaling the data (at each imputation step) to have mean zero and standard deviation 1/2, as suggested by Gelman et al. (2008). We assume at priors on the scaling factors, G_k, and the measurement bias parameters ν_j. For the replicate and experiment variances θ_j and ξ_k we use independent conjugate scaled inverse χ² priors with 3 degrees of freedom and scale 1/5. This is equivalent to an Inv-Gamma(3/2, 3/10) prior.

Since the primary estimand of interest is the correlation matrix Ψ, the choice of prior is particularly important. One option is to use the inverse Wishart prior, scaled to have unit variance. The inverse Wishart prior is the standard conjugative prior for covariance matrices, but it is quite restrictive. For instance, the inverse Wishart specifies the same degrees of freedom for every entry in the matrix. Crucially, with the inverse Wishart prior higher variances are associated with higher correlations.

As such, using a scaled inverse Wishart distribution to specify a prior actually corresponds to an informative prior on the correlations. To avoid this, we assume that the correlation and variance are independent. This is consistent with the separation strategy introduced by Barnard et al. (2000). This strategy involves putting a at prior (Unif[−1, 1]) on the correlation in the proposed model. The coverage studies of Section 4.1 indicate that the estimated correlation is not biased by this choice of prior.

2.2 Inference via Markov chain Monte Carlo

We fit the hierarchical model and the observation model jointly using a Gibbs sampler. Algorithm 1 provides an overview of the sampling strategy. A more detailed description of the individual steps follows.

Algorithm 1: The Gibbs sampler

Step 1. Since L_i and X_i are multivariate normal, L_i conditional on the other parameters is also multivariate normal. Specifically,

$$({\mathbf{L}}_i|{\mathbf{X}}_i,G_k,{\xi }_k,{\theta }_j,{\nu }_j)~{𝒩}_{N_L}(\text{Cov}({\mathbf{X}}_i,{\mathbf{L}}_i){\mathbf{\Sigma }}^{-1}({\mathbf{X}}_i-\mathit{\nu }),\mathbf{\Psi }-\text{Cov}({\mathbf{X}}_i,{\mathbf{L}}_i){\mathbf{\Sigma }}^{-1}\text{Cov}({\mathbf{X}}_i,{\mathbf{L}}_i)\prime ),$$ (9)

and Cov (X_i, L_i) can be easily calculated from Equation 1 and the parameters G_k, ξ_k, θ_j.

Step 2. Given L_i, we then draw Ψ using a Metropolis-Hastings random walk sampler. To sample the correlation, we use a truncated normal proposal, centered on the current value. Barnard et al. (2000) suggest setting the variance of the proposal distribution to a value inversely proportional to the number of measurements; after tuning, we set it to 1/(10N). When sampling from a bivariate covariance matrix, the truncation points for the proposal are simply −1 and +1, and the general formula is given by Barnard et al. (2000).

Step 3. The random effects and the variance parameters are drawn using Bayesian linear regression. First, for each experiment k, we draw G_k, ξ_k and E_i,k. Notice that X_i,j − R_i,j − ν_j is the same for all j replicates that belong to the same experiment k. So, we regress X_i,j − R_i,j − ν_j on L_i,l[j]G_k[j] for an arbitrary j for which k[j] = k holds and for all i ∈ 1, …, N. For the conjugate scaled Inv-χ² prior the posterior of ξ_k is also scaled Inv-χ². G_k is drawn from a normal, see Gelman et al. (2003, Sec. 14.2) for details. E_i,k correspond to the residuals of this regression.

Step 4. Similarly, we draw ν_j, θ_j and R_i,j for each replicate j, by regressing X_i,j on L_i,l[j]G_k[j] + E_i,k[j], i ∈ 1, …, N. ν_j are drawn from a normal, θ_j are drawn from a scaled Inv-χ², and the residuals of the regression correspond to R_i,j. Again, this is according to the textbooks, see Gelman et al. (2003, Sec. 14.2).

Step 5. Given these parameters, we impute the missing data. The conditional density for a missing measurement, i, in replicate j and experiment k[j] is proportional to the product of the logistic CDF and a normal density. That is:

$$p(X_{i,j}^{\text{missing}}|L_{i,l[j]},E_{i,k[j]},{\eta }_{k[j]}^0,{\eta }_{k[j]}^1,{\theta }_j)\propto \text{exp}(-\frac{{(X_{i,j}-(L_{i,l[j]}+E_{i,k[j]}+{\nu }_j))}^2}{2{\theta }_j})\frac{1}{1+\text{exp}(-{\eta }_{k[j]}^0-{\eta }_{k[j]}^1{X}_{i,j})}$$ (10)

While this density does not correspond to a simple conditional draw, it can be approximated by a normal. For low missingness probabilities, or censoring that occurs far out in the tails, the density is very nearly normal. For more extreme censoring, it is closer to the truncated normal density. Since we do not observe sharp missingness patterns, typically the observed data distribution is close to normal. We use a Metropolis-Hastings independence sampler with a normal proposal centered at the mode of the PDF and variance equal to the Hessian at the mode. We get over 90% acceptance using this approach.

Step 6. The parameters of the observation model are drawn from a normal, after Bayesian logistic regression on the missing and observed values to get the means and variances (Gelman et al. 2008).

3 Theory

In Section 2.1, we developed a simple high-dimensional random effects model for the latent measurement, with a missing data mechanism specified through a logistic regression. While standard theory exists that explores identifiability and the effects of noise, structured errors, and non-ignorable missing data on estimates of the regression coefficients of models of this sort (e.g., see Wang et al. 1996), to the best of our knowledge, no theory exists that explores the effects on estimates of the correlation. In this Section, we establish a few novel theoretical results in this directions. They provide insights into the results of Section 4.

We state mild conditions under which the parameters of our model are expected to be identifiable, in Section 3.1. We then demonstrate three ways in which an analysis that disregards key aspects of the data leads to attenuated estimates of the correlation, ψ_1,2. In Section 3.2 we specify, in the context of our model, the known result that noise attenuates correlation. In Section 3.3 we go further, proving that it is not enough to simply incorporate noise into the model– if we don't model the correlation structure of the noise between replicates, we still underestimate correlation. Finally, in Section 3.4 we state a condition under which ignoring missing data also coincides with negatively biased estimates of ψ_1,2. Below, we state and discuss the main results. The proofs are provided in the Appendix.

Ultimately, all three results suggest that any analysis which ignores measurement error, covariance structure, or missing data will typically understate the magnitude of linear dependence between the response variables. Since all of the biases are in the same direction, the errors do not cancel out. These results are consistent with the relatively moderate correlations reported in previous analyses, none of which account for these three features. As such, these theoretical insights further support our finding in Section 4.3 that the true correlation between mRNA expression and protein abundance is larger than previously reported.

3.1 Identifiability

Lee (2007, Sec. 2.2.2) states the conditions under which Gaussian random effects models (without missing data) are identifiable. For instance, a sufficient condition is that we fix diag (Ψ) = 1. According to this condition, the random effect portion of the model proposed in Section 2.1 is identifiable, up to a sign change, for all L_i,l[j] and G_k[j], since our model contains a single response variable for both mRNA expression and abundance levels.

The situation is more complicated for the observed data model because of the non-ignorable missing data mechanism. Simulation results in Section 4.1, obtained with parameters specified in Table 6, show near nominal frequentist coverage of the Bayesian posterior intervals obtained using our MCMC inference strategy. These empirical results suggest that identifiability is not an issue whenever measurements are missing according to Equation 5.

Table 6.

List of inferred posterior means for mRNA expression (above the midline) and protein concentration (below the midline) for every experiment. The total variance can be found using Equation 8. These parameter values are also used to generate the simulated data in Section 4.1 and 4.2. Refer to Table 1 for details about the individual data sets.

ID	${\eta }_k^0$	${\eta }_k^1$	Gk	ξk	θj
CAUS	−3.09	12.41	1.4	0.4	(0.09, 0.13, 0.58, 0.05, 0.03)
DUD	−3.96	−13.55	0.84	0.85	(0.53, 0.21, 0.29, 0.37)
GARC	−1.08	1.05	1.03	−	0.87
HOLS	−1.6	−3.92	1.46	−	0.27
ING1	−0.52	−0.45	1.41	0.46	(0.04, 0.02)
ING2	−1.16	0.32	1.43	0.47	(0.05, 0.01)
ING3	−1.38	1.18	1.56	0.33	(0.04, 0.02)
LIPS1	−2.34	−4.58	1.35	0.79	(0.01, 0.01, 0.01, 0.01, 0.01, 0.01)
LIPS2	−0.65	0.42	1.13	−	0.58
MAC	−0.2	−0.48	1.22	−	2.18
MIUR	−1.27	−2.53	1.21	3.81	(0.25, 0.01, 0.03, 0.06)
NGAL	−0.8	0.87	1.3	−	0.5
PELE	−1.61	−2.23	0.9	−	0.76
ROTH	−3.46	−8.11	1.56	1.06	(0.22, 0.03)
VELC	−20.04	−2.43	0.94	−	1.16
YASS	−1.24	1.69	1.36	0.37	0.06
FUTR	−2.43	7.75	4.62	−	6.8
GHAM	−1.02	6.06	1.68	−	1.41
GODO	−0.74	11.25	3.52	−	1.86
GYGI	−2.33	4.68	3.53	−	5.49
LEE	−1.23	8.72	4.1	1.68	(0.81, 0.79, 0.94)
LU	−0.59	5.82	1.35	−	3.01
NGAR	−2.04	21	3.22	3.53	(0.16, 0.26, 0.13, 0.21, 0.17, 0.21)
NEWM	−5.25	21.12	1.93	−	2.03
PENG	−2.26	−13.8	2.1	−	1.3
THAK	−1.44	7.51	5.72	4.99	(0.6, 0.3, 0.33)
WASH	−3.44	−23.24	2.82	−	6.57

3.2 Attenuation due to noise

In this Section, we state how the correlation between any two measured responses is smaller in magnitude than the true correlation between the responses, as long as the measurement noise is non-negligible. While this general result has long been established (Spearman 1904), we identify the specific parameters in the proposed model which govern the degree of attenuation. Specifically, the amount of attenuation depends on the scaling factors, G_k, as well as the replicate and experiment noise, θ_k and ξ_k.

Theorem 1

Consider two observed replicates, X₁, X₂, from two different experiments, measuring different response variables. For simplicity, let l[j] = j and k[j] = j, so that for instance, X_i,1 = L_i,1G₁ + E_i,1 + R_i,1 + ν₁. As specified in section 2.1, we assume without loss of generality that Var(L_i) = ψ_i,i = 1. Given ξ_k > 0 and θ_k > 0, for k = 1, 2;

$$\text{Cor}(X_1,X_2)=\frac{{\psi }_{1,2}}{\sqrt{1+({\xi }_1+{\theta }_1)/G_1^2}\sqrt{1+({\xi }_2+{\theta }_2)/G_2^2}}<{\psi }_{1,2}$$

holds for ψ_1,2 > 0.

3.3 Attenuation due to model mis-specification

In this Section we show that even if we account for noise by incorporating data from multiple experiments, if we do not account for the presence of structured noise within experiments, we still underestimate correlation. We prove this for a simplified case, where our model parameters are assumed to be homogeneous across responses, experiments and replicates.

We consider a model, ℳ, of the form as in Equations 1–4, with two response variables (N_L = 2), two experiments in each response (N_E = 4), and n/2 replicates for each experiment, (N_R = 2n replicates in total):

$$ℳ=(\mathbf{\Psi },[G_k],[{\xi }_k],[{\theta }_j]),k=1,\dots ,4\text{and}j=1,\dots ,2n$$ (11)

We assume that the parameters are homogeneous across response variables, experiments and replicates: ξ = ξ_k ≥ 0 and θ = θ_j > 0 for all k and j, and also assume G = G_k for all k.

Let ℳ̃ be another model, again, of the form of equations 1–4, but without an experiment specific random effect:

$$\mathrm{ℳ̃}=(\mathbf{\Psi ̃},[{\mathrm{G̃}}_k],[{\mathrm{\xi ̃}}_k=0],[{\mathrm{\theta ̃}}_j])$$ (12)

As above, we assume that θ̃ = θ̃_j > 0 and G̃ = G̃_k = 1 for all j and k. Aside from having no experiment specific random effect, the model two models are identical. That is, ℳ̃ has the same structure, Ñ_L = N_L = 2, Ñ_R = N_R = 2n.

Theorem 2

Consider data generated by model ℳ. Let ${\mathrm{\psi ̃}}_{1,2}^{\mathrm{P}\mathrm{M}}$ denote the posterior mean estimator of ψ_1,2 under the misspecified model, ℳ̃. The posterior mean asymptotically underestimates the true correlation as N, the number of mRNAs and proteins goes to infinity. That is,

$$\underset{N\to \infty }{\text{lim}}{\mathrm{\psi ̃}}_{1,2}^{\mathrm{P}\mathrm{M}}\le {\psi }_{1,2},$$ (13)

with equality only if ξ = 0.

3.4 Attenuation due to missing data

In this Section we explore the implications of neglecting to model a non-ignorable missing data mechanism. Since correlation cannot be computed with incomplete pairs of observations, a complete case analysis by definition ignores all mRNAs and proteins for which either value in the pair is missing. We consider a simplified complete case analysis, with a missingness mechanism on only one of the random variables, which induces missingness in the other. The result below states that when the the missingness mechanism generates an observed data distribution which has smaller variance than the complete data distribution, the complete case analysis (on observed pairs) leads to an underestimate of the true correlation.

This condition is generally consistent with the missing data mechanism we posit in Eq 5. That is, with a logistic missingness mechanism, the variance of the observed data is smaller than that of the complete data. As such, this result suggests that previous approaches that ignore the missing values for mRNA expression or protein abundance (complete case analyses) generally underestimate the correlation.

Theorem 3

Let (X, Y) be a bivariate normal random variable. Consider a missingness mechanism on X and denote the observed data, ignoring all censored observations, X^obs. Further, assume the missingness mechanism is such that Var(X^obs) < Var(X). In a complete-case analysis, the missingness mechanism on X also induces a stochastic censoring on Y, and only Y^obs is observed. If Cor(X, Y) > 0, then

$$\text{Cor}(X^{\text{obs}},Y^{\text{obs}})<\text{Cor}(X,Y).$$ (14)

4 Results

We evaluate our methodology on synthetic and real data. In Section 4.1, we show that the Bayesian confidence intervals have good frequentist coverage, especially for the parameters of interest. In Section 4.2, we show that the proposed model is fairly robust to departures from normality of the log-mRNA or log protein abundance levels. We also empirically show that the basic structure of the model is necessary, consistent with theoretical results in Section 3. In Section 4.3, we present the results of the meta-analysis analysis on the data sets listed in Table 1 and compare our results to previous estimates of the correlation between mRNA expression and protein correlation in yeast. In Section 4.4, we incorporate technology information into the model, and check the sensitivity of the estimated correlation to different assumptions about the magnitude of technology bias.

4.1 Frequentist coverage

We set out to evaluate frequentist coverage of the Bayesian intervals under realistic simulated data sets. We considered three scenarios for the true correlation, ψ_1,2 = 0.5, 0.8, and 0.9. Each scenario consists of 27 simulated experiments, 11 measuring gene expression and 16 measuring protein abundance, each with a number of replicated measurement matching a real data set in Table 1, and each measurement with 5,300 dimensions—corresponding to distinct genes and proteins. The remaining parameters (η_k, G_k, ξ_k, θ_j, for all j, k) were set to the posterior means reported in Table 6, which were obtained when fitting the model to the real data, to generate realistic data. Using these parameter values, we then simulated 100 replicated data collections for each correlation scenario.

Table 2 reports the frequentist coverage of the 50% and 95% Bayesian posterior intervals for the correlation ψ_1,2 and the other model parameters. For each of the three correlation scenarios (ψ_1,2 = 0.5, 0.8, and 0.9), we report the fraction of times the posterior interval covers the true correlation. For ξ_k, ${\eta }_k^0,{\eta }_k^1$ and G_k we report the average coverage, over the N_E experiment specific parameters. For ν_j and θ_j we report the coverage averaged over all N_R replicates in the data set. The coverage is excellent for most parameters, especially the main parameter of interest, ψ_1,2, and the experiment effect variances ξ_k.

Table 2.

Frequentist coverage of 50% (top row) and 95% (bottom row) Bayesian credible intervals, for various parameters. Data sets were generated with three true correlation levels: 0.5, 0.8, 0.9.

		Coverage for parameters
True φ1,2	Confidence	φ1,2	ξk	θj	Gk	νj	${\eta }_k^1$	${\eta }_k^0$
φ1,2 = 0.5	50%	43%	51%	39%	49%	40%	56%	54%
	95%	92%	95%	82%	94%	86%	96%	96%
φ1,2 = 0.8	50%	43%	50%	39%	45%	41%	55%	54%
	95%	94%	95%	82%	92%	83%	96%	96%
φ1,2 = 0.9	50%	49%	50%	40%	46%	39%	54%	54%
	95%	98%	95%	82%	93%	84%	96%	97%

4.2 Robustness to mis-specification

In this Section, we test the robustness of our model to departures from normality. Since it is not possible to observe the complete data, it is difficult to assess the left tail behavior of the complete data distribution for some data sets. To test how well our model performs for non-normal distributions with skew and heavier tails, we generate the mRNA expression and protein levels, L_i,l, using the asymmetric Laplace distribution. A standard multivariate asymmetric Laplace has the representation

$$\mathbf{Y}=\mathbf{m}X+X^{1/2}\mathbf{Z},$$ (15)

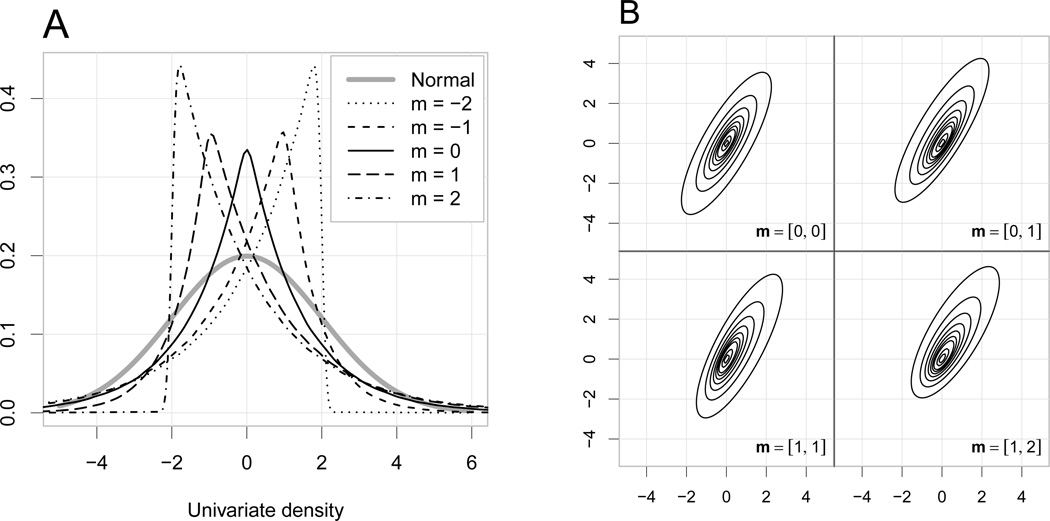
where Z ~ 𝒩_NL (0, Σ) and X is exponentially distributed with mean one (Kozubowski and Podgorski 2000). The asymmetric Laplace distribution is a continuous mixture of normals with exponentially distributed variance. The parameter m induces skewness. Figure 4 illustrates the univariate and bivariate asymmetric Laplace distributions for various values of the m skewness parameter.

Figure 4.

A) examples for asymmetric Laplace distributions for various shape parameters, the means of the distribution are matched to zero. B) examples for bivariate asymmetric Laplace distributions with ψ_1,2 = 0.8 and various m = [m₁, m₂] shape parameters.

We ran our algorithm on simulated data at three levels of correlation (0.5, 0.8 and 0.9) and varying skewness in the mRNA expression and protein levels. We again fixed the parameters to match those inferred from the true data (in Table 6) but this time generating L_i from an asymmetric Laplace (Equation 15) instead of the bivariate normal (Equation 2). Table 3 shows the inferred correlation for data generated using the multivariate asymmetric Laplace. While the model, as expected, gives biased correlation estimates for non-normal data, the bias is very small, even for very skewed and/or peaked data distributions.

Table 3.

Robustness of the model to departures from normality. The table shows inferred posterior mean correlations for data sets with multivariate asymmetric Laplace distributions, with varying correlation and skewness, fit using the normal model, Equation 1. Standard deviations are 0.01 or less for all values.

True Correlation	Asymmetric Laplace data, with skewness parameters m = [m1;m2]
	[0, 0]	[0, −1]	[0, 1]	[1, −1]	[1, 1]	[−1, −2]	[1, 2]
ψ1,2 = 0.5	0.49	0.45	0.55	0.48	0.47	0.46	0.50
ψ1,2 = 0.8	0.79	0.79	0.81	0.80	0.78	0.78	0.80
ψ1,2 = 0.9	0.90	0.90	0.91	0.90	0.89	0.90	0.89

Not only is the model robust to misspecification, but also, simpler models fail to give good estimates for at least some of the parameters. We conducted four kinds of experiments on synthetic data, the results of which are summarized in Table 4. All all four experiments we tested three different true ψ_1,2 values: 0.5, 0.8 and 0.9, with 10 runs for each of these values. All experiments used 5000 mRNAs and proteins.

• 1.First we show that modeling noise is important because noise attenuates correlation. Ignoring noise results in a downward bias in the inferred correlation. See Theorem 1. We generated noisy bivariate normal data with unit variance, one replicate for mRNA and one for protein levels, for 5000 mRNAs/proteins, with true correlations 0.5, 0.8 and 0.9. The noise level was ξ + θ = 0.8. Then we ignored the noise in our naive inference, i.e. we calculated the observed correlation of the noisy bivariate normal data.
• 2.Second, we show that ignoring the structure of the noise leads to attenuated correlation estimates. We use 16 mRNA expression and 16 protein replicates equally divided in 4 experiments for both. We generate noisy multivariate Normal data with this structure, with constant noise levels ξ_k[j] = 0.6 (experiment effects) and θ_j = 0.2 (replicate effects). The G_l[j] scaling parameter was one. Then we run the inference procedure by ignoring the experiment random effects, i.e. setting ξ_k = 0. See Theorem 2.
• 3a.Third, if part of the data is non-ignorably missing, then the correlation estimates are attenuated. We use 16 mRNA expression and 16 protein replicates equally divided in 4 experiments for both. We generate noisy multivariate Normal data with this structure, with constant noise levels ξ_k[j] = 0.6 (experiment effects) and θ_j = 0.2 (replicate effects). The G_l[j] scaling parameter was one. The parameters of the observation model were set arbitrarily in a way to get about 1000 completely observed mRNAs and proteins. In the inference we ignore the non-complete cases, and only use the (about 1000) completely observed mRNAs and proteins. See Theorem 3.
• 3b.Lastly, we show that imputing the missing data, but using a simpler, “missing at random” observation model fails to estimate correlation correctly. The synthetic data contained two experiments for both mRNA expression and protein levels, and two replicates for each experiments. The noise levels were set to ξ_k[j] = 0.6 and θ_j = 0.2, the parameters of the observation model were tuned to obtain about 1000 completely observed mRNAs and proteins. The missing data was then imputed by fitting the model using a MAR assumption instead of Equation 5. We find that using more experiments and/or more replicates tends to correct the bias in the inferred correlation. When the correlation is high, the conditional variance of a missing value, given all other observed values for the same mRNA or protein, will be small. With many good observed “surrogate measurements”, the results are somewhat robust to MAR assumptions.

Table 4.

Features of the data that attenuate correlation: noise, noise structure, missing data and non-randomly missing data. See text for the complete description. Standard deviations are 0.01 or less, unless shown otherwise.

	1. Noise	2. Structure	3a. Missing data	3b. Non-randomly missing data
ψ1,2	ψ̂1,2	ψ̂1,2	ψ̂1,2	ψ̂1,2
0.5	0.32	0.45	0.32 (± 0.07)	0.45 (± 0.02)
0.8	0.50	0.71	0.65 (± 0.02)	0.77 (± 0.03)
0.9	0.56	0.80	0.81 (± 0.03)	0.88 (± 0.02)

What about correlation between observations? In this research we assume that the measurements on each gene are independent observations with between replicate covariance, Σ. We consider correlation between genes in the experiment effects. Certain functionally related genes may in fact vary together across experiments in which the data are actually obtained in some condition which is close to, but not exactly, the one defined. Let E be the N × N_E random matrix of experiment specific random effects. We can augment the model to incorporate “between gene” row correlation, Δ, across the experiments:

$$\mathbf{E}~𝒩(\mathbf{0},\mathbf{\Delta }\otimes \mathit{\xi }),$$ (16)

where ξ is the diagonal matrix of experiment specific variances. We evaluate the effect of non-identity row correlation, Δ, in simulation. We consider simulations involving three different correlation structures between genes to evaluate how this influences the inference of latent mRNA-protein correlation at three different ψ_1,2 levels: 0.5, 0.8, and 0.9. In the first two cases we assume that the genes have a block correlation structure and that within blocks the genes are correlated at level 0.9. In two different simulations, we block the genes into 10 groups and 100 blocks of roughly equal size. In the third simulation we generate data with the gene correlation structure estimated from an independent Yeast data set under multiple conditions (Brem and Kruglyak 2005).

Row-wise correlation essentially decreases the effective sample size, leading to overconfidence in the inference (Efron 2009). Table 4.2 shows the 95% interval of the sampling distribution as well as the coverage of the 95% credible interval. As expected, there is significant loss of coverage, but the model estimates are essentially unbiased and the error is small. Thus the substantive conclusions on the data in Table 1 are not expected to change much in the presence of row-wise correlation in the noise.

Finally, we test how robust our model is to misspecification of the missingness mechanism. In particular, we assume a rather simple logistic form for the missingness of both mRNA and protein levels. There is evidence of more complicated missingness mechanisms, especially in studies using LC MS/MS to measure protein abundance. Here, a two-stage missingness mechanism, capturing both informative and non-informative censoring may be more appropriate Karpievitch et al. (2009). To account for a possible misspecification of this type, we generate data assuming that every protein is missing with a 20% probability, independent of its abundance in addition to the logistic censoring specified in Equation 5. The data was generated in a way such that the total fraction of missingess matched the true data. We generate data at three levels of true correlation (0.5, 0.8 and 0.9) and estimate this correlation using the one-level informative missingness model. There is no bias in the estimates, even though the missing data mechanism is slightly misspecified (0.50 ± .02, 0.80 ± .01, 0.9 ± .006). Since the marginal probability of missingness can be well approximated by our two-parameter observation model, the procedure is robust to more complex mechanisms.

4.3 Quantifying the transcriptional control of protein production

The main focus of this research is to identify the underlying true correlation between mRNA expression and protein abundance in exponentially growing yeast at steady state. Thus, we fit our model on the data listed in Table 1. When fitting the model on this data, we initialize our chains using standard software (Rosseel 2012) to find the EM solution, assuming data missing at random (Honaker et al. 2011), and use this as a starting point for our Gibbs sampler. To save disk space we save every 50th sample, and use over 5000 samples to generate posterior estimates. We checked the convergence of the MCMC simutaion for the ψ_1,2 samples, using two MCMC chains and the R̂ statistics of Gelman and Rubin (1992). In our real data fits, R̂ was close to 1 (less than 1.01), indicating very good convergence. The effective sample size for the inferred correlation, ψ_1,2, is 1427. The average effective sample size for the experiment noise within mRNA expression experiments is 3368 and for protein expression experiments is 1609.

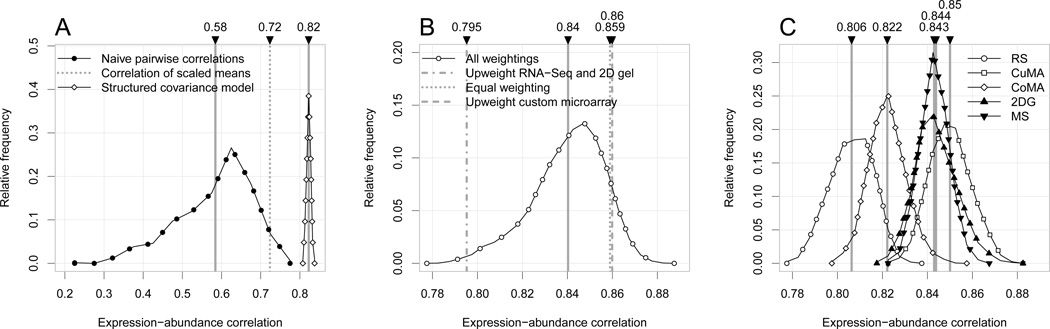
After accounting for the measurement structure, biological and technical noise, and missing data, we estimate the true posterior mean correlation to be 0.82 (± 0.01). This estimate is significantly larger than almost all previous estimates (Gygi et al. 1999; Ingolia et al. 2009) or estimates derived from naive complete-case analyses between single measurements (Figure 5A).

Figure 5.

A) mRNA expression–protein correlation estimates. The lines with filled and empty circles show all naive pairwise correlation estimates, using mRNAs measured in both data sets only, and the posterior distribution for the correlation, inferred via our structured covariance model, respectively. Dashed vertical lines correspond to mean values. The correlation of the (naive) average protein and mRNA expression levels over measurements is also shown. B) Posterior distribution of the correlation using the technology extension to our model, and discrete technology variance priors on all combinations over the weights 1, 2 and 5. The vertical lines show three weight configurations: the ones with the smallest and largest mean inferred correlation and the equal weighting (all weights equal to 1). C) Posterior distributions of mRNA expression–protein correlations, conditional on exactly one up weighted technology (W = [1, 1, 1, 1, 5]).

Some of our data sets have a very large number of measurements missing. To check that including them does not bias our results, we also fitted the model with exluding experiments with (1) more than 80% and (2) more than 60% of missingness. In both cases the inferred ψ_1,2 value was 0.83±0.01, comparable to the result obtained on the full data set, 0.82±0.01, in fact slightly higher.

These results have implications for our understanding of the role of post-transcriptional regulation in yeast at steady-state. In particular, they suggest that this type of regulation is not as pervasive as previously thought. Additionally, the data and our results suggest that, using the current technologies, yeast mRNA expression levels are not much worse for predicting protein abundance values in a given experiment than another protein abundance measurement from another lab. This is important because measuring mRNA expression levels is simpler and cheaper than measuring protein abundances. Thus, mRNA levels may in fact be a reasonable proxy for protein abundance, at least in steady state. A list of all experiment specific parameters are given in Table 6. The parameters, η, reflect the inferred missingness pattern by experiment, and the noise parameters ξ and θ reflect how much each experiment and replicate deviate from the inferred true gene expression or protein levels.

4.4 Assessing the impact of different measurement technologies

In our initial analysis, we assumed that for both mRNA expression and protein levels, all of the experiment level variables, E_i,k, are exchangeable. However, in reality there is further distinguishing information, namely, the technology that is used by each lab. In the literature, in addition to lab level effects, there is evidence of different systematic biases in the technologies (Wang et al. 2009; Roberts et al. 2011; Yuen et al. 2002). Incorporating these effects implies that experiments are only exchangeable if they are conducted using the same technology.

By introducing technology specific variables into the model, we can assess how sensitive the estimate of Ψ is to a model incorporating technology. For this analysis, we assume that each technology, t, has some bias, T_t, which is normally distributed with a technology specific variance. However, as noted by Larsson et al. (2013), the extent of technology specific bias and variation is not completely understood. As such, in our model, the technology specific biases have unknown variance terms that are impossible to infer without external data or prior knowledge. Thus, we perform a sensitivity analysis to check how our inferred correlation changes with different assumptions about this bias. We amend our model to incorporate technology information as follows:

$$X_{i,j}=T_{i,t[j]}{G}_{k[j]}+E_{i,k[j]}+R_{i,j}+{\nu }_{j,l[j]}$$ (17)

$$T_{i,t[j]}~𝒩(L_{i,l[j]},{\tau }_{l[j]}/W_{t[j]}),$$ (18)

with the rest of the model as defined in equations 2–5. Here, t[j] indexes a particular technology used for measuring replicate j. Technologies and experiments form nested groups. All replicates in a given experiment were performed using the same technology. Each technology is only used to measure either mRNA or protein levels. As before, E_i,k and R_i,j represent experiment and replicate specific effects.

W_t is a technology specific weight which can be fixed a priori or drawn from a distribution. The measured data alone cannot inform us about which technologies give more biased estimates. Accordingly, we fit our model, in separate runs, using different pre-chosen sets of weights, W, to explore the sensitivity of our results to possible biases in technology.

We consider three technologies for measuring mRNA expression (custom microarray, commercial microarray and RNA-Seq) and two technologies for measuring protein abundance (two-dimensional gel electrophoresis and mass spectrometry). For each technology, we assume W_t[j] is iid uniform over the set {1, 2, 5}. The values 1, 2, and 5 are arbitrary but representative of possible moderate and large technology specific biases. Under this assumption, the heavily weighted technology (W_t = 5) has bias with average magnitude that are $\sqrt{5}$ times smaller than the technologies assigned weight 1. Figure 5B shows the posterior mean correlation mixed over all combinations of weights. The mean correlation is slightly larger and more variable, but the qualitative results are qualitatively similar to those presented in Section 4.3. Figure 5C shows five conditional posteriors each with exactly one technology assigned weight 5 and the rest assigned weight 1.

Interestingly, the results in Figure 5C are nearly identical between protein abundance technologies, suggesting that mass spectrometry and the 2D gel technique imply biases of similar magnitude on Ψ̂. The results are more variable for the mRNA expression technologies. Weighting our estimate toward RNA-Seq yields the lowest correlation estimate (0.80) while weighting the estimate toward custom microarray yields a higher estimate (0.85). Crucially, when all technologies are given equal weight, the posterior mean correlation is close to the highest, at 0.86. Consistent with previous studies (Lu et al. 2007), this suggests that by combining data from experiments involving diverse technologies, we may in fact get better estimates than any one technology could give us on its own.

5 Discussion

We have presented an original meta-analysis of high-throughput biological data sets to quantify the coordination between transcription and translation, in yeast growin exponentially at steady state. Operationally, we have developed a hierarchical random effects model for log-transformed mRNA expression levels and protein concentrations, which includes a non-ignorable missing data mechanism. The correlation between latent representations of these two high-dimensional responses is the estimand of interest in our meta-analysis. This estimand is traditionally regarded as a nuisance parameter (e.g., Wang et al. 1996), thus we develop theory to assess the effects of noise, structured measurements, and non-ignorable missing data on the estimates, in Section 3.

We defined the correlation between latent mRNA and protein levels as the estimand of interest, to quantify the notion of coordination between transcription and translation. Our study is necessarily restricted to a single state of a simple organism, and has no direct implications for post-translational regulation in other settings, dynamically changing environments, other organisms, or regulation that cannot be measured by correlation (e.g. amplification of effects). Alternative notions of coordination are possible, however, some more justifiable than others. The correlation between observable measurements is a poor choice, for instance. More sophisticated approaches could consider a notion of an underlying biologic signal, quantified by means of categorial, or even simply binary, signal (Parmigiani et al. 2002). In the context of such approaches, it would then be natural define the correlation of these categorical, or binary, random variables as the estimand of interest.

Further evidence that illustrates the relevance and timeliness of estimates about the scalar estimand of interest here is given by a recent paper that targets the same estimand, in human (Li et al. 2014). In this paper, the authors report an estimate for the correlation between mRNA and protein levels of about 0.8, which is close to the estimate we report, but slightly lower, as can be expected given the complexity of a study in human.

Identifiability of random effects models is an outstanding issue and needs to be evaluated on a case-by-case basis. As detailed in Section 3.1, our model meets sufficient conditions for identifiability for the parameters L_i,l[j] and G_k[j] for all combinations of the indices i, j, k, l (e.g., Lee 2007, Sec. 2.2.2), but the non-ignorable missing data mechanism complicates the situation beyond the reach of available theory. However, the frequentist coverage results in Section 4.1 suggest that all the key parameters are identifiable. While these results were obtained on simulated data sets, the design of experiments matched closely the properties of the data collected for the meta-analysis, and parameter values were set to the estimated values obtained on the real data, thus adding confidence to the empirical identification.

We choose not to include information on estimates of the correlation between mRNA and protein levels reported in previous studies, including those whose data we included in the meta-analysis presented in Sections 4.3 and 4.4. This choice is motivated by the questionable statistical choices previous results depend on, including the use of complete cases only in the presence of non-ignorable missing data (caused by the measurement protocols implemented in the various technologies), the lack of modeling assumptions about important sources of variation in the data, or the lack of a model altogether. By not including previously reported correlations, we aimed at producing an independent analysis, based on a simple model that can be expected to produce robust estimates.

The exploratory data analysis summarized in Figure 2 suggests that the amount of missing data is inversely proportional to mRNA expression and protein concentration. This is expected, since even modern high-throughput technology find it difficult to complete the measurement protocols successfully for rare transcripts and proteins (Walther and Mann 2010; Soon et al. 2013). For convenience, we fully specified the non-ignorable missing data mechanism by means of a logistic regression, a well established approach (e.g., see Rubin and Little 2002; Ibrahim et al. 2005). Inference results were not sensitive to two alternative specifications of the (MNAR) missing data mechanism we considered; probit and log-log.

The assumption of normality of the log-transformed measurements of mRNA expression and protein concentration is another choice of convenience. We intended to carry out the meta-analysis with a model that included all the important sources of variation in the data, while simple enough to allow for some theoretical results on the correlation estimates. The multivariate normal distribution was an obvious choice. Exploratory data analysis suggested that log-transformed data are approximately normal. Goodness-of-fit evaluation by means of posterior predictive checks confirmed that the models in Sections 4.3 and 4.4 fit the data well. The simulation studies based on the multivariate asymmetric Laplace distribution for log-transformed data presented in Section 4.2, add further confidence that estimates of the correlation between mRNA and protein levels are robust to model mis-specifications.

5.1 Substantive conclusions

The main result of our meta-analysis is that the correlation between mRNA and protein levels, when estimated with a reasonable model, is much higher than previously reported. Our analyses indicate that a more accurate estimate of such correlation is between 0.82 and 0.86, depending on which model variant is used, the most conservative estimate being 0.82±0.01. The proportion of variance explained is expected to increase if one were to remove some of the within experiment variation by design. This could be accomplished, for instance, by using the same sample for both mRNA and protein quantification, by preparing the sample under conditions that are demonstrably steady-state and not altered by a transient stress response, or by using measurement technology with improved precision and accuracy. While our study is restricted to a simple organism and a well-defined condition, the analysis indicates that there has been widespread overestimation of the role of post-transcriptional regulation in these conditions (Gygi et al. 1999; Ingolia et al. 2009), and that suggests that other dominant modes of regulation are not waiting to be discovered.

Interestingly, the sensitivity analysis that incorporates technology information into the model suggests that the highest estimated correlation is obtained when we assume a bias of equal magnitude across technologies. This result is consistent with previous work that suggest improved estimates can be achieved by averaging across technologies (Lu et al. 2007). While there is debate about the best high-throughput technology, this result suggests that consolidating data from different sources, under the assumption that all technologies are equally good, balances out the biases from any individual approach. In other words, new technology is not necessarily better, than older but more mature technology.

Technology alone, however, does not explain all of the variability between different experiments. We hypothesize that much of the between experiment variability is due to disparity in growth rates at time of harvest. Even though the studies in our data collection claim to analyze samples from exponentially growing yeast, it is plausible that the growth rates differ due to experimental protocols. As evidence of this, preliminary results suggest that the scaling factors, G_k[j], are highly correlated with independent estimates of growth rate (Airoldi et al. 2009). We further explore this hypothesis elsewhere (Csárdi et al. 2013).

Ultimately, our meta-analysis analysis highlights the dangers of casually using correlations between observables to estimate the strength of the coordination between processes in the cell. We have shown that noise, missing data and model mis-specification can lead to spurious conclusions, in theory, and they actually do in practice.

Table 5.

The 95% interval of the sampling distribution of the posterior mean when experiment noise is correlated between genes. The results show that the estimate of ψ_1,2 is essentially unbiased but the variation increases as the degree of between gene correlation increases. The fourth column shows the coverage of the 95% credible interval. While there is significant undercoverage, the error is small.

	2.5%	Mean	97.5%	Coverage
ψ = 0.5, 10 blocks	0.46	0.50	0.52	0.81
ψ = 0.5, 100 blocks	0.47	0.50	0.52	0.91
ψ = 0.5, Brem et al	0.48	0.50	0.52	0.90
ψ = 0.8, 10 blocks	0.77	0.79	0.81	0.59
ψ = 0.8, 100 blocks	0.79	0.80	0.81	0.89
ψ = 0.8, Brem et al	0.78	0.80	0.82	0.74
ψ = 0.9, 10 blocks	0.86	0.89	0.91	0.28
ψ = 0.9, 100 blocks	0.89	0.90	0.91	0.76
ψ = 0.9, Brem et al	0.88	0.90	0.91	0.60

A Proofs

A.1 Theorem 1

Proof

Let ψ_1,2 = Cor(L₁, L₂). Then the covariance between the observed measurements X₁ and X₂ is Cov(X₁,X₂) = G₁G₂ψ_1,2 by equations 1–4. Finally, using equation 8 for the observed data variance, we have

$$\text{Cor}(X_1,X_2)=\frac{G_1{G}_2{\psi }_{1,2}}{\sqrt{G_1^2+{\xi }_1+{\theta }_1}\sqrt{G_2^2+{\xi }_2+{\theta }_2}}$$ (19)

$$=\frac{{\psi }_{1,2}}{\sqrt{1+({\xi }_1+{\theta }_1)/G_1^2}\sqrt{1+({\xi }_2+{\theta }_2)/G_2^2}}$$ (20)

$$<{\psi }_{1,2}.$$ (21)

A.2 Theorem 2

Proof

In the proof, we don’t need to assume that the latent response variances are fixed, they can vary freely. This is because the G_k = G̃_k = 1 restriction already ensures identifiability. We denote this new model, without unit variances, by ℳ^p. Similarly, our new misspecified model without unit variances is denoted by ℳ̃^p. Models ℳ and ℳ̃ will be a special case of the proof.

Bunke and Milhaud (1998) show, under mild conditions satisfied here, that when the MLE converges to a unique value, the posterior mean converges almost surely to that same value. Thus, instead of working with the posterior mean ${\mathrm{\psi ̃}}_{1,2}^{\mathrm{P}\mathrm{M}}$, it suffices to prove that the inequality holds for the MLE: ${\mathrm{\psi ̃}}_{1,2}^{\mathrm{M}\mathrm{L}\mathrm{E}}\le {\psi }_{1,2}$, with equality only if ξ = 0.

Figure 6: The structure of the covariance matrix Σ of the true model ℳ^p (left) and the covariance matrix Σ̃ of the misspecified model ℳ̃^p (right), from Theorem 2. The marginal variances of the replicates are σ² = θ + ξ + ϕ + γ and σ̃² = θ̃ + ϕ̃ + γ̃ and the experiment covariances are ε = ξ + ϕ + γ.

Consider multivariate normal data X = [X₁, …,X_2n] generated from the true model ℳ^p. Under ℳ^p, Cov(X) = Σ can be written as

$$\mathbf{\Sigma }={\mathbf{\Sigma }}_1\oplus {\mathbf{\Sigma }}_1+\gamma {\mathbf{1}}_{2n}{\mathbf{1}}_{2n}^{\prime },{\mathbf{\Sigma }}_1=(\theta {\mathbf{I}}_{n/2}+\xi {\mathbf{1}}_{n/2}{\mathbf{1}}_{n/2}^{\prime })\oplus (\theta {\mathbf{I}}_{n/2}+\xi {\mathbf{1}}_{n/2}{\mathbf{1}}_{n/2}^{\prime })+\varphi {\mathbf{1}}_n{\mathbf{1}}_n^{\prime },$$ (22)

where ⊕ is the direct sum operator, and 1_n is the constant one column vector with n rows. In (22) we define ψ₁ = ψ₂ = γ + ϕ. As noted at the beginning of the proof, we do not assume that ψ₁ = ψ₂ = 1, since fixing G_k = G̃_k = 1 ensures identifiability for both models. We also assume γ ≥ 0, θ > 0, ξ ≥ 0, ϕ ≥ 0. The correlation between the responses can be written as ψ_1,2 = γ/(ϕ+γ) now.

The misspecified model ℳ̃^p has covariance matrix Σ̃, with the following structure:

$$\mathbf{\Sigma ̃}=(\mathrm{\theta ̃}{\mathbf{I}}_n+\mathrm{\varphi ̃}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime })\oplus (\mathrm{\theta ̃}{\mathbf{I}}_n+\mathrm{\varphi ̃}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime })+\mathrm{\gamma ̃}{\mathbf{1}}_{2n}{\mathbf{1}}_{2n}^{\prime },$$ (23)

where γ̃ ≥ 0, θ̃ > 0, ϕ̃ ≥ 0. Again, we do not assume ψ̃₁ = ψ̃₂ = 1 here, and ψ̃₁ = ψ̃₂ = ϕ̃+γ̃, and the correlation between the responses is ψ̃_1,2 = γ̃/(ϕ̃ + γ̃).

Figure 6 shows the strucure of both the true Σ and the misspecified Σ̃.

First, we reparameterize Σ̃ in terms of its eigenvalues. We present three properties about the eigenstructure of Σ̃:

1. Σ̃1_2n = (θ̃+nϕ̃+2nγ̃)1_2n, so $1/\sqrt{2n}{\mathbf{1}}_{2n}$ is a normalized eigenvector of Σ̃ with eigenvalue θ̃ + nϕ̃ + 2nγ̃. This can be seen easily by performing the matrix-vector product:

   $$\mathbf{\Sigma ̃}{\mathbf{1}}_{2n}=\left[\begin{array}{c}\hfill (\mathrm{\theta ̃}{\mathbf{I}}_n+\mathrm{\varphi ̃}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }){\mathbf{1}}_n\hfill \\ \hfill (\mathrm{\theta ̃}{\mathbf{I}}_n+\mathrm{\varphi ̃}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }){\mathbf{1}}_n\hfill \end{array}\right]+2n\mathrm{\gamma ̃}{\mathbf{1}}_{2n}=\left[\begin{array}{c}\hfill (\mathrm{\theta ̃}+n\mathrm{\varphi ̃}){\mathbf{1}}_n\hfill \\ \hfill (\mathrm{\theta ̃}+n\mathrm{\varphi ̃}){\mathbf{1}}_n\hfill \end{array}\right]+2n\mathrm{\gamma ̃}{\mathbf{1}}_{2n}=$$ (24)

   $$=(\mathrm{\theta ̃}+n\mathrm{\varphi ̃}){\mathbf{1}}_{2n}+2n\mathrm{\gamma ̃}{\mathbf{1}}_{2n}=(\mathrm{\theta ̃}+n\mathrm{\varphi ̃}+2n\mathrm{\gamma ̃}){\mathbf{1}}_{2n}.$$ (25)
2. Let ${\mathbf{1}}_{2n}^{\pm }$ be a column vector with n ones on the top and n minus ones on the bottom: ${\mathbf{1}}_{2n}^{\pm }=[{\mathbf{1}}_n|-{\mathbf{1}}_n]\prime$. Then $\mathbf{\Sigma ̃}{\mathbf{1}}_{2n}^{\pm }=(\mathrm{\theta ̃}+n\mathrm{\varphi ̃}){\mathbf{1}}_{2n}^{\pm }$ so $1/\sqrt{2n}{\mathbf{1}}_{2n}^{\pm }$ is a normalized eigenvector of Σ̃ with eigenvalue θ̃ + nϕ̃

   $$\mathbf{\Sigma ̃}{\mathbf{1}}_{2n}^{\pm }=\left[\begin{array}{c}\hfill (\mathrm{\theta ̃}{\mathbf{I}}_n+\mathrm{\varphi ̃}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }){\mathbf{1}}_n\hfill \\ \hfill -(\mathrm{\theta ̃}{\mathbf{I}}_n+\mathrm{\varphi ̃}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }){\mathbf{1}}_n\hfill \end{array}\right]+{\mathbf{0}}_{2n}=\left[\begin{array}{c}\hfill (\mathrm{\theta ̃}+n\mathrm{\varphi ̃}){\mathbf{1}}_n\hfill \\ \hfill -(\mathrm{\theta ̃}+n\mathrm{\varphi ̃}){\mathbf{1}}_n\hfill \end{array}\right]=(\mathrm{\theta ̃}+n\mathrm{\varphi ̃}){\mathbf{1}}_{2n}^{\pm }.$$ (26)
3. The remaining 2n−2 eigenvalues are all equal to θ̃. To see this, we show that if a vector v is orthogonal to both 1_2n and ${\mathbf{1}}_{2n}^{\pm }$, then it is an eigenvector of Σ̃ with eigenvalue θ̃. We partition v into two blocks of equal size: v = [v^⊤|v^⊥]′. If v is orthogonal to 1_2n, then its elements sum up to zero. If it is orthogonal to ${\mathbf{1}}_{2n}^{\pm }$, then the elements of both v^⊤ and v^⊥ sum up to zero as well. So we have

   $$\mathbf{\Sigma ̃}\mathbf{v}=\left[\begin{array}{c}\hfill (\mathrm{\theta ̃}{\mathbf{I}}_n+\mathrm{\varphi ̃}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }){\mathbf{v}}^{\top }\hfill \\ \hfill (\mathrm{\theta ̃}{\mathbf{I}}_n+\mathrm{\varphi ̃}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }){\mathbf{v}}^{\perp }\hfill \end{array}\right]+{\mathbf{0}}_{2n}=\left[\begin{array}{c}\hfill (\mathrm{\theta ̃}{\mathbf{v}}^{\top })\hfill \\ \hfill (\mathrm{\theta ̃}{\mathbf{v}}^{\perp })\hfill \end{array}\right]=\mathrm{\theta ̃}\mathbf{v}.$$ (27)

Thus, our eigendecomposition is $\mathbf{\Sigma ̃}={\lambda }_1{\mathbf{v}}_1{\mathbf{v}}_1^{\prime }+{\lambda }_2{\mathbf{v}}_2{\mathbf{v}}_2^{\prime }+{\lambda }_3{\mathbf{V}}_3$, where

$${\lambda }_1=\mathrm{\theta ̃}+n\mathrm{\varphi ̃}+2n\mathrm{\gamma ̃},{\mathbf{v}}_1{\mathbf{v}}_1^{\prime }=\frac{1}{2n}{\mathbf{1}}_{2n}{\mathbf{1}}_{2n}^{\prime },$$ (28)

$${\lambda }_2=\mathrm{\theta ̃}+n\mathrm{\varphi ̃},{\mathbf{v}}_2{\mathbf{v}}_2^{\prime }=\frac{1}{2n}{\mathbf{1}}_{2n}^{\pm }({\mathbf{1}}_{2n}^{\pm })\prime ,$$ (29)

$${\lambda }_3=\mathrm{\theta ̃},{\mathbf{V}}_3=(\mathbf{I}-\frac{1}{n}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime })\oplus (\mathbf{I}-\frac{1}{n}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }),$$ (30)

and we will parameterize Σ̃ with λ₁, λ₂, λ₃ instead of θ̃, ϕ̃ and γ̃.

The likelihood of a covariance matrix Φ, for X is given by

$$\mathbf{ℒ}(\mathbf{\Phi }|\mathbf{X})={(2\pi )}^{-N(n_1+n_2)/2}\prod _{i=1}^N[\text{det}{(\mathbf{\Phi })}^{-1/2}\text{exp}(-\frac{1}{2}{\mathbf{X}}_i^{\prime }{\mathbf{\Phi }}^{-1}{\mathbf{X}}_i)],$$ (31)

and the log-likelihood is

$$\text{log}\mathbf{ℒ}(\mathbf{\Phi }|\mathbf{X})=-\frac{N(n_1+n_2)}{2}\text{log}(2\pi )-\frac{1}{2}\sum _{i=1}^N\text{log det}(\mathbf{\Phi })-\frac{1}{2}\sum _{i=1}^N({\mathbf{X}}_i^{\prime }{\mathbf{\Phi }}^{-1}{\mathbf{X}}_i),=-\frac{N(n_1+n_2)}{2}\text{log}(2\pi )-\frac{N}{2}\text{log det}(\mathbf{\Phi })-\frac{1}{2}\text{tr}((N-1)\mathbf{S}{\mathbf{\Phi }}^{-1}),$$ (32)

where S is the sample covariance matrix of X.

For a given data set, N is constant, so we can divide (32) by N/2 and omit the constant terms to get

$$\text{log}\mathbf{ℒ}(\mathbf{\Phi }|\mathbf{X})\propto -\text{log det}(\mathbf{\Phi })-\text{tr}(\frac{N-1}{N}\mathbf{S}{\mathbf{\Phi }}^{-1}).$$ (33)

In the limit as N → ∞, (N − 1)/N → 1 and S → Σ elementwise with probability 1. Since the likelihood function is continuous, the log-likelihood is simply

$$\underset{N\to \infty }{\text{lim}}\text{log}ℒ(\mathbf{\Phi }|\mathbf{X})\propto \text{log}\mathrm{ℒ̃}(\mathbf{\Phi }|\mathbf{\Sigma })=-\text{log det}(\mathbf{\Phi })-\text{tr}(\mathbf{\Sigma }{\mathbf{\Phi }}^{-1}),$$ (34)

by the continuous mapping theorem. We maximize log ℒ̃ over Φ, where Φ is of the same form as Σ̃ (Eq 23). For simplicity we use Σ̃ instead of Φ in the following.

We find the maximum of log ℒ̃ as a function of λ₁, λ₂ and λ₃. Since the parameter space is not compact we first evaluate the log likelihood at the boundaries. It is easy to see that at each boundary, the log likelihood diverges to negative infinity:

$$\underset{\mathrm{\theta ̃}\to \infty }{\text{lim}}\text{log}\mathrm{ℒ̃}=\underset{\mathrm{\theta ̃}\to 0}{\text{lim}}\text{log}\mathrm{ℒ̃}=\underset{\mathrm{\varphi ̃}\to \infty }{\text{lim}}\text{log}\mathrm{ℒ̃}=\underset{\mathrm{\gamma ̃}\to \infty }{\text{lim}}\text{log}\mathrm{ℒ̃}=-\infty .$$ (35)

If at least one of θ̃, ϕ̃ or γ̃ goes to infinity, then at least one eigenvalue of Σ̃ goes to infinity (see equations 28–30), so −log det(Φ) goes to negative infinity and the second term of the log likelihood is a finite constant. If θ̃ → 0, then the first term goes to positive infinity, the second to negative infinity, but because of the logarithm, the second term dominates and the likelihood goes to negative infinity. This means that the likelihood has a global maximum in the interior of the parameter space.

At the MLE, the derivative of the log-likelihood must vanish. Differentiating the log-likelihood in terms of an arbitrary parameter p gives

$$\frac{\mathrm{d}\text{log}\mathrm{ℒ̃}}{\mathrm{d}p}=-\text{tr}\left({\mathbf{\Sigma ̃}}^{-1}\frac{\mathrm{d}\mathbf{\Sigma ̃}}{\mathrm{d}p}\right)+\text{tr}\left({\mathbf{\Sigma ̃}}^{-1}\frac{\mathrm{d}\mathbf{\Sigma ̃}}{\mathrm{d}p}{\mathbf{\Sigma ̃}}^{-1}\mathbf{\Sigma }\right),$$ (36)

where we use the fact that

$$\frac{\mathrm{d}\text{det}(\mathbf{\Sigma ̃})}{\mathrm{d}p}=\text{tr}\left({\mathbf{\Sigma ̃}}^{-1}\frac{\mathrm{d}\mathbf{\Sigma ̃}}{\mathrm{d}p}\right),\frac{\mathrm{d}{\mathbf{\Sigma ̃}}^{-1}}{\mathrm{d}p}=-{\mathbf{\Sigma ̃}}^{-1}\frac{\mathrm{d}\mathbf{\Sigma ̃}}{\mathrm{d}p}{\mathbf{\Sigma ̃}}^{-1}.$$ (37)

The derivatives in terms of the three parameters are

$$\frac{\mathrm{d}\mathbf{\Sigma ̃}}{\mathrm{d}{\mathrm{\lambda }}_1}={\mathbf{v}}_1{\mathbf{v}}_1^{\prime },\frac{\mathrm{d}\mathbf{\Sigma ̃}}{\mathrm{d}{\mathrm{\lambda }}_2}={\mathbf{v}}_2{\mathbf{v}}_2^{\prime },\frac{\mathrm{d}\mathbf{\Sigma ̃}}{\mathrm{d}{\mathrm{\lambda }}_3}={\mathbf{V}}_3.$$ (38)

In the following, we use the fact that Σ̃v₁ = λ₁v₁ and Σ̃⁻¹ v₁ = 1/λ₁v₁ and set the first partial derivative to zero.

$$\frac{\mathrm{d}\text{log}\mathbf{ℒ̃}}{\mathrm{d}{\mathrm{\lambda }}_1}=-\text{tr}\left(\frac{1}{{\mathrm{\lambda }}_1}{\mathbf{v}}_1{\mathbf{v}}_1^{\prime }\right)+\text{tr}\left(\frac{1}{{\mathrm{\lambda }}_1^2}{\mathbf{v}}_1{\mathbf{v}}_1^{\prime }\mathbf{\Sigma }\right)=0,$$ (39)

which, using ${\mathbf{v}}_1{\mathbf{v}}_1^{\prime }=1/(2n){\mathbf{1}}_{2n}{\mathbf{1}}_{2n}^{\prime }$, simplifies to

$$-\frac{1}{{\mathrm{\lambda }}_1}+\frac{1}{2n{\mathrm{\lambda }}_1^2}(4n^2\gamma +2n^2\varphi +n^2\xi +2n\theta ).$$ (40)

From here we can easily see that the MLE of λ₁ is

$${\mathrm{\lambda }}_1^{\mathrm{M}\mathrm{L}\mathrm{E}}=2n\gamma +n\varphi +\frac{1}{2}n\xi +\theta .$$ (41)

A similar argument leads to the MLE for λ₂:

$${\mathrm{\lambda }}_2^{\mathrm{M}\mathrm{L}\mathrm{E}}=n\varphi +\frac{1}{2}n\xi +\theta .$$ (42)

For the third parameter we have

$$\frac{\mathrm{d}\text{log}\mathbf{ℒ̃}}{\mathrm{d}{\mathrm{\lambda }}_3}=-\text{tr}\left(\frac{1}{{\mathrm{\lambda }}_3}{\mathbf{V}}_3\right)+\text{tr}(\frac{1}{{\mathrm{\lambda }}_3^2}{\mathbf{V}}_3\mathbf{\Sigma })=0.$$ (43)

The second term is the trace of

$$\frac{1}{{\lambda }_3^2}{\mathbf{V}}_3\mathbf{\Sigma }=\frac{1}{{\lambda }_3^2}[({\mathbf{I}}_n-\frac{1}{n}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime })\oplus ({\mathbf{I}}_n-\frac{1}{n}{\mathbf{1}}_n{\mathbf{1}}_n^{\prime })]\mathbf{\Sigma }=\frac{1}{{\lambda }_3^2}[\mathbf{\Sigma }-\frac{1}{n}({\mathbf{1}}_n{\mathbf{1}}_n^{\prime }\oplus {\mathbf{1}}_n{\mathbf{1}}_n^{\prime })\mathbf{\Sigma }]=$$ (44)

$$=\frac{1}{{\lambda }_3^2}[\mathbf{\Sigma }-\frac{1}{n}(\frac{{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }\mathbf{\Sigma }}{n^2\gamma {\mathbf{1}}_n{\mathbf{1}}_n^{\prime }}|\frac{n^2\gamma {\mathbf{1}}_n{\mathbf{1}}_n^{\prime }}{{\mathbf{1}}_n{\mathbf{1}}_n^{\prime }\mathbf{\Sigma }}\left)\right],$$ (45)

and the trace itself is

$$\text{tr}(\frac{1}{{\lambda }_3^2}{\mathbf{V}}_3\mathbf{\Sigma })=\frac{1}{{\lambda }_3^2}(2n\theta +2n\varphi +2n\xi +2n\gamma -\frac{2}{n}(n^2\varphi +n^2\gamma +\frac{n^2}{2}\xi +n\theta ))=$$ (46)

$$=\frac{1}{{\mathrm{\lambda }}_3^2}((2n-2)\theta +n\xi ).$$ (47)

Using this with equation 43, we get

$$2(n-1)\frac{1}{{\mathrm{\lambda }}_3}=\frac{1}{{\mathrm{\lambda }}_3^2}((2n-2)\theta +n\xi ),{\mathrm{\lambda }}_3^{\mathrm{M}\mathrm{L}\mathrm{E}}=\theta +\frac{n}{2n-2}\xi .$$ (48)

Going back to the original parameterization is easy:

$$\mathrm{\theta ̃}={\mathrm{\lambda }}_3,\mathrm{\varphi ̃}=\frac{{\mathrm{\lambda }}_2-{\mathrm{\lambda }}_3}{n},\mathrm{\gamma ̃}=\frac{{\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2}{2n},$$ (49)

and yields

$${\mathrm{\theta ̃}}^{\mathrm{M}\mathrm{L}\mathrm{E}}=\theta +\frac{n}{2n-2}\xi ,{\mathrm{\varphi ̃}}^{\mathrm{M}\mathrm{L}\mathrm{E}}=\varphi +\frac{n-2}{2n-2}\xi ,{\mathrm{\gamma ̃}}^{\mathrm{M}\mathrm{L}\mathrm{E}}=\gamma .$$ (50)

To show that the posterior mean of the misspecified model underestimates the true correlation, we need to show that

$$({\mathrm{\psi ̃}}_{1,2}^{\mathrm{P}\mathrm{M}}={\mathrm{\psi ̃}}_{1,2}^{\mathrm{M}\mathrm{L}\mathrm{E}}=)\frac{{\mathrm{\gamma ̃}}^{\mathrm{M}\mathrm{L}\mathrm{E}}}{{\mathrm{\varphi ̃}}^{\mathrm{M}\mathrm{L}\mathrm{E}}+{\mathrm{\gamma ̃}}^{\mathrm{M}\mathrm{L}\mathrm{E}}}=\frac{\gamma }{{\mathrm{\varphi ̃}}^{\mathrm{M}\mathrm{L}\mathrm{E}}+\gamma }\le \frac{\gamma }{\varphi +\gamma }(={\psi }_{1,2}).$$ (51)

This is equivalent to ϕ̃^MLE ≥ ϕ, which holds, with equality only if ξ = 0. This completes the proof.

A.3 Theorem 3

Proof

Denote ρ = Cor(X, Y) > 0 and ρ^obs = Cor(X^obs, Y^obs). Assume, without loss of generality, that X and Y have mean zero and unit variance. We can write Y as

$$Y=\rho X+\sqrt{1-{\rho }^2}Z,$$ (52)

where Z is a standard normal, independent of X. By assumption, we only observe X^obs, with Var(X^obs) = c, with 0 < c < 1. By equation 52, we then have

$$Y^{\text{obs}}=\rho X^{\text{obs}}+\sqrt{1-{\rho }^2}Z$$ (53)

$$\text{Var}(Y^{\text{obs}})={\rho }^2\text{Var}(X^{\text{obs}})+(1-{\rho }^2)\text{Var}(Z)$$ (54)

$$={\rho }^{2}c+1-{\rho }^2=(1-{\rho }^2)(1-c)+c>c.$$ (55)

Similarly, Cov(X^obs, Y^obs) = ρc. Assuming ρ > 0, it is true that

$${\rho }^{\text{obs}}=\frac{\text{Cov}(X^{\text{obs}},Y^{\text{obs}})}{\sqrt{\text{Var}(X^{\text{obs}})}\sqrt{\text{Var}(Y^{\text{obs}})}}=\frac{c\rho }{\sqrt{c}\sqrt{\text{Var}(Y^{\text{obs}})}}<\frac{c\rho }{\sqrt{c}\sqrt{c}}=\rho .$$ (56)

B Additional figures and tables

Figure 7: Distribution of observed and imputed mRNA and protein levels, in different experiment, together with the logistic censoring probability. A: LEE protein abundance data, B: LU protein abundance data, C: CAUS mRNA expression data set.

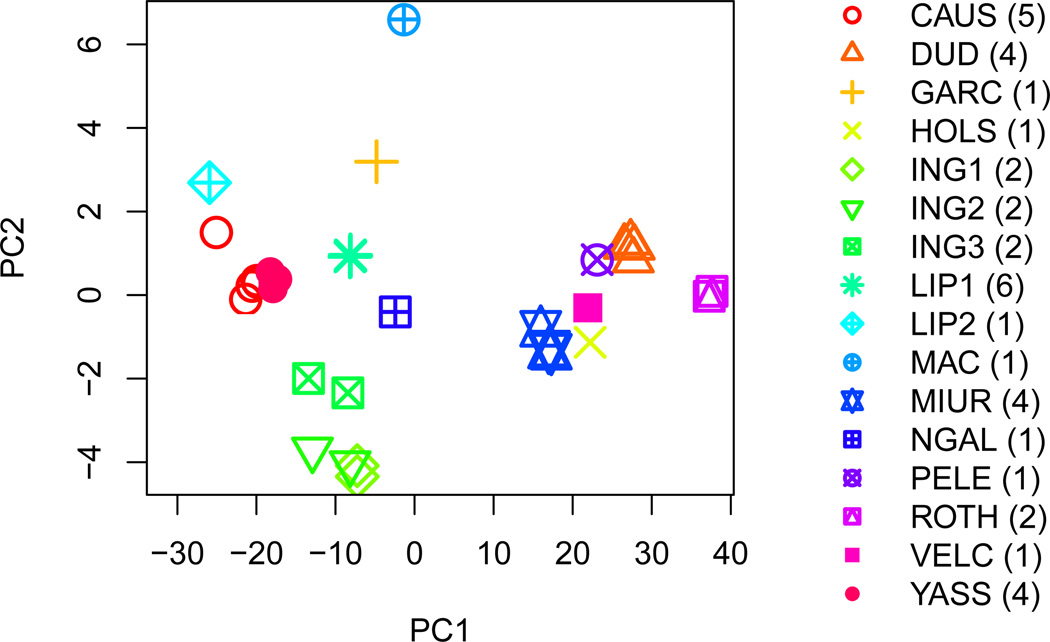
Figure 8: Principal component analysis of the mRNA replicates. Only mRNAs that were measured in all replicates, are included here, 390 genes in total. It is clear that most of the variation is according to the lab, where the experiment was performed. In the case of the Lipson and Ingolia labs, the two and three batches are also apparent and motivate our choice to treat these as separate experiments.

Table 7.

Details about missing data. The tables show the number of proteins (left) and mRNAs (right) with a given number of observations. The number of observations is in the first columns, the number of proteins/mRNAs with that many observation in the second columns, and the number of proteins/mRNAs with at most that many observations in the third columns.

Proteins
# obs.	# prot.	cumul. # prot.
0	813	813
1	445	1258
2	249	1507
3	131	1638
4	79	1717
5	72	1789
6	129	1918
7	334	2252
8	689	2941
9	624	3565
10	453	4018
11	342	4360
12	290	4650
13	235	4885
14	180	5065
15	191	5256
16	194	5450
17	204	5654
18	135	5789
19	49	5838
20	16	5854

mRNAs
# obs.	# mRNAs	cumul. # mRNAs
0	2	2
1	1	3
2	2	5
3	1	6
4	2	8
5	2	10
6	37	47
7	21	68
8	13	81
9	12	93
10	21	114
11	12	126
12	18	144
13	24	168
14	22	190
15	28	218
16	36	254
17	41	295
18	56	351
19	33	384
20	30	414
21	21	435
22	30	465
23	23	488
24	40	528
25	49	577
26	76	653
27	90	743
28	107	850
29	160	1010
30	210	1220
31	342	1562
32	370	1932
33	497	2429
34	685	3114
35	924	4038
36	809	4847
37	617	5464
38	390	5854