Understanding scaling through history-dependent processes with collapsing sample space

Significance

Many complex systems reduce their flexibility over time in the sense that the number of options (possible states) diminishes over time. We show that rank distributions of the visits to these states that emerge from such processes are exact power laws with an exponent −1 (Zipf’s law). When noise is added to such processes, meaning that from time to time they can also increase the number of their options, the rank distribution remains a power law, with an exponent that is related to the noise level in a remarkably simple way. Sample-space-reducing processes provide a new route to understand the phenomenon of scaling and provide an alternative to the known mechanisms of self-organized criticality, multiplicative processes, or preferential attachment.

Abstract

History-dependent processes are ubiquitous in natural and social systems. Many such stochastic processes, especially those that are associated with complex systems, become more constrained as they unfold, meaning that their sample space, or their set of possible outcomes, reduces as they age. We demonstrate that these sample-space-reducing (SSR) processes necessarily lead to Zipf’s law in the rank distributions of their outcomes. We show that by adding noise to SSR processes the corresponding rank distributions remain exact power laws, $p\left(x\right)\sim x^{-\lambda }$, where the exponent directly corresponds to the mixing ratio of the SSR process and noise. This allows us to give a precise meaning to the scaling exponent in terms of the degree to which a given process reduces its sample space as it unfolds. Noisy SSR processes further allow us to explain a wide range of scaling exponents in frequency distributions ranging from $\alpha =2$ to $\infty$. We discuss several applications showing how SSR processes can be used to understand Zipf’s law in word frequencies, and how they are related to diffusion processes in directed networks, or aging processes such as in fragmentation processes. SSR processes provide a new alternative to understand the origin of scaling in complex systems without the recourse to multiplicative, preferential, or self-organized critical processes.

A typical feature of aging is that the number of possible states in a system reduces as it ages. Whereas a newborn can become a composer, politician, physicist, actor, or anything else, the chances for a 65-y-old physics professor to become a concert pianist are practically zero. A characteristic feature of history-dependent systems is that their sample space, defined as the set of all possible outcomes, changes over time. Many aging stochastic systems (such as career paths) become more constrained in their dynamics as they unfold (i.e., their sample space becomes smaller over time). An example for a sample-space-reducing (SSR) process is the formation of sentences. The first word in a sentence can be sampled from the sample space of all existing words. The choice of subsequent words is constrained by grammar and context, so that the second word can only be sampled from a smaller sample space. As the length of a sentence increases, the size of the sample space of word use typically reduces.

Many history-dependent processes are characterized by power-law distribution functions in their frequency and rank distributions of their outcomes. The most famous example is the rank distribution of word frequencies in texts, which follows a power law with an approximate exponent of −1, the so-called Zipf’s law (1). Zipf’s law has been found in countless natural and social phenomena, including gene expression patterns (2), human behavioral sequences (3), fluctuations in financial markets (4), scientific citations (5, 6), distributions of city (7) and firm sizes (8, 9), and many more (see, e.g., ref. 10). (Some of these examples are, of course, not associated with SSR processes.) Over the past decades there has been a tremendous effort to understand the origin of power laws in distribution functions obtained from complex systems. Most of the existing explanations are based on multiplicative processes (11–14), preferential mechanisms (15–17), or self-organized criticality (18–20). Here we offer an alternative route to understand scaling based on processes that reduce their sample space over time. We show that the emergence of power laws in this way is related to the breaking of a symmetry in random sampling processes, a mechanism that was explored in ref. 21. History-dependent random processes have been studied generically (22, 23), however not with the rationale to understand the emergence of scaling in complex systems.

Results

The Pure SSR Process and Zipf's Law.

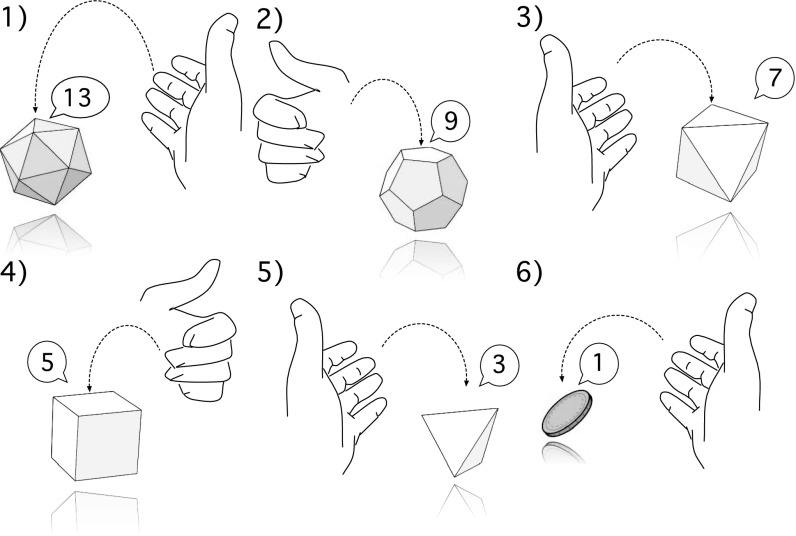
The essence of SSR processes can be illustrated by a set of N fair dice with different numbers of faces. The first dice has one face, the second has two faces (coin), the third one three, and so on, up to dice number N, which has N faces. The faces of a dice are numbered and have respective face values. To start the SSR process, take the dice with the largest number of faces (N) and throw it. The result is a face value between 1 and N; say it is K. We now take dice number $K-1$ (with $K-1$ faces) and throw it, to get a number i between 1 and $K-1$; say we throw L. We now take dice number $L-1$, throw it, and so forth. We repeat the process until we reach dice number 1, and the process stops. We denote this directed and acyclic process by ϕ. As the process unfolds, ϕ generates a single sequence of strictly decreasing numbers i. An intuitive realization of this process is depicted in Fig. 1. The probability that the process ϕ visits the particular site i in a sequence is the visiting probability $P_N\left(i\right)$, which can easily be shown to follow an exact Zipf’s law, $P_N\left(i\right)=1/i$. This is done, for example, with a proof by induction on N. Take the process ϕ and let $N=2$. There exist two possible sequences: Either ϕ directly generates a 1 with probability $1/2$, or ϕ first generates 2 with probability $1/2$, and then a 1 with certainty. Both sequences visit 1 but only one visits 2. As a consequence, $P_2\left(2\right)=1/2$ and $P_2\left(1\right)=1$. Let us now suppose that $P_{N\prime }\left(i\right)=1/i$ has been shown up to level $N^{\prime }=N-1$. Now, if the process starts with dice N, the probability to hit i in the first step is $1/N$. Also, any other j, $N\ge j>i$, is reached with probability $1/N$. If we get $j>i$, we will obtain i in the next step with probability $P_{j-1}\left(i\right)$, which leads us to the recursive scheme for all $i<N$, $P_N\left(i\right)=\frac{1}{N}\left(1+{\displaystyle {\sum }_{i<j\le N}{P}_{j-1}\left(i\right)}\right).$ Because by assumption $P_{j-1}\left(i\right)=1/i$, with $i<j\le N$ holds, simple algebra yields $P_N\left(i\right)=1/i$. Finally, as pointed out above, for $i=N$, we have $P_N\left(N\right)=1/N$, which completes the proof that indeed the visiting probability is

$$P_N\left(i\right)=\frac{1}{i}.$$ [1]

Fig. 1.

SSR process. Imagine a set of $N=20$ dice with different numbers of faces. We start by throwing the 20-faced dice (icosahedron). Suppose we get a face value of 13. We now have to take the 12-faced dice (dodecahedron), throw it, and get a face value of, say, 9, so that we must continue with the 8-faced dice. Say we throw a 7, forcing us to take the (ordinary) dice, with which we throw, say, a 5. With the 4-faced dice we get a 2, which forces us to take the 2-faced dice (coin). The process ends when we throw a 1 for the first time. The set of possible outcomes (sample space) reduces as the process unfolds. The sequence above was chosen to make use of the platonic dice for pictorial reasons only. If the process is repeated many times, the distribution of face values (rank-ordered) gives Zipf’s law.

If the process ϕ is repeated many times, meaning that once it reaches dice number 1 we start by throwing dice number N again, we are interested in how often a given site i is occupied on average. The occupation probability for site i, given that there are N possible sites, is denoted by $p_N\left(i\right)$. Note an important property of the process ϕ. Although in general the visiting probability $P_N$ and the occupation probability $p_N$ of a process quantify different aspects, for the particular process ϕ both probabilities only differ by a normalization factor. This is so because any sequence generated by ϕ is strictly decreasing and contains any particular site i at most once. Further, any sequence ends on site 1, meaning $P_N\left(1\right)=1$. Therefore, it is clear that $P_N\left(i\right)=p_N\left(i\right)/p_N\left(1\right)$, where $p_N\left(1\right)$ is a normalization factor. This shows that this prototype of an SSR processes exhibits an exact Zipf’s law in the (rank-ordered) occupation probabilities.

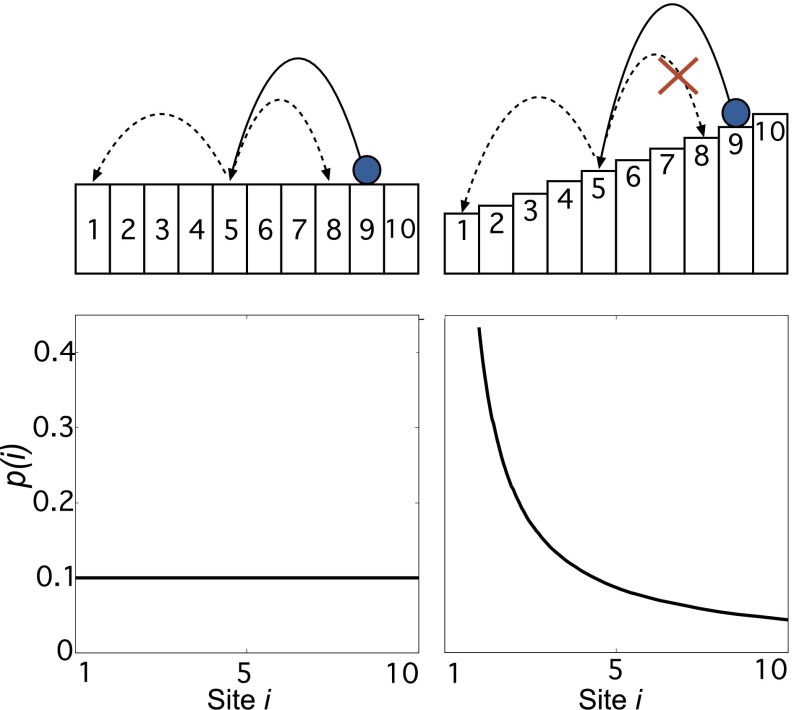
An alternative picture that illustrates the history-dependence aspect of the same SSR processes is shown in Fig. 2. In Fig. 2, Left we show an independent and identically distributed (iid) stochastic process, where the space of potential outcomes is $\mathrm{\Omega }=\left\{1,\dots ,N\right\}$. At each time step a ball can jump from one of N sites of $\mathrm{\Omega }$ to any other with equal probability. Because the process is independent, the conditional probability of jumping from site i to site j is $P\left(j|i\right)=1/N$. There is no path dependence. If we define ${\mathrm{\Omega }}_i$ as the subset of those sites that can be reached from site i, we obviously find that this is constant over time,

$${\mathrm{\Omega }}_1={\mathrm{\Omega }}_2=\dots ={\mathrm{\Omega }}_N=\mathrm{\Omega }.$$

We refer to this process as an unconstrained random walk and denote it by ${\varphi }_R$. The occupation distribution is $p\left(i\right)=1/N$ (Fig. 2). To introduce path or history dependence, assume that sites are arranged in levels like a staircase. Now imagine a ball that can bounce downstairs to lower levels randomly but never can climb to higher levels (Fig. 2, Right). If at time t the ball is at level (site) i, at $t+1$ all lower levels $j<i$ can be reached with the same probability, $P\left(j|i\right)=1/\left(i-1\right)$. Jumps to higher levels are forbidden, $P\left(j|i\right)=0$, for $j\ge i$. The process ends at the lowest stair level 1. In this process, sample space displays a nested structure,

$${\mathrm{\Omega }}_1\subset {\mathrm{\Omega }}_2\subset \dots \subset {\mathrm{\Omega }}_N\subset \mathrm{\Omega }.$$

In this case, ${\mathrm{\Omega }}_i=\left\{\mathrm{1,2},\cdots ,i-1\right\}$, for all values of $i\in \Omega$. ${\Omega }_1$ is the empty set. This nested structure of sample space is the defining property of SSR processes. This type of nesting breaks the left–right symmetry of the iid stochastic process. The visiting probability to sites (levels) i during a downward sequence is again $P_N\left(i\right)=1/i$. Because this process is equivalent to ϕ, the same proof applies.

Fig. 2.

Illustration of path dependence, SSR, and nestedness of sample space. (Left) Unconstrained (iid) random walk ${\varphi }_R$ realized by a ball randomly bouncing between all possible sites. The probability to observe the ball at a given site i is uniform, $p\left(i\right)=1/N$. (Right) The ball can only bounce downward; the left–right symmetry is broken. When level 1 is reached the process stops and is repeated. Sample space reduces from step to step in a nested way (main feature of SSR processes). After many iterations the occupation distribution (visits to level i) follows Zipf’s law, $p_{N=10}\left(i\right)\propto i^{-1}$. Symmetry breaking of the sampling changes the uniform probability distribution to a power law.

The Role of Noise in SSR Processes.

It is conceivable that in many real systems nestedness of SSR processes is not realized perfectly and that from time to time the sample space can also expand during a sequence. In the above example this would mean that from time to time random upward moves are allowed, or equivalently, that the nested process ϕ is perturbed by noise. In the context of the scenario depicted in Fig. 2 we look at a superposition of the SSR ϕ and the unconstrained random walk ${\varphi }_R$. Using λ to denote the mixing ratio, the nested SSR process ${\Phi }^{\left(\lambda \right)}$ with noise is written as

$${\Phi }^{\left(\lambda \right)}=\lambda \varphi +\left(1-\lambda \right){\varphi }_R,\lambda \in \left[\mathrm{0,1}\right].$$ [2]

More concretely, if the ball is at site i, with probability λ it jumps (downward) to any of site $k\in {\Omega }_i$ (with uniform probability), and with probability $1-\lambda$ it jumps to any of the N sites, $\left(j\in \Omega \right)$. In other words, each time before throwing the dice we decide with probability λ that the sample space for the next throw is ${\Omega }_i$ (SSR process), or with $\left(1-\lambda \right)$ it is $\Omega$ (iid noise ${\varphi }_R$). We repeat this process until the face value 1 is obtained. With probability λ the process is ϕ and stops, and with probability $\left(1-\lambda \right)$ the process is ${\varphi }_R$ and continues until 1 occurs again. Obviously, $\lambda =0$ corresponds to the unconstrained random walk, and $\lambda =1$ recovers the results for the strictly SSR processes without noise. Note that for $0\le \lambda <1$, ${\Phi }_{\lambda }$ may visit a given site i more than once. This implies in general that the visiting probability $P_N^{\left(\lambda \right)}\left(i\right)$ and the occupation probability $p_N^{\left(\lambda \right)}\left(i\right)$ no longer need to be proportional to each other. For that reason we now explicitly compute the occupation probability $p_N^{\left(\lambda \right)}\left(i\right)$ for SSR processes with a given noise level. For simplicity in notation we now suppress N and write $p^{\left(\lambda \right)}\left(i\right)$.

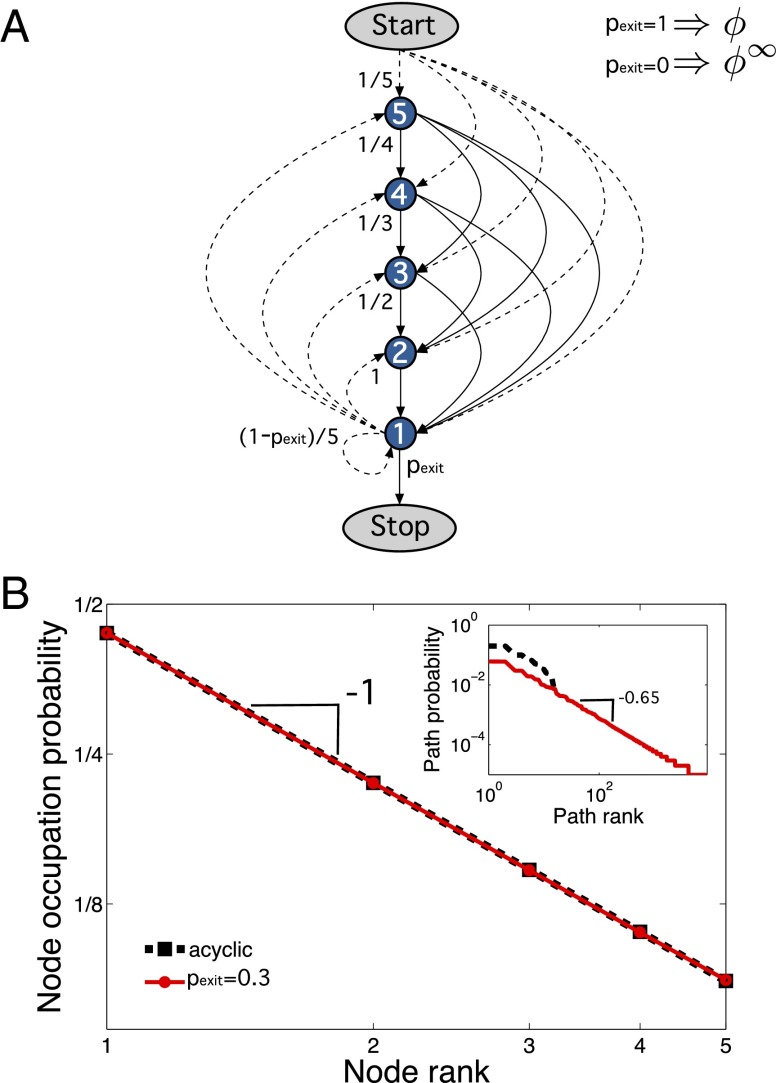
Note that ϕ produces one realization of $2^{N-1}$ possible sequences of sites $i=1,\cdots ,N$, and then stops. The maximum length of such a sequence is N, the average sequence length is $l\sim \log N$. In contrast, the unconstrained random walk ${\varphi }_R$ has no stopping criterion. To avoid problems with mixing processes with different lengths we replace ϕ with a process ${\varphi }^{\infty }$ that is identical to ϕ, except for the case when site $i=1$ is reached. In that case ${\varphi }^{\infty }$ does not stop but continues with tossing the N-faced dice and thus restarts the process ϕ (in the numerical simulations we stop the process after M restarts). For ${\varphi }^{\infty }$ site $i=1$ becomes both the starting point of a new single-sequence process ϕ, and the end point of the previous one (see also Fig. 5A). Replacing ϕ by ${\varphi }^{\infty }$ in Eq. 2 ensures that we have an infinitely long, noisy sequence, which is denoted by ${\Phi }_{\infty }^{\left(\lambda \right)}=\lambda {\varphi }^{\infty }+\left(1-\lambda \right){\varphi }_R$. Successive restarting gives us the possibility to treat SSR processes as stationary, for which the consistency equation

$$p^{\left(\lambda \right)}\left(i\right)={\displaystyle \sum _{j=1}^{N}P\left(i|j\right)\hspace{0.17em}{p}^{\left(\lambda \right)}\left(j\right)}$$ [3]

holds. Here $P\left(i|j\right)$ is the conditional probability that site i is reached from site j in the next time step in an infinite and noisy SSR process. It reads

$$P\left(i|j\right)=\{\begin{array}{ll}\frac{\lambda }{j-1}+\frac{1-\lambda }{N}\hfill & \text{for}i<j\hfill \\ \frac{1-\lambda }{N}\hfill & \text{for}i\ge j>1\hfill \\ \frac{1}{N}\hfill & \text{for}i\ge j=1.\hfill \end{array}$$ [4]

The first line in the above equation accounts for the strictly SSR process, the second line for the unconstrained random walk component, and the third line takes care of the restarting once site $i=1$ is reached. From Eqs. 3 and 4 we get

$$p^{\left(\lambda \right)}\left(i\right)=\frac{1-\lambda }{N}+\frac{1}{N}{p}^{\left(\lambda \right)}\left(1\right)+{\displaystyle \sum _{j=i+1}^N\frac{\lambda }{j-1}\hspace{0.17em}{p}^{\left(\lambda \right)}\left(j\right)}.$$ [5]

Clearly, the recursive relation $p^{\left(\lambda \right)}\left(i+1\right)-p^{\left(\lambda \right)}\left(i\right)=-\lambda \frac{1}{i}{p}^{\left(\lambda \right)}\left(i+1\right)$ holds, from which one obtains

$$\begin{array}{c}\frac{p^{\left(\lambda \right)}\left(i\right)}{p^{\left(\lambda \right)}\left(1\right)}={\displaystyle \prod _{j=1}^{i-1}{\left(1+\frac{\lambda }{j}\right)}^{-1}}=\exp \left[-{\displaystyle \sum _{j=1}^{i-1}\log \left(1+\frac{\lambda }{j}\right)}\right]\\ \sim \exp \left(-{\displaystyle \sum _{j=1}^{i-1}\frac{\lambda }{j}}\right)\sim \exp \left(-\lambda \log \left(i\right)\right)=i^{-\lambda }.\end{array}$$

$p^{\left(\lambda \right)}\left(1\right)$ is given by the normalization condition ${\displaystyle {\sum }_i{p}^{\left(\lambda \right)}\left(i\right)}=1$, and we arrive at the remarkable result

$$p^{\left(\lambda \right)}\left(i\right)\propto i^{-\lambda }.$$ [6]

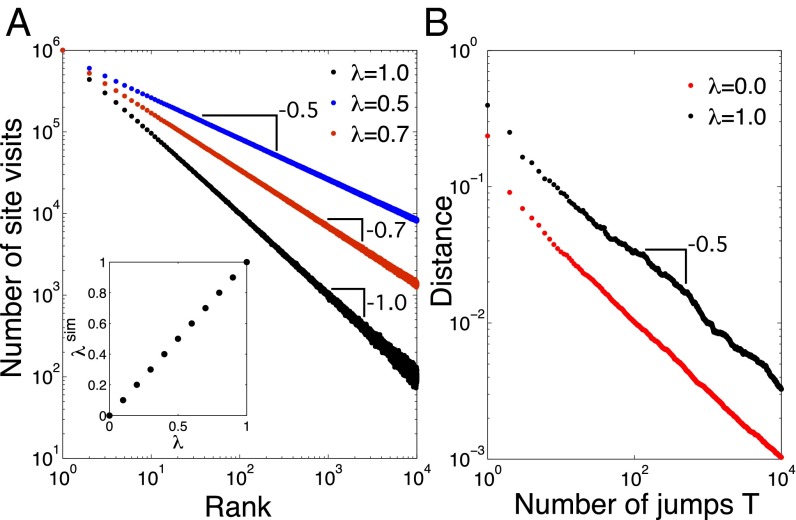
Note that λ is nothing but the mixing parameter for the noise component. For $\lambda =1$ one recovers Zipf’s law, $p^{\left(\lambda =1\right)}\left(i\right)\propto i^{-1}$; for $\lambda =0$, the uniform distribution $p^{\left(\lambda =0\right)}\left(i\right)=1/N$ is obtained. For intermediate $0<\lambda <1$ one observes an asymptotically exact power law with exponent λ. Note that Eq. 6 is a statement about the rank distribution of the system. Often statistical features of systems are presented as frequency distributions, that is, the probability that a given site (state) is visited k times, $\tilde{p}\left(k\right)$, and not as rank distributions. These are related, however. It is well known that if the rank distribution p is a power law with exponent λ, $\tilde{p}$ is also a power law with the exponent $\alpha =\frac{1+\lambda }{\lambda }$ (see, e.g., ref. 10). The result of Eq. 6 implies that we are able to understand a remarkable range of exponents in frequency distributions, $\alpha \in \left[2,\infty \right)$, by noisy SSR processes. Many observed systems in nature display frequency distributions with exponents between 2 and 3, which in our framework relates to a mixing ratio of $\lambda >0.5$. We find perfect agreement of the result of Eq. 6 and numerical simulations (Fig. 3A). The slope of the measured rank distributions in log scale, ${\lambda }^{\text{sim}}$, perfectly agree with the theoretical prediction λ. Fitting was carried out by using the method proposed in ref. 24.

Fig. 5.

(A) SSR processes seen as random walks on networks. A random walker starts at the start node and diffuses through the directed network. Depending on the value of $p_{\text{exit}}$, two possible types of walks are possible. For $p_{\text{exit}}=1$, the finite ($2^{N-1}=16$ possible paths) and acyclic process ϕ is recovered that stops after a single path; for $p_{\text{exit}}=0$, we have the infinite and cyclical process, ${\varphi }^{\infty }$. For $p_{\text{exit}}>0$ we have the mixed process, ${\Phi }^{\text{mix}}=p_{\text{exit}}\varphi +\left(1-p_{\text{exit}}\right){\varphi }^{\infty }$. (B) The occupation probability for ${\Phi }^{\text{mix}}$ is unaffected by the value of $p_{\text{exit}}$. The repeated ϕ (dashed black line) and the mixed process with $p_{\text{exit}}=0.3$ (solid red line) have exactly the same occupation probability $p_N\left(i\right)$, which corresponds to the stationary visiting distribution of nodes in the ${\varphi }^{\infty }$ network by random walkers. (Inset) Rank distribution of path-visit frequencies. Clearly they depend strongly on $p_{\text{exit}}$. Whereas the acyclic ϕ produces a finite distribution, the cyclic one produces a power law, matching the theoretical prediction of ref. 27. For the simulation we generated $5\cdot {10}^5$ sequence samples and found $\mathrm{32,523}$ distinct sequences for $p_{\text{exit}}=0.3$.

Fig. 3.

(A) Rank distributions of SSR processes with iid noise contributions from simulations of Φ^(λ)_∞, for three values of λ = 1, 0.7, and 0.5 (black, red, and blue, respectively). Fits to the distributions [obtained with a maximum-likelihood estimator (24)] yield λ^fit = 0.999, λ^fit = 0.699, and λ^fit = 0.499, respectively. Clearly, an almost exact match with the expected power-law exponents is realized. The inset shows the dependence of the measured exponent λ^sim from the simulations (slope), on various noise levels λ. The exponent λ^sim is practically identical to λ. N = 10,000, numerical simulations were stopped after M = 10⁶ restarts of the process. (B) Convergence rate. The distance (2-norm) between the simulated occupation probability (normalized histogram) after T jumps in the Φ^(λ)_∞ process, and the predicted power-law of Eq. 6, is shown for λ = 1 (black), and the pure random case, λ = 0 (red). Both distances show a power-law convergence ∼T^−β. MLE fits yield β = 0.512 and 0.463, for λ = 0 and 1, respectively. This means that both cases are compatible with β ∼ 1/2, and that SSR processes converge equally fast toward their limiting distributions as pure random walks do.

Convergence Speed of SSR Distributions.

From a practical side the question arises of how fast SSR processes converge to the limiting occupation distribution given by Eq. 6. In other words, what is the distance between the sample distribution p^(λ)_T of the process Φ^(λ)_∞ and p^(λ), after T individual jumps? In Fig. 3B we show the Euclidean distance of the distribution after T jumps $p_T^{\left(\lambda \right)}$, and $p^{\left(\lambda \right)}$, ${\Vert p_T^{\left(\lambda \right)}-p^{\left(\lambda \right)}\Vert }_2=\sqrt{{\displaystyle {\sum }_{i\in \mathrm{\Omega }}{\left[p_T^{\left(\lambda \right)}\left(i\right)-p^{\left(\lambda \right)}\left(i\right)\right]}^2}}$. We find that the distance decays as

$${\Vert p_T^{\left(\lambda \right)}-p^{\left(\lambda \right)}\Vert }_2\sim T^{-\frac{1}{2}}.$$ [7]

The result does not depend on the value of λ. For the pure random case $\lambda =0$, our result for the convergence rate is well known and is in full accordance with the Berry–Esseen theorem (25), which accounts for the rate of convergence of the central limit theorem for iid processes. The fact that for $\lambda =1$ we see the same convergence behavior means that SSR processes converge equally fast to their underlying limiting power-law distribution.

Examples

Sentence Formation and Zipf’s Law.

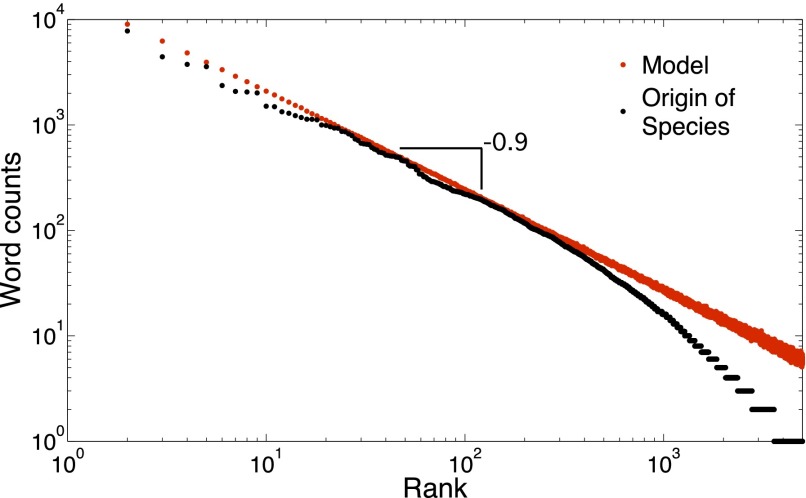
One example for a SSR process of the presented type is the process by which sentences are formed. During the creation of a sentence, grammatical and contextual constraints have the effect of a reducing sample space [i.e., the space (vocabulary) from which a successive word in a sentence can be sampled]. Clearly, the process of sentence formation is not expected to be strictly SSR, and we expect deviations from an exact Zipf’s law in the rank distribution of words in texts. In Fig. 4 we show the empirical distribution of word frequencies of Darwin’s The Origin of Species, which shows an approximate power law with a rank exponent of $\gamma \sim 0.9$. In our framework of the mixed process ${\Phi }_{\infty }^{\left(\lambda \right)}$ this corresponds to a mixing parameter $\lambda =0.9$, indicating that in the process of sentence formation nesting is not perfect, and many instances occur where sample space can expand from one word to another. Note that here M corresponds to the number of sentences in a text. In the simulation we use $N=\mathrm{5,000}$ words and $M=\mathrm{10,000}$ restarts. For a more detailed model of sentence formation and SSR processes, see ref. 26.

Fig. 4.

Empirical rank distribution of word frequencies in The Origin of Species (black), showing two power-law regimes. For the most frequent words, the distribution is approximately power-law with an exponent $\gamma \sim 0.9$. The corresponding distribution for the ${\Phi }^{\left(\lambda \right)}$ process with $\lambda =0.9$ (red), suggests a slight deviation from perfect nesting. This means that in sentence formation, about 90% of consecutive word pairs, sample space is strictly reducing. Simulation: $N=\mathrm{5,000}$ (words), and $M=\mathrm{10,000}$ restarts (sentences).

SSR Processes and Random Walks on Networks.

SSR processes can be related to random walks on directed networks, as depicted in Fig. 5A. There we start the process from a start node, from which we can reach any of the N nodes with probability $1/N$. At whatever node we end up, we can successively reach nodes with lower node numbers until we reach node number 1. There, with probability $p_{\text{exit}}$ we jump to a stop node that ends the process. Note that if $p_{\text{exit}}=1$, the process runs through one single path and then stops. The process is acyclic and finite; there are $2^{N-1}$ possible paths. This network diffusion process is equivalent to the process ϕ above. However, if $p_{\text{exit}}=0$, the process becomes cyclic and infinite and corresponds exactly to ${\varphi }^{\infty }$. For any $p_{\text{exit}}>0$ we have a mixing of the two processes, ${\Phi }^{\text{mix}}=p_{\text{exit}}\varphi +\left(1-p_{\text{exit}}\right){\varphi }^{\infty }$, which is again cyclic, and the number of possible paths is infinite. In Fig. 5B we show the result for the node occupation distribution for the process ${\Phi }^{\text{mix}}$ for $p_{\text{exit}}=1$ (dashed black line) and $p_{\text{end}}=0.3$ (solid red line). The figure is produced from $5\cdot {10}^5$ independently sampled sequences generated by ${\Phi }^{\text{mix}}$. As expected the distribution follows the exact Zipf law, irrespective of the value of $p_{\text{exit}}$. The process ${\Phi }^{\text{mix}}$ allows us to study also the rank distribution of paths through the network. The path that is most often taken through the network has rank 1, the second most popular path has rank 2, and so on. Recent theoretical work (27) predicts a difference in the corresponding distributions for different values of $p_{\text{exit}}$. According to ref. 27, acyclic processes are expected to show finite path rank distributions of no particular shape. This is seen in Fig. 5B, Inset (black dashed line), which shows the observed path rank distribution for the $2^{N-1}=16$ paths. For cyclic processes where at least one node participates in at least two distinct cycles ref. 27 predicts power laws, which we clearly confirm for the cyclic ${\Phi }^{\text{mix}}$ process with $p_{\text{exit}}=0.3$ (red line). Note that in our example node 1 alone is involved in five distinct cycles. The process ${\Phi }^{\text{mix}}$ demonstrates the mechanism that produces these power laws in its simplest form, where the probability of long sequences are products of the probability of the finite number of possible sequences that they concatenate.

SSR Processes and Fragmentation Processes.

One important class of aging systems are fragmentation processes, such as objects that repeatedly break at random sites into ever smaller pieces (see, e.g., refs. 28 and 29). A simple example demonstrates how fragmentation processes are related to SSR processes. Consider a stick of a certain initial length L, such as a spaghetto, and mark some point on the stick. Now take the stick and break it at a random position. Select the fragment that contains the mark and record its length. Then break this fragment again at a random position, take the fragment containing the mark, and again record its length. One repeats the process until the fragment holding the mark reaches a minimal length, say the diameter of an atom, and the fragmentation process stops. The process is clearly of the SSR type because fragments are always shorter than the fragment they come from. In particular, if the mark has been chosen on one of the endpoints of the initial strand of spaghetti, then the consecutive fragmentation of the marked fragment is obviously a continuous version of the SSR process ϕ discussed above. Note that even though the length sequence of a single marked fragment is an SSR process, the size evolution of all fragments is more complicated, because fragment lengths are not independent from each other: Every spaghetti fragment of length x splits into two fragments of respective lengths, $y<x$ and $x-y$. The evolution of the distribution of all fragment sizes was analyzed in ref. 29. Note that in the one-dimensional SSR processes introduced here we see no signs of multiscaling. However, this possibility might exist for continuous or higher-dimensional versions of SSR processes.

Discussion

The main result of Eq. 6 is remarkable insofar as it explains the emergence of scaling in an extremely simple and hitherto unnoticed way. In SSR processes, Zipf’s law emerges as a simple consequence of breaking a directional symmetry in stochastic processes, or, equivalently, by a nestedness property of the sample space. More general power exponents are simply obtained by the addition of iid random fluctuations to the process. The relation of exponents and the noise level is strikingly simple and gives the exponent a clear interpretation in terms of the extent of violation of the nestedness property in strictly SSR processes. We demonstrate that SSR processes converge equally fast toward their limiting distributions, as uncorrelated iid processes do.

We presented several examples for SSR processes. The emergence of scaling through SSR processes can be used straightforwardly to understand Zipf’s law in word frequencies. An empirical quantification of the degree of nestedness in sentence formation in a number of books allows us to understand the variations of the scaling exponents between the individual books (26). SSR processes can be related to diffusion processes on directed networks. For a specific example we demonstrated that the visiting times of nodes follow a Zipf’s law, and could further reproduce very general recent findings of path-visit distributions in random walks on networks (27). Here we presented results for a complete directed graph; however, we conjecture that SSR processes on networks and the associated Zipf’s law of node-visiting distributions are tightly related and are valid for much more general directed networks. We demonstrated how SSR processes can be related to fragmentation processes, which are examples of aging processes. We note that SSR processes and nesting are deeply connected to phase-space collapse in statistical physics (21, 30–32), where the number of configurations does not grow exponentially with system size (as in Markovian and ergodic systems), but grows subexponentially. Subexponential growth can be shown to hold for the phase-space growth of the SSR sequences introduced here. In conclusion, we believe that SSR processes provide a new alternative view on the emergence of scaling in many natural, social, and man-made systems. It is a self-contained, independent alternative to multiplicative, preferential, self-organized criticality and other mechanisms that have been proposed to understand the origin of power laws in nature (33).