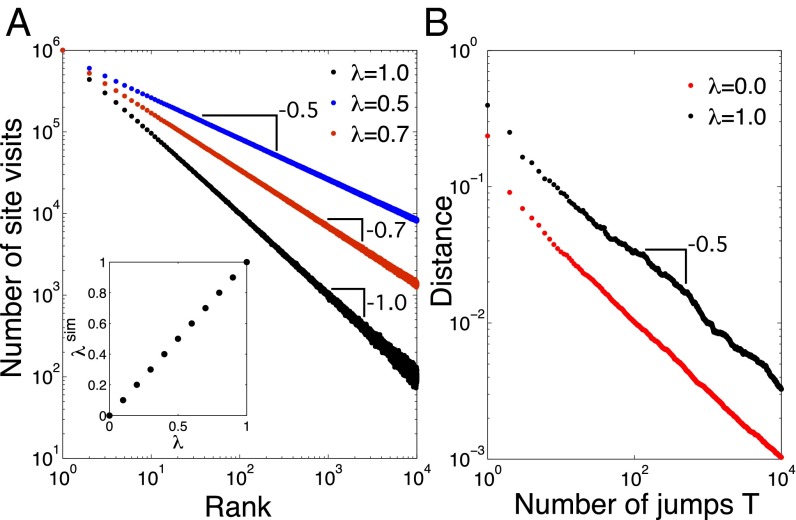
Fig. 3.

(A) Rank distributions of SSR processes with iid noise contributions from simulations of Φ^(λ)_∞, for three values of λ = 1, 0.7, and 0.5 (black, red, and blue, respectively). Fits to the distributions [obtained with a maximum-likelihood estimator (24)] yield λ^fit = 0.999, λ^fit = 0.699, and λ^fit = 0.499, respectively. Clearly, an almost exact match with the expected power-law exponents is realized. The inset shows the dependence of the measured exponent λ^sim from the simulations (slope), on various noise levels λ. The exponent λ^sim is practically identical to λ. N = 10,000, numerical simulations were stopped after M = 10⁶ restarts of the process. (B) Convergence rate. The distance (2-norm) between the simulated occupation probability (normalized histogram) after T jumps in the Φ^(λ)_∞ process, and the predicted power-law of Eq. 6, is shown for λ = 1 (black), and the pure random case, λ = 0 (red). Both distances show a power-law convergence ∼T^−β. MLE fits yield β = 0.512 and 0.463, for λ = 0 and 1, respectively. This means that both cases are compatible with β ∼ 1/2, and that SSR processes converge equally fast toward their limiting distributions as pure random walks do.