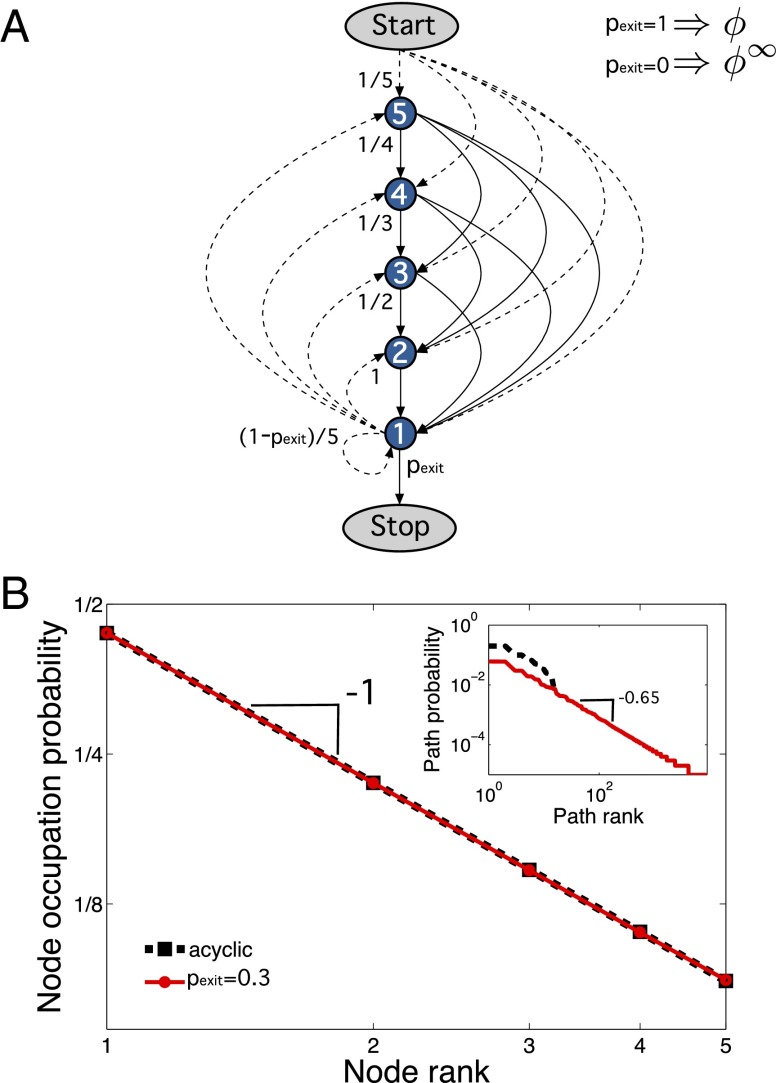
Fig. 5.

(A) SSR processes seen as random walks on networks. A random walker starts at the start node and diffuses through the directed network. Depending on the value of $p_{\text{exit}}$, two possible types of walks are possible. For $p_{\text{exit}}=1$, the finite ($2^{N-1}=16$ possible paths) and acyclic process ϕ is recovered that stops after a single path; for $p_{\text{exit}}=0$, we have the infinite and cyclical process, ${\varphi }^{\infty }$. For $p_{\text{exit}}>0$ we have the mixed process, ${\Phi }^{\text{mix}}=p_{\text{exit}}\varphi +\left(1-p_{\text{exit}}\right){\varphi }^{\infty }$. (B) The occupation probability for ${\Phi }^{\text{mix}}$ is unaffected by the value of $p_{\text{exit}}$. The repeated ϕ (dashed black line) and the mixed process with $p_{\text{exit}}=0.3$ (solid red line) have exactly the same occupation probability $p_N\left(i\right)$, which corresponds to the stationary visiting distribution of nodes in the ${\varphi }^{\infty }$ network by random walkers. (Inset) Rank distribution of path-visit frequencies. Clearly they depend strongly on $p_{\text{exit}}$. Whereas the acyclic ϕ produces a finite distribution, the cyclic one produces a power law, matching the theoretical prediction of ref. 27. For the simulation we generated $5\cdot {10}^5$ sequence samples and found $\mathrm{32,523}$ distinct sequences for $p_{\text{exit}}=0.3$.