Towards Drug Repositioning: A Unified Computational Framework for Integrating Multiple Aspects of Drug Similarity and Disease Similarity

Abstract

In response to the high cost and high risk associated with traditional de novo drug discovery, investigation of potential additional uses for existing drugs, also known as drug repositioning, has attracted increasing attention from both the pharmaceutical industry and the research community. In this paper, we propose a unified computational framework, called DDR, to predict novel drug-disease associations. DDR formulates the task of hypothesis generation for drug repositioning as a constrained nonlinear optimization problem. It utilizes multiple drug similarity networks, multiple disease similarity networks, and known drug-disease associations to explore potential new associations among drugs and diseases with no known links. A large-scale study was conducted using 799 drugs against 719 diseases. Experimental results demonstrated the effectiveness of the approach. In addition, DDR ranked drug and disease information sources based on their contributions to the prediction, thus paving the way for prioritizing multiple data sources and building more reliable drug repositioning models. Particularly, some of our novel predictions of drug-disease associations were supported by clinical trials databases, showing that DDR could serve as a useful tool in drug discovery to efficiently identify potential novel uses for existing drugs.

Introduction

The inefficiency of pharmaceutical drug development with high expenditure but low productivity has been widely discussed^1,2. Drug repositioning, the process of finding additional indications (i.e., diseases) for existing drugs, presents a promising avenue for identifying better and safer treatments without the full cost or time required for de novo drug development. Candidates for repositioning are usually either market drugs or drugs that have been discontinued in clinical trials for reasons other than safety concerns. Because the safety profiles of these drugs are known, clinical trials for alternative indications are cheaper, potentially faster and carry less risk than de novo drug development. Any newly identified indications can be quickly evaluated from phase II clinical trials. Drug repositioning can reduce drug discovery and development time from 10–17 years to potentially 3–12 years³. Therefore, it is not surprising that in recent years, new indications, new formulations, and new combinations of previously marketed products accounted for more than 30% of the new medicines that reach their first markets⁴. Drug repositioning has drawn widespread attention from the pharmaceutical industry, government agencies, and academic institutes. However, current successes in drug repositioning have primarily been the result of serendipitous events based on ad hoc clinical observation, unfocused screening, and “happy accidents”. Comprehensive and rational approaches are urgently needed to explore repositioning opportunities.

A reasonable systematic method for drug repositioning is the application of phenotypic screens by testing compounds with biomedical and cellular assays. However, this method also requires additional wet bench work of developing appropriate screening assays for each disease being investigated, and it thus remains challenging in terms of cost and efficiency. Big data analytics for both drugs and diseases provide an unprecedented opportunity to uncover novel statistical associations between drugs and diseases in a scalable manner. Many computational methods have been developed in this direction, including: (1) matching drug indications by their disease-specific response profiles based on the Connectivity Map (CMap) data^5,6; (2) predicting novel associations between drugs and diseases by the “Guilt by Association” (GBA) approach⁷; (3) utilizing structural features of compounds/proteins to predict new targets or indications, such as molecular docking^8,9, and quantitative structure-activity relationship (QSAR) modelling¹⁰; (4) identifying associations between drugs and diseases in genetic activities, such as genome-wide association study (GWAS)¹¹, pathway profiles¹², and transcriptional responses¹³; (5) constructing drug network and using network neighbors to infer novel drug uses based on phenotypic profiles, such as side effects^14–16, and gene expression^17,18. All of these methods only focus on different aspects of drug/disease activities and therefore result in biases in their predictions. Also, these methods suffer from the noise in the given information source. Recently, several integrative methods which combine chemical, genetic, or phenotypic features were proposed to predict drug indications, for example, PREDICT¹⁹, SLAMS²⁰, PreDR²¹, Li and Lu²², Huang et al²³, and Napolitano et al²⁴.

In this paper, we propose a unified computational framework for drug repositioning hypothesis generation, by integrating multiple Drug information sources and multiple Disease information sources to facilitate drug Repositioning tasks (DDR). DDR utilizes drug similarity network, disease similarity network, and known drugdisease associations to explore the potential associations among other unlinked drugs and diseases. In the experiment, we investigate three types of drug information (i.e., chemical structure, target protein, and side effect) and three types of disease information (i.e., phenotype, ontology, and disease gene). The proposed framework is also extensible, and thus DDR can incorporate additional types of drug/disease information sources.

Compared to prior integrative drug repositioning methods, it is worthwhile to highlight the following novel aspects that DDR can achieve simultaneously: (1) DDR can predict additional drug-disease associations by considering both drug information and disease information. With the exception of PREDICT¹⁹, which integrates drug similarity scores and disease similarity scores using unweighted geometric mean, other integrative methods only consider either some drug information sources or some disease information sources. (2) DDR can determine interpretable importance of different information sources during the prediction. To our knowledge ours is the first study to do so. (3) As by-products, DDR can also discover the drug and disease groups, such that the drugs or diseases within the same group are highly correlated with each other, thus providing additional insights for targeted downstream investigations including clinical trials.

Construction of Drug Similarity and Disease Similarity Measures

In this section we introduce drug/disease similarities to quantify the degree of sharing common characteristics between pairs of drugs/diseases. A drug/disease similarity provided for a pair of drugs/diseases is a score that ranges from 0 to 1, with 0 representing the lowest similarity and 1 standing for the highest similarity. For each drug pair, we calculated three types of similarities based on chemical structures, target proteins, and side effects. For each disease pair, we calculated three types of similarities based on disease phenotypes, disease ontology, and disease genes.

Drug Similarity of Chemical Structures D^chem

It is generally believed that drugs with similar chemical structures would carry out common therapeutic function, thus likely treat common diseases. We calculated the first drug pairwise similarity based on a chemical structure fingerprint corresponding to the 881 chemical substructures²⁵ defined in PubChem database²⁶. Each drug d was represented by an 881-dimensional binary profile h(d) whose elements encode for the presence or absence of each PubChem substructure by 1 or 0, respectively. Then the pairwise chemical similarity between two drugs d and d′ is computed as the Tanimoto coefficient of their chemical fingerprints:

$$D_{d,d^{\prime }}^{chem}=\frac{h(d)·h(d^{\prime })}{|h(d)|+|h(d^{\prime })|-h(d)·h(d^{\prime })}$$ (1)

where |h(d)| and |h(d′)| are the counts of substructure fragments in drugs d and d′ respectively. The dot product h(d)•h(d′) represents the number of substructure fragments shared by two drugs.

Drug Similarity of Target Proteins D^target

A drug target is the protein in the human body whose activity is modified by a drug resulting in a desirable therapeutic effect. Drugs sharing common targets often possess similar therapeutic function. We collected all target proteins for each drug from DrugBank²⁷. Then we calculated the pairwise drug target similarity between drugs d and d′ based on the average of sequence similarities of their target protein sets:

$$D_{d,d^{\prime }}^{\text{target}}=\frac{1}{|P(d)||P(d^{\prime })|}{\displaystyle \sum _{i=1}^{|P(d)|}{\displaystyle \sum _{j=1}^{|P(d^{\prime })|}SW(P_i(d),P_j(d^{\prime }))}}$$ (2)

where given a drug d, we presented its target protein set as P(d); then |P(d)| is the size of the target protein set of drug d. The sequence similarity function of two proteins SW was calculated as a Smith-Waterman sequence alignment score²⁸.

Drug Similarity of Side Effects D^se

Drug side effects, or adverse drug reactions, indicate the malfunction by off-targets. Thus side effects are useful to infer whether two drugs share similar target proteins and treat similar diseases. We obtained side effect keywords from SIDER²⁹, an online database containing drug side effect information extracted from package inserts using text mining methods. Each drug d was represented by 4192-dimensional binary side effect profile e(d) whose elements encode for the presence or absence of each of the side effect key words by 1 or 0 respectively. Then the pairwise side effect similarity between two drugs d and d′ is computed as the Tanimoto coefficient of their side effect profiles:

$$D_{d,d^{\prime }}^{se}=\frac{e(d)·e(d^{\prime })}{|e(d)|+|e(d^{\prime })|-e(d)·e(d^{\prime })}$$ (3)

where |e(d)| and |e(d′)| are the counts of side effect keywords for drugs d and d′ respectively. The dot product e(d)•e(d′) represents the number of side effects shared by two drugs.

Disease Similarity of Phenotypes S^pheno

Disease phenotypes indicate phenotypic abnormalities encountered in human diseases. We used the phenotypic similarity constructed by van Driel et al³⁰. The disease phenotypic similarity was constructed by identifying similarity between the MeSH terms³¹ appearing in the medical description (“full text” and “clinical synopsis” fields) of diseases from OMIM database³². To be specific, each disease s in OMIM was represented by K-dimensional (K is the number of the MeSH terms) MeSH term feature vector m(s): each entry in the feature vector represents an MeSH term, and the counts of the term found for disease s are the corresponding feature value. Then the pairwise disease phenotype similarity between two diseases s and s′ is computed as the cosine of the angle between their feature vectors:

$$S_{s{s}^{\prime }}^{pheno}=\frac{{\displaystyle {\sum }_{i=1}^{K}m{(s)}_{i}m{(s^{\prime })}_i}}{\sqrt{{\displaystyle {\sum }_{i=1}^K{m}^2{(s)}_i}}\sqrt{{\displaystyle {\sum }_{i=1}^K{m}^2{(s^{\prime })}_i}}}$$ (4)

where m(s)_i denotes the i-th entry of the feature vector m(s).

Disease Similarity of Disease Ontology S^do

The Disease Ontology (DO)³³ is an open source ontological description of human disease, organized from a clinical perspective of disease etiology and location. The terms in DO are disease names or disease-related concepts and are organized in a directed acyclic graph (DAG). Two linked diseases in DO are in an “is-a” relationship, which means one disease is a subtype of the other linked disease. And the lower a disease is in the DO hierarchy, the more specific the disease term is. We calculated the semantic similarity between any pair of the diseases using the tool DOSim³⁴. For a disease term s in DO, the probability that the term is used in disease annotations is estimated as p_s, which is the number of disease term s or its descendants in DO divided by the total number of disease terms in DO. Then the semantic similarity of two diseases s and s′ is defined as the information content of their lowest common ancestor by:

$$S_{s{s}^{\prime }}^{do}=-\log \underset{x\in C(s,s^{\prime })}{\min }{p}_x$$ (5)

where C(s,s′) is the set of all common ancestors of diseases s and s′.

Disease Similarity of Disease Genes S^gene

Disease-causing aberrations in the normal function of a gene define that gene as a disease gene. We collected all disease genes for each disease from “phenotype-gene relationships” field from OMIM database. Then we calculated the pairwise disease similarity between diseases s and s′ based on the average of sequence similarities of their disease gene sets:

$$S_{s{s}^{\prime }}^{gene}=\frac{1}{|G(s)||G(s^{\prime })|}{\displaystyle \sum _{i=1}^{|G(s)|}{\displaystyle \sum _{j=1}^{|G(s^{\prime })|}SW(G_i(s),G_j(s^{\prime }))}}$$ (6)

where given a disease s, we presented its disease gene set as G(s); then |G(s)| is the size of the disease gene set of disease s. The sequence similarity function of two disease genes SW was calculated as a Smith-Waterman sequence alignment score.

Methodology

In this section we present the details of the proposed DDR approach. Suppose we have n information sources to measure drug similarity and m information sources to measure disease similarity. Let D_k∈ℝ^n×n be the drug similarity matrix measured on the k-th information source, and suppose there are in total K_d information sources to measure the drug similarities. Similarly, let S_l∈ℝ^m×m be the disease similarity matrix measured on the l-th information source and suppose there are K_s sources to measure the disease similarities. Let U∈ℝ^n×C_D be the latent drug grouping matrix with C_D the number of drug groups, and U_ij indicates the possibility that the i-th drug belonging to the j-th drug cluster. V∈ℝ^m×C_S be the latent disease grouping matrix with C_S the number of disease groups, and V_ij indicating the possibility that the i-th disease belonging to the j-th disease cluster. R∈ℝ^n×m be the observed (i.e., known) drug-disease association matrix with R_ij=1 if the association between the i-th drug and j-th disease is observed, and R_ij=0 otherwise. Then we aim to analyze the drug-disease network by minimizing the following objective:

$$J=J_0+{\lambda }_1{J}_1+{\lambda }_2{J}_2$$ (7)

where the three parts in the objective are:

• The reconstruction loss of observed drug-disease associations:

  $$J_0=\Vert \Theta -U\Lambda V^T{\Vert }^{2}F$$ (8)

  Here Θ∈ℝ^n×m is the estimated dense version of R, and Λ∈ℝ^C_D^×C_S encodes the relationship between drug clusters and disease clusters.
• The reconstruction loss of drug similarities:

  $$J_1={{\displaystyle {\sum }_{k=1}^{K_d}\omega }}_k\Vert D_k-U{U}^T{\Vert }_F^2+{\delta }_1\Vert \omega {\Vert }_2^2$$ (9)

  Here the estimated drug similarity matrix is UU^T, and ω∈ℝ^K_d^×1 is the nonnegative weight vector when aggregating the reconstruction loss on different drug information sources. The L₂ norm regularization is added to avoid trivial solution³⁵ and δ₁≥0 is the tradeoff parameter.
• The reconstruction loss of disease similarities:

  $$J_2={{\displaystyle {\sum }_{l=1}^{K_s}\pi }}_l\Vert S_l-V{V}^T{\Vert }_F^2+{\delta }_2\Vert \pi {\Vert }_2^2$$ (10)

  Here the estimated disease similarity matrix is VV^T, and π∈ℝ^K_s^×1 is the nonnegative weight vector when aggregating the reconstruction loss on different disease information sources. The L₂ norm regularization is added for the same reasons in equation (9).

Putting everything together, we obtained the optimization problem to be resolved:

$$\begin{array}{c}{\min }_{\mathrm{U}}{}_{,\mathrm{V},\Lambda ,\Theta ,\omega ,\pi }J\\ \text{subject to}U\ge 0,V\ge 0,\Lambda \ge 0,\omega \ge 0,{\omega }^{\mathrm{T}}1=1,{\pi }^{\mathrm{T}}1=1,{\mathrm{P}}_{\Omega }(\Theta )={\mathrm{P}}_{\Omega }(R)\end{array}$$ (11)

where Ω is the set of indices of the observed associations, and P_Ω is the projection operator on obtaining the entries of a matrix indexed by the indices in Ω. Thus the constraint P_Ω(Θ)= P_Ω(R) restricts the estimated drug-disease associations should include the ones that are already observed. Note that to enhance the interpretability of the learned model, we require U, V, and Λ to be nonnegative, ω and π to be in simplexes. As there are lots of symbols and notations involved in problem (11), we summarize them in Table 1. To further help understanding those symbols as well as their roles in problem (11), we also provide a graphical illustration of the main idea of DDR in Figure 1.

Table 1.

Notations and symbols of the methodology

Notation	Size	Meaning
Dk	n×n	The k-th drug similarity matrix
Sl	m×m	The l-th disease similarity matrix
U	n×CD	Drug cluster assignment matrix
V	m×CS	Disease cluster assignment matrix
Λ	CD×CS	Drug-disease cluster relationship matrix
R	n×m	Observed drug-disease association matrix
Θ	n×m	Densified estimation of R
ω	Kd×1	Drug similarity weight vector
π	Ks×1	Disease similarity weight vector

Figure 1.

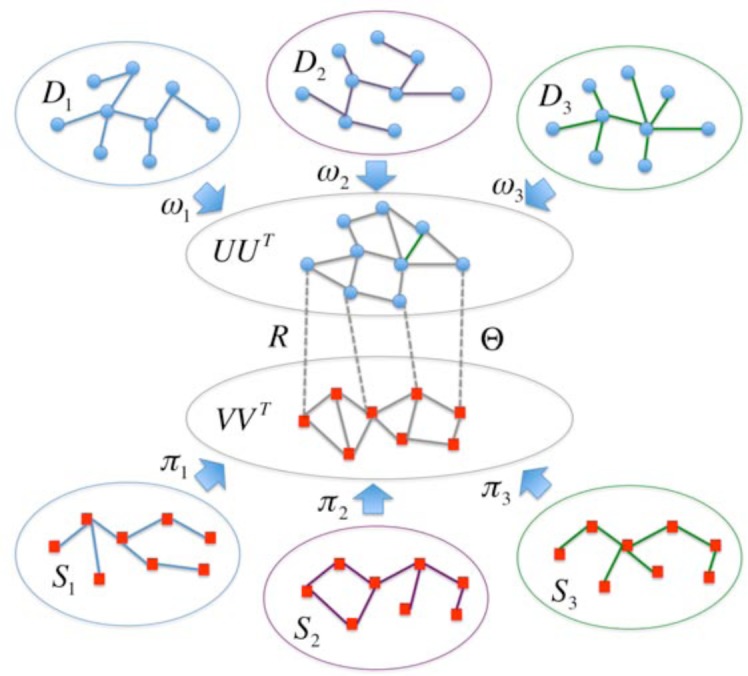
A graphical illustration of the main idea of DDR. There are multiple information sources that we can utilize to construct drug/disease similarities, and the constructed drug/disease similarity matrices are denoted by ${\left\{D_k\right\}}_{k=1}^{K_d}\text{or}{(S_l)}_{l=1}^{K_s}$. There is also an observed drug-disease association matrix R. Then DDR can learn the drug/disease grouping matrix U or V, the estimated drug-disease association matrix Θ and the importance of different drug/disease information sources ω or π.

Our proposed DDR method integrates multiple drug similarities, multiple disease similarities, and known drug-disease associations to achieve a global estimation on the entire drug-disease network including the intrinsic drug similarity, intrinsic disease similarity, as well as drug-disease associations. DDR formulates such a network estimation problem as a constrained nonlinear optimization problem. Since there are multiple groups of variables involved in the optimization problem (11), we adopt an efficient solution based on the Block Coordinate Descent (BCD) strategy³⁶. The BCD approach works by solving the different groups of variables alternatively until convergence. At each iteration, it solves the optimization problem with respect to one group of variables with all other groups of variables fixed. Due to lack of space, details of the BCD solution procedure and its complexity analysis is provided at http://astro.temple.edu/~tua87106/ddr_bcd.pdf.

Results and Discussion

In this section we present experimental evaluation results of the proposed DDR algorithm on a drug repositioning task.

Data Description

The benchmark dataset, which is used to test the performance of DDR using a community standard, was extracted from NDF-RT³⁷ by Li and Lu²². It spans 3,250 treatment associations between 799 drugs and 719 diseases. We considered drug information from three data sources: chemical structure, target protein, and side effect. Thus, three 799×799 matrices were used to represent drug similarities between 799 drugs from different perspectives. Similarly, we considered disease information from three data sources: disease phenotype, disease ontology, and disease gene. Thus, three 719×719 matrices were used to represent disease similarities between 719 human diseases from different perspectives. The presence or absence of known associations between drug and disease was denoted by 1 or 0 respectively. Thus, a 799×719 matrix R used to represent the known drug-disease associations. We plotted the statistic of the known drug-disease associations in Figure 2. In that dataset, most of drugs (75%) treat <5 diseases; 18% of drugs treat 5 to 10 diseases; only 7% of drugs treat >10 diseases (Figure 2(a)). Although the disease hypertension has 78 related drugs, 80% of diseases have only <5 drugs; 10% of diseases have 5–10 drugs; and remaining 10% of diseases have >10 drugs.

Figure 2.

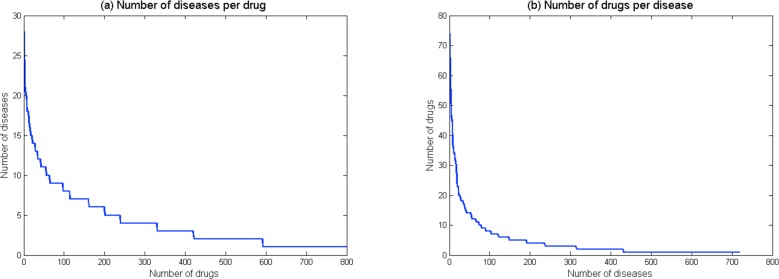
Statistics of the known drug-disease association dataset. (a) The number of indicated diseases per drug. (b) The number of drugs per disease.

Method Comparison

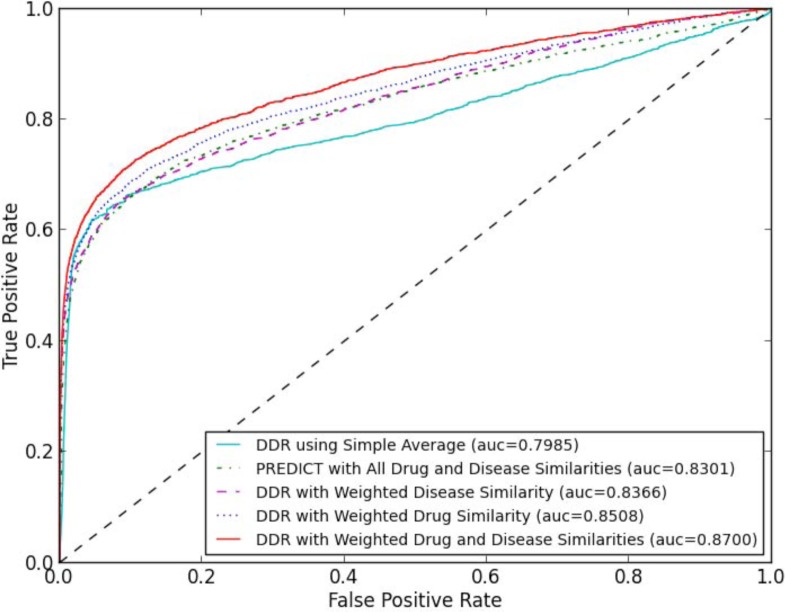
We used a 10-fold cross-validation scheme to evaluate drug repositioning approaches. To ensure the validity of the test cases, we held out all the associations involved with 10% of the drugs in each fold, rather than holding out associations directly. To obtain robust results, we performed 50 independent cross-validation runs, in each of which a different random partition of dataset to 10 parts was used. In our comparisons, we considered five drug repositioning methods: (1) DDR using Simple Average. The method only considers reconstruction loss of observed drug-disease associations (i.e., J₀ of objective formula (7) in the methodology section), and assumes each drug/disease source is equally informative. Thus the method uses the average of drug/disease similarity matrices as the integrated drug/disease similarity. (2) DDR with Weighted Drug Similarity. The method considers reconstruction losses of observed drug-disease associations and drug similarities (i.e., J₀ and J₁ in objective formula (7)). The method uses the average of disease similarity matrices as integrated disease similarity, and automatically learns drug similarity weight vector (ω) based on the contributions of drug information sources to the prediction. (3) DDR with Weighted Disease Similarity. The method considers reconstruction losses of observed drug-disease associations and disease similarities (i.e., J₀ and J₂ in objective formula (7)). The method uses the average of drug similarity matrices as integrated drug similarity, and automatically learns disease similarity weight vector (π) based on the contributions of disease information sources to the prediction. (4) DDR with Weighted Drug and Disease Similarities. The method considers all reconstruction losses proposed in the paper (i.e., formula (7) as a whole). The method automatically learns drug similarity weight vector (ω) and disease similarity weight vector (π) together based on the contributions of drug and disease information sources to the prediction. (5) PREDICT with All Drug and Disease Similarities. To our knowledge, PREDICT¹⁹ is the only other method could consider both drug and disease information sources. PREDICT uses unweighted geometric mean of pairs of drug-drug and disease-disease similarity measures to construct classification features and subsequently learns a logistic regression classifier that distinguishes between true and false drug-disease associations. PREDICT could not provide weight for each drug/disease information source. Figure 3 shows the averaged ROC curves of 50 runs of the cross-validation for different methods based on the experiment.

Figure 3.

The averaged ROC comparison of five drug repositioning approaches generated from 50 runs of 10-fold cross-validation. Methods are sorted in legend of the figure according to their AUC score.

Figure 3 shows that our proposed DDR framework is effective for drug repositioning tasks. Without considering reconstruction loss of any similarity measure, DDR using Simple Average obtains an averaged AUC score of 0.7985. When considering weighted drug similarity (i.e., reconstruction loss of drug similarities) or weighted disease similarity (i.e., reconstruction loss of disease similarities), DDRs obtain averaged AUC scores of 0.8508 or 0.8366 respectively. In the experiment, drug-based optimization (i.e., DDR with Weighted Drug Similarity) obtains a higher AUC score than disease-based optimization (i.e., DDR with Weighted Disease Similarity). This could be partially explained with the following reason. The 799 drugs we studied are marketed medications, which usually have rich and precise pharmacological data; thus drug-based optimization might be preferred in this case. For novel drugs or clinical candidates, disease-based optimization might be preferred to overcome missing knowledge in the pharmacology of a drug³⁸ (e.g., additional targets, unknown side effect). When considering weighted drug similarity and weighted disease similarity together, DDR obtain the highest averaged AUC score (0.8700). The observation indicates that drug-based optimization and disease-based optimization could be complementary, and computational drug repositioning tasks should optimize both drug similarity and disease similarity. Another observation is PREDICT with All Drug and Disease Similarities obtains an averaged AUC score of 0.8301. Although PREDICT considers drug/disease similarity and utilizes a logistic regression to weigh classification features, the result indicates that their strategy of feature construction (assembles all possible combinations of drug/disease similarity measures together as classification features) is less accurate than DDR.

One “bonus” characteristic of DDR is it provides interpretable importance of different information sources based on their contributions to the prediction. The i-th element of drug/disease weight vector ω/π corresponds to the i-th drug/disease data sources. Since we constrained ω/π to be in a simplex in problem formula (11), the sum of all elements of ω/π is 1. Obtained from DDR with Weighted Drug and Disease Similarities, the averaged DDR weights of each data source and their standard deviations during the cross-validation experiments are plotted in Figure 4. For drug data sources, chemical structure obtains averaged weight of 0.2744, target protein obtains averaged weight of 0.2295, and side effect obtains a much higher averaged weight of 0.4961 (Figure 4(a)). This could be partially explained with the following reasons. Chemical structure and target protein sources focus on drug’s molecular mechanism of action (MOA) from a genotypic perspective. However, the pre-clinical outcomes based on MOA often do not correlate well with therapeutic efficacy in drug development. It is estimated that of all compounds effective in cell assays, only 30% of them could work in animals. Even worse, only 5% of them could work in humans³⁹. Side effects are generated when drugs bind to off-targets, which perturb unexpected metabolic or signaling pathways. For marketed drugs, which have relatively complete side effect profiles, side effect information from clinical patients may be seen as valuable read-outs of drug effects directly on human bodies⁴⁰ (i.e., with less translational problems). Thus, side effects could server as a promising perspective for drug repositioning. For disease data sources, phenotype obtains averaged weight of 0.4248, disease ontology obtains averaged weight of 0.3958, and disease gene obtains a lower averaged weight of 0.1794 (Figure 4(b)). The lower weight of disease gene data source may be due to the fact that the gap between phenotype (human disease) and genotype (human gene) is too large⁴¹, and the known associations between diseases and genes (obtained from OMIM) are incomplete.

Figure 4.

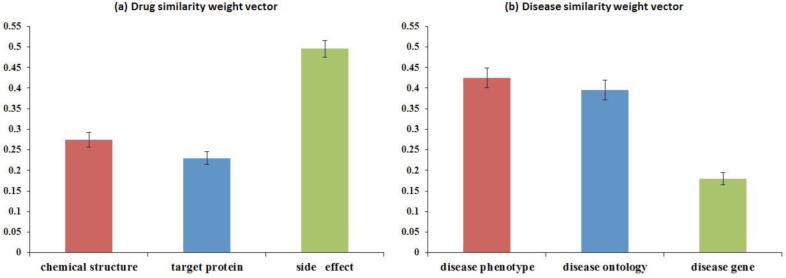
Distribution of averaged weights and standard deviations of the similarity weight vectors obtained by DDR. (a) Drug similarity weight vector ω contains weights of chemical structure, target protein, and side effect data sources. (b) Disease similarity weight vector π contains weights of disease phenotype, disease ontology, and disease gene sources.

Novel Predictions and Case Studies

We performed an additional leave-disease-out experiment to demonstrate the capability of DDR on uncovering drug-disease associations and predicting novel drug candidates for each disease. To ensure the validity of the test cases, we held out all the known drug-disease associations with the tested disease. The validation setting mimics a real-world setting: once rare/unknown diseases without any treatment information arise, a computational drug repositioning method should provide potential drugs based on characteristics (e.g. phenotypes, related genes) of the new diseases and the existing drug/disease similarities. In the experiment, we alternatively leave each disease i out and ran DDR (considered weighted drug and disease similarities). More specifically, we set all elements in i-th column of matrix R to 0, and used this R along with drug/disease similarity matrices as inputs of DDR. Then we used i-th column of the densified estimated matrix Θ as the drug prediction scores for the disease i. In this way, we got prediction scores for all possible associations between the 799 drugs and 719 diseases.

As an example, treatment predictions for Alzheimer’s disease (AD) were analyzed. For the six drugs which are known to treat AD, DDR assigned scores of 0.7091 to Selegiline, 0.6745 to Valproic Acid, 0.6348 to Galantamine, 0.5675 to Donepezil, 0.5571 to Tacrine, and 0.5233 to Rivastigmine, which are significantly larger than those of the other 793 drugs (mean and standard deviation are 0.1565±0.1628). Table 2(a) shows the top 10 drugs predicted for AD by our DDR approach. Of the 10 drugs, only three (Selegiline, Valproic Acid, and Galantamine) appear in our known drug-disease association list. The remaining 7 predicted drugs (along with other high-ranked ones in the leave-disease-out experiment) could be considered as drug repositioning candidates for AD. Some predictions are explainable and supported by clinical evidence from ClinicalTrials.gov (i.e., pharmaceutical investigators have been aware of the associations, which are still in the experimental stages). Metformin, a drug commonly used to treat type II diabetes, can help trigger the pathway used to instruct stem cells in the brain to become neural cells⁴². Clinical trial NCT01965756 is under way to evaluate Metformin as a potential therapy for AD. Bexarotene, a skin cancer drug (for cutaneous T-cell lymphoma) that rapidly removed the damaging protein implicated in the progression of the illness from the brains of mice⁴³, has been tested to treat AD in recent clinical trials (NCT01782742 and NCT02061878). Nilvadipine, a calcium channel blocker (CCB) for treatment of hypertension, also blocks the production of amyloid proteins linked to AD⁴⁴. Nilvadipine has been tested in a clinical trial as a possible treatment for AD in Ireland (NCT02017340).

Table 2.

Top 10 drugs for diseases Alzheimer’s Disease (AD) and Systemic Lupus Erythematosus (SLE) based on DDR predictions

(a) Top 10 drugs predicted for AD			(b) Top 10 drugs predicted for SLE
Drug	Prediction Score	Clinical Evidence?	Drug	Prediction Score	Clinical Evidence?
Selegiline*	0.7091	—	Desoximetasone	0.7409	No
Carbidopa	0.6924	No	Azathioprine*	0.7269	—
Amantadine	0.6897	No	Leflunomide	0.7078	Yes
Procyclidine	0.6826	No	Fluorometholone	0.7054	No
Valproic Acid*	0.6745	—	Triamcinolone*	0.6862	—
Metformin	0.6543	Yes	Beclomethasone	0.6522	No
Bexarotene	0.6426	Yes	Etodolac	0.6445	No
Neostigmine	0.6385	No	Hydroxychloroquine*	0.6374	—
Galantamine*	0.6348	—	Nelfinavir	0.6371	Yes
Nilvadipine	0.6159	Yes	Mercaptopurine	0.6150	No

^*denotes the drug is known and approved to treat the disease

Another example we analyzed is treatment predictions for Systemic Lupus Erythematosus (SLE). For the three drugs which are known to treat SLE, DDR assigned scores of 0.7269 to Azathioprine, 0.6862 to Triamcinolone, and 0.6374 to Hydroxychloroquine, which are significantly larger than those of the other 796 drugs (mean and standard deviation are 0.1707±0.1617). Table 2(b) shows the top 10 drugs predicted for SLE by our DDR approach. The top 10 predictions include all the three known treatments to SLE, which shows the effectiveness of our method. The remaining 7 predicted drugs (along with other high-ranked ones in the leave-disease-out experiment) could be considered as drug repositioning candidates for SLE. Some predictions are explainable and supported by clinical evidence from ClinicalTrials.gov. Leflunomide, a pyrimidine synthesis inhibitor, is used to treat moderate to severe rheumatoid arthritis and psoriatic arthritis. A genetic link study shows rheumatoid arthritis and SLE sufferers share a variant of the same STAT4 gene, and therapies developed to treat one disease may possibly be able to treat the other⁴⁵. Therefore, it is not surprising to see Leflunomide is tested as a treatment for SLE in a clinical trial (NCT00637819). Nelfinavir, one of the protease inhibitors, has been approved for use in the treatment of human immunodeficiency virus (HIV). Protease inhibitors have been shown to interfere with binding of anti-double stranded DNA antibodies to their targets (some bindings may lead to organ damage) and may decrease inflammation in SLE⁴⁶. Recently, a clinical trial (NCT02066311) has been proposed to evaluate Nelfinavir as a potential therapy for SLE.

Conclusion

We have proposed a general computational framework, called DDR, to explore drug-disease association for drug repurposing hypothesis generation. Our method takes into consideration multiple drug similarities, multiple disease similarities, and known drug-disease associations, to uncover the potential additional associations among other unlinked drugs and diseases. Experimental results demonstrate the effectiveness of the proposed method, and suggest that our method could help identify drug repositioning opportunities, which will benefit patients by offering more effective and safer treatments.