Pediatric Readmission Classification Using Stacked Regularized Logistic Regression Models

Abstract

Background:

Regulations and privacy concerns often hinder exchange of healthcare data between hospitals or other healthcare providers. Sharing predictive models built on original data and averaging their results offers an alternative to more efficient prediction of outcomes on new cases. Although one can choose from many techniques to combine outputs from different predictive models, it is difficult to find studies that try to interpret the results obtained from ensemble-learning methods.

Methods:

We propose a novel approach to classification based on models from different hospitals that allows a high level of performance along with comprehensibility of obtained results. Our approach is based on regularized sparse regression models in two hierarchical levels and exploits the interpretability of obtained regression coefficients to rank the contribution of hospitals in terms of outcome prediction.

Results:

The proposed approach was used to predict the 30-days all-cause readmissions for pediatric patients in 54 Californian hospitals. Using repeated holdout evaluation, including more than 60,000 hospital discharge records, we compared the proposed approach to alternative approaches. The performance of two-level classification model was measured using the Area Under the ROC Curve (AUC) with an additional evaluation that uncovered the importance and contribution of each single data source (i.e. hospital) to the final result. The results for the best distributed model (AUC=0.787, 95% CI: 0.780–0.794) demonstrate no significant difference in terms of AUC performance when compared to a single elastic net model built on all available data (AUC=0.789, 95% CI: 0.781–0.796).

Conclusions:

This paper presents a novel approach to improved classification with shared predictive models for environments where centralized collection of data is not possible. The significant improvements in classification performance and interpretability of results demonstrate the effectiveness of our approach.

Introduction

The widespread use and availability of Electronic Health Record (EHR) data are responsible for numerous studies and should result in measurable improvements of the healthcare quality level in the coming years. However, most of the available data from healthcare repositories nowadays are still very limited in terms of heterogeneity and most studies use local data repositories [1, 2]. The Health Information Technology for Economic and Clinical Health HITECH act of 2009 was one of the most recent incentives of the US government to establish healthcare data exchange systems. However, in many cases legal and privacy concerns is still the main reason against data exchange between hospitals or healthcare providers [3]. On the other hand, researchers are often faced with a complex task of data integration even in cases where an agreement for data integration is reached [4]. On the other hand, one can observe a growing number of studies that use millions of records to build predictive models that will be used on the future repositories of EHRs [5–7].

Multiple privacy-preserving distributed classification models with applications in healthcare were proposed recently. Mathew and Obradovic [8] proposed a distributed knowledge-mining framework based on a decision tree classifier. Their approach allows heterogeneous data schemas to build a decision tree using locally abstracted data – i.e. no raw data needs to leave the hospital. Another distributed approach was proposed in [9] where distributed distance metric learning was used to assess patient similarity. A recent approach by Wang et al. [10] used a Bayesian approach to online learning based on logistic regression. High-level privacy preserving was ensured by encrypted posterior distribution of coefficients during the exchange between the server and the client. Additionally, the proposed model supports asynchronous communication between hospitals and allows dynamic model updating – i.e. there is no need to rebuild the model for each new patient. However, the complexity of the proposed approach rises with the number of included hospitals and [10] only presents results with up to 8 hospitals contributing to the global logistic regression model. Rider and Chawla [11] use probabilistic graphical models to facilitate transfer learning between distinct healthcare data sets by parameter sharing while simultaneously constructing a disease network for interpretation by domain experts. Their approach is primarily used to rank the patient disease risk for multiple diseases simultaneously. A recent study by Wiens et al. [12] presents a more empirical evaluation of a transfer-learning approach using data from multiple hospitals to enhance local hospital predictions. A large sample of 132,853 admissions from three hospitals was used to test different scenarios on sharing the data or using models built on data from a specific hospital to predict on data from other participating hospitals. Although the study does not address privacy directly, it offers interesting results demonstrating high performance gains when data from all hospitals can be used in the final prediction.

Our study utilizes a large dataset of hospital discharge data to propose a novel approach in distributed predictive modeling that allows asynchronous exchange of models in a peer-to-peer or centralized environment. The proposed predictive model consists of two levels and is based on deep learning architectures [13, 14] that originate from a stacked generalization approach [15]. It was evaluated using data from 54 hospitals in California to demonstrate the large-scale deployment possibilities of the proposed approach. Compared to similar frameworks, we allow an additional high-level interpretability of results to obtain additional hospital level information. In contrast to most related work our approach allows combinations of different predictive models.

Background

Beginning October 1, 2012 under section 3025 of the Affordable Care Act, hospital reimbursements became tied to performance relative to preventable 30-day Medicare hospital readmission rates compared with hospitals having similar predicted risk profiles. Initially, readmission rates are tracked for three specific adult diagnoses: acute myocardial infarction (MI), congestive heart failure (HF), and pneumonia (PN). This change in the structure of Medicare reimbursements places increasing importance on the ability of health care providers to identify predictors of 30-day hospital readmissions as well as to identify characteristics of individuals and providers associated with above-average levels of readmission risk. Under-performing hospitals will see reduction of up to 1% in Medicare base reimbursements for services related to all diagnostic-related groups (DRGs). In 2010, these targets would have placed half of all hospitals in the under-performing group.

There are now plans to expand this approach to consider pediatric populations and growing interest in considering the value of pediatric readmissions rates as hospital quality indicators [16–18]. Research on pediatric readmission rates suggests that a small number of cases account for a disproportionate number of hospital readmissions [19]. Similarly, wide hospital-level variation is also seen. Considering sickle-cell anemia readmissions in a sample of more than 12,000 hospitalizations of some 4,762 children from 33 hospitals, Sobota et al. [20] found that even after adjusting for individual-level characteristics such as age, treatment, and complications, there was 4.2-fold variation in readmission rates between hospitals. Considering only admissions for appendicitis, Rice-Townsend et al. [21] found 3.8-fold variation between hospitals in readmissions rates after adjusting for disease severity and insurance status. In a larger study including 568,845 all-cause admissions at 72 children’s hospitals, Berry et al. [22] found 28.6% greater adjusted readmission rates in hospitals with high versus low readmission rates. Overall, these findings point to the importance of considering differences between hospitals.

Despite considerable interest in this topic, the accuracy of predictive models for 30-day hospital readmission is not particularly strong. Horwitz et al. [23], for example, found in-sample prediction by area under the curve (AUC) of 0.61, 0.63, and 0.61 for MI, HF, and PN, respectively using Medicare claims data. More recently, focusing only on MI readmissions, Krumholz et al. [24] used 2006 Medicare claims data to compare models relying on claims data versus the combination of claims data and medical record data. These authors found high agreement (r=.98), but their overall model had an AUC of just 0.63.

Methods

Combining outputs of different predictive models to improve the performance of classification has been widely addressed in the research literature for the past two decades. The simplest approach to combining predictions from different models is majority voting, also called bagging [25] when combined with bootstrap sampling from the training dataset. In cases where classifiers are built from disjoint sets of data, Ting and Witten [26] name the approach “dagging.” In the same paper they propose an approach called dag-stacking, where an additional model is built to combine the outputs of low-level models instead of majority voting.

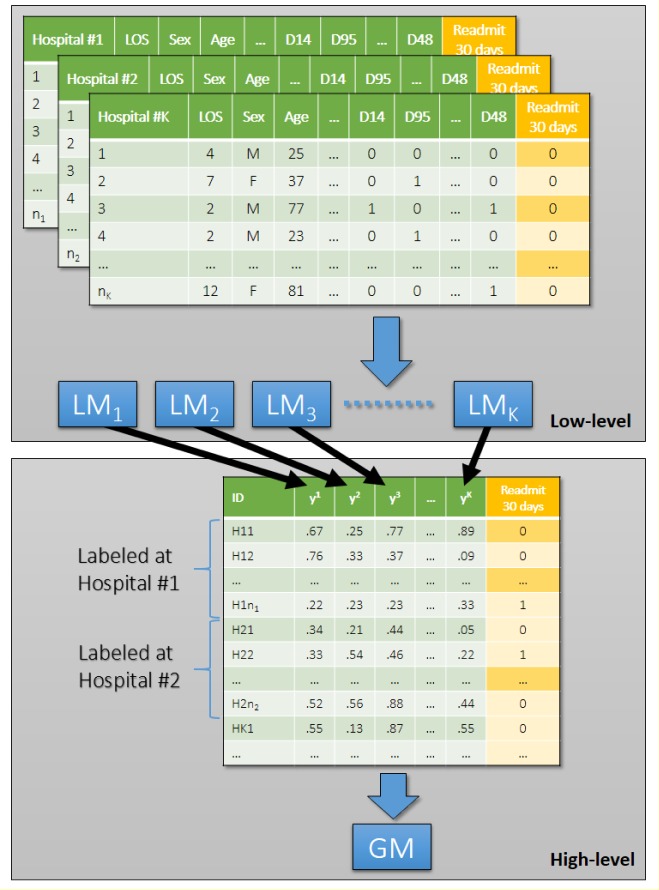
Stacked generalization approach inspired many novel, so-called deep learning frameworks [13, 14]. This paper introduces a stacked generalization based classification approach, inspired by dag-stacking, with a few important modifications from the original implementation by Wolpert [15] and Ting and Witten [26]. As described above, stacked generalization was originally proposed to leverage different types of classifiers that are used on the lower level of the stacking framework using a high-level classifier. Our approach aims to combine different classifiers of the same type built on disjoint sets of data (i.e. each classifier is built on data from a specific hospital). Ting and Witten [27] already noticed that it is possible to improve the results of the originally proposed stacking framework by combining confidence levels in contrast to predicted class labels. In our case, we use predicted risk of readmission obtained from regularized logistic regression models to prepare a high-level dataset (Figure 1). Additionally, we use a high level classifier (i.e. sparse logistic regression) that allows us to interpret the results of the high level classifier.

Figure 1.

Two-level classification framework for distributed hospital based predictive modeling.

Suppose we have K different clinical sites or hospitals, on each site k there are n_k patients characterized by a matrix $X_k={\left[x_1^k,x_2^k,\dots ,x^{{}^k{n}_k}\right]}^T$. We construct a local model f_k : R^d → R at each site k such that $f_k(x_i^k)$ returns the probability of hospital readmission for the i^th patient in the k^th clinical site, d is the dimensionality of the patient feature vector. For example, in the case of logistic regression, it learns a linear decision function

$$f_k(x_i^k)=w_k^T{x}_i^k+b_k$$

by minimizing the following logistic loss

$${\ell }_{org}^k(w_k,b_k)=\frac{1}{n}{\displaystyle \sum _{i=1}^{{}^{n}k}\log }\left[1+\exp \left(-y_i^k\left(w_k^T{x}_i^k+b_k\right)\right)\right]$$

where $y_i^k\in \{0,1\}$ is the label of $x_i^k$, such that $y_i^k=1$ if the i^th patient in the k^th clinical site is re-admitted to hospital within 30 days, and $b_k\in R$ is the offset. The optimal solution of (w_k, b_k) by minimizing ${\ell }_{org}^k(w_k,b_k)$ can be obtained by iterative optimization methods such as gradient descent, Newtown method, or coordinate descent. For a detailed comparison of those methods one can refer to [28].

Generally there are many factors involved in every patient during the predictive modeling procedure, which makes d fairly large. In most of the cases only a small portion of factors would play important roles. It is highly desirable if the prediction model can also identify the set of important factors. Therefore Sparse Logistic Regression model is proposed, which aims to get the optimal (w_k, b_k) by minimizing the following objective

$${\ell }_{sp}^k(w_k,b_k)=\frac{1}{n}{\displaystyle \sum _{i=1}^{{}^{n}k}\log }\left[1+\exp \left(-y_i^k\left(w_k^T{x}_i^k+b_k\right)\right)\right]+\lambda {\Vert w_k\Vert }_1$$

where λ > 0 is the parameter trading off model sparsity and accuracy, and ||•||₁ is the vector ℓ₁ norm. The objective can be minimized by accelerated gradient descent as described in [29]. However, simple ℓ₁ regression has some limitations in small sample high dimensional case, as well as in the case when there are a group of highly correlated variables.

To overcome these limitations, Zou et al. [30] proposed elastic net regularization, which solves the optimal (w_k, b_k) by minimizing the following objective

$${\ell }_{enet}^k(w_k,b_k)=\frac{1}{n}{\displaystyle \sum _{i=1}^{{}^{n}k}\log }\left[1+\exp \left(-y_i^k\left(w_k^T{x}_i^k+b_k\right)\right)\right]+{\lambda }_1{\Vert w_k\Vert }_1+{\lambda }_2{\Vert w_k\Vert }_2$$

where λ₂ > 0 is a regularization parameter and ||•|| is the ℓ₂ norm of a vector.

With this formulation, we can get the objective of original logistic regression with λ₁ = λ₂ = 0, sparse logistic regression with λ₂ = 0, and ridge logistic regression with λ₁ = 0. ${\ell }_{enet}^k(w_k,b_k)$ can be minimized by existing software packages such as Glmnet [31]. If $(w_k^{*},b_k^{*})$ is the optimal solution, then the probability that the i^th patient in the k^th clinical site is re-admitted to hospital within 30 days can be computed as

$$p(y_k^i=1|x_k^i)=\frac{1}{1+\exp \left[-(w_k^T{x}_k^i+b_k)\right]}$$

After we got the optimal prediction model $f_k^{*}(1\le k\le K)$ for each site k, we collect all those models and form a set

$$F^{*}=\{f_1^{*},f_2^{*},\dots ,f_K^{*}\}$$

Those models will be used as the low-level models. Then for each patient vector x ∈ R^d, we can form a K-dimensional vector

$$F^{*}(x)={\left[f_1^{*}(x),f_2^{*}(x),\dots ,f_K^{*}(x)\right]}^T$$

We can train another prediction model g : R^K → R on those K-dimensional vectors, which will be used as the decision function on the higher level. Finally, we stack F and g together to make a classification decision.

Results

This section introduces the experimental settings of all experiments, followed by experimental results and interpretation of the high-level model to demonstrate the effectiveness of the proposed approach.

Experimental Settings

Hospital discharge data from California, State Inpatient Databases (SID), Healthcare Cost and Utilization Project (HCUP), Agency for Healthcare Research and Quality [32] was used in all experiments. The SID is a component of the HCUP, a partnership between federal and state governments and industry, tracking all hospital admissions at the individual level. We used all data from January 2009 through December 2011 in the pre-processing phase. Pediatric patients up to 10 years of age were used in this study due to specific regulations that allow age reporting in months instead of years only for patients younger than 132 months. Patients were excluded from the analysis if they died prior to discharge, were discharged on the same day as admission, were transferred to another institution, or were missing data on the unique patient identifier, age or sex. After pre-processing, we obtained the final dataset containing 66,994 discharge records with 11,184 positive (readmitted within 30 days) and 55,810 negative records.

The bottom 80% of all ICD-9-CM diagnosis codes, ranked by observed frequency, were removed from the dataset, leaving the top 122 diagnosis codes as binary diagnosis features. An additional 21 features (e.g., sex, age, month of admission, length of stay, total charges in USD, etc.) were also included (Table 1). Log transformed values for three numerical features (age, length of stay and total charges in USD) were also included. By recoding nominal features to binary values, we obtained 185 features that were used to build the models presented below.

Table 1.

List of 143 features used for building and testing the proposed predictive models.

Feature name	Description	Feature name	Description
DSHOSPID	Unique hospital identifier	PAY1	Primary payer
TOTCHG	Total charge in USD	MEDINCSTQ	Quartile classification of the patient’s estimated median household income
AGEMONTH	Age in months (12 – 131)	ASCHED	Scheduled hospitalization
LOS	Length of stay in days	PL_UR_CAT4	Four category urban-rural designation for the patient’s county of residence
TOTCHG_LOG	Log transformed total charge in USD	Race	Race and ethnicity (White, Black, Hispanic, Asian or Pacific Islander, Native American, Other)
NPR	Number of procedures on hospital discharge record	MDC	Major Diagnostic Category
NCHRONIC	Number of chronic conditions	ORPROC	Operating room procedures
LOS_LOG	Log transformed length of stay	NECODE	Number of ICD9 E codes
ASOURCE	Source of admission	TRANIN	Type of admission
HCUP_ED	Presence of emergency department codes	HospitalUnit	Six hospital unit categories
FEMALE	Identification of gender	D1 – D122	Binary variables for presence of the most frequent diagnoses
Feature name	Description	Feature name	Description
DSHOSPID	Unique hospital identifier	PAY1	Primary payer
TOTCHG	Total charge in USD	MEDINCSTQ	Quartile classification of the patient’s estimated median household income
AGEMONTH	Age in months (12 – 131)	ASCHED	Scheduled hospitalization
LOS	Length of stay in days	PL_UR_CAT4	Four category urban-rural designation for the patient’s county of residence
TOTCHG_LOG	Log transformed total charge in USD	Race	Race and ethnicity (White, Black, Hispanic, Asian or Pacific Islander, Native American, Other)
NPR	Number of procedures on hospital discharge record	MDC	Major Diagnostic Category
NCHRONIC	Number of chronic conditions	ORPROC	Operating room procedures
LOS_LOG	Log transformed length of stay	NECODE	Number of ICD9 E codes
ASOURCE	Source of admission	TRANIN	Type of admission
HCUP_ED	Presence of emergency department codes	HospitalUnit	Six hospital unit categories
FEMALE	Identification of gender	D1 – D122	Binary variables for presence of the most frequent diagnoses

Each experimental run included randomized training and test dataset where 2/3 of samples were used for training and 1/3 for testing. The holdout testing could cause extremely low number of positive cases in smaller hospitals. Therefore, we removed all records belonging to hospitals with less than 150 records. After removal of records from smaller hospitals, we obtained a final dataset with 61,111 records (10,675 positive and 50,436 negative). Due to a large number non-pediatric hospitals, only 54 out of the initial 205 hospitals were retained for the experiments. The test dataset was not used at all during the process of stacking or model development.

Classification Performance

To evaluate the performance of the built classifiers, we used Area under ROC Curve (AUC) metric. Holdout testing was repeated 1000 times to obtain more robust comparison of the AUC scores. In each run, we calculated the results for the following classification approaches:

• - Best performing local model (BLM),

• - Simple averaging of the local model outputs (AVG),

• - Two-level deep learning architecture (DLA),

• - Advanced two-level deep learning architecture with two different local models per hospital - i.e. elastic net and generalized boosted regression models [33] (DLA2) and

• - Global sparse logistic regression model (elastic net) built on data from all hospitals. Figure 2 presents the distribution of AUC results for the three compared approaches (SLRA).

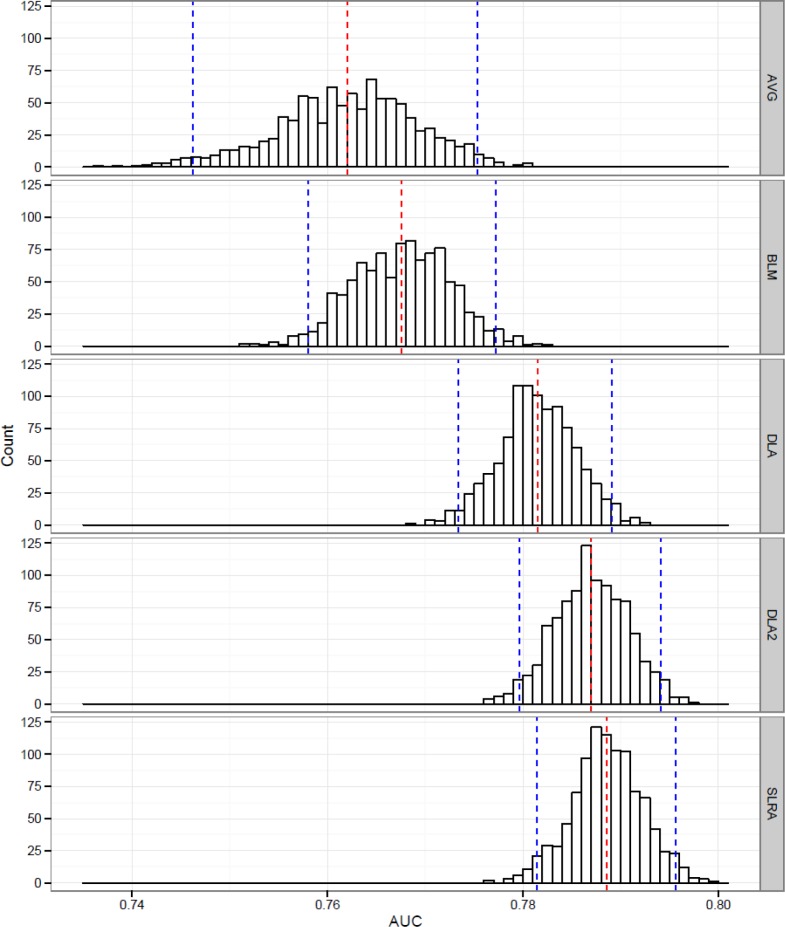
Figure 2.

Distribution of AUC results on 1000 hold-out runs for averaged local models (AVG), best local model (BLM), deep learning approach (DLA), deep learning approach with two classifiers (DLA2) and single sparse logistic regression on all samples (SLRA) with mean AUC (red dotted line) and 95% CI (blue dotted line).

It can be observed that plain deep learning approach (AUC=0.781, 95% CI: 0.773–0.789) with a single elastic net classifier on hospital level does not significantly outperform a simple averaging approach (AUC=0.762, 95% CI: 0.746–0.775). However, it does perform much better on average. The proposed approach is also better in comparison to the best performing model from a single hospital (AUC=0.768, 95% CI: 0.758–0.777). We also observed the performance of the weakest local classifiers with an average AUC of 0.416 (95% CI: 0.355–0.481). These results point out that there are hospitals with models that cannot be used for practical application and would gain significantly if they can evaluate the risk for their patients with the proposed approach. When we added an additional, conceptually different model (i.e. generalized boosted models), for each hospital, in DLA2 (AUC=0.787, 95% CI: 0.780–0.794) we were able to significantly outperform AVG and BLM.

We were also interested in how much performance is lost when we compare our approach to a global model that would use all available data (simulating a scenario with no data exchange restrictions between hospitals). It turns out that neither DLA nor DLA2 significantly differ in terms of AUC performance when compared to single elastic net model built on all available data (AUC=0.789, 95% CI:0.781–0.796). On the other hand, both DLA2 and SLRA significantly outperformed averaged and best single models from hospitals.

Interpretation of the High-level Classifier Results

In contrast to proposed approaches in distributed learning for medical applications [8–12], our approach additionally allows healthcare experts to interpret the results of the high-level classifier. The only constraint is the comprehensibility of the high-level classifier. In case of sparse logistic regression, we can obtain important information on inclusion of the local hospital models in the global model. Nevertheless, this is not the only information we can obtain – one can observe the relative influence of the specific local models in the global solution. For further interpretation of the global regression model, we calculated relative influence of all 54 local models based on their inclusion in the global model in 1000 holdout runs. Relative Hospital Influence (RHI) was calculated as a percentage of holdout runs when the specific hospital was included in the high-level sparse logistic regression model (i.e. hospital’s coefficient was non-zero). Table 2 demonstrates high level of heterogeneity among hospitals.

Table 2.

Descriptive overview for 54 hospitals included in the study.

	Min	Max	Median	Mean	SD
Number of records	151	7,884	346.5	1,130.82	1,747.32
Average length of stay	1.90	12.68	3.42	3.95	1.79
Average number of chronic diseases	0.32	3.88	1.50	1.60	0.85
Average total charge (in USD)*	6,615	123,700	32,410	38,230	28,333
Average age of children (in months)	34.76	115.50	55.56	56.97	16.12

^*12 hospitals with missing total charge data were excluded

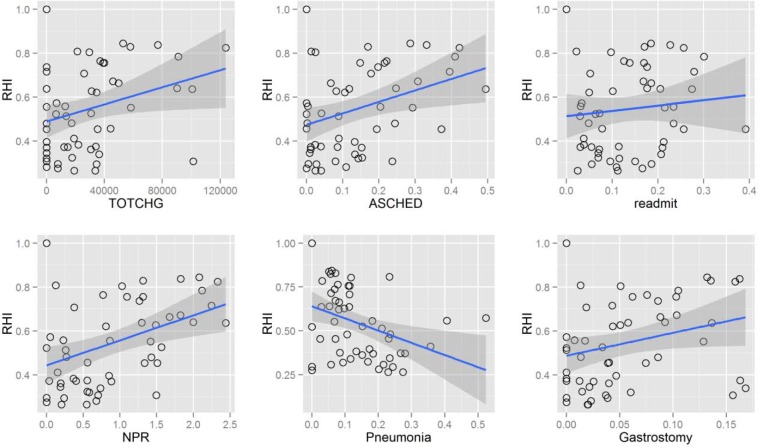
Figure 3 presents correlation of RHI with the most interesting patient characteristics averaged for each of 54 hospitals that were selected based on their increasing or decreasing temporal trend. It can be observed that hospitals with higher cost per patient (TOTCHG) on average contribute more influential models to the final solution. There could be multiple reasons for correlation of influence and cost per patient (larger sample size in such hospitals, specialization of hospitals treating complex conditions, etc.). Therefore, some further analysis would be needed to explain this correlation. Likewise, average number of procedures on patient’s discharge records correlates with RHI. This correlation is not difficult to explain as more procedures on the discharge records also means more details for the classification algorithm that can be used. Another positive correlation – i.e. with the average percentage of scheduled patients can be observed in the left lower chart of Figure 3. One should conduct further research into characteristics of hospitals where a large proportion of admission are scheduled to explain this correlation. The only negative correlation presented is the one relating RHI with percentage of children with pneumonia. It turns out that the high-level classifier rarely used outputs from hospitals with lower percentage of pneumonia. It is known from previous studies [34] that prediction of 30-day readmission represents a difficult problem with AUC performance of 0.63. Therefore, it might be possible that models from hospitals with high percentage of pneumonia perform relatively weak and are therefore rarely selected for inclusion in the final model. Readmission rates for hospitals also correlate with the RHI, pointing out that models built on data with stronger class imbalance will have a lower probability of inclusion. The last chart in lower right corner of Figure 3 presents another positive correlation between percentage of patients with gastrostomy (one of the most prevalent diagnoses in the observed population) and RHI. Berry et al. [22] found a similar relation in a study on recurrent readmission within children hospitals, where they confirmed a correlation between readmission frequency and the percentage of technology assistance. The most prevalent technologies among the patients with four or more readmissions were digestive related (30.7%), including gastrostomy tube.

Figure 3.

Trends of Relative Hospital Influence (RHI) in relation to average total charge per hospital (TOTCHG), percentage of records with diagnosed pneumonia (Pneumonia), average number of procedure codes on the record (NPR), rate of 30-day readmissions (readmit), percentage of scheduled admissions (ASCHED) and percentage of records with gastrostomy (Gastrostomy).

Conclusions

In this study, we present a novel approach to distributed predictive modeling with application to 30-day all-cause readmission in children hospitals. Our approach is based on stacked generalization, dag-stacking and recently proposed deep-learning architectures. Using the proposed approach it is possible to significantly outperform a simple averaging as well as the best performing models from single hospitals. The results demonstrate that there is no significant difference in terms of AUC performance between the global model where data from all hospitals can be used and our approach to distributed predictive modeling. Additionally, our proposed models can be interpreted on high-level, offering an additional insight into the characteristics of specific hospitals. As such, the additional information can be used on policy-making levels to observe hospital quality on a more global level.