Estimating Effective Population Size from Temporally Spaced Samples with a Novel, Efficient Maximum-Likelihood Algorithm

Abstract

The effective population size $N_{\text{e}}$ is a key parameter in population genetics and evolutionary biology, as it quantifies the expected distribution of changes in allele frequency due to genetic drift. Several methods of estimating $N_{\text{e}}$ have been described, the most direct of which uses allele frequencies measured at two or more time points. A new likelihood-based estimator $\widehat{N_{\text{B}}}$ for contemporary effective population size using temporal data is developed in this article. The existing likelihood methods are computationally intensive and unable to handle the case when the underlying $N_{\text{e}}$ is large. This article tries to work around this problem by using a hidden Markov algorithm and applying continuous approximations to allele frequencies and transition probabilities. Extensive simulations are run to evaluate the performance of the proposed estimator $\widehat{N_{\text{B}}}$, and the results show that it is more accurate and has lower variance than previous methods. The new estimator also reduces the computational time by at least 1000-fold and relaxes the upper bound of $N_{\text{e}}$ to several million, hence allowing the estimation of larger $N_{\text{e}}$. Finally, we demonstrate how this algorithm can cope with nonconstant $N_{\text{e}}$ scenarios and be used as a likelihood-ratio test to test for the equality of $N_{\text{e}}$ throughout the sampling horizon. An R package “NB” is now available for download to implement the method described in this article.

THE effective size of a population is a key concept in population genetics that links together such seemingly disparate quantities as the equilibrium levels of genetic variation and linkage disequilibrium, the size of temporal changes in allele frequencies, the probability of fixation of a new mutation, and others (Charlesworth and Charlesworth 2010). Often $N_{\text{e}}$ is estimated from information on mutation rates and standing levels of nucleotide variation (Charlesworth 2009). In most species there is some level of population differentiation (i.e., individuals from geographically distant areas are more genetically different than those from the same location), and in this case standing levels of genetic variation within a local population give estimates of the effective population size summed across all subpopulations of the species (Charlesworth and Charlesworth 2010). Standing levels of variation also reflect effective population sizes over many thousands or millions of generations.

For some purposes it is more interesting to estimate the current (or recent) size of a local subpopulation. In these circumstances it is common to use fluctuations in allele frequencies over multiple generations to estimate $N_{\text{e}}$, with larger fluctuations indicating a smaller variance effective population size (Krimbas and Tsakas 1971; Waples 1989). This follows from the fact that the variance of genetic drift experienced in a population is a function of $N_{\text{e}}$ and can be quantified under the Wright–Fisher model. The variance of genetic drift in one generation is $p(1-p)/(2N_{\text{e}})$ for a diploid population with effective population size $N_{\text{e}}$ and initial allele frequency p [for haploid populations, $p(1-p)/N_{\text{e}}$]. Hence it is possible to estimate the effective population size of a closed population by investigating the magnitude of temporal changes in allele frequencies.

One approach to estimating $N_{\text{e}}$ from temporal samples is to use F-statistics (Krimbas and Tsakas 1971; Nei and Tajima 1981; Pollak 1983; Waples 1989; Jorde and Ryman 2007). F-statistics can be obtained by calculating the standardized variance of gene frequency change, after sampling error is taken into consideration. The F-statistics are moment-based estimators, making them easy to compute. They tend to be slightly biased upward in general and suffer from large bias when rare alleles are used (Waples 1989; Wang 2001).

Another class of temporal estimators uses the likelihood approach. Williamson and Slatkin (1999) proposed the full-likelihood approach in estimating $N_{\text{e}}$ (see also Anderson et al. 2000; Wang 2001; Berthier et al. 2002). There are several advantages of using maximum likelihood over the F-statistics. For example, the maximum-likelihood estimator has a lower variance and smaller bias, resulting in more precise estimates (Williamson and Slatkin 1999; Wang 2001). It also allows a more flexible sampling scheme, that allele frequency data can be collected from more than two time points. On the downside, the likelihood methods are computationally demanding compared to the F-statistics, because they make use of the full distributional information of the allele frequency across generations. Numerical maximization of the likelihood function is usually involved, and the associated computational difficulties increase with more loci and longer sampling horizons. As a result, the likelihood methods are not suitable for populations with large $N_{\text{e}}$. The $N_{\text{e}}$ used in previous simulation studies were limited to between 20 and 100 diploid individuals only (Williamson and Slatkin 1999; Anderson et al. 2000; Wang 2001; Berthier et al. 2002).

It is unfortunate that computing difficulties limit the use of the current likelihood approaches, despite their precision and rigorous statistical basis. Waples (1989) and Pollak (1983) both commented that indirect (genetic) methods for estimating $N_{\text{e}}$ are necessary only if $N_{\text{e}}$ is large, but this is precisely the case in which the temporal methods are less reliable. This study aims to provide an alternative likelihood-based estimator that solves the problems in the current likelihood methods. Therefore the new estimator should (1) be computationally compact, (2) be able to work with a wide range of $N_{\text{e}}$, and (3) be mostly unbiased and have at least the same degree of precision as the other methods.

Theory

The full-likelihood model and MLNE

The full-likelihood model was developed by Williamson and Slatkin (1999) and is used as the basic model in this article. The full-likelihood function for two samples is

$$\begin{array}{l}L\left(N_{\text{e}}\right)=f\left(x_0,x_t|N_{\text{e}}\right)\\ ={\displaystyle {\sum }_{p_0,p_t}f\left(x_0|p_0\right)f\left(x_t|p_t\right)f\left(p_t|p_0,N_{\text{e}}\right)f\left(p_0|N_{\text{e}}\right)}\end{array}$$ (1)

(Williamson and Slatkin 1999, equation 4), where $x_0, x_t$ are the sampled allele counts and $p_0,p_t$ are the underlying true allele frequencies. For sampling, it is assumed that the samples are taken with replacement; hence $f\left(x_0|p_0\right)$ and $f\left(x_t|p_t\right)$ are binomially and independently distributed with n being the number of sampled diploid individuals:

$$f\left(x_i|p_i\right)=\frac{2n!}{x_i!\left(2n-x_i\right)!}{p}_i^{x_i}{\left(1-p_i\right)}^{2n-x_i},\hspace{1em}\text{for}\hspace{0.5em}i=0,t.$$ (2)

The probability $f\left(p_t|p_0, N_{\text{e}}\right)$ is calculated using the forward transition matrix M. Each element of M, ${\left\{m\right\}}_{ij}$, is the probability of the population drifting from the state having i copies to j copies of an allele. Under the Wright–Fisher model, the transition matrix for biallelic loci can be obtained from a binomial distribution. As the possible number of alleles runs from 0 to $2N_{\text{e}}$, the dimension of the transition matrix M is $\left(2N_{\text{e}}+1\right)\times (2N_{\text{e}}+1)$. Clearly a computational issue arises here. For a moderately large $N_{\text{e}}$, say $N_{\text{e}}=10,000$, the dimension of the transition matrix becomes 20,001² (which is ∼400 million), and this is the number of transition probabilities that needs to be calculated to fill in the matrix M. Furthermore, if the two samples were taken from t generations apart, M has to be multiplied by itself t times to get the transition probabilities for t generations ahead. For large $N_{\text{e}}$ it may not be feasible to compute every element in the matrix M and multiply a matrix of such a size, even with the advance of computing power.

For the likelihood function itself, $p_0$ and $p_t$ are nuisance (unobserved, latent state) parameters that need to be marginalized out by summing over all possible combinations of $p_0$ and $p_t$. For more than two samples, the likelihood function becomes

$$\begin{array}{c}L\left(N_{\text{e}}\right)=f\left( x_0,x_1,\dots ,x_t|N_{\text{e}}\right)\\ ={\displaystyle {\sum }_{p_0,p_1,\dots ,p_t}\left[\begin{array}{l}f\left(x_0|p_0\right)f\left(x_1|p_1\right)\dots f\left(x_t|p_t\right)\hfill \\ \times f\left(p_t|p_{t-1}\right)\dots f\left(p_1|p_0,N_{\text{e}}\right)f\left(p_0|N_{\text{e}}\right)\hfill \end{array}\right]}\end{array}$$ (3)

(Williamson and Slatkin 1999, equation 6), where $p_0, p_1, \dots , p_t$ are the underlying true allele frequencies and treated as nuisance parameters. To marginalize out the underlying allele frequencies, we need to sum over all possible values of $p_0, p_1, \dots , p_t$, and the number of summations equals the number of nuisance parameters. Closed-form expressions of the summations may not exist, and they are calculated numerically in this case. Although the form of the likelihood function is explicit, it is computationally intensive to evaluate and maximize it.

While no software appears to be available for the full-likelihood model, the software package MLNE was created to implement the pseudolikelihood approach proposed by Wang (2001) and Wang and Whitlock (2003). The pseudolikelihood omits some of the insignificant transition probabilities in the matrix M and hence reduces computational effort. However, it is still computationally demanding and the computation time increases rapidly with increasing $N_{\text{e}}$ (Wang 2001). Currently, the upper bound for $N_{\text{e}}$ that MLNE can handle is ∼38,000 on a 64-bit Windows machine with 16 GB of memory.

A continuous approximation

While the Wright–Fisher model assumes discrete allele frequencies, Fisher (1922) first applied differential equations to model the dynamics of allele frequencies over time. Kimura (1955) derived the complete solution of the differential equation, using the method of moments. The core assumption of the continuous approximation is that $N_{\text{e}}$ is sufficiently large that the moments of the continuous distribution converge to the exact moments. To visualize the model, the process can be represented as a hidden Markov model (Figure 1) (a similar diagram appeared in Anderson et al. 2000). Here $p_0,\dots , p_t$ are the underlying true allele frequencies according to the Wright–Fisher model, and $x_0,\dots , x_t$ are observations from the system. We define $x_0,\dots , x_t$ as allele counts; hence they are positive integers running from $0, \dots , 2n$ (assuming the species is diploid). We aim to derive the joint relationship among all the observations $x_0,\dots , x_t$ and then infer the parameter $N_{\text{e}}$ governing the process. We investigate the components in this likelihood and hence derive our estimator $\widehat{N_{\text{B}}}$. As with the Wright–Fisher model, this model also assumes nonoverlapping generations, an isolated population, and constant effective population size $N_{\text{e}}$. Other genetic forces including selection and mutation are assumed to be insignificant relative to genetic drift (Waples 1989; Williamson and Slatkin 1999; Wang 2001).

Figure 1.

Hidden Markov model representing the structure of the process. $p_0,\dots , p_t$ is the sequence of true allele frequencies propagating according to the Wright–Fisher model but they are unobserved. $x_0,\dots , x_t$ are the realizations or the sampled allele frequencies.

Two samples:

In the two-sample model, we assume only two samples $x_0, x_t$ are obtained. In a later section the model is extended to handle multiple sampling events. The likelihood function is the joint density of our two observations $x_0$ and $x_t$ is

$$L\left(N_{\text{e}}\right)=f\left(x_t,x_0|N_{\text{e}}\right)=f\left(x_t|x_0,N_{\text{e}}\right)f(x_0).$$ (4)

This is the simplest form of the likelihood function for our parameter of interest $N_{\text{e}}$, given our observed values. We can see that $x_0$ is the initial observed allele count and has no relationship with $N_{\text{e}}$. Therefore $f(x_0)$ does not play a role in maximizing the likelihood and can be treated as a constant. We can then rewrite the likelihood function as follows:

$$L(N_{\text{e}})\propto f(x_t|x_0,N_{\text{e}}).$$ (5)

By considering the unobserved nuisance parameters, the likelihood function becomes

$$\begin{array}{c}L\left(N_{\text{e}}\right)\propto f\left(x_t|x_0,N_{\text{e}}\right)\\ ={\displaystyle {\int }_0^1{\displaystyle {\int }_0^{1}f\left(x_t|p_t\right)f\left(p_t|p_0,N_{\text{e}}\right)f\left(p_0|x_0\right)}d{p}_{t}d{p}_0}.\end{array}$$ (6)

Equation 6 is the continuous analogy of Equation 1, with summations being replaced by integrals. The terms of the likelihood function have the same meaning as in Equation 1: $f(x_t|p_t)$ is the sampling allele counts at generation t, $f\left(p_t|p_0, N_{\text{e}}\right)$ is the transition probability that plays the same role as the Wright–Fisher matrix in the full-likelihood model, and the last term $f\left(p_0|x_0\right)$ is the distribution of initial allele frequency conditioning on the initial observation. The integrals are to “sum over” all possible values of the underlying allele frequencies. In the following paragraphs we evaluate each part of the likelihood function and finally derive the general formula for the likelihood function.

The starting allele frequency is unknown in general. We may assume $p_0$ is uniformly distributed [equivalent to $\text{beta}(1, 1)]$ before any observations are taken, because it brings no additional parameters to the system (Williamson and Slatkin 1999). If $x_0$ is sampled binomially from $p_0$ under Equation 2, then by Bayes’ rule, the conditional distribution of $p_0|x_0$ follows a beta distribution (e.g., chap. 7.2.3 in Casella and Berger 2002):

$$f\left(p_0|x_0\right)=\frac{f\left(x_0|p_0\right)f(p_0)}{{{\displaystyle \int }}_0^{1}f\left(x_0|p_0\right)f\left(p_0\right)d{p}_0}\sim \text{beta}(x_0+1,2n-x_0+1).$$ (7)

In fact, $f\left(p_0|x_0\right)$ has the same role as $f\left(x_0|p_0\right)f\left(p_0|N_{\text{e}}\right)$ in the full-likelihood model in Equation 1.

Next, for the transition probability $f\left(p_t|p_0,N_{\text{e}}\right)$, a continuous distribution is used to model allele frequency instead of the discrete transition matrix in the full-likelihood model. The probability density function of $p_t$ given $p_0$ under genetic drift is

$$f\left(p_t|p_0,N_{\text{e}}\right)\sim \text{beta}\left(\delta p_0, \delta \left(1-p_0\right)\right) ,$$ (8)

where δ is called the “drift parameter” that controls the amount of drift:

$$\delta =\frac{{\left(1-1/2N_{\text{e}}\right)}^t}{1-{\left(1-1/2N_{\text{e}}\right)}^t}.$$ (9)

The drift parameter is a function of $N_{\text{e}}$ and the sampling interval t. It is derived from the continuous model of genetic drift by Kimura (1955) for sufficiently large $N_{\text{e}}$ and is a popular method to model the change in allele frequency due to genetic drift (Kitakado et al. 2006; Song et al. 2006). For the special case of $t=1$, δ reduces to $2N_{\text{e}}-1.$

After obtaining the formulas for $f\left(p_0|x_0\right)$ and $f\left(p_t|p_0, N_{\text{e}}\right)$, the integral with respect to $p_0$ in the likelihood function (Equation 6) can be calculated in advance. Let us rewrite the likelihood function:

$$L\left(N_{\text{e}}\right)\propto {\displaystyle {\int }_0^{1}f\left(x_t|p_t\right)}\left[{\displaystyle {\int }_0^{1}f\left(p_t|p_0,N_{\text{e}}\right)f\left(p_0|x_0\right)d{p}_0}\right]d{p}_t.$$ (10)

The inner integral forms a hierarchical process that $p_0$ is distributed as beta given the initial observation $x_0$ and $p_t$ also follows another beta distribution conditioning on $p_0$. An exact solution may not exist for this type of integral. Here we propose to use another beta distribution to approximate the integral. The parameters in this new beta distribution can be obtained by matching the first two moments:

$$\begin{array}{l}{\displaystyle {\int }_0^{1}f\left(p_t|p_0,N_{\text{e}}\right)f\left(p_0|x_0\right)d{p}_0}\\ \approx \text{beta}\left({\alpha }^{\prime }=\frac{\delta \left(x_0+1\right)}{2n+2+\delta },{\beta }^{\prime }=\frac{\delta \left(2n-x_0+1\right)}{2n+2+\delta }\right).\end{array}$$ (11)

The goodness of fit of this approximation is examined in the Appendix.

The final piece of the likelihood function is $f\left(x_t|p_t\right)$, which is the sampling allele count given the underlying true allele frequency $p_t$. If the samples are taken with replacement, then it is binomially distributed as described in Equation 2. Now, putting all the elements together, the likelihood function becomes

$$\begin{array}{c}L\left(N_{\text{e}}\right)\propto f\left(x_t|x_0\right)\\ ={\displaystyle {\int }_0^{1}f\left(x_t|p_t\right)f\left(p_t|x_0,N_{\text{e}}\right)d{p}_t}\\ ={\displaystyle {\int }_0^1\frac{2n!}{x_t!\left(2n-x_t\right)!}{p}_t^{x_t}{\left(1-p_t\right)}^{2n-x_t}}\\ \times \frac{1}{B\left({\alpha }^{\prime },{\beta }^{\prime }\right)}{p}_t^{{\alpha }^{\prime }-1}{\left(1-p_t\right)}^{{\beta }^{\prime }-1}d{p}_t\\ =\frac{2n!}{x_t!\left(2n-x_t\right)!}\frac{1}{B\left({\alpha }^{\prime },{\beta }^{\prime }\right)}{\displaystyle {\int }_0^1{p}_t^{x_t+{\alpha }^{\prime }-1}{\left(1-p_t\right)}^{2n-x_t+{\beta }^{\prime }-1}d{p}_t}\\ =\frac{2n!}{x_t!\left(2n-x_t\right)!}\frac{B\left(x_t+{\alpha }^{\prime },2n-x_t+{\beta }^{\prime }\right)}{B\left({\alpha }^{\prime },{\beta }^{\prime }\right)},\end{array}$$ (12)

where $B()$ is a beta function. This integral has a closed-form solution with $f\left(p_t|x_0, N_{\text{e}}\right)$ being a beta distribution and the binomial sampling of $f\left(x_t|p_t\right)$. The resultant probability mass function is a beta-binomial distribution with three parameters: $2n,{\alpha }^{\prime },and{\beta }^{\prime }$. We can see from Equations 10 and 12 that the integrals (which play the same role as the summations in the full-likelihood model) can be evaluated separately with either a closed-form expression or an approximate solution, yielding a much simplified likelihood. The relationship between the two samples $x_0$ and $x_t$ is now established through a beta-binomial distribution. We define $\widehat{N_{\text{B}}}$ as the value of $N_{\text{e}}$ at which the likelihood function attains its maximum, conditioning on the observations. Hence $\widehat{N_{\text{B}}}$ is the maximum-likelihood estimator (MLE) of the parameter $N_{\text{e}}$. For many unlinked loci, the joint likelihood is calculated as the product of each of the individual likelihoods for the loci.

Three or more samples

The likelihood model can be extended to more than two sampling events, as shown in Figure 1. Here we assume samples are taken from successive generations, giving a sequence of observations $x_0,x_1,\dots , x_t$. Similar to equation 4, the likelihood function is the joint density of the observations:

$$L\left(N_{\text{e}}\right)=f(x_t,x_{t-1}, \dots , x_1,x_0|N_{\text{e}}).$$ (13)

If we let $\underset{¯}{X_i}=(x_0,x_1,\dots , x_i)$ be all the observations up to time i,

$$L\left(N_{\text{e}}\right)=f\left(x_t|\underset{¯}{X_{t-1}}\right)f\left(x_{t-1}|\underset{¯}{X_{t-2}}\right)\dots f\left(x_1|\underset{¯}{X_0}\right)f\left(x_0\right).$$ (14)

We prefer Equation 14 because it illustrates the time dependency among the observations. Again $f\left(x_0\right)$ contains no information about $N_{\text{e}}$ and can be neglected. By using the same argument as in the two-sample case, each $f\left(x_i|\underset{¯}{X_{i-1}}\right)$ is a beta-binomial distribution. The parameters within each beta-binomial distribution are functions of δ and the preceding observations. The remaining question becomes how the parameters in each beta-binomial distribution are obtained. The calculation of the parameters can be generalized by the following four recurring equations,

$$\begin{array}{l}{{\alpha }^{\prime }}_{\left(i\right)}^{}=\frac{\delta {\alpha }_{\left(i-1\right)}}{1+{\alpha }_{\left(i-1\right)}+{\beta }_{\left(i-1\right)}+\delta }\\ {{\beta }^{\prime }}_{\left(i\right)}^{}=\frac{\delta {\beta }_{\left(i-1\right)}}{1+{\alpha }_{\left(i-1\right)}+{\beta }_{\left(i-1\right)}+\delta }\\ {\alpha }_{\left(i\right)}=x_i+{{\alpha }^{\prime }}_{\left(i\right)}^{}\\ {\beta }_{\left(i\right)}=2n-x_i+{{\beta }^{\prime }}_{\left(i\right)}^{},\end{array}$$ (15)

with initial values

$${\alpha }_{\left(0\right)}=x_0+1$$

$${\beta }_{\left(0\right)}=2n-x_0+1,$$

with i runs from $1, \dots , t$. As a result, each of the $x_i$ (given all previous observations) follows a beta-binomial distribution, with parameters

$$f(x_i|\underset{¯}{X_{i-1}})\sim \text{beta-binomial(}2n,{a^{\prime }}_{\left(i\right)}^{},{{\beta }^{\prime }}_{\left(i\right)}^{}).$$ (16)

Moreover, the underlying allele frequency $p_i$ given all observations up to i follows a beta distribution:

$$f\left(p_i|\underset{¯}{X_i}\right)\sim \text{beta}({\alpha }_{\left(i\right)},{\beta }_{\left(i\right)}).$$ (17)

Since the sample sizes and time steps are known, the only parameter remaining in the system is $N_{\text{e}}$, the effective population size. The whole likelihood function is the product of multiple beta-binomial distributions. Therefore the MLE can be obtained by choosing a value of $N_{\text{e}}=\widehat{N_{\text{B}}}$ that maximizes the likelihood function.

Computer Simulations

The first objective of the simulation study was to compare the performance of the proposed $\widehat{N_{\text{B}}}$ estimator with those of the existing methods. The MLNE routine (Wang and Whitlock 2003) and the $F_c$ statistic (Nei and Tajima 1981; Waples 1989) were used as benchmarks. In each iteration, we first simulated the allele frequencies with known $N_{\text{e}}$ across t generations according to the Wright–Fisher model. Multiple independent biallelic loci were run at a time, and samples were then taken with replacement with a sample size of n diploid individuals (a total of $2n$ alleles), as described in Equation 2. Initial allele frequencies were drawn from the uniform distribution. The three methods were then applied to produce three estimates. For $\widehat{N_{\text{B}}}$, the likelihood function was formed using either Equation 5 or Equation 14, depending on the number of sampling events, and the likelihood function was maximized numerically. The lower and upper bounds for searching for the maxima were taken to be 50 and ${10}^7$, respectively. For MLNE the upper bounds for $N_{\text{e}}$ were restricted to 38,000 because of computing limitations. $F_c$ estimates were calculated within the MLNE package. The asymptotic 95% confidence intervals (C.I.) for MLNE and $\widehat{N_{\text{B}}}$ were also calculated by finding the range of $N_{\text{e}}$ in which the log-likelihood dropped by 2 units from its maximum value. Simulations were repeated 1000 times for each parameter setting. Simulations were run in R (R Core Team 2013).

Summary statistics for the three estimators are shown in Table 1. $N_{\text{e}}$ was chosen to be 1000 or 5000. Sample sizes (per generation) were fixed to be 10% of the true population size. Table 1 shows that all three methods slightly overestimated the underlying $N_{\text{e}}$, while $\widehat{N_{\text{B}}}$ had the smallest bias in all cases investigated. In the two-sample scenario there was little difference among the three methods; however, $\widehat{N_{\text{B}}}$ consistently had the smallest variance and bias. For three samples, the differences of the three methods became more pronounced so that the likelihood methods (MLNE and $\widehat{N_{\text{B}}}$) outperformed their moment-based counterpart in terms of having smaller standard deviation and bias. The standard deviation of $F_c$-based estimates was often twice that of the likelihood estimates. This result is consistent with the idea that the likelihood methods are better able to combine data from more than two samples. Within the likelihood family, the mean width of the 95% C.I. was also calculated. The C.I. using $\widehat{N_{\text{B}}}$ is slightly narrower than MLNE given the same significance level, with similar coverage. In short, all the examined scenarios suggested that $\widehat{N_{\text{B}}}$ was superior to the MLNE and $F_c$ estimators.

Table 1. Simulation results.

True $N_{\text{e}}$	n	Method	Mean (SD)	2.5%	97.5%	Mean C.I. width	Coverage
Two samples (sample at t = 0, 8)
1000	100	$F_c$	1,059.7 (253.5)	699.8	1,657.8	—	—
		MLNE	1,080.7 (260.7)	711.3	1,695.4	1,283.3	960
		$\widehat{N_{\text{B}}}$	1,033.2 (247.3)	684.1	1,604.8	1,195.5	956
5000	500	$F_c$	5,272.4 (1,164.5)	3,534.1	8,056.8	—	—
		MLNE	5,276.7 (1,166.7)	3,539.9	8,083.9	6,046.3	970
		$\widehat{N_{\text{B}}}$	5,217.1 (1,149.6)	3,501.6	7,958.1	5,957.4	967
Three samples (sample at t = 0, 4, 8)
1000	100	$F_c$	1,107.8 (638.8)	661.8	2,050.7	—	—
		MLNE	1,076.6 (243.9)	734.9	1,704.6	1,134.2	957
		$\widehat{N_{\text{B}}}$	1,030.9 (226.8)	709.4	1,605.4	1,054.0	960
5000	500	$F_c$	5,567.7 (2,038.2)	3,165.9	10708.0	—	—
		MLNE	5,254.0 (1,153.4)	3,530.2	8,198.1	5,427.4	950
		$\widehat{N_{\text{B}}}$	5,202.0 (1,138.5)	3,495.9	8,008.4	5,352.2	953

For each parameter setting, 1000 replicate populations were simulated and all three methods are used to estimate $N_{\text{e}}$. The true $N_{\text{e}}$, sample size per generation, and number of temporal samples are shown. A total of 500 unlinked loci are used in each run and the initial allele frequencies are sampled from the uniform distribution. The mean, standard deviation, 2.5 and 97.5 percentiles of the 1000 runs are reported. For MLNE and $\widehat{N_{\text{B}}}$, the mean width of the 95% confidence interval (C.I.) is also computed. The last column shows the number of C.I.’s (of 1000 simulations) that cover the true value $N_{\text{e}}$.

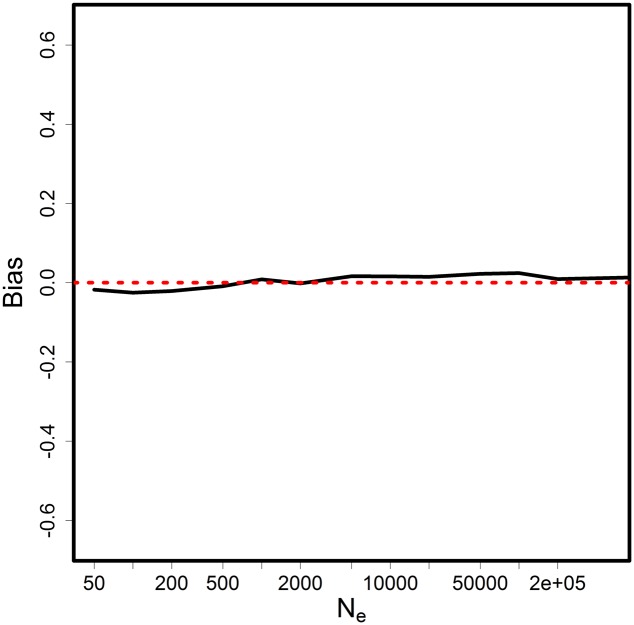
A second set of simulations examined the bias and consistency of the new estimator for a range of $N_{\text{e}}$ values. As the central assumption of the method is that $N_{\text{e}}$ is sufficiently large for a continuous approximation to be valid, it is interesting to investigate the performance of the $\widehat{N_{\text{B}}}$ estimator over a wide range of $N_{\text{e}}$, including small values. A plot of the bias against true $N_{\text{e}}$ is found in Figure 2. For the smaller values of $N_{\text{e}}$, $\widehat{N_{\text{B}}}$ slightly underestimated the population size by <2%, while for $N_{\text{e}}=500$ and onward $\widehat{N_{\text{B}}}$ was slightly biased upward by no more than 2%. This graph supports that $\widehat{N_{\text{B}}}$ is unbiased throughout a wide range of true $N_{\text{e}}$ from 50. Thus, the new estimator provides an inferential statistic that is not available through prior methods.

Figure 2.

Plot of bias of the $\widehat{N_{\text{B}}}$ estimator against true $N_{\text{e}}$. The bias (solid line) is quantified as the percentage difference relative to the true $N_{\text{e}}$. Sample size was 10% of the true $N_{\text{e}}$ with 1000 loci. Two samples were taken 10 generations apart. The bias approaches 0 (red dotted line) if the estimator is unbiased.

Nonconstant $N_{\text{e}}$ and Likelihood-Ratio Tests

Given three or more samples over time, we can consider the possibility that $N_{\text{e}}$ is different in each sampling interval. This can be done through modifying Equation 15 to allow nonconstant δ. It is also possible to use the same approach to fit a dynamic model to the data. For example, Wang (2001) demonstrated fitting an exponential growth model with two parameters: initial $N_{\text{e}}$ and growth rate. In general, a likelihood-ratio test (LRT) can be constructed to compare models and hypotheses. The test statistic is twice the difference in the log-likelihood values under the null and alternative hypotheses and is asymptotically chi-square distributed with degrees of freedom equal to the difference in the number of parameters between the two models. The following simulated example illustrates how a LRT is constructed.

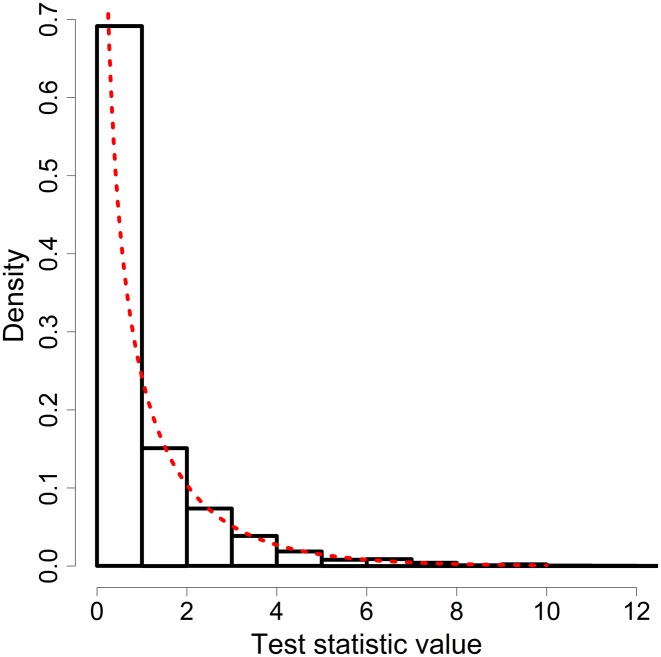
Consider a three-sample case with samples taken at $t=0,4$, and 8, in which we wish to test whether $N_{\text{e}}$ is constant throughout the sampling period. This can be done by setting up the following hypotheses: H₀: $N_{\text{e}}$ is constant vs. H₁: there are two distinct $N_{\text{e}}$’s for the period between $t=0$ and $t=4$ and between $t=4$ and $t=8.$ We can fit two models representing the two hypotheses to the data, one with a single $N_{\text{e}}$ and the other with two different $N_{\text{e}}$’s. Under the null hypothesis (i.e., given H₀ is true), the test statistic asymptotically follows a chi-square distribution with 1 d.f. This can be verified by simulating 5000 replicates as shown in Figure 3.

Figure 3.

Histogram of the likelihood-ratio test statistic under H₀ for 5000 simulations. Three temporal samples were drawn in each replicate. The red line represents the theoretical density of a chi-square distribution with 1 d.f.

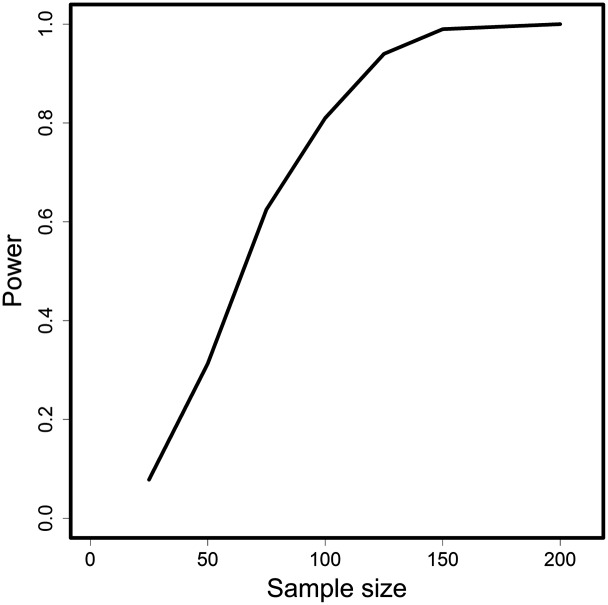
The statistical power of the test can be exemplified by setting up a specific alternative hypothesis. For example, if the underlying population drops from 10,000 in $t=0, 4$ to 1000 in $t=4,8$, then the power of the test is the probability of rejecting the null hypothesis. There are several parameters controlling the power, one of which is the sample size, n (Figure 4). In the particular example shown, a sample size of $n=100$ is required to attain a power of 80%.

Figure 4.

Statistical power against sample size. A specific H₁ was chosen as described in the text, with 1000 independent loci.

Computational Effort

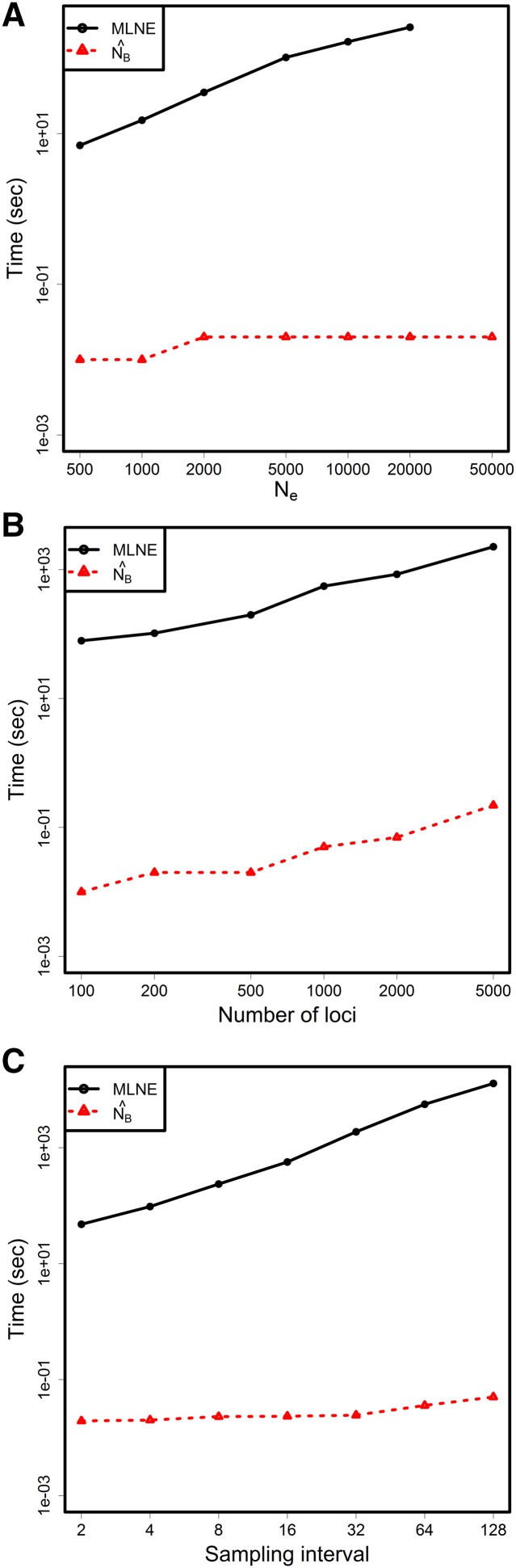
With the use of the beta and binomial distributions in modeling genetic drift and sampling events, closed-form solutions for the integrals in Equations 11 and 12 are obtained. As a result, the likelihood function (Equation 14) is much simplified and no longer involves summations over all the nuisance parameters as in the full-likelihood model (Equation 1). The comparison of the computation time between MLNE and $\widehat{N_{\text{B}}}$ is shown in Figure 5. For the MLNE package, increases in $N_{\text{e}}$ lead to increases in the number of elements in the transition matrix and therefore in the computing time (Williamson and Slatkin 1999; Wang 2001). For $\widehat{N_{\text{B}}}$, continuous approximation is used and the structure of the transition probabilities is approximately the same for all $N_{\text{e}}$. Hence the computing time remains low for any $N_{\text{e}}$. For both MLNE and $\widehat{N_{\text{B}}}$, computing time increases with the number of loci used in a similar fashion, but $\widehat{N_{\text{B}}}$ remains several thousand times faster than MLNE. The speed advantage of $\widehat{N_{\text{B}}}$ also becomes more distinct with increasing sampling interval, because $\widehat{N_{\text{B}}}$ does not require calculation of the power of the transition matrix. It should be noted that the two methods are not coded in the same programming language (Fortran for MLNE and R for $\widehat{N_{\text{B}}}$), so these results should not be considered a direct comparison of the two algorithms. However, it likely underestimates the speed advantage of $\widehat{N_{\text{B}}}$ over MLNE because R is a script language, which is typically slower than a compiled language like Fortran. Nevertheless, the new method speeds up estimation by a factor of 1000–10,000 for large $N_{\text{e}}$ without sacrificing accuracy.

Figure 5.

Comparison of computational effort (in seconds) between MLNE and $\widehat{N_{\text{B}}}$. A shows the computational time against true $N_{\text{e}}$. $N_{\text{e}}$ of 50,000 was not run for MLNE because this exceeds the limits of the software. B shows the computational time against the number of loci used in each iteration. C plots the computing time against sampling interval.

Real Example

A real data set from Cuveliers et al. (2011) was used to demonstrate the use of $\widehat{N_{\text{B}}}$. Six temporal samples spanning >10 generations were collected between 1957 and 2007 to infer the effective population size of North Sea sole. The sample sizes were ∼135–220 individuals per generation with 11 microsatellite markers being genotyped. The number of alleles in these loci ranges from 13 to 39. We used $\widehat{N_{\text{B}}}$ to estimate the overall N_e throughout the entire sampling horizon. The effective population size during the period was estimated to be 2512 with finite 95% confidence limits of 1661 and 4365. The published estimate using MLNE (Wang 2001) was 2169 (C.I. = 1221–5744), while the estimate from the F-statistic (Waples 1989) was 2247 (C.I. = 1127–8370). The complete result can be found in table 2 of Cuveliers et al. (2011, p. 3561). We found that all three estimates mostly overlap with each other, indicating the consistency among the temporal estimators. The estimate from $\widehat{N_{\text{B}}}$ is slightly larger than those obtained by MLNE and F-statistics, but it is the most precise one with the narrowest confidence interval. $\widehat{N_{\text{B}}}$ also showed a significant reduction in computing time; it is ∼600 times faster than MLNE in this particular example.

Discussion

The model

In theory, the full-likelihood model (Williamson and Slatkin 1999) for estimating $N_{\text{e}}$ from temporal samples should be the most accurate but is not practical because of computational limitations. MLNE, as a derivation of the full-likelihood model, intentionally omits some of the smaller transition probabilities to enhance computational feasibility. The $\widehat{N_{\text{B}}}$ estimator is also an approximation to the full likelihood, but makes use of the continuous approximation to simplify the calculations. Previous studies by Williamson and Slatkin (1999) and Wang (2001) showed that the maximum-likelihood methods are more accurate and precise than the F-statistics, and this article further confirms that $\widehat{N_{\text{B}}}$ is no exception. The comparison between MLNE and $\widehat{N_{\text{B}}}$ showed that $\widehat{N_{\text{B}}}$ is a better alternative to MLNE in a moderately large $N_{\text{e}}$ scenario. In our examined cases $\widehat{N_{\text{B}}}$ produces a smaller variance and narrower confidence interval than MLNE, yielding a more precise estimate of $N_{\text{e}}$. The bias of $\widehat{N_{\text{B}}}$ is also negligible, indicating that the approximations hold over a wide range of true $N_{\text{e}}$.

Perhaps the most important feature of $\widehat{N_{\text{B}}}$ is in relaxing the $N_{\text{e}}$ upper bound. Since the dimension of the Wright–Fisher transition matrix is determined by $N_{\text{e}}$, MLNE stops the calculation when $N_{\text{e}}$ exceeds a certain value. The current threshold on my workstation is ∼38,000 while the user manual from MLNE suggests 50,000. This upper bound also applies to the calculation of the upper confidence interval, making the practical range of true $N_{\text{e}}$ even smaller. $\widehat{N_{\text{B}}}$ relaxes this bound to over several million without causing computational issues. As a result, precise estimation of contemporary $N_{\text{e}}$ can be applied to more species. Another distinct advantage is the computing speed, which is increased by a factor of ≥1000 in most scenarios. Most calculations in $\widehat{N_{\text{B}}}$ are done within seconds. Field biologists may not appreciate this improvement as most of their time is spent on data collection; however, with the anticipated advance in DNA sequencing technology, large amounts of loci can be sequenced at a time with low cost. The ability of existing software to handle such a data set is questionable. Furthermore, with the increasing popularity of the use of computer simulation in population genetics (such as ms by Hudson 2002), in which the computing time is multiplied by the number of repeated simulations, $\widehat{N_{\text{B}}}$ provides an efficient algorithm to help scientists evaluate their simulations rapidly and accurately.

Usage

As discussed above, $\widehat{N_{\text{B}}}$ is designed for moderately large $N_{\text{e}}$ populations and this explains why our simulations focused in these scenarios. Although we showed that $\widehat{N_{\text{B}}}$ is unbiased even for small values of $N_{\text{e}}$, we suggest using the full-likelihood method for the extremely small $N_{\text{e}}$ problem (when $N_{\text{e}}$ < 100). In determining sample size, it has to be viewed relative to the true $N_{\text{e}}$ of the population. It is shown in our simulations that sampling 10% of the individuals is able to estimate $N_{\text{e}}$ accurately, with the use of ∼500 independent loci. Interested readers can refer to Waples (1989) and Wang (2001) for more details about the effect of sampling effort on temporal methods.

Excluding rare alleles is not unusual in population genetics studies. For instance, LDNE (Waples and Do 2008) imposes several cutoffs for rare alleles. Wang (2001) showed that the moment-based F-statistics induces bias with rare alleles, while the likelihood methods are less sensitive to small allele frequency as they make use of the full distributional information of the Wright–Fisher model. We analyzed empirically the goodness of fit of the beta distribution in modeling allele frequency in the Appendix. We showed that the approximation is indistinguishable from the true continuous model when frequent alleles are used, and it still holds when the observed allele frequency is down to ∼0.05. As a result we suggest that in most cases it is safe to include alleles with observed allele frequency >5%.

In the review by Luikart et al. (2010) they emphasized the desirability of developing new methods that are able to distinguish between moderate and large $N_{\text{e}}$ and that future development of $N_{\text{e}}$ estimators should allow for the possibility of genotyping many loci. The methods developed here allow for expansion in these two directions, both for estimating effective population sizes and for testing for significant differences (or trends) in population sizes from temporally spaced samples.

R package

An R package “NB” has been created to implement $\widehat{N_{\text{B}}}$ as described in this article. The package allows more flexibility, including unevenly temporal-spaced samples and nonconstant sample size. As demonstrated in our worked example, multiallelic loci are accepted in the R package through the use of Dirichlet-multinomial distribution. It also contains a sample data set and a help document to describe the usage of the package. It is available for download at http://cran.r-project.org/web/packages/NB/.

Appendix

Since the approximation stated in Equation 8 is one of the several key ideas in this article to speed up the current estimation of $N_{\text{e}}$, it is essential to evaluate how good the approximation is. Equation 8 in the main text is

$$\begin{array}{l}{\displaystyle {\int }_0^{1}f\left(p_t|p_0,N_{\text{e}}\right)f\left(p_0|x_0\right)d{p}_0}\\ \approx \text{beta}\left({\alpha }^{\prime }=\frac{\delta \left(x_0+1\right)}{2n+2+\delta },{\beta }^{\prime }=\frac{\delta \left(2n-x_0+1\right)}{2n+2+\delta }\right).\end{array}$$

The left-hand side of Equation 8 is considered as a hierarchical relationship, that $p_t$ is distributed as beta given a value of $p_0$, while $p_0$ itself is also distributed as beta conditioning on the initial observed count $x_0$ (which is a fixed value). Two sources of randomness are involved and the integral sums over all possible values of the intermediate $p_0$. However, this kind of integration seldom has an analytical solution. In this article we suggest that this integral can be well approximated by another beta distribution, as suggested in Equation 8.

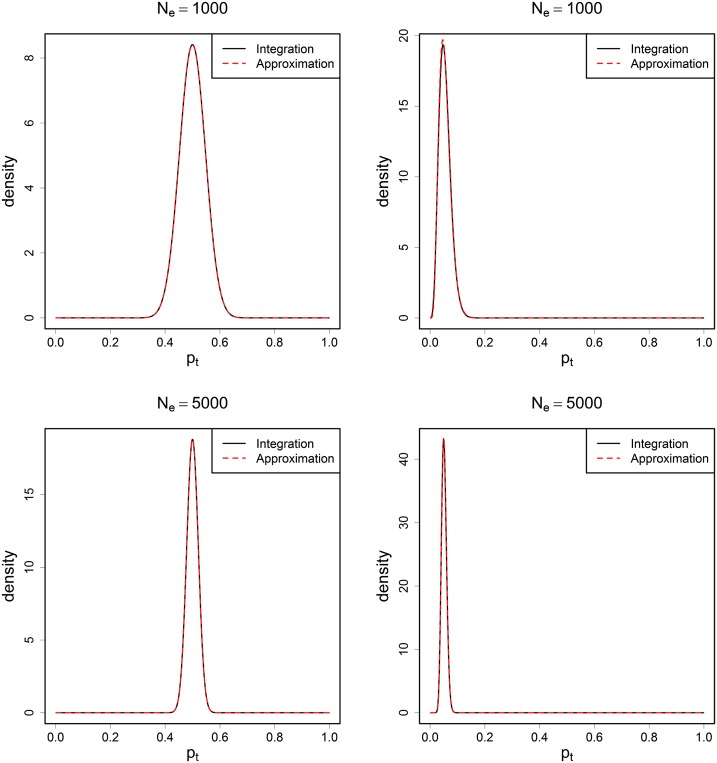
We examined how close the approximation is to the actual integral. Two values of $N_{\text{e}}$ were studied: 1000 and 5000, with eight generations between the two samples taken. Sample size was set to 10% of the true $N_{\text{e}}$. Under these settings, both low allele frequency (0.1) and even allele frequency (0.5) scenarios were tested. Plots of the results can be found in Figure A1.

Figure A1.

The plots of the conditional density $p_t|x_0$, where $N_{\text{e}}$ was set to be 1000 (top row) and 5000 (bottom row). Sample size was 10% of the true $N_{\text{e}}$ per generation. Two samples were drawn with a sampling interval of eight generations. The left column represents the cases when frequent alleles were used (allele frequency ∼0.5), and the right column represents the cases when rare alleles were used (allele frequency ∼0.05). The conditional densities were calculated from two methods: numerical integration (black solid line) and by approximation (red dashed line).

From the plots we can see that the two lines representing the two methods overlap with each other and are visually indistinguishable. This indicates that in moderately large $N_{\text{e}}$ the use of a beta distribution is a good approximation to the integral. Furthermore, the approximation holds for a wide range of allele frequencies, including the cases where rare alleles are used.