CONSTRUCTING MULTI-RESOLUTION MARKOV STATE MODELS (MSMS) TO ELUCIDATE RNA HAIRPIN FOLDING MECHANISMS

Abstract

Simulating biologically relevant timescales at atomic resolution is a challenging task since typical atomistic simulations are at least two orders of magnitude shorter. Markov State Models (MSMs) provide one means of overcoming this gap without sacrificing atomic resolution by extracting long time dynamics from short simulations. MSMs coarse grain space by dividing conformational space into long-lived, or metastable, states. This is equivalent to coarse graining time by integrating out fast motions within metastable states. By varying the degree of coarse graining one can vary the resolution of an MSM; therefore, MSMs are inherently multi-resolution. Here we introduce a new algorithm Super-level-set Hierarchical Clustering (SHC), to our knowledge, the first algorithm focused on constructing MSMs at multiple resolutions. The key insight of this algorithm is to generate a set of super levels covering different density regions of phase space, then cluster each super level separately, and finally recombine this information into a single MSM. SHC is able to produce MSMs at different resolutions using different super density level sets. To demonstrate the power of this algorithm we apply it to a small RNA hairpin, generating MSMs at four different resolutions. We validate these MSMs by showing that they are able to reproduce the original simulation data. Furthermore, long time folding dynamics are extracted from these models. The results show that there are no metastable on-pathway intermediate states. Instead, the folded state serves as a hub directly connected to multiple unfolded/misfolded states which are separated from each other by large free energy barriers.

1. Introduction

Conformational changes are crucial for a wide range of biological processes including protein folding[1], RNA folding[2] and the operation of key cellular machinery[3-5]. Extensive genetic, biochemical, biophysical and structural experiments can be performed to understand these conformational changes[3-5]. However, probing the mechanisms of conformational changes at atomic resolution is very difficult experimentally and without these details it is impossible to understand the fundamental chemistry they perform. Computer simulations may complement such experiments by providing dynamic information at an atomic level. However, there is a gap between the timescales where interesting biologically relevant conformational changes occur (typically microseconds and up) and those we can simulate at atomic resolution (typically only tens of nanoseconds). The length of atomistic simulations is limited by the need to take small timesteps (1 or 2 fs), which is determined by high frequency motions such as chemical bond stretching. One natural way to bridge this timescale gap is to use coarse grained models where the smallest unit of the system represents a group of atoms[6, 7]. In these models, much longer timesteps are allowed since the high frequency motions are not explicitly simulated. Coarse grained simulations work well for a variety of problems[8-12]; however, these models sacrifice accuracy for speed, making them less than ideal for investigating the detailed mechanisms of conformational changes.

An alternative approach to overcome the timescale gap is to build discrete-time Markov State Models (MSMs) [13-17]. These models may be built from many short (nanosecond timescale) simulations and then propagated to give long timescale dynamics, such as processes occurring on microsecond timescales or even longer. MSMs partition phase space into a number of distinct states, called metastable states, such that intra-state transitions are fast but inter-state transitions are slow. Such separation of timescales ensures that the model is Markovian, in that the probability of being in a given state at time t+Δt depends only on the state at time t. In an MSM, the time evolution of a vector representing the population of each state may be calculated by repeatedly left-multiplying by the transition probability matrix.

$$P\left(n\Delta t\right)={\left[T\right(\Delta t\left)\right]}^{n}P\left(0\right)$$ (1)

where P(nΔt) is a vector of state populations at time nΔt and T is the column-stochastic transition probability matrix. Any model is Markovian for a sufficiently long lag time (τ = Δt), because the system is able to relax to an equilibrium distribution from any arbitrary starting distribution after one lag time. The key point is to build a model with a lag time that is shorter than the timescale of the process of interest with a reasonable number of states. This requires a very good state decomposition, which is difficult. A few different approaches have been developed to address this issue[13-18]. There also exist other methods to bridge the timescale gap such as milestoning [19]. However, most of these methods require the reaction coordinate is known a priori, while this information is often difficult to obtain.

MSMs are also multi-resolution in nature[13, 14]. In order to achieve a Markovian model at a certain lag time, the states must be defined such that large internal free energy barriers are avoided and conformations within the same metastable state can interconvert within one lag time. Thus, the number of states needed in an MSM depends on the desired lag time. The smaller the lag time is, the more states the MSM needs to ensure that dynamics within each state are memory-less after one lag time. A short lag time would result in a high resolution MSM having many metastable states, capturing numerous free energy minima separated by small barriers. A longer lag time results in a low resolution MSM with only a few states, each of which contains multiple local free energy minima. We introduce a new algorithm, Super-density-level Hierarchical Clustering (SHC), to construct MSMs at different resolutions for conformational dynamics. To our knowledge, SHC is the first algorithm focusing on generating MSMs at multiple resolutions.

The key insight of the SHC algorithm is to cluster conformations hierarchically using super density level sets in a bottom-up fashion starting with the densest regions of phase space, which correspond to the bottoms of free energy minima. This algorithm can generate multi-resolution models by tuning the super density level sets, and each level of resolution constitutes a discrete-state MSM with a particular partitioning of phase space. At low resolution, it generates a coarse state decomposition with a small number of metastable states while at high resolution it generates a finer state decomposition with more metastable states. This leaves one the flexibility to select an MSM at the best resolution to study their biological problem.

The procedure to build MSMs using SHC is as follows. (1) Partition the conformations into a large number of states, called microstates, according to their structural similarity. An approximate K-centers clustering algorithm[20] is used here as it gives states with approximately uniform size, resulting in a correlation between the population of each state and its density. (2) Split the microstates into n density levels ordered from high to low density (L= {L₁, … L_n}) such that each level contains approximately the same number of conformations. Then construct super density level sets S_i, where S_i = L₁ ⋃ L₂…⋃ L_i−1 ⋃ L_i. Thus each super density level contains all previous levels S₁ ⊆ S₂… ⊆ S_i. (3) Within each super density level (S_i), perform spectral clustering to group kinetically related microstates. Metastable regions are better separated at high density super levels, since most of the fuzzy microstates in the transition region are excluded at these levels. Now, build a graph representing the connectivity of the states across super density levels. Then generate gradient flows along the edges of the graph from low to high density levels. Each attraction node (or attractive basin) where the gradient flow ends is assigned to a new metastable state. (4) Assign every microstate not belonging to an attraction node to the metastable state it has the largest transition probability to. Thus we have a complete state decomposition for an MSM. Furthermore, this procedure may be repeated with different super density level sets to construct MSMs at different resolutions. The larger the number of super density levels, the finer the resolution and the larger the number of metastable states in the final MSM.

In order to test SHC, we apply it to a small RNA hairpin with microsecond time scale dynamics: an eight nucleotide RNA GCAA tetraloop with the sequence 5′-GCGGCAGC-3′. It has 4 bases in the loop and two stem base pairs as shown in Figure 1. RNA hairpins are a ubiquitous secondary structure motif often involved in tertiary contacts[21]. Much experimental work has been done on these systems as a step towards understanding larger RNA molecules but knowledge of their folding is still incomplete[22-28]. Despite their small size, even eight nucleotide hairpins fold on a microsecond timescale[23], about two orders of magnitude longer than typical atomic simulations. However, using SHC, we are able to construct multi-resolution MSMs from many short 45 ns atomistic simulations. These models are able to predict microsecond timescale dynamics. We compare MSMs at different resolutions and also validate them by confirming their ability to reproduce the original simulation trajectories. Furthermore, we extract the kinetics between the most populated metastable states from our MSMs. The results suggest that the folded state is a hub connected to many non-native metastable states that are mostly uncoupled from one another. No metastable intermediate states are identified, while there are a few misfolded states such as states with shifted base pairing or an unfolded loop. This indicates that folding of an eight nucleotide RNA hairpin with only two stem base pairs might be different from RNA hairpins with longer stems where stable thermodynamic intermediate states were seen in previous simulations[22].

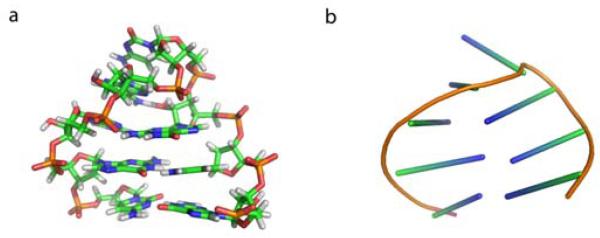
Figure 1.

(A) Structure of the 8 nucleotide RNA GCAA tetraloop, generated by truncating the two terminal base pairs from the NMR structure of a 12 nucleotide tetraloop (PDB ID 1zih). (B) The cartoon representation of the same structure using sticks to represent the orientation of the bases. The same cartoon representation will be used in Figure 6 to illustrate representative structures from different metastable states.

2. Methods

Here we explain the SHC algorithm in detail using an RNA GCAA tetraloop as an example. The dataset we examine here contains 9,963 45ns explicit solvent molecular dynamics simulations with an aggregate simulation time of 448 microseconds. Conformations are saved every 0.2 ns, and the total number of conformations is about 2.3 million. These simulations are initiated from different metastable regions of phase space identified by short Simulated Tempering[29, 30] simulations following the Adaptive Seeding Method (ASM)[31]. More simulation details are available in Appendix A.

2.1. Partitioning conformations into microstates

Modern computer simulations can easily generate massive data sets with millions of conformations, making analysis of these data sets computationally challenging. To reduce the dimensionality of the data, we first group conformations into a large number (a few thousand or tens of thousands) of small clusters called microstates based on their structural similarity, in this case measured using the Root Mean Square Deviation (RMSD) between all heavy atoms. Each microstate must be small enough to ensure conformations in the same state can interconvert rapidly. An approximate K-centers clustering algorithm[20] was used here to generate microstates by minimizing the maximum cluster radius, where the cluster radius is defined as the maximum heavy atom RMSD distance between the cluster center and any other conformation within the cluster. The detailed implementation of the algorithm is discussed elsewhere[18, 20], and the code for the approximate K-centers clustering is available through the MSMBuilder package[18]. This algorithm has a computational complexity of O(kN), where k is the number of clusters and N is the number of conformations to be clustered. Moreover, it gives states with approximately equal radii. As a result, there is a correlation between the population of each microstate and its density, allowing us to define density levels in the subsequent steps.

We have clustered ~2.3 million conformations into 10,000 microstates, and the same microstate decomposition is used to build all MSMs in this work. The cluster radius distribution has a sharp peak around 4 Å, confirming that the clusters have approximately equal radius (data not shown). Thus, the population of each microstate is a reasonable indicator of its conformational density. However, we note that even small differences in the radius of microstates may imply relatively large variations in their volumes due to the high dimensionality of conformation space. We empirically find that assuming all clusters have approximately equal volumes is useful. In the future, we can improve the density estimation step by working on low dimensional sub-manifolds where density estimation is consistent and accurate. These low dimensional sub-manifolds can be constructed with nonlinear dimensionality reduction techniques[32].

2.2. Super density level set formation

In this step, we first split the microstates into n density levels L= {L₁, … L_n}. As discussed above, the density of microstates d₁…d_k can be estimated from their populations by dividing number of conformations within each microstate by the total number of conformaitons. We order microstates according to the value of d_i and classify the microstates into n consecutive levels. Each level contains about the same number of conformations. Density levels are ordered from high to low density, and labeled 1 to n. For example, from our RNA dataset, we have generated a density level set with three levels L= {L₁, L₂, L₃}. L₁, L₂, and L₃ contain 146, 615, and 1810 microstates respectively, and approximately an equal number of conformations (each level contains about 25% of the total conformations, the remaining conformations are ignored until the final step of the algorithm). Thus, level L₁ has the least number of microstates and contains only the highest density regions. From the density level set, we can easily construct the super density level set S= {S₁, …, Sn} by defining S_i = L₁ ⋃ L₂…⋃ L_i−1 ⋃ L_i. Each super density level contains all previous levels S₁ ⊆ S₂… ⊆ S_i. In our example, three super density levels S₁, S₂, and S₃ are created, containing 25%, 50% and 75% of the total conformations respectively. Recently, a topological data analysis approach[33, 34] based on similar ideas regarding clustering in density level sets has been successfully applied to perform geometric clustering on biomolecular data. However, we found in this study that super level sets yield better results than density level sets in identifying kinetically metastable states (data not shown).

2.3. Spectral Clustering within super density levels

Spectral clustering [35-38] is performed on a transition probability matrix within each super density level (S_i). Since these transition probablity matrixs are generated by normalizing number of transitions between pairs of micorstates by counting directly from the original simulation trajectories, applying spectral clustering on them is able to lump kinetically related microstates into larger metastable states. Metastable regions are better separated in high density super levels, since most of the fuzzy microstates in transition regions are excluded at these levels. For example, in the RNA dataset, multiple disconnected blocks are found in the transition probability matrix for level S₁, indicating good separation of metastable regions. When we move up to levels containing more low density microstates, less and less disconnected blocks are found in the transition probability matrix, and eventually the matrix becomes completely connected. In the example with three density levels, the first level S₁ contains 35 metastable states, S₂ contains 25, and S₃ contains only 6 states. In order to identify nearly disconnected blocks in a transition matrix, we choose eigenvalues very close to 1 for spectral clustering. In particular, a constant spectral gap of Δλ = 0.0001 is used for this example.

Next we build a graph representing the connectivity of the metastable states across super density levels. Figure 2 is an example of such a graph with three levels. Each node in the graph represents one metastable state. As discussed above, the number of nodes in each level decreases from S₁ to S₃. In S₁, there is a large node (node 1) containing 64% of all the conformations in that level. Similar nodes can also be found in other levels such as node 2 (83%) in S₂ and node 3 (99%) in S₃. These results suggest that there is a large metastable state corresponding to the folded state, to be discussed in more detail in the Results and Discussion section. In the next step, gradient flows are generated along the edge of the graph from low to high density levels. Nodes that do not have any flow into denser states correspond to basins of attraction, or metastable states. For example, node 1 is an attraction node, while nodes 2 and 3 are not. As shown in Figure 2, there are 46 attraction nodes in this model (35 in S₁ and 11 in S₂). Thus the model contains 46 metastable states.

Figure 2.

A graph describing the connectivity of the metastable states generated by SHC. Each node in the graph denotes a single metastable state. Each row corresponds to one super density level: states belonging to S₁ (in red), S₂ (in blue), and S₃ (in green) contain 25%, 50%, and 75% of all the conformations respectively. Two nodes are connected if they share microstates, and the arrows represent the gradient flows from low density to high density regions, i.e. from S₃ to S₁. Arrows representing self transitions are plotted at attraction nodes where the flow ends. The radius of each node is scaled linearly by its population within each super level.

2.4. Assigning microstates not in attraction nodes

In the previous step, all the attraction nodes were selected as metastable states. Here, we will assign the remaining nodes to metastable states, as well as microstates that were not included in any of the density levels. This is achieved by computing the transition probabilities from each of these microstates to all possible metastable states, and assigning each microstate to the metastable state it has the largest transition probability to. If a particular microstate cannot transition to any of the metastable states in a single step we consider a progressively larger number of steps until we see transitions between this microstate and some metastable state.

Following the above steps yields a complete state decomposition for an MSM. In the example shown in Figure 2, a 46-state MSM is generated. In order to construct MSMs at different resolutions we repeat the same procedure using different numbers of super density levels.

3. Results and Discussion

3.1. Constructing MSMs at different resolutions

Using SHC, we have constructed four different MSMs by varying the number of super density levels (N_L) all with a lag time of 0.2 ns. The super density level set is defined as S= {d₀/N_L, 2d₀/N_L,…, d₀}, where d₀ = 0.75. Specifically, we used 3, 6, 9, and 15 super density levels, yielding MSMs referred to as L3 MSM, L5 MSM, L9 MSM and L15 MSM respectively. In addition, we also built a model (L1 MSM) with L = 1 as a control. Some properties of these models are listed in Table 1.

Table 1.

Number of states (N), metastability (Q), and average self transition Probability (<T_ii>=Q/N) for five MSMs generated by SHC using super density level sets containing L levels.

L	1	3	6	9	15
N	6	46	57	63	68
Q	5.95	44.3	54.2	59.3	63.4
<Tii>	99.1%	96.3%	95.1%	94.1%	93.2%

The first property in the table is the number of macrostates in each MSM. This number increases with L, and L15 MSM contains more than ten times more states than L1 MSM. With many more states, L15 MSM is a higher resolution model than L1 MSM. Thus SHC is able to generate multi-resolution MSMs by changing the number of super density levels N_L. Metastability is another important property for an MSM. A good MSM should contain a state decomposition which maximizes the separation of timescales. The self-transition probability, indicating the stability of each macrostate, is a simple and straightforward way to check if there is a good separation of timescales. The metastability (Q) listed in Table 1 is defined as the sum of the self-transition probabilities (T_ii) of each macrostate. Table 1 also shows the average self transition probability: <T_ii> = Q/N, where N is the number of metastable states. <T_ii> decreases with L, indicating higher resolution models have smaller average self transition probabilities. This is consistent with the fact that higher resolution models will capture smaller free energy minima, which are separated by smaller free energy barriers and therefore less metastable.

Another interesting property, which is not listed in the table, is the population of each macrostate. For the control model L1 MSM, the populations of the six states ordered from high to low are: 98.0%, 1.6%, 0.2%, 0.05%, 0.05%, and 0.05%. Only two states have populations greater than 1%, and the rest have negligible populations. A closer look at the data shows that these four states each contain only a single microstate, and they are almost disconnected from the rest of phase space. Thus these four states might not be significant metastable regions, but just noise due to insufficient sampling. This is one issue with spectral clustering algorithms such as PCCA[37] and PCCA+[38], which tend to first separate the most disconnected blocks from the transition probability matrix. This makes it difficult to choose a proper number of metastable states in order to identify all the significant metastable regions. SHC is able to overcome this issue by clustering from the highest density super level, which guarantees that the most populated metastable regions are identified first. L3 MSM, L5 MSM, L9 MSM, and L15 MSM contain 8, 15, 12, and 10 states with populations larger than 1% respectively.

3.2. Validating MSMs

In this section, we will validate the MSMs discussed above in two ways: implied timescales and Chapman-Kolmogorov equation.

Implied timescales

Examining the behaviors of the implied timescales is one way to check if the model is Markovian as first suggested by Swope. et. al.[16]. Implied timescales (τ_k) can be computed from the eigenvalues of the transition matrix T as shown below:

$${\tau }_k=-\frac{\tau }{\ln {\mu }_k\left(\tau \right)}$$ (2)

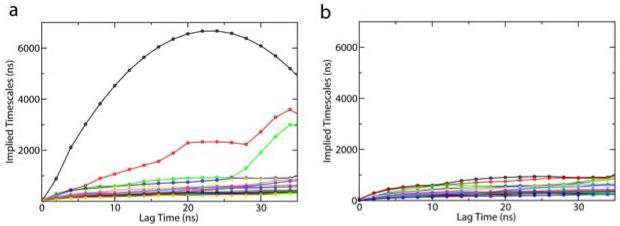
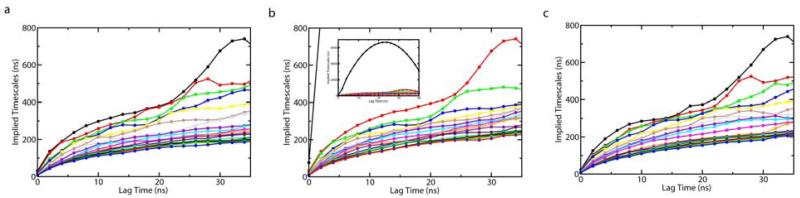
where μ_k is an eigenvalue of the transition matrix with the lag time τ. Each implied timescale describes an aggregate transition between subsets of macrostates. If the model is Markovian and Equation (1) holds, the exponentiation of T should be identical to an MSM constructed with a longer lag time, and the implied timescales will be independent of the lag time. This requires that lag times are sufficiently long. The shortest lag time for this condition to hold is defined as the Markovian time, which is correlated with the longest internal equilibrium time of any state. Figure 3 displays implied timescales plots as a function of the lag time for L3 MSM. As shown in Figure 3 (a), the implied timescales level off around a lag time of 20ns. This implies that the model is Markovian with long enough lag times. However, big fluctuations are observed for the three slowest timescales. A further investigation shows that these slow timescales are due to low-population states which are nearly disconnected from the other states. If we exclude three states (with populations 0.1%, 0.09%, and 0.04%) containing very few non-self transition counts from our analysis, these slowest timescales disappear (see Figure 3 (b)). The implied timescale plots for other resolution MSMs also level off as shown in Figure 4. These results suggest that MSMs generated from SHC are Markovian with sufficiently long lag times. Higher resolution MSMs with a finer discretization of phase space should have shorter Markovian times, since the intra-state equilibrium times are shorter. Looking at Figure 4, the implied timescales of L15 MSM seem to level off slightly faster than those of L6 MSM. However, it is hard to tell by eye whether there is any large difference in the Markovian times for these models. Thus, the implied timescales check has some drawbacks. It is difficult to determine by eye if and where the implied timescales level off. In addition, small uncertainties in the eigenvalues can induce large uncertainties in the implied time scales[14].

Figure 3.

Top twenty implied timescales as a function of the lag time for the L3 MSM (L3 denotes the super density level set containing 3 levels) The plots are generated by using (a). the transition probability matrix with all 46 states. (b) the transition probability matrix with only 43 states with three nearly uncoupled states excluded (These three states have very few transition counts to other states).

Figure 4.

Top twenty implied timescales as a function of the lag time for (a) L6 MSM, (b) L9 MSM, and (c) L15 MSM. L6, L9, and L15 indicate that 6, 9 and 15 super density levels are used to generate these MSMs respectively. The insert in (b) is the same as the main figure except that the y axis goes up to 7 microseconds in order to show one very long implied timescale.

Chapman-Kolmogorov Check

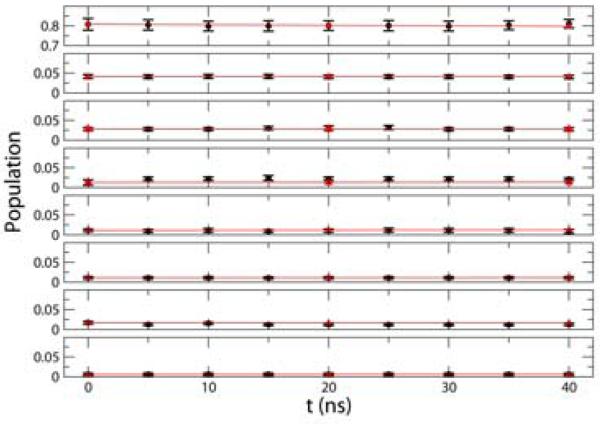
An alternative way to validate MSMs is to directly check if Equation (1), a form of the Chapman-Kolmogorov equation, holds[14]. Figure 5 shows the time evolution of the populations of the top eight most populated states in L3 MSM. Populations extracted from the raw data are compared with those generated by the MSM starting from the same initial populations (see Equation (1)). As shown in Figure 5, these populations agree well within statistical error. Similar agreement was found for the other MSMs as well (data not shown). These results suggest that MSMs generated by SHC are consistent with the original dataset from which they were constructed. The final obervation is that population distriutions are almost flat, which may suggest that the starting conformations of the simulations generated from the Adaptive Seeding Method[31] are already close to the equilibrium distribution (See Appendix 1 for details).

Figure 5.

Comparison between the time evolution of the populations of the eight most populated states (with populations larger than 1%) in the L3 MSM (red) and the raw data (black). The error bars in the black curves are the standard deviations computed from one hundred boot strapping runs each of which randomly selected 8,000 of 9,963 trajectories with replacement. A 20ns lag time is used to build the transition probability matrix based on the L3 MSM state decomposition.

3.3. RNA hairpin folding mechanism

Despite the small size of RNA hairpins, there is some debate over whether they fold in a two-state or multi-state manner. Thermodynamic measurements such as temperature melting[25] support the two-state model, while kinetic experiments such as temperature jump suggest a multi-state model[39]. Using the laser temperature jump technique, the Gruebele group[23] observed two unfolding relaxation phases of the eight nucleotide gcUUCGgc hairpin at low temperatures: a fast phase of 1-2 microseconds, and a slow phase of 5-10 microseconds[23, 40]. They also developed a lattice model with four metastable states that accurately reproduced the experimental data[23]. However, it is difficult to extract information at atomic resolution from this simple model.

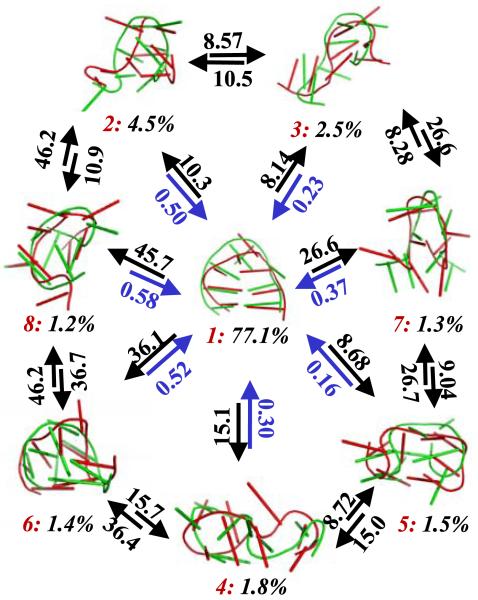
MSMs are a useful tool for extracting kinetics from atomistic simulations. From L3 MSM, we have computed the Mean First Passage Time (MFPT) between the eight most populated metastable states. The MFPT is defined as the average time taken to get from the initial state to the final state[41]. It can easily be computed from a transition probability matrix (see the Appendix B for details). The results of this calculation are displayed in Figure 6, along with representative structures from each state. State 1 is the folded state and has the largest population (77.1%), indicating the free energy surface is biased to the native state at 300K. Multiple non-native states, each directly connected to the folded state, are also identified: e.g. states 3 and 4 with coil structures, state 2 with a shifted base pairing, and state 5 with an unfolded loop. MFPTs for folding (i.e. transitions from non-native states to the folded state) are all around a few hundred nanoseconds, while MFPTs for unfolding are at least an order of magnitude longer (from a few to tens of microseconds). This confirms that the folded state is the most stable state at 300 K. All MFPTs between non-native states are at least eight microseconds, much longer than those for folding. This suggests that these states are uncoupled from each other. Therefore, no metastable on-pathway intermediate states are indentified in this system. The transition from state 1 (folded) to 8 (shifted base pairing) has the longest MFPT (45.7 microseconds) among all the unfolding transitions, indicating a large energy barrier for breaking non-native base pairing/stacking followed by forming native ones. State 5 (unfolded loop) has the shortest MFPT (0.16 microseconds) among all the folding transitions, which suggests the kinetics of loop rearrangements are relatively rapid.

Figure 6.

Mean First Passage Times (MFPTs) between the eight most populated states in the L3 MSM with a lag time of 20ns (L3 MSM is generated from a super level set with three levels, see Table 1 for details). All the MFPTs are in units of microseconds. States are labeled in red from 1 to 8 according to their populations in descending order. The populations of each state are shown in black. Two representative conformations are shown from each state using Pymol[42] with a cartoon representation. These conformations were extracted by selecting the centers of the top populated microstates in each macrostate.

We have successfully extracted kinetic information between the most populated metastable states from our MSMs. The overall unfolding timescales fall in a range of a few to tens of microseconds, in qualitative agreement with experimental observations. However, direct comparisons between our simulations and laser T-jump experiments are not possible at present because our simulations are at a single temperature and are therefore unable to capture effects due to the temperature jump. No stable thermodynamic intermediate states were found for folding of this 8 nucleotide RNA hairpin, in contrast to a previous study of a 12 nucleotide hairpin[22]. These results suggest that increasing the number of stem base pairs complicates the folding mechanisms of RNA hairpins.

4. Conclusions and Future Plans

Markov State Models (MSMs) are a useful tool for bridging the gap between experimental and computational timescales. MSMs are inherently multi-resolution, however, algorithms focused on constructing MSMs at different resolutions are lacking. Here we have introduced a new algorithm, called Super-level-set Hierarchical Clustering (SHC), which is capable of constructing MSMs of conformational dynamics at multiple resolutions. The key insight of this algorithm is to perform spectral clustering hierarchically using super level sets starting from the highest density level, which guarantees that highly populated metastable regions are identified before less populated ones. This is an improvement over direct application of spectral clustering to the full data set, which tends to identify sparse states that are very weakly coupled to the rest of phase space due to insufficient sampling before identifying real metastable states in denser regions of phase space. We applied SHC to an 8 nucleotide GCAA RNA tetraloop, and built four MSMs at different resolutions. Each of these models was validated by both the implied timescales and Chapman-Kolmogorov checks. The overall unfolding timescales predicted from our MSMs are between a few and tens of microseconds, which are qualitatively consistent with those observed by laser temperature jump experiments. Our results suggest that there are no metastable intermediate states. Instead, the folded state is directly connected to multiple unfolded and misfolded states, which all fold faster than they interconvert with one another.

In SHC, we use the populations of microstates from K-centers clustering to approximate their conformation density. However, estimating densities in high dimensional spaces is quite challenging. In particular, our approximate K-centers algorithm only generates clusters with approximately equal radii and small variances in the cluster radius may induce large volume differences. In the future, we plan to improve our density estimates by computing kernel density functions around microstate centers or the average of the kernel density for a few randomly selected conformations within the state. Alternatively, we may employ nonlinear dimensionality reduction techniques[32] to discover lower dimensional spaces where the density may be estimated more easily. We have demonstrated that SHC is able to generate a large number of MSMs at different resolutions. However, we haven’t discussed how to determine which one is the best model. A Bayesian approach to compare different MSMs by Bacallado et al.[43] may be used for model selection in the future. Finally, while we have focused on identifying metastable states in this work, SHC may also be used to identify intermediate and transition states by studying non-attractive nodes in lower density super density levels. In addition to being biologically relevant themselves, identification of these states could allow us to perform adaptive sampling by starting more simulations from transition states in order to rapidly sample transition events between metastable states.

Appendix A: Simulation Details

Our simulations were generated using the Adaptive Seeding Method (ASM)[31]. First, two sets of 1120 27ns Simulated Tempering (ST) simulations[29, 30] were run: one started from a folded state and the other from a random coil. An independent MSM with 10 states was then built using MSMBuilder[18] for each dataset in order to identify the dominant metastable states. Next, one hundred random conformations were selected from each metastable state and used as starting points for new constant temperature simulations (2,000 points in total). Five 45ns constant temperature 300K MD simulations were launched from each point. This resulted in a dataset with 9,963 trajectories (some simulations were not completed). All the simulations were performed using Stanford’s Bio-X² cluster and Folding@Home[44]. We used nucleic acid parameters from the AMBER99 force field[45, 46]. The RNA molecule was solvated in a water box with 2,543 TIP3P[47] waters and 7 Na⁺ ions. The simulation system was minimized using a steepest descent algorithm, followed by a 100ps MD simulation applying a position restraint potential to the RNA heavy atoms. All NVT simulations were coupled to a Nose-Hoover thermostat with a coupling constant of 0.02ps⁻¹[48]. A cutoff of 10 Å was used for both VdW and short range electrostatic interactions. Long-range electrostatic interactions were treated with the Particle-Mesh Ewald (PME) method[49]. Nonbonded pair-lists were updated every 10 steps with an integration step size of 2 fs in all simulations. All bonds were constrained using the LINCS algorithm[50].

Appendix B: Mean First Passage Time (MFPT)

The mean first passage time (MFPT) from initial state i to final state f in an MSM is the average time taken to get from state i to state f[41]. The MFPT (X_if) given that a transition from state i to j was made first is the time it took to get from state i to j plus the MFPT from state j to f. Thus the MFPT (X_if) can be defined as (cite),

$$X_{if}=\sum _j{P}_{ij}(t_{ij}+X_{jf})$$ (A.1)

where t_ij is the lag time of the transition matrix T. The boundary condition for this calculation is:

$$X_{ff}=0$$ (A.2)

The set of linear equations in Equation (A.1) and (A.2) can be solved to obtain the MFPT X_if.