Figure 11.

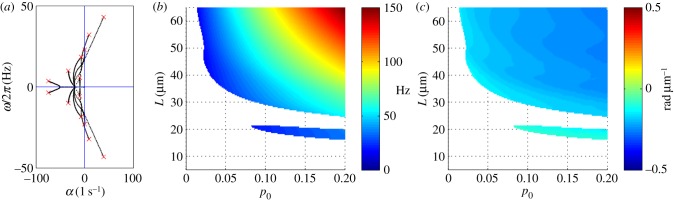
Eigenvalues of the GC model from the weighted residual method: (a) paths of eigenvalues σ = α + iω in the complex plane as p₀ is varied (0 < p₀ < 0.2) in the GC flagellar model (equation (3.31)). Other parameters are as in table 3. The red ‘x’ symbols denote the eigenvalues at the final value p₀ = 0.2. (b) Frequency ω/2π (Hz) of the least stable mode of the GC model as a function of flagellar length and baseline probability of dynein activation, p₀. Other parameters are as in table 4. At each parameter combination (p₀, L), frequency is obtained from the imaginary part (iω) of the eigenvalue σ = α + iω with largest real part (α). (c) Median phase gradient, 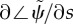, of the least stable mode. Anterograde (proximal–distal) propagation corresponds to a phase gradient <0, for ω > 0. For all parameter combinations shown, the least stable mode exhibits anterograde propagation.