Figure 2.

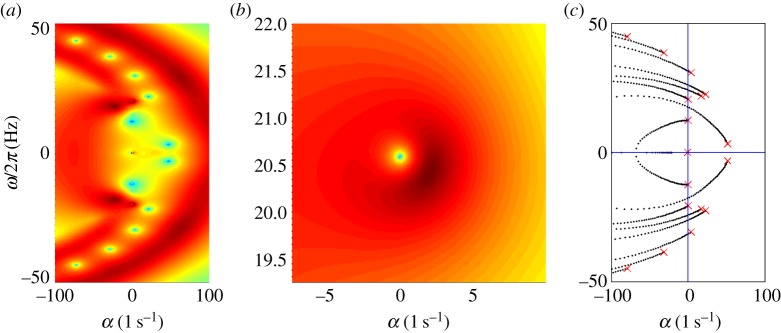
(a) Eigenvalues from the assumed exponential solution of the sliding-controlled flagellar model (equation (3.14)) with sliding permitted at the base (case 1; parameters in table 1). Images of the log magnitude of the determinant, ln|D(σ)| (arb. units), are shown as a function of σ = α + iω. Eigenvalues (characteristic exponents) are found at local minima (blue) of |D(σ)|. Unstable modes have α = Re(σ) > 0. (b) Expanded view of panel (a) shows the eigenvalue at σ = i2π · 20.6 corresponding to a 20.6 Hz periodic mode. (c) Eigenvalues from the weighted-residuals method: paths of eigenvalues σ = α + iω are shown in the complex plane as 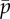is varied (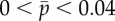). Other parameters are as in table 1. The red ‘x’ symbols denote the eigenvalues at the final value 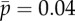. The eigenvalues in panel (c) closely match the minima of |D(σ)| in panel (a). (Online version in colour.)