Table 2.
Algorithm for the coupling of the compartment-based regime with the PDE-based regime in the case of high copy numbers.
| (i) | Initialize the time, t = t0 and set the final time, tfinal. Specify the PDE-update time step dtP and initialize the next PDE time step to be tP = t + dtP. |
| (ii) | Initialize the number of particles in each compartment in ΩC, Ai for i = 1, …, K, and the distribution of probability density in ΩP, p(x,t0), for x ∈ ΩP. |
| (iii) | Calculate the propensity functions for diffusion between the compartment regimes as αi,j = AiD/h2 for i = 1…K and j = M + 1, M + 2 and for reactions as αi,j for i = 1…K and j = 1, …, M using the usual mass action kinetics. |
| (iv) | Calculate the propensity function for diffusion from the pseudo-compartment, C−1, in ΩP into the adjacent compartment in 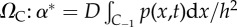 (equation (2.4)). (equation (2.4)). |
| (v) | Calculate the sum of the propensity functions,  . . |
| (vi) | Determine the time for the next ‘compartment-based’ event tC = t + τ, where τ is given by equation (2.2). |
| (vii) | If tC < tP then the next compartment-based event occurs: |
| (a) Determine which event occurs according to the method described in the text (see [48]). | |
(b) If the event corresponds to αi,j for i = 1…K and j = M + 1, M + 2 then move a particle from compartment i in the direction specified by j. If the particle crosses the interface into pseudo-compartment C−1 then add a particle's worth of mass to the region C−1 i.e.  . Here . Here 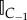 is the indicator function which takes the value 1 in C−1 and 0 elsewhere. is the indicator function which takes the value 1 in C−1 and 0 elsewhere. |
|
(c) If the event corresponds to propensity function α* and p(x,t) > 1/h forall x ∈ C−1 then place a particle in C1. Remove a particle's worth of mass from the PDE solution in the region C−1 i.e. 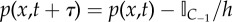 . . |
|
| (d) update the current time, t = tC. | |
| (viii) | If tP < tC then the PDE regime is updated: |
| (a) Update the PDE solution according to the numerical method described in §2.1.2 using p(x,t) as the previous value of the solution. | |
| (b) Update the current time, t = tP and set the time for the next PDE update step to be tP = tP + dtP. | |
| (ix) | If t ≤ tfinal, return to step (iii). |
| Else end. |
