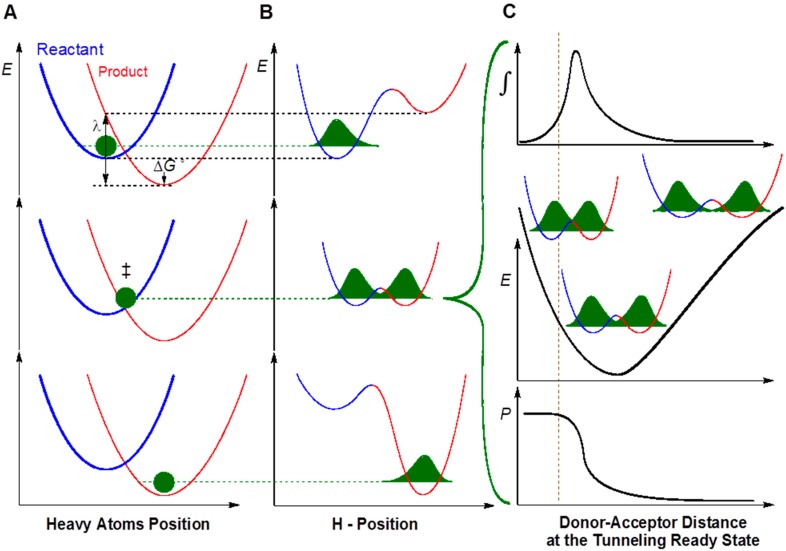
Figure 3.

An example of a model used to analyze kinetic isotope effects (KIE) for H-transfer reactions (sometimes called Marcus-like models). Three slices of the potential energy surface (PES) along components of the collective reaction coordinate showing the effect of heavy-atom motions on the zero point energy in the reactant (blue) and product (red) potential well. (A) Presents the heavy atom coordinate (also known as the Marcus parabolas); and (B) shows the H-atom position, which is orthogonal to the heavy-atom coordinate. In the top panels, the hydrogen is localized in the reactant well, and the zero point energy of the product state is higher than that of the reactant state. Heavy atom reorganization brings the system to the tunneling ready state (TRS, middle panels A and B), where the zero point energy in the reactant and product wells are degenerate and the hydrogen can tunnel between the wells. Further heavy atom reorganization breaks the transient degeneracy and traps the hydrogen in the product state (bottom panels). The rate of reaching the TRS depends on the reorganization energy (λ) and driving force (ΔG°), which are indicated in the top panel (see [24] for more details and equations); (C) shows the effect of Donor–Acceptor Distance (DAD) sampling on the wave function overlap at the TRS (middle panel). Transmission probability (P) is a function of the overlap integral of the hydrogen wave functions in the reactant (blue) and product (red) wells (bottom panel C). The top panel C presents the contribution to H-transfer at each DAD as a function of the P and the population at each DAD. The vertical dashed line represents the DAD under which the Zero Point Energy (ZPE) is greater than the barrier height. At such distances, the process of a wave function spreading from reactant well to product well is no longer “tunneling”, but one can still use the particle’s transmission probability analogously to the tunneling probability at longer DADs.