The solvent component of macromolecular crystals

On average, the mother liquor or solvent and its constituents occupy about 50% of a macromolecular crystal. Ordered as well as disordered solvent components need to be accurately accounted for in modelling and refinement, often with considerable complexity.

Abstract

The mother liquor from which a biomolecular crystal is grown will contain water, buffer molecules, native ligands and cofactors, crystallization precipitants and additives, various metal ions, and often small-molecule ligands or inhibitors. On average, about half the volume of a biomolecular crystal consists of this mother liquor, whose components form the disordered bulk solvent. Its scattering contributions can be exploited in initial phasing and must be included in crystal structure refinement as a bulk-solvent model. Concomitantly, distinct electron density originating from ordered solvent components must be correctly identified and represented as part of the atomic crystal structure model. Herein, are reviewed (i) probabilistic bulk-solvent content estimates, (ii) the use of bulk-solvent density modification in phase improvement, (iii) bulk-solvent models and refinement of bulk-solvent contributions and (iv) modelling and validation of ordered solvent constituents. A brief summary is provided of current tools for bulk-solvent analysis and refinement, as well as of modelling, refinement and analysis of ordered solvent components, including small-molecule ligands.

1. The solvent in macromolecular crystals  

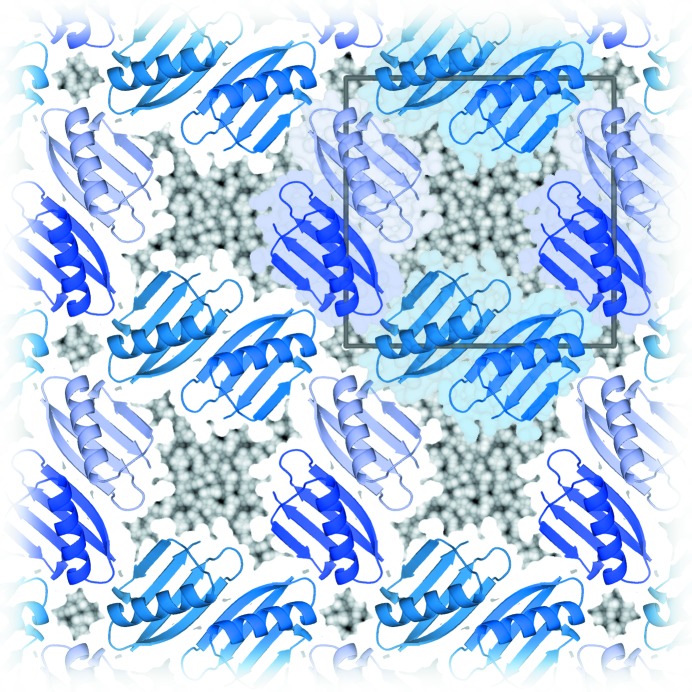
Crystals of proteins and other biological materials almost always grow in a drop of aqueous mother liquor containing a variety of reagents which promote the self-assembly of the irregularly shaped macromolecules into an ordered and regular crystal structure. This self-assembly during crystallo­genesis leads to an ordered network of molecules connected by few, but specific, weak noncovalent intermolecular interactions (Fig. 1 ▶). Given the irregular shape of protein molecules, it is not surprising that when they self-assemble into a crystal, substantial intermolecular space (on average approximately 50% of the crystal volume; Matthews, 1968 ▶) remains between the molecules, and it is filled with the mother liquor or crystallization cocktail from which the crystal grew. Much of this medium in the intermolecular space is disordered bulk solvent, and its content estimation and treatment in modelling and refinement are discussed in §2.

Figure 1.

Macromolecular crystals. Given favourable kinetics, macromolecules can self-assemble from a metastable, supersaturated solution into crystals, a periodic network of macromolecules connected by weak but specific intermolecular interactions. The solvent content V _S of this simple P ₄ crystal structure, PDB entry 2on8 (Wunderlich et al., 2007 ▶), is about 50%. The intermolecular regions are filled with dynamically moving solvent molecules, modelled as homogeneous bulk solvent §2.4. Its contributions to diffracted intensities are averaged over the entire molecule and over the time frame of a conventional diffraction experiment, with the dynamics of the solvent reflected in diffuse, non-Bragg scattering contributions. The region between the macro­molecules and bulk solvent may contain distinct solvent density which can be properly modelled as a part of the crystal structure. The complex and dynamic transition region from the ordered molecules to the bulk solvent is not separately modelled at present. This figure is in essence a modernised version of Figs. 1 in Bragg & Perutz (1952 ▶) and Moews & Kretsinger (1975 ▶).

The high solvent content in macromolecular crystals compared with solid-sphere close packing (where approximately 26% of the space is not occupied by spheres) on one hand limits the physical-mechanical stability of the crystals, but on the other does allow ions or small molecules to enter an already formed crystal through its solvent channels. Given that some components or additives of the mother liquor are chosen on the basis of their ability to mediate crystal contacts, it is also reasonable to expect that, in addition to ubiquitous water molecules, some of these special solvent components will form an integral part of the crystal structure. As ordered solvent molecules and ions, these components will exhibit distinctly visible electron density which must be modelled, refined and validated, as outlined in §3.

The analysis of crystal solvent content thus needs to consider a minimum of two major contributions to the data and the model: (i) the properties of disordered bulk solvent and (ii) the ordered solvent components displaying distinct electron density. A third intermediate region, the semi-ordered and in­homogeneous solvent, which often contains biologically relevant compounds such as lipids or membrane components, is not adequately described at present, which may be a contributing factor to the large gap observed between refinement R values and data quality (Holton et al., 2014 ▶).

For modelling and refinement, the simple binary and discontinuous ‘coordinates plus bulk solvent’ model does work reasonably well, although the dynamic nature of the macromolecule–solvent interface, as well as nonhomogenous solvent density, provide opportunities for methodological advances and better understanding of this biologically highly relevant and active interface region. In this review, we examine how to (i) estimate the overall solvent content of a macromolecular crystal, (ii) use this information to our advantage (for example in phase improvement), (iii) account for and model disordered bulk solvent and (iv) properly identify and model the distinct electron (or nuclear, in the case of neutron diffraction) density of ordered solvent molecules.

2. Bulk solvent  

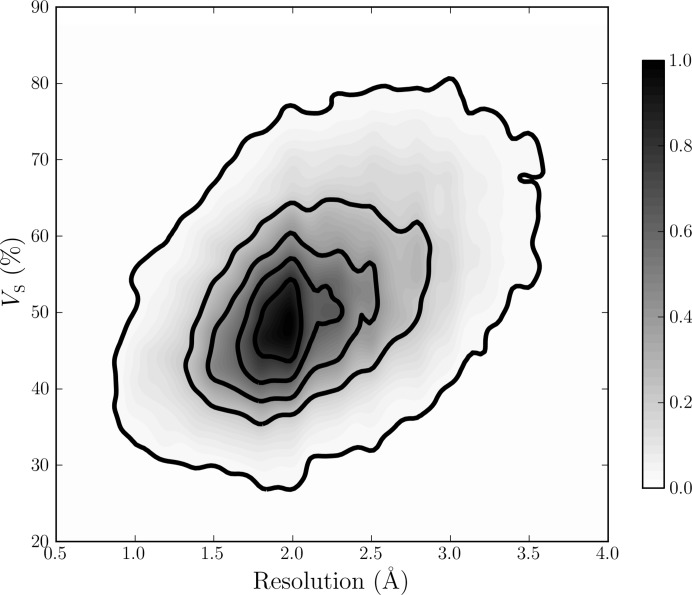
Shortly after about 100 crystal forms of globular proteins became available in the late 1960s, Matthews analysed the fractional volume of solvent in protein crystals (Matthews, 1968 ▶). His original estimate that on average close to half of the unit-cell volume is filled with mother liquor or solvent remains valid today. While the distribution of the solvent content peaks at around 50% of the crystal volume, the distribution is relatively broad, ranging from approximately the close-packing limit of 26% for spheres up to almost 90%, and in extreme cases even exceeding these limits in both directions; see Weichenberger & Rupp (2014 ▶) and Fig. 2 ▶. Knowing the solvent content of a biomolecular crystal generates useful information during the initial analysis of diffraction data (§2.1), and this knowledge is subsequently valuable in the phasing stage (§2.2 and §2.3). Proper modelling of the bulk-solvent contributions to the diffraction pattern is necessary for accurate reciprocal-space refinement of a crystal structure (§2.4).

Figure 2.

Two-dimensional density function of V _S for 60 218 protein crystal forms using binned two-dimensional kernel estimates. The scale of V _S from 20 to 90% on the y axis corresponds to V _M values between 1.54 and 12.3 ų Da⁻¹. The plot has been normalized to have a maximum value of 1. Isocontour lines are drawn as solid bold lines in increments of 0.2. There is a clear trend towards lower values of V _S at higher resolutions. Most density is centred about approximately 1.9 Å resolution and V _S = 50%, and typical values for V _S range between 30 and 80%. Figure from Weichenberger & Rupp (2014 ▶). Owing to a 60-fold lower number of available DNA/RNA crystal structures in the PDB, the dependence of experimental resolution on solvent content cannot be established for nucleic acid chains (see Supporting Information).

2.1. Estimating the unit-cell content  

The first step in the process of structure determination is almost always the estimation of the molecular unit-cell content, which can be performed as soon as the unit-cell dimensions and possible lattice types have been determined from indexed diffraction data. Solvent-content analysis often informs the choice of internal symmetry and point-group symmetry. Not only can the numbers of possible molecular entities fitting in the asymmetric unit cell be estimated, but highly improbable values of these numbers can indicate problems such as the presence of twinning, pseudo-symmetry or incorrect point (space) group assignment (Zwart et al., 2008 ▶). An accurate estimate of the solvent content is an important parameter in density-modification techniques (Hoppe & Gassmann, 1968 ▶; Barrett & Zwick, 1971 ▶; Bricogne, 1974 ▶; Zhang & Main, 1990 ▶; Podjarny et al., 1996 ▶; Zhang et al., 2001 ▶; Cowtan, 2010 ▶). Density modification is crucial in breaking the phase-angle ambiguity in single-wavelength anomalous diffraction phasing (Wang, 1985 ▶; Mueller-Dieckmann et al., 2007 ▶), for phase improvement (Abrahams & Leslie, 1996 ▶) and for phase extension (Sheldrick, 2010 ▶).

2.1.1. Matthews coefficient  

Based on an analysis of 116 different crystal forms of globular proteins (Matthews, 1968 ▶, 1976 ▶), Matthews observed that the fraction of the crystal volume occupied by solvent ranged from 27 to 78%, with the most common value being about 43%. Matthews further defined V _M, known as the Matthews coefficient, as the crystal (asymmetric unit) volume V _A per unit of protein molecular weight, M,

and showed that V _M bears a straightforward relationship to the fractional volume of solvent V _S in the crystal,

where the dimensions of the conversion factor 1.230 are Å⁻³ Da. The derivation of (2) was not explicitly provided in Matthews’ original publications, but it is elaborated in Weichenberger & Rupp (2014 ▶) together with a more complete compilation of historic and current overall solvent-content data.

2.1.2. Matthews probabilities: solvent content affects resolution  

Matthews realised that a relationship between the solvent content and the resolution of the diffraction data is plausible: tightly packed crystals with more contacts between individual molecules should be more stable and more ordered and possibly diffract better. Matthews’ intuitive prediction has been statistically verified using larger protein data sets, and a conditional probabilistic estimate for possible unit-cell contents as a function of resolution, termed the Matthews probability (MP), has been developed (Kantardjieff & Rupp, 2003 ▶). The MATTPROB web applet, the corresponding probability distribution function and its parameters for cumulative resolution bins have been provided to the crystallographic community, and the original MP estimator has been implemented in some form in the major crystallographic structure-determination packages [MATTHEWS_COEF in CCP4 (Winn et al., 2011 ▶), Phaser (McCoy et al., 2007 ▶) and PHENIX (Adams et al., 2010 ▶)]. A recent update of MATTPROB (Weichenberger & Rupp, 2014 ▶) employs a nonparametric kernel density estimator (http://www.ruppweb.org/mattprob/) which, by calculating the Matthews probabilities directly from empirical solvent-content data, avoids the need to revise the multiple parameters of the original binned empirical fit function presented in Kantardjieff & Rupp (2003 ▶). This updated analysis further reinforced the idea that solvent content and resolution are highly correlated. Modifications of the specific density for low-molecular-weight proteins (Quillin & Matthews, 2000 ▶; Fischer et al., 2004 ▶) have no practical effect on solvent-content prediction, and there is no correlation with oligomerization state (Chruszcz et al., 2008 ▶; Weichenberger & Rupp, 2014 ▶). While a weak, in practice irrelevant, dependence on symmetry and molecular weight was found, it cannot be satisfactorily explained using simple linear or categorical models.

A distinct feature of the Matthews probability is the implicit assumption of a Bayesian prior that the observed resolution represents only an empirical lower limit for the resolution. In other words, a crystal diffracted under certain experimental circumstances to at least the reported resolution, but in principle it could have diffracted better. The assumption of this Bayesian prior is also compatible with the fact that the distribution of reported resolution cutoffs is distinctly skewed towards cutoff values higher than the common mean I/σ(I) of 2.0 (Weichenberger & Rupp, 2014 ▶; Luo et al., 2014 ▶). At present, no agreement on objective criteria exists for the non­trivial selection of a resolution cutoff for model refinement, but it seems that commonly applied resolution cutoffs in fact under-report the actual diffraction potential of the crystals (Diederichs & Karplus, 2013 ▶; Luo et al., 2014 ▶).

2.2. Solvent in phasing: electron-density modification and masking  

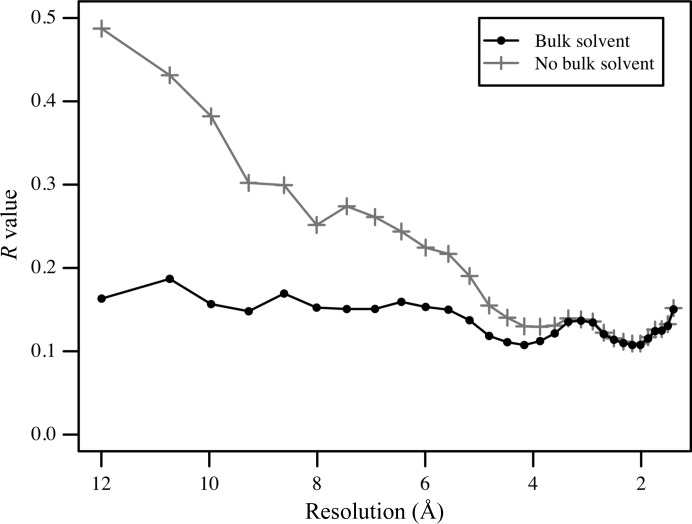
Disordered bulk solvent constitutes a rather substantial amount of scattering matter in a macromolecular crystal. Despite the bulk solvent not being structured, its average electron density in a crystal is still periodic and therefore it contributes to the Bragg reflections. The resulting bulk-solvent contribution to the structure factors is not the same across the entire resolution range, but varies from almost negligible at high resolution to quite significant at resolutions lower than approximately 6–8 Å (Fig. 3 ▶). The effect of bulk-solvent contributions on observed structure-factor amplitudes and the possibility of deriving the approximate molecular shape from their systematic change with bulk-solvent density was recognized and used by Bragg & Perutz (1952 ▶).

Figure 3.

Example of the bulk-solvent contribution to the R value shown by resolution for PDB entry 3fo3 (Trofimov et al., 2010 ▶). Solid black and grey curves show the effect of including (lower R values) versus not including (higher R values) the bulk-solvent contribution to the total model structure factors.

One of the most significant benefits of the large solvent content in protein crystals is that the difference between protein electron density and that of the surrounding bulk solvent provides the basis for exceptionally powerful phase-improvement techniques. In addition to handedness ambiguity of the heavy-atom solution, single anomalous diffraction (SAD) phasing experiments (Dauter et al., 2002 ▶; Mueller-Dieckmann et al., 2007 ▶; Read & McCoy, 2011 ▶) often have poor (centroid) starting phases as a consequence of the inherent phase-angle ambiguity. Such poor starting phases would not be routinely useable without the benefit of density modification for phase improvement and phase extension. Such methods were pioneered by Wang (1985 ▶), have been steadily improved (see, for example, Bricogne, 1984 ▶; Abrahams & Leslie, 1996 ▶; Podjarny & Urzhumtsev, 1997 ▶; Terwilliger, 2000 ▶; Zhang et al., 2001 ▶; Cowtan, 2010 ▶) and have been implemented in various forms in almost all macromolecular crystallographic structure-solution (i.e. phasing) software.

2.3. Delineation of atomic model and bulk solvent  

The idea behind most real-space-based phase-improvement methods (a.k.a. density modification) is in principle simple: make a (poor) initial electron-density map look more like a ‘real’ protein electron-density map1. A high solvent content is beneficial for density modification (phase improvement), because the description of a large bulk-solvent area as flat, continuous electron density is in fact a reasonable approximation of reality. A high solvent content therefore means that a large part of the crystal content is well described, and this is knowledge that comes into our hands essentially for free. Solvent flattening-based density-modification methods generally work better with higher solvent contents and perform poorly below 30%, where the solvent content essentially approaches the void volume of close-packed spheres, and the ratio of correctly described flat solvent versus poorly described partially ordered transition area decreases. In addition, high solvent contents benefit density modification following SAD phasing because the map noise (or when the substructure is centrosymmetric, the inverted image of the structure; see Table 10-2 in Rupp, 2009 ▶) can be better distinguished from the correct electron density. The various density-modification and phase-improvement methods have been reviewed, for example, in Podjarny et al. (1996 ▶), Rupp (2009 ▶) and Cowtan (2010 ▶) and in additional references provided below. The role and application of density modification and density averaging in the ab initio phasing of virus crystal structures has been reviewed separately by McPherson & Larson (2015 ▶).

2.3.1. Solvent flattening  

Common to the real-space-based methods is that a delineation is made between what is believed to be solvent and the parts of the map which might represent the protein model. In solvent flattening, a solvent mask (see §2.4.3) is generated within which the density is constant and belongs to bulk solvent (0.33 e Å⁻³ for pure water), and outside the mask protein is assumed (which has a higher average density of approximately 0.44 e Å⁻³). The phases generated from map inversion with the solvent region set to the flat density value then are used to improve the phases of the entire electron-density map, the solvent mask is updated and the process is iteratively repeated until convergence (Bricogne, 1974 ▶; Kleywegt & Read, 1997 ▶; Podjarny et al., 1987 ▶).

2.3.2. Solvent flipping  

The related technique of solvent flipping (Abrahams & Leslie, 1996 ▶) does not set the density values in a solvent region to a constant low value, but rather flips (i.e. changes the sign of) the grid point (or density voxel) values in the solvent region. Flipping the solvent density introduces independence between the partial maps, and thus allows unbiased phase probability combination. The powerful solvent-flipping procedure has been implemented, for example, in the program SOLOMON available in CCP4 (Winn et al., 2011 ▶) and as part of AutoSHARP (Vonrhein et al., 2007 ▶) and PHENIX (Adams et al., 2010 ▶).

2.3.3. Sphere of influence  

Flipping of density voxels that are unlikely to represent protein-atom sites is also an essential component of the SHELXE Sphere of Influence (SoI) algorithm (Sheldrick, 2010 ▶). In contrast to the binary methods that essentially integrate over the volume of a Wang sphere, SoI calculates the variance of the density on the surface of a 2.42 Å sphere. The reason for this choice of radius is to maintain some plausible chemical information: 2.42 Å is in fact the dominant 1–3 atom distance in proteins and nucleic acids. The covered density region is then split into solvent, macromolecule and a crossover region (Sheldrick, 2002 ▶). The variable (fuzzy) crossover region prevents the solvent mask from becoming locked in owing to an incorrect initial solvent-content estimate. Furthermore, the fuzzy region allows a smooth transition from solvent to protein. The final phase combination uses σ_A-weighted maximum-likelihood coefficients (Read, 1986 ▶), which reduce the partial bias from the parts of the map assigned as protein. The procedure is then repeated until convergence.

2.3.4. Boundary-region complexity  

The dynamic boundary layer surrounding a macromolecule in its solvent environment is in all likelihood incompletely described by a discontinuous binary transition in a ‘coordinates plus bulk solvent’ model. Efforts to use a smoothly changing continuum boundary (Fenn et al., 2010 ▶) have led to algorithmic advances, but no significant improvements in R values have been achieved. The indications are that the large gap between the R values observed in refinement of macromolecular structures at typical resolutions (R values of ∼20–30%) and the precision with which data are measured (R _merge of ∼4–7% on I) may originate at least partially from an inadequate description of the true electron density (Holton et al., 2014 ▶). Because the zone between the dynamically moving bulk solvent and the macromolecule is also the area where interesting interactions actually take place, one can expect that better modelling of and accounting for this boundary region will also improve the understanding of the associated biological phenomena.

2.4. Bulk-solvent refinement  

The bulk-solvent contribution to Bragg reflections originating from periodic bulk solvent is not the same across the entire resolution range, but instead varies from almost negligible at high resolution to rather strong at low resolution (Fig. 3 ▶). At low resolution, the contributions of the atomic model and bulk solvent at low resolution are comparable in magnitude but are opposite in phase. As a consequence, uncorrected model-only calculated structure factors are too large, and correspondingly higher R values result upon refinement without bulk-solvent correction; see the figures in Kostrewa (1997 ▶), Fokine & Urzhumtsev (2002b ▶) and Afonine & Adams (2012 ▶).

For the first few decades of protein crystallography, it was common practice to truncate the low-resolution data in refinement simply owing to the lack of a proper bulk-solvent model. Unfortunately, missing data, especially high-intensity low-resolution reflections (sometimes as few as 5%) can significantly deteriorate the quality of crystallographic maps (Lunin, 1988 ▶; Urzhumtsev et al., 1989 ▶; Cowtan, 1996 ▶; Urzhumtseva & Urzhumtsev, 2011 ▶), adversely impact crystallographic structure refinement (Kostrewa, 1997 ▶) and limit the success of molecular replacement (Fokine & Urzhumtsev, 2002a ▶).

2.4.1. Bulk-solvent models  

Because reciprocal-space refinement of a crystal structure model minimizes a likelihood target function derived from a sum of squared residuals between observed (F _obs) and calculated model structure-factor amplitudes (F _model), the bulk-solvent contribution F _bulk needs to be accounted for during the refinement of a crystal structure. For the purpose of reciprocal-space refinement, a physical model describing the entire crystal structure is needed, from which in turn model structure factors can be calculated. Such a model contains in general (i) atomic model parameters (parameters that describe coordinates, displacements etc. of specific atoms) and (ii) non-atomic model parameters that describe everything else such as bulk-solvent contributions, twinning fractions, various scales, overall anisotropy etc.). The complete model of a crystal structure in reciprocal space can then be represented in a generalized form by the total model structure factor (F _model) consisting of contributions from the individual atoms in the model (F _atoms) and the disordered bulk solvent (F _bulk) (Moews & Kretsinger, 1975 ▶; Afonine et al., 2012 ▶),

with the corresponding scales and components determined as described, for example, by Afonine et al. (2013 ▶) and Murshudov et al. (2011 ▶).

Currently, two major bulk-solvent models are in use in macromolecular crystallographic studies to calculate F _bulk(h):

• (i) the exponential (Babinet) bulk-solvent model based on Babinet’s principle, where a solvent contribution proportional but with the opposite phase of the protein contributions (that is with a negative sign) is added to the atomic model scattering contributions (Moews & Kretsinger, 1975 ▶; Tronrud, 1997 ▶); and

• (ii) the mask-based, flat bulk-solvent model, where the solvent contribution is accounted for as a partial structure contribution from a homogeneous, masked bulk-solvent region (Phillips, 1980 ▶; Jiang & Brünger, 1994 ▶). Although earlier refinement programs such as EREF (Jack & Levitt, 1978 ▶) and early versions of TNT (Tronrud, 1997 ▶) included masked bulk model options, they were nontrivial to use and were computationally very expensive at the time.

2.4.2. Exponential (Babinet) bulk-solvent model  

Because Babinet’s principle (see Sidebar 11-7 in Rupp, 2009 ▶) only holds for uniformly scattering objects, the exponential bulk-solvent model2

is strictly valid only for the correction of low-resolution reflections, but it is still effective to about 6 Å (Tronrud, 1997 ▶; Podjarny & Urzhumtsev, 1997 ▶; Glykos & Kokkinidis, 2000 ▶). In the exponential model, the only adjustable parameters are k _sol, the so-called contrast, a term first coined by Bragg & Perutz (1952 ▶) and defined as the ratio of the mean solvent electron density and mean protein electron density (∼0.76), and B _sol, a high attenuation factor (∼125–200 Ų) affecting the extent of the bulk-solvent contribution. As the highly attenuated solvent contribution is subtracted from the protein structure factors, the exponential model is most effective at low resolution. The Babinet model does not need a mask, and Babinet scaling can therefore be applied to compute improved scale factors before molecular-replacement searches, as implemented, for example, via improved σ_A estimates in the molecular-replacement likelihood functions in Phaser (McCoy et al., 2007 ▶; McCoy, 2007 ▶).

The Babinet-based model is available in the refinement programs SHELXL (Sheldrick, 2008 ▶) and BUSTER-TNT (Tronrud, 1997 ▶; Blanc et al., 2004 ▶) and in REFMAC, where it also can be used in combination with the flat solvent model (Murshudov et al., 2011 ▶).

2.4.3. Flat (masked) bulk-solvent model  

The flat or masked solvent model

or more generally, as described in Moews & Kretsinger (1975 ▶) and Afonine et al. (2013 ▶),

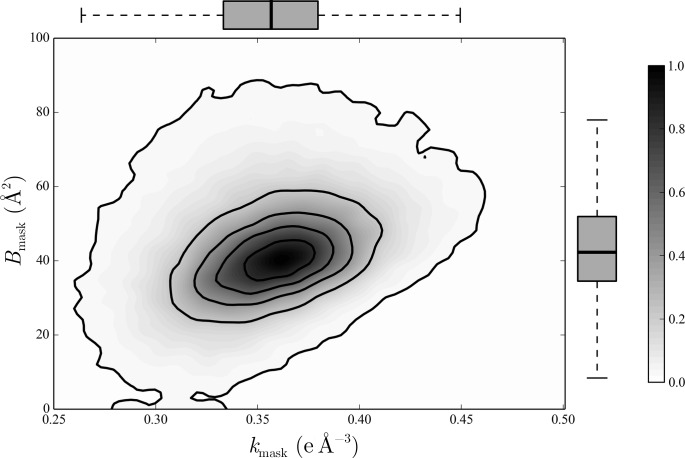
is presently the default choice to account for bulk solvent in macromolecular crystallographic studies. F _mask is the contribution from a homogeneous, masked bulk-solvent region. The physical meaning of the bulk-solvent parameter k _mask in the flat mask-based model is different from the interpretation of k _sol in the Babinet model (§2.4.2): in the flat mask model k _mask is the mean solvent electron density in e Å⁻³, while the Babinet k _sol is the contrast (ratio) between solvent and protein electron density. Both B _sol and B _mask are smearing (attenuation) factors in Ų which describe how deeply (on average) the bulk-solvent and macromolecular regions interpenetrate (Fokine & Urzhumtsev, 2002b ▶). Owing to the presence of an already defined mask boundary region, B _mask, with a mean of 42 Ų, is significantly smaller than B _sol (Fig. 4 ▶). Depending on the refinement program, additional mask-generation parameters such as the solvent probe radius extending the solvent boundary beyond the van der Waals surface of the protein and a back-fill probe (shrink) radius determining the penetration of the solvent back into the gap between the protein surface and solvent boundary can be optimized in the flat bulk-solvent model (Richards, 1985 ▶; Jiang & Brünger, 1994 ▶; Kostrewa, 1997 ▶).

Figure 4.

Bulk-solvent parameters. Two-dimensional density function of the bulk-solvent parameters k _mask/B _mask derived from 70 481 entries deposited in the PDB for which refinement data could reliably be extracted. Values for the mean solvent density k _mask and smearing factor B _mask were computed with PHENIX (Adams et al., 2010 ▶). The plot is limited to PDB entries with R _work between 0.05 and 0.30, only positive values for k _mask, measurements of B _mask of less than 300 and a solvent content of at least 5%. The density function was constructed using a two-dimensional kernel density estimation with an axis-aligned bivariate normal kernel and has been normalized to a maximum value of 1. Isocontour lines are plotted as solid lines at regularly spaced intervals of size 0.2. Box plots show the extents of the k _mask and B _mask distributions; the median is indicated by a thick line in the grey box, which represents the interval from the lower to the upper quartile, and whiskers extend to data points not more extreme than 1.5 times the interquartile range. The sample median of k _mask equals 0.36 (0.04) e Å⁻³ and for B _mask the sample median is 42.4 Ų. The distribution of B _mask has a small tail towards higher values, which is expressed by its sample skewness of 3.2, whereas the k _mask distribution appears to be much more symmetric about its mean, with a sample skewness of 0.43. This plot does not show 2.7% of B _mask entries and 1.7% of k _mask data, which are located outside of the limits of the axes. This figure was generated with matplotlib (Hunter, 2007 ▶).

The flat solvent model is available in programs such as CNS (Brünger et al., 1998 ▶), PHENIX (Adams et al., 2010 ▶) and REFMAC, which also allows the flat masked solvent model to be combined with a modified exponential Babinet model (Murshudov et al., 2011 ▶). CNS uses an improved flat model that incorporates grid searches for solvent parameters as suggested by Fokine & Urzhumtsev (2002b ▶) to improve convergence. CNS also refines the parameters involved in mask calculation such as solvent and shrink-truncation radii (Brunger, 2007 ▶). PHENIX uses an even more enhanced flat solvent model in which the solvent parameters are calculated analytically and simultaneously with all of the other scale parameters such as overall anisotropic scaling and twin fraction, making this method fast and independent of minimizer convergence (Afonine et al., 2013 ▶). Other enhancements to the flat solvent model that address discontinuity at the solvent–macromolecule boundary have been proposed (Fenn et al., 2010 ▶). In some cases the distribution of bulk solvent may be naturally non-uniform across the volume of the unit cell (Burling et al., 1996 ▶; Sonntag et al., 2011 ▶). In these cases the simple flat mask model may not be sufficient and better models that would account for distinguishable differences in the bulk-solvent region will have to be developed.

2.4.4. Physical meaning of solvent parameters  

In a simple and most used case (except for PHENIX, where the parameterization is different; for details, see Afonine et al., 2013 ▶), the two adjustable parameters (apart from mask calculation parameters) of the flat bulk-solvent model have a clear physical meaning and predictable values (Fokine & Urzhumtsev, 2002b ▶): the mean solvent density k _mask (e Å⁻³) and a smearing factor B _mask (Ų) which describes how deeply (on average) the bulk-solvent and macromolecular regions interpenetrate. Because these two parameters are good indicators of data and model quality, they are useful criteria for the validation of new structures or checking the consistency of existing entries (for a systematic study, see, for example, Afonine, Grosse-Kunstleve et al., 2010 ▶). Unusual values of these parameters may indicate serious problems with the data, model or refinement. Typically, k _mask approaching zero means no bulk-solvent contribution (which is highly improbable) and may indicate serious problems with the model, the data or both (Janssen et al., 2007 ▶; Rupp, 2012 ▶).

2.4.5. Bulk-solvent correction caveats  

Mask-based bulk-solvent models can produce (difference) electron-density map artefacts depending on the choice of the parameters describing the mask surrounding the macromolecule. Examples include the following.

• (i) If the mask around the protein and/or the associated shrink radius are selected so that the protein mask intrudes into true bulk solvent (i.e. no bulk solvent density is calculated in these solvent regions), the resulting electron-density difference map will show positive peaks or ‘blobs’ for the missing bulk-solvent density, which might be misinterpreted as ordered solvent components.

• (ii) When unmodelled protein density is assigned as solvent, a background of solvent density will be calculated there, reducing the positive difference density of any ordered protein features.

• (iii) If the protein mask excludes channels that are in fact empty but large enough so that the mask probe can enter them, they are mistakenly assigned as bulk-solvent density, resulting in negative electron-density difference map peaks.

Precautions against such artefacts include cavity-detection algorithms that eliminate holes inside a protein mask (Murshudov et al., 2011 ▶) or the introduction of an additional, unmodelled protein density contribution (Blanc et al., 2004 ▶) in the refinement.

Comparing maps obtained from the application of the masked, flat bulk-solvent model with those obtained using the exponential Babinet bulk-solvent correction can serve as a control if solvent correction-induced artefacts are suspected. The Babinet model differs from the flat mask model in two crucial aspects. The high effective attenuation (B ≃ 125–200 Ų) restricts the effect of the Babinet correction to low-resolution data, keeping the remaining high-resolution reflections (and the overall scaling dominated by them) unaffected. In addition, in the Babinet model anything that is not part of the modelled protein (F _atoms) is automatically and implicitly assigned as solvent, eliminating local masking bias. As a consequence, situation (i) described above, for example, is not possible: anything not assigned as protein is treated as belonging to solvent, leading to a situation similar to that described in (ii) but likely less dramatic. Although the effects of incorrect modelling of protein versus solvent are in principle similar in the Babinet model, the type and severity of the errors that can be introduced are limited. Ultimately, better methods to define, refine and update mask parameters, probably combined with a better description of disordered protein regions (see Blanc et al., 2004 ▶), or even more complex transition regions, need to be developed to address solvent correction-induced artefacts in electron-density reconstructions.

2.5. Diffuse scattering  

In contrast to the periodically present solvent density in the crystal that contributes to Bragg reflections, thermal diffuse scattering (TDS) arises from temporal and spatial disorder in the lattice [with additional diffuse scattering contributions to the recorded diffraction pattern originating from Compton scattering of the entire object(s) in the X-ray beam, not just the crystal]. Any deviation from the periodicity in the crystal lattice, including variation in the solvent density and not limited to disorder introduced by atomic displacements, causes variation in the periodicity of the electron density of a crystal and gives rise to diffuse scattering. Bragg spots reflect the time-averaged structure, while diffuse scattering contributions to the diffraction pattern provide a measure of the dynamic motions or deviations within the crystal (Clarage & Phillips, 1997 ▶). TDS can therefore provide a window into the dynamics of biological macromolecules. The advance of high-speed data collection with pixel-array detectors (PADs) and the potential to take advantage of the time structure of free-electron laser (FEL) X-ray sources have renewed interest in TDS analysis of proteins (Wall et al., 2014 ▶).

3. Ordered solvent components  

Solvent components which have become ordered in the crystal lattice contribute to Bragg scattering and their electron-density reconstruction will display distinct features, allowing them to be modelled as part of the atomic structure model. Their identification is often nontrivial because their electron density may not be unique (NH₄ ⁺, Na⁺ and Mg²⁺, for example, are isoelectronic with water), and more often than not, the composition of the crystallization cocktail, chemical plausibility, charge complementarity, local environment, coordination geometry and stereochemistry provide additional and crucial clues about their identity (Table 1 ▶). Additional complications arise from the possibility of partial occupancies (which are not restrained to sum to 1.0, as is the case, for example, for multiple side-chain conformations) and from the fact that moieties possessing symmetry can be located on corresponding special positions that share the same or higher symmetry than the object. At typical macromolecular resolution, electron-density features representing water molecules or single ions appear spherical and they can be located on any special position. Small-molecule ligands or cofactors often possess symmetry compatible with crystallographic symmetry operations and can be located on corresponding special positions. Alternate partial occupancies of ligands on special positions such as twofold axes are also possible and are not uncommon. Because water molecules or ions are not as strongly bound as, for example, covalently connected side-chain atoms in a protein molecule, their B factors are not tightly restrained and can be significantly higher than those of the neighbouring protein atoms. Complicating matters further, although the resulting electron-density distributions are theoretically different, the distinction between low occupancy versus high B factor of an atom is not clear at the resolution of most protein structures.

Table 1. Common constituents of intermolecular solvent space.

CC, crystallization cocktail; PS, protein stock solution; S, soaking solution; LCP, lipid cubic phase. Evaluation of electron-density shape in combination with coordination distances and geometry as well as plausible environment and molecular pose in the case of ligands aid in the identification of ordered solvent components.

Solvent component	Common source	Geometry	Electron density
Water	CC, PS	Single, tetrahedral, five- and six-membered rings, networks	Spherical, can be on any special position
Buffer	CC, PS	Molecular shape, e.g. tetrahedral (SO4 2, PO4 3), some zwitterionic etc.	Molecular shape, sometimes only parts visible
Metal ions, anions	CC, PS, S	Varying typical distances/environments, often octahedral	Spherical, higher density value according to Z, can be on any special position
Ligand	CC, S	Molecular pose, specific contacts	Molecular shape, sometimes only parts visible
Cofactor	CC, PS, S	Molecular pose, specific contacts, some covalent (e.g. PLP)	Molecular shape, sometimes only parts visible
Other precipitant	CC	According to molecule (e.g. glycerol, cryo-buffer)	Molecular shape, sometimes only parts visible
Lipid	PS, LCP	Tail in hydrophobic environment, head polar	Molecular shape, sometimes only parts visible
Detergent	CC, PS	According to molecule, some zwitterionic	Molecular shape, sometimes only parts visible

3.1. Water molecules  

In its natural environment, a protein is surrounded by and interacts with a wide variety of other moieties, and a large part of this molecular environment consists of water molecules. The physicochemical properties of the surface amino acids of the protein impose a dynamic hydration shell of one or two layers of ordered water molecules around the protein (Fogarty & Laage, 2014 ▶), which contribute to the measured X-ray diffraction intensities and therefore must be included in the structure model. Electron density of water molecules can be readily identified by spherical 2mF _o − DF _c and/or mF _o − DF _c Fourier maps located at a hydrogen-bond distance from hydrogen-bond acceptors or donors. Only in ultrahigh-resolution electron-density maps (resolution better than ∼1.0 Å) or neutron diffraction nuclear density maps (Afonine, Mustyakimov et al., 2010 ▶) can individual H atoms be clearly discerned.

3.1.1. Hydrogen-bond networks  

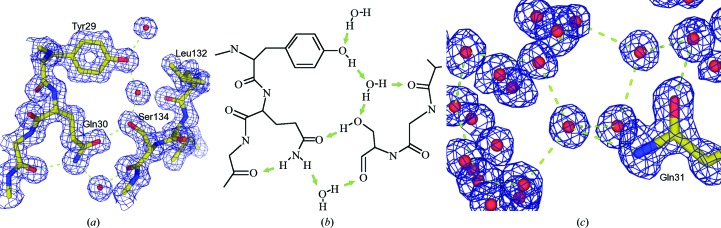
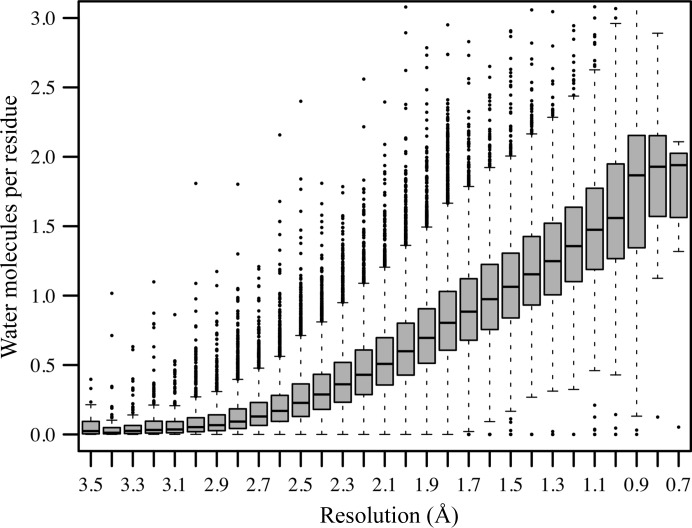
Owing to their polarity, water molecules are highly versatile hydrogen-bond donors and acceptors. A single molecule can donate two hydrogen bonds through its covalently bound H atoms and can accept two hydrogen bonds via the two lone pairs of electrons on its oxygen, resulting in a total of four hydrogen bonds. The hydrogen-bond network of modelled water molecules needs to make corresponding chemical sense, and a network of tetrahedrally coordinated water molecules and five-ring or six-ring assemblies can often be observed (Fig. 5 ▶). The number of water molecules that can be identified and built depends on the molecular structure, but in general more ordered water molecules can be placed at higher resolution (Fig. 6 ▶).

Figure 5.

Extended hydrogen-bonded water networks. (a) presents a well defined hydrogen-bond network found in PDB entry 2j9n (Viola et al., 2007 ▶). The blue mesh represents the contours of σ_A-derived maximum-likelihood 2mF _o − DF _c maps at the 1σ level, and the green arrows in the chemical scheme shown in (b) point towards the hydrogen-accepting electron lone pairs. Note that each bond has a proper donor–acceptor pair (which clearly defines the proper orientation of the Gln30 residue) and the different types of interactions: direct backbone–side chain, side chain–side chain and water-mediated interactions between residues. Typical X—O—H angles are 120° for the sp ²-hybridized orbitals of the –OH groups and 104.5° for H—O—H in the nearly tetrahedrally coordinated water O atom. The covalent O—H distance is 0.96 Å. (c) depicts a well defined water network in the intermolecular space of a high-resolution (1.2 Å) structure revealing typical, ice-like five-membered and six-membered water-ring networks, while the central water atom possesses an almost perfect tetrahedral arrangement of hydrogen-bond partners (PDB entry 1bpi; Parkin et al., 1996 ▶; figure adapted from Rupp, 2009 ▶).

Figure 6.

Resolution-dependent mean number of water molecules per amino acid. The mean number of water molecules per residue is computed as the number of water molecules divided by the number of amino acids of all chains present in the asymmetric unit. This number was computed for each of the 77 346 protein structures determined by X-ray crystallo­graphy downloaded from the PDB on 23 May 2014. The figure utilizes box plots to visualize the distribution of the number of water molecules per residue observed in 0.1 Å bins in the experimental resolution range 0.6–3.5 Å. In the box plot, the grey boxes display values that fall in between the first and third quartile, the black bar represents the median and the whiskers extend to data points no more than 1.5 times the inner quartile range; data points outside this region are highlighted as black dots. The graph reflects the plausible trend that more discrete waters can be built in structures with higher resolution than in those with lower resolution. In the low-resolution range the distributions are skewed towards zero water molecules per residue, as can be read from the location of the median in these distributions. This trend holds until resolutions as low as 2.5 Å, from where on the distributions start to become symmetric. Notice that the bins for very high (better than 0.8 Å) and very low (worse than 3.3 Å) resolution are populated with fewer than 100 measurements. A corresponding plot for nucleic acid structure models displaying similar but limited information owing to the much smaller number of DNA/RNA structures determined by X-ray crystallo­graphy is provided in Supplementary Fig. S2.

Because H or D atoms have significant neutron scattering factors (the former with a negative sign but significant background scattering) comparable with those of the heavier atoms, water networks and protonation states can be often assigned in nuclear density. PHENIX provides the option for separate or combined X-ray/neutron refinement (Afonine, Mustyakimov et al., 2010 ▶).

3.1.2. Automated water building  

Almost all major crystallographic packages and model-building programs have been furnished with automated water-picking and analysis procedures. In the CCP4 (Winn et al., 2011 ▶) program suite, REFMAC (Murshudov et al., 2011 ▶) is coupled with calls to arp_waters (Lamzin & Wilson, 1993 ▶), which removes atoms that do not fit into the electron density and places new water atoms into unoccupied electron-density peaks under the consideration of various distance criteria. The phenix.refine program (Afonine et al., 2012 ▶) provides a command-line option for water picking (ordered_solvent) and SHELXL (Sheldrick & Schneider, 1997 ▶) provides the program SHELXWAT for ‘automated water divining’ based on the ARP/wARP procedure (Lamzin & Wilson, 1993 ▶). The CNS refinement protocols (Brunger, 2007 ▶) provide input files for water placement and removal. In general, these programs follow the same strategy as a human model builder: waters are selected by a peak search in the difference electron-density map. Additional constraints ensure that the putative water molecule is at a hydrogen-bonding distance from protein atoms or other water molecules and that it is realistically close to the protein, manifesting a reasonable hydration-shell model. In the presence of noncrystallographic symmetry (NCS), the CCP4 program WATNCS uses this information to remove waters that do not follow the NCS constraints, whereas WATERTIDY can be seen as a post-processing step after water picking that moves symmetry-related waters close to the protein chain and attempts to establish sensible hydration shells. The popular interactive model-building program Coot (Emsley et al., 2010 ▶) combines water picking and water-molecule analysis with real-space validation.

Recent developments in program packages such as PHENIX have led to much improved ‘water’-divining procedures (Echols, Morshed et al., 2014 ▶) which are able to discern water molecules from other ions based on a number of electron-density, refinement and plausibility criteria, as detailed in §3.2.

3.1.3. B factors and occupancies of ordered water molecules  

After refinement, it is worthwhile taking a critical look at the B factors of modelled water molecules, which are highly variable and depend on the local environment. Water molecules are not linked by covalent bonds to other atoms, and they become increasingly more mobile with increasing distance from the protein. While the B factors of such water molecules can be considerably higher than the B factors of neighbouring protein atoms, closely bound water molecules in a stable hydrogen-bond network with protein atoms, which de facto provides a restraint on increasing displacement or mobility, will in general have B factors that are not much higher than their environmental neighbours.

3.1.4. High B-factor water molecules  

With increasing distance from the ordered protein surface, displacement and mobility generally increase and, correspondingly, electron-density peaks will become wider and lower and refined B factors will increase. Very high B factors are often associated with spurious water molecules, and any density that has no sensible noncovalent interaction of less than 4–5 Å with other moieties is hard to justify using a simple water model. While significant positive difference density should be explained when possible, indiscriminately placing water molecules into each and every positive difference density creates a non­parsimonious model (Dauter et al., 2014 ▶) that is overfitted and often has inferior R _free values (Brünger, 1992 ▶) or larger R–R _free gaps (Tickle et al., 2000 ▶) than a simpler, plausible model. Similar considerations hold for water molecules uncritically placed in density peaks of low-resolution maps: would a single water molecule of about 1.5 Å hydrogen-to-hydrogen distance really generate a distinct peak in a 3.5 Å electron-density map? While Fig. 6 ▶ does allow a coarse estimate of how may waters can be expected to be built at a certain resolution, the ultimate criteria are reasonable electron density (satisfying the need for evidence) and physico-chemical plausibility (satisfying the need for compliance with well established prior expectations).

3.1.5. Partially occupied water molecules  

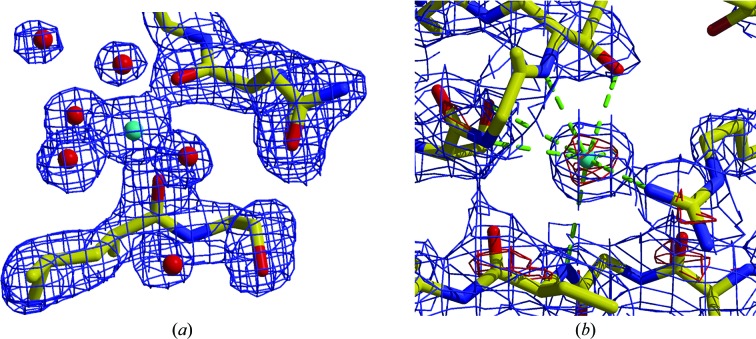
When water molecules refine to high B factors, which is simply an indication that the refinement program wants less scattering contribution at the proposed water location, it can be justified to assign a partial occupancy of the water atom. Doing so will reduce the B factor and, given the (at medium resolution) almost identical effect of decreasing the occupancy or increasing the B factor, it will have little effect on the global R values. Justification therefore must come from necessity, such as distinct water densities that are perhaps too close to another one, indicating reduced occupancies (with their sum ≤1.0) or water positions that are correlated with alternate side-chain confirmations. Respective occupancy groups can be defined in the refinement programs and, if appropriate, their sum constrained to 1.0. Fig. 7 ▶ exemplifies a relatively simple instance of such a situation.

Figure 7.

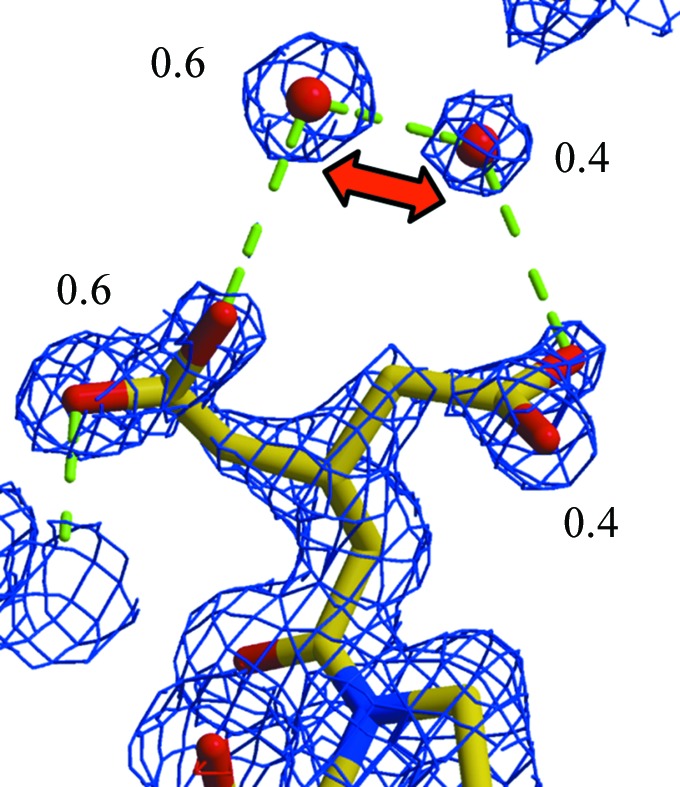
Example of alternate conformations correlated with partial water occupancy. The Glu side chain split at C^β assumes two approximately 60/40% occupied alternate conformations. The two water atoms are too close to be present at the same time, and their occupancies should be related to those of the associated side chains. The sum of the occupancies of the two groups must be constrained to 1.0. 2mF _o − DF _c electron density is contoured at the 1σ level. This figure was modified from Rupp (2009 ▶).

3.1.6. Low B-factor ‘water’ molecules  

Low B-factor waters that deviate significantly below the B factors of neighbouring protein atoms or even approach the hard-coded lower limits for B factors (often set at 1–5 Ų in refinement programs) are indicative of the incorrect assignment of metal cations, or of anions such as Cl⁻, as water molecules (see Echols, Morshed et al., 2014 ▶ and Fig. 8 ▶). In many cases, the coordination geometry and bond distances for ions (see §3.2), a review of the crystallization-cocktail components (see §3.2) and/or anomalous difference map peaks will allow a sensible explanation.

Figure 8.

Identification of elemental ions. (a) The central atom has electron density comparable to water but displays the typical octahedral coordination of a metal ion. The coordination distances of 2.0–2.2 Å are compatible with Mg²⁺ ions isoelectronic with the surrounding waters. PDB entry 1gkb (Kantardjieff et al., 2002 ▶). (b) An originally modelled water atom with improbably low B factors can be identified as Cl⁻ by electron-density peak height, coordination distances (3.1–3.7 Å) and its preference to bind to backbone N atoms and positively charged residues. PDB entry 1c8u (Li et al., 2000 ▶). 2mF _o − DF _c electron density is contoured at the 1σ level (blue) and the 5σ level (red). The figures are modified from Rupp (2009 ▶).

3.2. Elemental ions  

Elemental ions such as cations of various natively present metals or those originating from the crystallization cocktail are almost always present in a crystal structure. Similarly, but less frequently, anions from cryo-salts can be present in crystal structures. In the case of quick ion soaks for anomalous phasing, the presence of ordered (but not necessarily fully occupied) ions and their anomalous scattering contributions is a desired outcome. Distinction between ions such as NH₄ ⁺, Na⁺ and Mg²⁺, all of which are practically isoelectronic with water (ten electrons), cannot in general be achieved on the basis of electron density or atomic displacement parameters alone. Discrimination of such isoelectronic ion sites is possible via interpretation of their bonding and coordination environments. For heavier ions, the electron density will be correspondingly higher than for water molecules, and erroneously modelled waters in place of heavier ions therefore refine to implausibly low B factors. In cases where anomalous data have been collected, anomalous difference density maps (see Strahs & Kraut, 1968 ▶; Mueller-Dieckmann et al., 2007 ▶; Read & McCoy, 2011 ▶) can be a powerful means to provide experimental evidence for localized metals. A corresponding X-ray absorption/fluorescence edge scan can identify the ion, and to some degree its local environment (Frankaer et al., 2014 ▶).

Coordination distances and geometries for most elemental ions have been tabulated, for example by Harding (2004 ▶, 2006 ▶) and Hsin et al. (2008 ▶). These parameters provide a basis for validation servers such as CheckMyMetal (Zheng et al., 2014 ▶). Coordinate-based a posteriori validation is necessarily not as powerful as combined validation/identification that includes electron density and anomalous difference peak analysis (Echols, Morshed et al., 2014 ▶), which is a convincing reason to record, keep and deposit unmerged anomalous diffraction data if at all possible.

3.3. Small-molecule ligands  

Binding sites have, by their nature, evolved to attract ligand moieties. While specifics assure that the correct substrate is processed in vivo, even remotely similar molecular moieties (i.e. anything from expression host cellular contents to purification buffers to crystallization-cocktail components) can be forced into a binding site by a high enough concentration (and can even partly replace or entirely compete out the desired ligand). The potential of weak binders being forced into active sites given sufficient concentration can be used to advantage in fragment-based drug-lead discovery (Burley, 2004 ▶; Hajduk & Greer, 2007 ▶), but it can lead to unexpected ligands such as buffers in the binding site (Gokulan et al., 2005 ▶) or to the misinterpretation of spurious density, which may then be modelled with a desired but fictional ligand (Rupp, 2010 ▶; Pozharski et al., 2013 ▶; Dauter et al., 2014 ▶).

The presence of large solvent channels in macromolecular crystals allows the soaking of small molecules (mostly ligands, inhibitors, therapeutic drug leads, cofactors or nonhydro­lysable substrates) into pre-formed crystals. Should soaking not be possible, co-crystallization remains an option. The techniques are well established (Danley, 2006 ▶; Hassell et al., 2007 ▶). Prerequisites for successful soaking experiments are solvent channels that are large enough to allow the respective ligand to diffuse into the crystal. The specific diffusion rate and the on-rate for ligand binding determine the time that it will take to achieve binding of the ligand, which ranges from several minutes to many hours. In small single-ion soaking, as is used for SAD phasing (Nagem et al., 2001 ▶, 2003 ▶), partial occupancies are acceptable, which can be achieved in as little as 60–300 s.

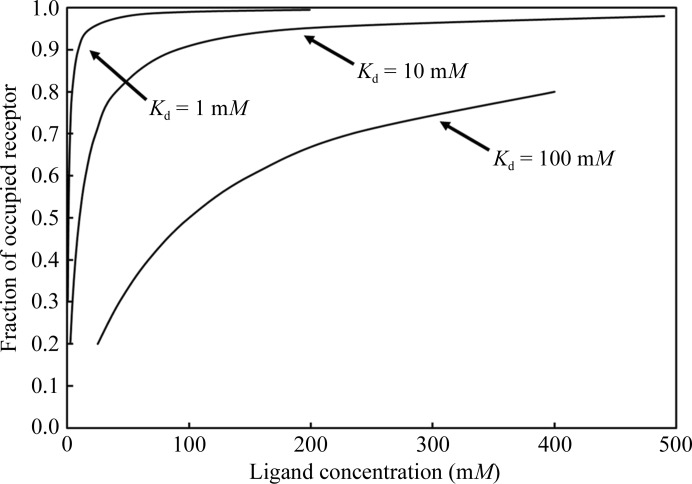
The occupancy of a ligand site is a direct function of the binding affinity and ligand concentration; it can be derived (Danley, 2006 ▶) from the definition of the dissociation constant K _d and is illustrated in Fig. 9 ▶. If a ligand does not have a high binding affinity, it will not have full occupancy at low concentrations and therefore even less of its already low relative scattering mass will contribute to the (uninformative for ligand-validation purposes) global refinement residuals (Pozharski et al., 2013 ▶; Weichenberger et al., 2013 ▶). Similarly, any contributions to the corresponding ligand electron density will be reduced in proportion to the ligand occupancy. However, high occupancy can still be reached even at a low K _d by sufficiently high concentrations, effectively forcing the ligand (or a crystallization-cocktail component) into a binding site (Fig. 9 ▶).

Figure 9.

Fraction of occupied receptor sites plotted against ligand equilibrium concentration for three different binding constants. While in the millimolar and lower K _d range small concentrations of ligand suffice to achieve reasonable binding-site occupancy (between 70 and 90%), quite impractical concentrations of ligand in the crystallization drop are required for poor binders. On the other hand, given a sufficiently high concentration, even weakly binding (and non-native) ligands can be forced into a binding site. Figure from Pozharski et al. (2013 ▶) calculated as derived in Danley (2006 ▶) and Rupp (2009 ▶).

3.3.1. Experimental evidence  

The proposition that a ligand in a complex structure is located in a specific position, exhibiting a unique conformation (i.e. present in a specific pose) is a very strong and powerful statement. Correspondingly, clear experimental evidence to back this strong claim is necessary. Clear positive OMIT difference electron density (Bhat, 1988 ▶) has been proposed as a minimum requirement to justify ligand placement based on experimental crystallographic data (Kleywegt, 2007 ▶; Pozharski et al., 2013 ▶; Wlodawer et al., 2013 ▶; Dauter et al., 2014 ▶). The OMIT difference density should be generated without the ligand molecule ever being placed into the elsewhere almost finished model. Otherwise, the ligand phase bias must be removed at a minimum by means such as re-refinement of the model after slight coordinate perturbation (Reddy et al., 2003 ▶) or more rigorous methods (Hodel et al., 1992 ▶; Adams et al., 1997 ▶; Brünger et al., 1997 ▶; Terwilliger et al., 2008 ▶).

In general, very high ligand B factors and low partial ligand occupancies, particularly when combined, do not provide sufficient scattering contributions, and convincing positive difference density can seldom be reconstructed. The absence of supporting ligand electron density is typically revealed by high real-space R (RSR) values and low real-space correlation coefficients (RSCCs), as calculated by various refinement packages or with separate tools such as Coot (Emsley et al., 2010 ▶), EDSTATS (Tickle, 2012 ▶) or OVERLAPMAP (Winn et al., 2011 ▶). The EDS electron-density server (Kleywegt et al., 2004 ▶) provides electron-density analysis for most published PDB entries. Note that EDS density is not ligand-omit density, and is therefore biased towards the presence of a ligand rather than its absence. The latest PDB validation reports provide another, combined measure of ligand fit, the local ligand density fit (LLDF; http://wwpdb.org/ValidationPDFNotes.html) comparing the RSR of the ligand to the mean and standard deviation of the RSR for protein atoms within 5 Å. In cases where ligands contain heavier atoms, anomalous difference data can provide clues towards their identification and evidence for their presence (Strahs & Kraut, 1968 ▶; Thorn & Sheldrick, 2011 ▶). While obvious for ligands containing phosphate moieties or heavy-metal ions, an educational example of the identification of the S atom in HEPES buffer by means of anomalous difference Fourier density is provided in a publicly available tutorial collection (Faust et al., 2008 ▶).

3.3.2. Plausibility  

The weaker the scattering contributions and therefore the reconstructed electron density, the more one must rely on stereochemical restraints and the nature of the chemical environment of the proposed ligand. Poor restraint files often lead to implausible ligand geometries upon refinement (Kleywegt, 2007 ▶), and databases have been created to allow the comparison of ligand geometry with known (but not necessarily correct) PDB ligand entries (Kleywegt & Harris, 2007 ▶). PDB Ligand Expo (http://ligand-expo.rcsb.org) provides a collection of tools to access ligand structures already present in PDB files. Multiple tools exist to generate ligand restraint files based on high-resolution small-molecule crystallographic data and/or quantum-mechanical optimization (Schüttelkopf & van Aalten, 2004 ▶; Moriarty et al., 2009 ▶; Smart et al., 2011 ▶; Lebedev et al., 2012 ▶), with additional resources tabulated in Deller & Rupp (2015 ▶).

In addition to the ligand geometry, the pose of the ligand needs to be plausible and to allow corresponding contacts with the macromolecule which can be examined in model-building tools such as Coot (Emsley et al., 2010 ▶). Graphical display programs such as LIGPLOT (Laskowski & Swindells, 2011 ▶) enable visualization of the local environment of a ligand in its binding site.

3.3.3. R _free set selection and model bias  

Protein–ligand complex structures are often determined by molecular replace­ment from already known protein structure models. In the case of an isomorphous structure, simple rigid-body refinement followed by rebuilding and individual coordinate refinement may suffice. The same reflections as selected for the R _free set of the original data set should be kept for proper cross-validation (Brünger, 1997 ▶). In addition, if another isomorphous structure with a ligand has been used as a starting model for re-refinement, spurious density resembling the original ligand can be reproduced as a result of model phase bias. Although modern maximum-likelihood methods are relatively robust against model bias, this possibility should be kept in mind. An initial round of simulated-annealing molecular-dynamics refinement (Adams et al., 1997 ▶) or small coordinate perturbations (Perrakis et al., 1997 ▶; Reddy et al., 2003 ▶), always with the ligand omitted (Bhat, 1988 ▶), can be used to minimize bias issues if these are suspected. If data from an isomorphous and ligand-free apo crystal are also available, F _obs(ligand) − F _obs(apo) difference maps revealing unbiased ligand density can be generated (Stryer et al., 1963 ▶).

3.4. Automated ligand-building tools  

Ligand identification in itself is often the very goal of a crystal structure determination, initiating time- and resource-expensive steps down the line. The application and limitations of X-ray crystal structure models for structure-guided lead discovery (Blundell et al., 2002 ▶; Tickle et al., 2004 ▶), fragment screening (Burley, 2004 ▶; Hartshorn et al., 2005 ▶; Fischer & Hubbard, 2009 ▶) and drug design (Goodwill, 2001 ▶) have been reviewed elsewhere (Davis et al., 2008 ▶). As in the case of ordered solvent modelling outlined in §3.1.2, automated programs for ligand placement have been developed and implemented in most crystallo­graphic structure-determination (Oldfield, 2001 ▶; Zwart et al., 2004 ▶; Wlodek et al., 2006 ▶; Terwilliger et al., 2006 ▶, 2007 ▶; Binkowski et al., 2010 ▶; Klei et al., 2014 ▶; Echols, Moriarty et al., 2014 ▶; Carolan & Lamzin, 2014 ▶) and validation (Kleywegt, 2007 ▶; Kleywegt & Harris, 2007 ▶; Smart et al., 2011 ▶; Pozharski et al., 2013 ▶; Weichenberger et al., 2013 ▶) packages.

While it may seem counterintuitive, ligand identification and placement are conceptually simpler tasks than ‘single-atom’ (such as water and metal ion) model building. Differentiating a single peak in a Fourier map from noise and interpreting it in terms of an atom type are difficult tasks, because at typical macromolecular resolutions Fourier maps alone do not convey the information necessary to identify the chemical element type. Consequently, most water-building tools are limited and use only very basic information, such as difference map peak height, density shape (sphericity) and position with respect to neighbouring peaks or already placed atoms. Identification of non-water single-atom ions can use more heuristics, such as preferred chemical environments and characteristic peaks in anomalous difference maps, when available.

Ligands containing more than one atom carry extra information, which is crucial to uniquely and unambiguously identify and place them: the shape. However, a combination of imperfections may transform the shape of the ligand density quite significantly and make its interpretation a challenging task. Contributing factors are (i) pathologies related to crystal quality (anisotropy, twinning etc.), (ii) widely varying diffraction data quality (resolution, completeness, experimental errors etc.) and (iii) the intrinsic nature of ligands being flexible and dynamic. As a result model quality can vary widely, and corresponding validation against evidence and prior expectations as outlined in §§3.3.1 and 3.3.2 is necessary.

3.5. Crystallization-cocktail components  

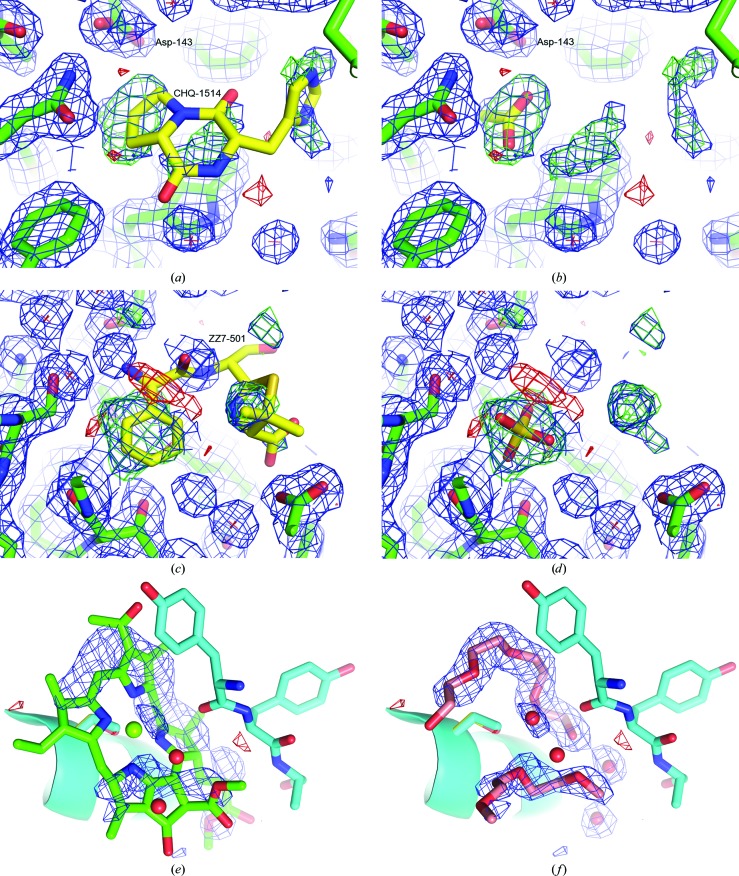
The vast majority of proteins only crystallize in the presence of a highly concentrated precipitant cocktail which, together with components from high concentrations of cryoprotecting agents, can provide a source of unintended ligands. Consequently, components of the crystallization cocktail are often the source of some electron density visible in a known binding site. Occasionally, specific interactions are formed in these sites, and the identity of the unexpected ligand is clearly revealed (Gokulan et al., 2005 ▶). In the case of unexpected ligands that are disordered and appear in or near the predicted target binding sites, it may be rather tempting to place the ligand of interest in an arbitrary or even a plausible pose into such uninterpretable density (Fig. 10 ▶). The poor fit may then be explained by invoking the possibility that the ligand binds in multiple conformations. For instance, in PDB entry 3qd1/4i8e (Pyburn et al., 2011 ▶) a disaccharide was positioned into difference density that can readily be identified as originating from a HEPES molecule (Muller, 2013 ▶). In a recent analysis (Pozharski et al., 2013 ▶; Weichenberger et al., 2013 ▶) it was found that a significant fraction of problematic ligands belong to the class of misinterpreted crystallization-cocktail components. Using critical analysis and examining plausible sources of not clearly interpretable electron density can almost always prevent the biased misinterpretation of such electron density as the desired ligands.

Figure 10.

Ligands placed into density of mother-liquor components. In the structure of Bacillus cereus chitinase (PDB entry 3n1a; Hsieh et al., 2010 ▶), the cyclo-(l-His-l-Pro) molecule (CHQ-1514, chain A) is placed into low-level electron density that is difficult to interpret (a) and which may be plausibly interpreted as an acetate molecule present in the crystallization cocktail at 200 mM, supported by a newly formed hydrogen bond between Asp-143 and the suggested acetate (b). In the structure of penicillin-binding protein 4 from Staphylococcus aureus (PDB entry 3hun; Navratna et al., 2010 ▶) the phenyl moiety of the ampicillin (ZZ7-501, chain B) is placed in a region of the electron density that based on difference density analysis could be better interpreted as a sulfate ion (c). The re-refined model that includes sulfate ion is shown in (d). (e) The original, obsoleted and distorted bacteriochlorophyll model at the eighth binding site in the FMO protein from Pelodictyon phaeum (PDB entry 3oeg); (f) depicts the same region of the corrected PDB entry 3vdi (Tronrud & Allen, 2012 ▶) modelled with more plausible PEG fragments and water molecules. Electron-density maps in (a), (b), (c) and (d) are 2.0 Å resolution mF _o − DF _c OMIT difference maps contoured at ±3σ (green/red) and 2mF _o − DF _c REFMAC maximum-likelihood OMIT maps contoured at 1σ (blue). The maps shown in (e) and (f) are positive difference density OMIT mF _o − DF _c maps (3σ level, blue) after BUSTER-TNT refinement following rebuilding of the structure with phenix.autobuild without any ligand included. (a), (b), (c) and (d) are modified from Pozharski et al. (2013 ▶); (e) and (f) were kindly supplied by Dale Tronrud, Department of Biochemistry and Biophysics, Oregon State University, USA.

4. Summary of solvent constituents and tools for their treatment  

The solvent is an integral and also often an intricate part of almost any macromolecular crystal structure. Its disordered bulk components as well as its ordered constituents of varying nature need to be accounted for in modelling and refinement. The improvement of bulk-solvent description from a fundamental perspective is largely driven by methods development. In bulk-solvent refinement, users have relatively little choice beyond solvent-model selection and not much opportunity for the introduction of bias or specific model errors, with the caveat that suboptimal masking can introduce density artefacts. Modelling of distinct solvent electron density requires thoughtful interpretation, and using appropriate tools for (automated) building and validation can greatly improve the quality of structure models. A summary of frequently encountered tasks and current tools for solvent treatment, modelling and validation are provided in Table 2 ▶.

Table 2. Summary of common tasks and current tools for bulk-solvent treatment and modelling and validation of ordered solvent constituents.

Task	Program	Reference
Solvent-content estimate	MATTPROB	Matthews (1968 ▶), Kantardjieff Rupp (2003 ▶), Weichenberger Rupp (2014 ▶)
	MATTHEWS_COEF	Matthews (1968 ▶), Winn et al. (2011 ▶)
	Phaser	McCoy et al. (2007 ▶)
	BUSTER	Bricogne et al. (2010 ▶)
	PHENIX	Adams et al. (2010 ▶)
Solvent masking, density modification	SOLOMON	Abrahams Leslie (1996 ▶)
	AutoSHARP	Vonrhein et al. (2007 ▶)
	DM, DMMULTI	Kostrewa (1997 ▶), Cowtan (2010 ▶)
	SHELXE	Sheldrick (2010 ▶)
	PHENIX	Adams et al. (2010 ▶)
Water building, sorting	arp_waters	Perrakis et al. (1997 ▶), Winn et al. (2011 ▶)
	WATNCS	Winn et al. (2011 ▶)
	WATERTIDY	Winn et al. (2011 ▶)
	SHELXWAT	Sheldrick (2008 ▶)
	CNS	Brunger (2007 ▶)
	Coot	Emsley et al. (2010 ▶)
	PHENIX	Adams et al. (2010 ▶)
Metal identification, validation	CheckMyMetal	Zheng et al. (2014 ▶)
	PHENIX	Echols, Morshed et al. (2014 ▶)
	Anomalous difference maps	Read McCoy (2011 ▶), Mueller-Dieckmann et al. (2007 ▶)
	ANODE	Thorn Sheldrick (2011 ▶)
	Distance-geometry table	Hsin et al. (2008 ▶), Harding Hsin (2014 ▶)
Ligand restraint files	PDB Ligand Expo	Feng et al. (2004 ▶)
	PRODRG	Schttelkopf van Aalten (2004 ▶)
	Grade	Smart et al. (2011 ▶)
	JLigand	Lebedev et al. (2012 ▶)
	PHENIX eLBOW	Moriarty et al. (2009 ▶)
	Coot	Debreczeni Emsley (2012 ▶)
	Mogul	Bruno et al. (2004 ▶)
Ligand building	Coot	Emsley et al. (2010 ▶)
	ARP/wARP ligand	Carolan Lamzin (2014 ▶)
	PHENIX	Echols, Moriarty et al. (2014 ▶)
Ligand validation	EDS	Kleywegt et al. (2004 ▶)
	EDSTATS	Tickle (2012 ▶)
	OVERLAPMAP	Winn et al. (2011 ▶)
	HIC-Up	Kleywegt (2007 ▶)
	ValLigURL	Kleywegt Harris (2007 ▶)
	VHELIBS	Cereto-Massagu et al. (2013 ▶)
	Twilight	Weichenberger et al. (2013 ▶), Pozharski et al. (2013 ▶)
	LIGPLOT	Laskowski Swindells (2011 ▶)
	Coot	Emsley et al. (2010 ▶), Debreczeni Emsley (2012 ▶)
	BUSTER	Smart et al. (2011 ▶)
	PDB (RSR Z score, LLDF)	Read et al. (2011 ▶), http://wwpdb.org/ValidationPDFNotes.html