Abstract
Background
Multiple types of neural signals are available for controlling assistive devices through brain–computer interfaces (BCIs). Intracortically recorded spiking neural signals are attractive for BCIs because they can in principle provide greater fidelity of encoded information compared to electrocorticographic (ECoG) signals and electroencephalograms (EEGs). Recent reports show that the information content of these spiking neural signals can be reliably extracted simply by causally band-pass filtering the recorded extracellular voltage signals and then applying a spike detection threshold, without relying on “sorting” action potentials.
New method
We show that replacing the causal filter with an equivalent non-causal filter increases the information content extracted from the extracellular spiking signal and improves decoding of intended movement direction. This method can be used for real-time BCI applications by using a 4 ms lag between recording and filtering neural signals.
Results
Across 18 sessions from two people with tetraplegia enrolled in the BrainGate2 pilot clinical trial, we found that threshold crossing events extracted using this non-causal filtering method were significantly more informative of each participant’s intended cursor kinematics compared to threshold crossing events derived from causally filtered signals. This new method decreased the mean angular error between the intended and decoded cursor direction by 9.7° for participant S3, who was implanted 5.4 years prior to this study, and by 3.5° for participant T2, who was implanted 3 months prior to this study.
Keywords: Spike sorting, Neural decoding, Threshold crossing, Non-causal filter, Brain–computer interface, Microelectrode array
1. Introduction
By translating a person’s neural activity into control of a computer cursor, robotic arm or other assistive device, brain–computer interfaces (BCIs) can potentially restore communication or functional independence to individuals with severe movement disabilities. Based upon years of basic research, one BCI approach has been to decode intended arm or hand movements from the activity of populations of single neurons recorded with an electrode array implanted in motor cortical areas. In previous work, the activity of different neurons recorded on a single electrode has typically been discriminated by specifying a template capturing the unique waveform shape of each neuron’s recorded action potentials (“spike sorting”) (Serruya et al., 2002; Taylor et al., 2002); however, this process is time consuming and yields inconsistent results even among experts (Wood et al., 2004). The requirement to sort spikes becomes more imposing with increasing numbers of implanted recording electrodes and presents a barrier to independent use of spike-based BCIs by individuals with paralysis. Further, detecting the action potentials of individual neurons can be difficult if their waveforms cannot be isolated from background electrical activity or from those of other nearby neurons. This problem can be further exacerbated if the amplitude of the recorded action potentials decreases over months and years post-implant (Chestek et al., 2011) or when signal amplitudes are nonstationary on the timescale of minutes and hours (Perge et al., 2013). Although many algorithms have been developed to try to isolate waveforms of single neurons and track their amplitudes despite signal nonstationarities (Franke et al., 2010; Calabrese and Paninski, 2011), none have been completely satisfactory (Wild et al., 2012) and it remains problematic for BCIs to rely on the precise shape of extracellularly recorded waveforms (Wood et al., 2004; Quiroga, 2012).
Recently, several non-human primate studies have suggested that spike sorting might not be critical for estimating intended movements in some motor BCI applications (Fraser et al., 2009; Chestek et al., 2011). In those ensemble decoding studies, the rate at which the filtered neural electrical signals crossed a pre-determined voltage threshold (the “threshold crossing” rate) provided nearly an equivalent amount of information about the discrete direction of intended movements as did the spike rates of isolated, single neurons, irrespective of whether the threshold crossings detected on each electrode came from one or multiple neurons. Threshold crossing rates have successfully been used for real-time neural control in monkeys (Chestek et al., 2011) and people (Hochberg et al., 2012) even years after microelectrode array implantation when signal amplitudes were small and sorting single-neuron action potential waveforms would have been challenging.
Given the potential benefits of employing threshold crossings for the control of BCIs, we sought to evaluate neural signal processing improvements to the standard threshold crossing method. To extract action potentials, the common waveform sorting and threshold crossing methods pre-filter raw neural signals with a causal filter (i.e. the output of the filter only depends on the past and present inputs). However, a recent offline study of extracellular recordings demonstrated that signal distortions arising from such causal filtering results in smaller spike amplitudes and can cause noise artifacts to resemble action potentials, thereby reducing the accuracy of spike detection (Quian Quiroga, 2009). In contrast, non-causal signal filtering was found to improve action potential discrimination (Quian Quiroga, 2009). Given this evidence, we investigated whether non-causal (zero-phase) signal processing could enhance spike detection and improve kinematic estimation for two BCI users with paralysis in the BrainGate2 pilot clinical trial. We show here that a non-causal filter applied to each neural signal channel prior to threshold detection extracts spiking activity that is more strongly correlated with intended movements when compared to the causal bandpass filter. Furthermore, non-causal filtering resulted in better population decoding of instantaneous intended 2-D cursor kinematics than the traditional causal filtering method. Notably, this improvement was observed for both large and small amplitude neural signals recorded from microelectrode arrays implanted 3 months and 5.4 years prior to those BrainGate2 sessions (for participants T2 and S3, respectively). We developed a method for real-time computation of the non-causal filter that was subsequently used by trial participants with paralysis for closed-loop neural control of a computer cursor in a Radial-8 assessment task (Jarosiewicz et al., 2013) and command of a robotic arm to perform 3D reach and grasp movements (Hochberg et al., 2012).
2. Materials and methods
Permission for these studies was granted by the US Food and Drug Administration (Investigational Device Exemption) and the Partners Healthcare/Massachusetts General Hospital Institutional Review Board. The two participants in this study, S3 and T2, were enrolled in a pilot clinical trial of the BrainGate Neural Interface System (additional information about the clinical trial is available at http://www.clinicaltrials.gov/ct2/show/NCT00912041).
2.1. Participants
Data from two participants enrolled in the BrainGate2 clinical trial4 were included in this study. Their conditions have been previously described in detail (Hochberg et al., 2012). Participant S3 is female, 58 years old at the time of this study, with tetraplegia and anarthria (inability to speak) resulting from a pontine stroke that occurred 9 years prior to array implantation. She retains eye movement, some head movement and facial expression, and breathes spontaneously. She has bilateral upper extremity flexor spasms that occur sporadically with many intended body movements. On November 30, 2005, a 96-channel intracortical silicon microelectrode array (produced by Cyberkinetics Neurotechnology Systems, Inc., and now by its successor, Blackrock Microsystems, Salt Lake City, UT) was implanted in the arm area of her motor cortex. The data reported here come from 12 sessions recorded between S3 trial days (i.e., days after implantation) 1904–1975. These were the last 12 sessions in which S3 controlled a computer cursor before successfully completing her enrollment in the BrainGate2 clinical trial.
The second study participant, referred to as T2, is male, ambidextrous, and was 65-years old at the time of this study. He has tetraplegia and anarthria resulting from a brainstem stroke that occurred 5 years prior to array implantation. With the exception of unreliable and trace right wrist and index finger extension (but not flexion), he is without voluntary movement at and below C5. He was implanted with the Blackrock array in the arm area of his left motor cortex on June 9, 2011. The data reported here come from 6 sessions between T2’s trial days 67 and 82. These were the first 6 sessions of T2’s enrollment in the BrainGate2 clinical trials in which he controlled a computer cursor.
2.2. Setup
During each session, the participant was seated in a wheelchair, slightly reclined from vertical, and faced a 17 inch flat panel monitor (34 cm × 27 cm, 1280 × 1024 pixels) centered slightly above eye level at a distance of approximately 56 cm. A technician used aseptic technique to connect a 96-channel recording cable between a percutaneous pedestal connector on the participant’s head and the signal amplifier and then used commercial software (Cerebus Central, Blackrock Microsystems, Salt Lake City, UT) to view neural signal waveforms. The analog neural signals for each electrode (or “channel”) were broadband-filtered (0.3 Hz–7.5 kHz) by the Black-rock Microsystems amplifier but were otherwise unprocessed prior to being digitized at 30 kHz and stored for offline analysis.
2.3. Behavioral task
For each of the sessions analyzed here, the participants’ goal was to move a computer cursor to targets appearing one by one on a computer monitor by modulating his or her neural activity. Each session began with one or more “open-loop” decoder calibration “blocks” lasting 2–4 min (Simeral et al., 2011; Hochberg et al., 2012) in which the participant watched the cursor make preprogrammed straight-line movements from a starting target at the center of the screen to one of four peripheral targets positioned on the cardinal axes, and then back to the center target. Out-and-back movements occurred to each of the four peripheral targets (without replacement) before the block continued with a new randomized order for the four peripheral targets. While watching these movements, the participants were instructed to imagine that they were moving their dominant hand to control the cursor, allowing us to map neural activity to desired movements. Each trial (i.e. each movement from the center target to a peripheral target, or from a peripheral target back to center) lasted 2.5–5 s, and each block consisted of 12–24 trials. For S3, there was a single open-loop block in each session. For T2, there were six open-loop blocks in each session. For this study, we analyzed data from only the initial open-loop block in each session.
2.4. Computing causal and non-causal threshold crossing rates
In offline analysis of each open-loop data block, the raw neural signals from each electrode (channel) were converted into threshold crossing rates in three steps. (1) The raw signal was filtered with a 4th order Butterworth bandpass filter with corners at 250 Hz and 5000 Hz, either causally (using the Matlab command filter) or non-causally (using the Matlab command filtfilt), otherwise known as zero-phase filtering. (2) A spike detection threshold was calculated as −4.5 times the standard deviation of the filtered signal (−4.5 × RMS). To prevent comparatively large spike amplitudes or noise bursts from artificially inflating the estimate of the standard deviation, we estimated the RMS using the median of the filtered signal (x) (Quiroga et al., 2004):
In participant S3, the mean RMS values were 6.02 ± 4.92 μV for the causal and 5.64 ± 4.02 μV for the non-causal filter, and in participant T2, the mean RMS values were 9.17 ± 1.10 μV for the causal, and 8.71 ± 1.01 μV for the non-causal filter. (3) A threshold crossing rate was computed as the number of times that the filtered signal crossed below this threshold in 100 ms frames, corresponding to the frame size of the cursor kinematics in this study.
The non-causal filter applied in this study yields a zero-phase response by passing over the data twice – once forward and once in reverse. One result is that the effective order of the non-causal filter is double that of the corresponding causal (single-pass) filter (effectively an 8th order filter in this study). To test and control for the effects of filter order on the results, we repeated our analyses for 4th, 6th, and 8th order causal filters. We also assessed sensitivity of the results to the choice of filter passband.
2.5. Comparing spike amplitudes from causal and non-causal filters
We quantified the effect of different filtering methods on the amplitudes of (putative) spiking events by comparing voltage minima of corresponding causal and non-causal threshold crossing events on all qualifying channels (see Section 2.7) from all analyzed sessions. Because causal and non-causal filters have different phase responses, the local minima of causally and non-causally filtered signals can occur at slightly different times. Thus, for this analysis, we identified corresponding spiking events by searching for the minimum value of the non-causally filtered signal that occurred within 200 μs of each valid threshold crossing event in the causally filtered signal. If that non-causal minimum value was also below the −4.5 × RMS threshold, this spiking event was included in the analysis. To prevent channels with high firing rates from contributing disproportionately to the analysis of spike amplitudes, only the first 100 spiking events per channel per session were included in the analysis.
2.6. Calculating directional tuning of threshold crossing rates
Threshold crossing rates were computed for each channel (recording electrode) irrespective of whether the spiking activity was derived from one or more single cortical neurons or multiple indiscriminable neurons (sometimes referred to as “multiunit hash”). Nonetheless, a channel’s threshold crossing rates commonly vary with the direction of intended movements and can be fit to a directional tuning model with preferred direction and modulation depth as is common in traditional single unit tuning analysis. For each channel, a directional tuning model was derived for threshold crossings that occurred in the interval 0.5–2 s after onset of the pre-programmed cursor movements as participants imagined making target-directed hand movements. Specifically, we modeled the threshold crossing rate on channel i at time t, zi(t) as the dot product between the unit’s preferred direction, Hi, and the participant’s intended movement direction, d(t) (a unit vector assumed to point directly from the center of the cursor toward the center of the target),
where bi and εi are the baseline spike rate and Gaussian noise for that unit, respectively. The constant c shifts the neural data relative to the intended movement direction to account for the participants’ reaction time between cursor updates on the computer screen and neural responses. This constant was set to 200 ms (Jarosiewicz et al., 2013), as and was chosen because it produced the largest directional modulation in off-line analyses (data not shown). Given bi, Hi and εi for each channel, we compared three metrics between causally filtered and non-causally filtered threshold crossing rates. The first was the baseline rate, bi, which, given uniform sampling of intended directions, corresponds to the channel’s mean rate. The second was the modulation depth, ||Hi||, the vector norm of Hi This value is equal to the expected increase in the threshold crossing rate above baseline when the participant imagined moving in the preferred direction of that channel. The third metric was the normalized modulation depth (Hochberg et al., 2012; Jarosiewicz et al., 2013), defined as ||Hi||/std(εi) which is equal to the reciprocal of the coefficient of variation. We note that the normalized modulation depth (NMD) metric is related to the signal-to-noise ratio (SNR) as
assuming uniform sampling of cursor directions.
2.7. Channel selection
In this study, the voltage signal (or noise) recorded on each individual microelectrode is referred to as a “channel”. For each analyzed session, channels that had very high noise levels and/or no apparent modulation with movement direction were excluded from analysis. Specifically, we excluded a channel from the analysis if its baseline threshold crossing rate was above 100 Hz for both the causal and non-causal filtering methods, or if its normalized modulation depth was below 0.1 for both the causal and non-causal filtering methods. Also, because accurately estimating a channel’s movement-related modulation depth is diminished for very low rates, we only included channels in the analysis for which the baseline rate was above 0.25 Hz for at least one of the causal or non-causal filtering methods.
2.8. Decoding intended movement
To determine whether differences between causal and non-causal filtering resulted in meaningful differences in movement-related information content of the recorded neural ensemble, we decoded each participant’s neural signals to estimate intended movement direction from the open-loop blocks using a Kalman filter (Wu et al., 2006; Kim et al., 2011). To prevent overfitting, we included in the Kalman filter only channels that satisfied the criteria described above. Additionally, if more than 30 channels satisfied these criteria, we included only the top 30 channels with the greatest normalized modulation depths. The Kalman filter is constructed using four estimated parameters: H, Q, A and W. The first parameter is the matrix of preferred directions of each channel, H, as defined above. The second is the error covariance matrix in reconstructing the threshold crossing rates:
The third matrix is a “state model” which defines the linear relation between the intended movement directions at consecutive time points, d(t) = Ad(t − 1), and the fourth set is the error in this state model:
These last two values were set to constant values (A = 0.965I and W = 0.03I where I is the identity matrix) as in previous studies (Hochberg et al., 2012; Jarosiewicz et al., 2013) to provide a balance between responsiveness and smoothness of decoded cursor movement. For all time steps of each trial in each session, we decoded the intended movement using a Kalman filter that was calibrated using all other trials in that session. This resulted in a decoded (estimated) movement direction for every 100 ms time step in each trial’s 1.5 s analysis window (see above).
Decoding accuracy was calculated for each condition (e.g., causal filter or non-causal filter) on each day as the mean dot product between the decoded movement direction and the actual direction of the pre-programmed cursor movement (dot products were averaged across all time steps, with 60–200 s per session). For example, a decoding accuracy of 1 would be consistent with perfect direction estimation at all time points, a value of 0 would indicate a mean 90° error, and a value of −1 would result if direction estimates at every time point were exactly opposite to the actual cursor movement.
2.9. Decoding movement intention from the LFP power
Several previous studies have shown that movement intention can be reliably estimated from the power within specific frequency bands of the local field potential (Stark and Abeles, 2007; Bansal et al., 2012; Flint et al., 2012; Perge et al., 2014). We wanted to compare the decoding accuracy of these methods based on LFP power to our decoding approach based on causal and non-causal threshold crossings. Thus, we calculated the LFP power in the spiking frequency band based on the method proposed by Stark and Abeles (2007). For each channel, we causally filtered neural signals using a 3rd order Butterworth filter with a pass band between 300 and 6000 Hz. We then capped values above or below 2 standard deviations from the mean, and calculated the RMS of the filtered and capped signals for each 100 ms frame. We then decoded intended movements using these RMS values in the same manner as we did for threshold crossings.
2.10. Statistical tests
We found that the metrics comparing causal and non-causal filtering (waveform amplitudes, baseline rates, normalized modulation depths and decoding accuracy) were not normally distributed. Thus, we applied non-parametric Wilcoxon rank tests for statistical analysis. All reported p-values are 2-tailed.
3. Results and discussion
A principle goal of this study was to determine whether filtering spiking neural signals non-causally produced threshold crossing rates that were more informative about the participant’s intended movements than filtering signals using the standard causal method. We also examined whether non-causal filtering resulted in significantly more accurate multi-channel decoding of intended hand kinematics for BCI users with paralysis. Finally, we tested the robustness of the non-causal threshold crossing method to conditions of large and small amplitude neural signals, different filter characteristics, and choice of spike detection threshold.
We analyzed data from two BrainGate2 trial participants, T2 and S3, each implanted with a 96-microelectrode array (Black-rock Microsystems, Salt Lake City, UT) 3 months and 5.4 years prior to this study, respectively. Across 18 evaluated recording sessions (1728 total channels recorded), 642 channels satisfied analysis criteria (T2: 348 channels, 6 sessions; S3: 326 channels, 12 sessions).
3.1. Impact of non-causal filtering on spike amplitudes in recorded intracortical neural signals
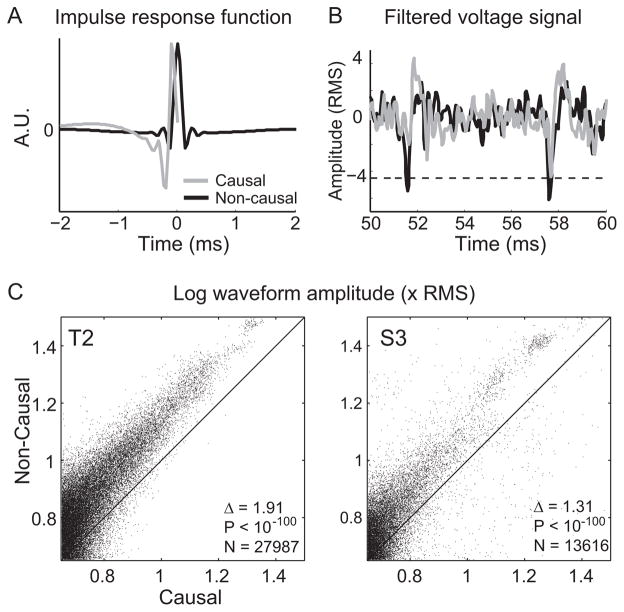
For each channel, spiking activity was extracted from the open-loop blocks in each session using causal and non-causal 4th order Butterworth filters with a frequency range between 250 Hz and 5000 Hz. Given the different impulse responses of these two filters (Fig. 1A), the Matched Filter Theorem (Turin, 1976) leads to the hypothesis that convolving the neural signal with the filter better matched to recorded action potentials should produce larger amplitude spikes. As a representative example, Fig. 1B shows 10 ms of a neural signal from S3 in which two putative spiking events occurred. The causally filtered signal (gray line) crossed the threshold for only one of these events, whereas the spiking amplitudes were larger for the non-causally filtered signal bringing both events across threshold.
Fig. 1.
Causal and non-causal filtering. (A) The shape of the causal filter (gray curve) and the non-causal filter (black curve). Both filters are 4th order bandpass (250–5000 Hz) Butterworth filters. The non-causal filter is more localized than the causal filter (i.e. the amplitude of the non-causal filter is significantly different from zero for a much shorter duration than the causal filter), and might be better matched to the shape of a typical action potential. (B) Example of 10 ms of continuous signal filtered causally (gray curve) and non-causally (black curve). The non-causal filter accentuates the amplitude of putative spiking events, allowing them to cross threshold (dashed black line, set at −4.5 × RMS). (C) Scatter plot of the amplitude (relative to the RMS of the signal) of threshold crossing events using the causal filter (x-axis) versus using the non-causal filter (y-axis) for participant T2. Each dot represents one spiking event. A maximum of 100 spiking events were used per channel per session. Amplitudes are plotted on a log10 scale. Δ gives the mean pairwise difference between the amplitude of causal and non-causal spiking events. Fewer than 0.3% of points fall outside the plot window. (D) Same as (C), except for participant S3. Fewer than 0.1% of points fall outside the plot window.
To test whether the amplitude of (putative) spiking events was systematically larger for non-causally than causally filtered signals, we compared the corresponding amplitudes of all spiking events on all channels (Fig. 1C and D). We found that amplitudes (measured relative to the RMS of the signal) of the non-causally filtered spiking events were consistently and significantly larger than the corresponding causally filtered spiking events (T2 causal amplitude = 6.21 ± 2.26 × RMS, non-causal amplitude = 8.13 ± 3.65 × RMS, p < 10−100; S3 causal amplitude = 6.42 ± 3.86 × RMS, non-causal amplitude = 7.72 ± 5.46 × RMS, p < 10−100, mean ± standard deviation).
Although our non-causal filter has double the order of the corresponding causal filter, filter order and pass band limits did not contribute meaningfully to the different effects of the causal and non-causal filters (see Section 3.3). Thus, in these data, non-causal filtering accentuated spike amplitudes in recorded intracortical neural signals.
3.2. Impact of non-causal filtering on estimation of intended movement kinematics
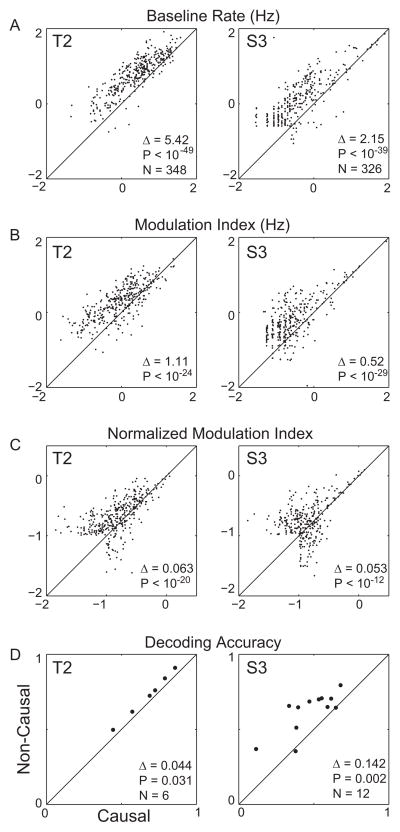
To determine whether non-causal filtering affected the information content of the threshold crossing events, we first obtained the rates of threshold crossing events from both the causally and non-causally filtered signal in 100 ms frames. We then mapped the relationship between neural activity and the participant’s intended movements by fit-ting a directional tuning model to the threshold crossing rates computed using causal and non-causal filtering (see Section 2). Finally, we compared three different parameters extracted from this regression (Fig. 2): the baseline rate, the modulation depth (amplitude of the cosine fit), and the normalized modulation depth (modulation depth divided by the standard deviation of the residuals). Baseline threshold crossing rates varied between participants and filtering method (Fig. 2A; T2 causal baseline = 5.03 ± 6.00 Hz, non-causal baseline = 10.45 ± 10.90 Hz; S3 causal baseline = 2.19 ± 7.93 Hz, non-causal baseline = 4.34 ± 10.09 Hz). In both T2 and S3, as expected from the larger amplitudes of non-causally filtered spikes, baseline threshold crossing rates were greater using non-causally filtered signals than using causally-filtered signals (T2: mean pairwise difference (Δ) = 5.42 ± 7.66 Hz, p < 10−49; S3: Δ = 2.15 ± 6.76 Hz, p < 10−41). The bands that appear for S3 are the results of a few low-firing channels that produced only a handful of spikes in the analysis windows.
Fig. 2.
Comparing tuning metrics between causal and non-causal threshold crossing events. (A) Scatter plot of baseline threshold crossing rates using the causal filter method (x-axis) versus baseline threshold crossing rates using the non-causal filter method, plotted on a log scale, for T2 (left column) and S3 (right column). Δ gives the mean difference in the baseline rates between the causal and non-causal filter methods. (B) Same as (A), except plotting modulation depth. (C) Same as (A), except plotting normalized modulation depths. (D) The decoding accuracy (defined as the mean dot product between the decoded and actual cursor direction) for the six T2 sessions (left column) and the twelve S3 sessions (right column).
Importantly, in both participants, directional tuning modulation depths were also larger for non-causally filtered threshold crossings than for causally filtered threshold crossings (Fig. 2B; T2 causal modulation depth = 2.04 ± 3.27 Hz, non-causal modulation depth = 3.15 ± 3.41 Hz, Δ = 1.11 ± 2.40 Hz, p < 10−24; S3 causal modulation depth = 1.07 ± 5.16 Hz, non-causal modulation depth = 1.59 ± 4.87 Hz, Δ = 0.52 ± 1.15 Hz, p < 10−29). That is, the additional spikes captured with non-causal filtering added information about intended movement direction and yielded more robust directional tuning. In principle, it was possible that the non-causal method captured more “noise” as well (threshold crossings in the neural signal that were not related to movement). Thus, we computed the normalized modulation depth, which is equal to the amplitude of the cosine fit over the noise of the fit. We found that the normalized modulation depths on all channels were greater for threshold crossing events extracted from non-causally filtered signals than from causally filtered signals (Fig. 2C; T2 causal normalized modulation depth = 0.20 ± 0.17, non-causal normalized modulation depth = 0.27 ± 0.18, Δ = 0.06 ± 0.12, p < 10−20; S3 causal normalized modulation depth = 0.17 ± 0.16, non-causal normalized modulation depth = 0.22 ± 0.19, Δ = 0.05 ± 0.12, p < 10−12). Hence, the added directional information did not come at the expense of added non-directional noise.
The foregoing analyses demonstrated better detection of movement information on single channels using a non-causal filter. To test whether non-causal filtering also resulted in improved instantaneous estimation of intended kinematics from ensembles of recorded channels, we compared offline population decoding accuracy using the two filtering methods. Consistent with the single channel results, we found that decoding accuracy was higher when extracting threshold crossings using the non-causal filter compared to the causal filter (Fig. 2D, T2 causal decoding accuracy = 0.68 ± 0.15, non-causal decoding accuracy = 0.72 ± 0.15, Δ = 0.04 ± 0.01, p = 0.031; S3 causal decoding accuracy = 0.48 ± 0.16, non-causal decoding accuracy = 0.62 ± 0.14, Δ = 0.14 ± 0.10, p = 0.002). Switching from a causal to a non-causal filter decreased the mean angular error in the decoded direction from 47.2° to 43.6° for T2, and from 61.6° to 51.9° for S3.
3.3. Robustness of non-causal filtering improvements to design choices
To make sure that the conclusions regarding causal vs. non-causal filters generalized with variations in filter order and frequency bands, we repeated the analyses using various filter orders and pass bands that are reasonable for spike detection. The decoding accuracy using the non-causal filtering method was significantly higher than the causal method for all five pass bands for S3, and three out of five pass bands for T2 (Table 1). The two pass bands that were not significantly different for T2 also showed a trend toward higher decoding accuracy using the causal method (both p-values were less than 0.1). The filter order was of particular interest because non-causal filtering effectively filters the signal twice (once in the forward and once in the reverse direction in time) leading to sharper roll-off in power at the cut-off frequencies than with causal filtering. Thus, to control for this sharper roll-off, we repeated the above analyses using a 6th and a 8th order causal filter and compared decoding performance to that achieved with the 4th-order non-causal filter. Changing the causal filter’s order did not affect our results (Table 1). Thus, the sharper roll-off of the non-causal filter does not account for its advantage over causal filtering.
Table 1.
Change in decoding accuracy (defined as the mean dot-product between the decoded and actual cursor direction) between causal and non-causal threshold crossing events using different filter passbands and orders). Note that the p-value for T2 is consistently p = 0.031 because the statistical test used (Wilcoxon signed-rank) is a rank-based test, and all non-causal decoding accuracies were greater than their causal counterparts.
| Passband (Hz) | Filter order
|
S3
|
T2
|
|||||
|---|---|---|---|---|---|---|---|---|
| Non-causal | Causal | Non-causal | Causal | p-Value | Non-causal | Causal | p-Value | |
| 250–5000 | 4th | 4th | 0.617 | 0.475 | 0.002 | 0.724 | 0.680 | 0.031 |
| 500–5000 | 4th | 4th | 0.586 | 0.365 | 0.001 | 0.710 | 0.662 | 0.031 |
| 250–6000 | 4th | 4th | 0.585 | 0.484 | 0.010 | 0.718 | 0.686 | 0.094 |
| 300–6000 | 4th | 4th | 0.588 | 0.438 | 0.001 | 0.715 | 0.680 | 0.031 |
| 250–7500 | 4th | 4th | 0.549 | 0.420 | 0.003 | 0.710 | 0.681 | 0.063 |
| 250–5000 | 4th | 6th | 0.617 | 0.437 | 0.003 | 0.724 | 0.651 | 0.031 |
| 250–5000 | 4th | 8th | 0.617 | 0.356 | 0.001 | 0.724 | 0.639 | 0.031 |
Interestingly, decoding accuracy actually decreased when using a 6th and a 8th order causal filter. This is likely because higher order filters tend to produce more ringing, which create oscillatory artifacts in the filtered signal. Thus, choosing the right order for a Butterworth filter is a trade-off between achieving a sufficiently sharp frequency response and a tolerable amount of ringing.
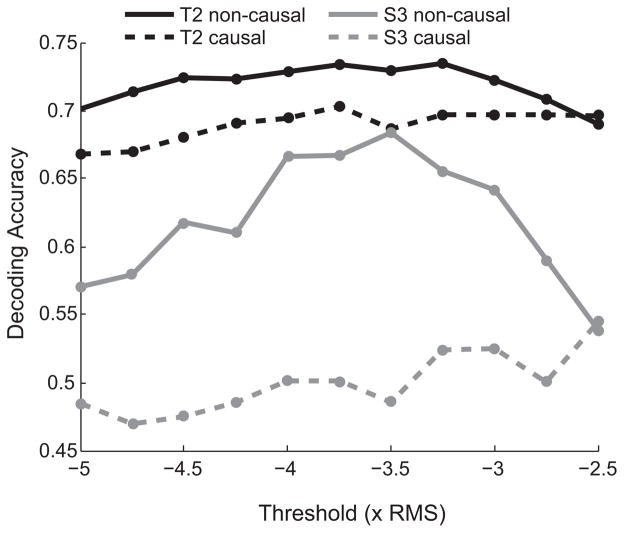
An important question was whether the choice of detection threshold was critical to the improvements observed for the non-causal threshold detection process. As in our previous work (Hochberg et al., 2012) and that of others (Chestek et al., 2011), this study applied a detection threshold of −4.5 × RMS (−4.5 times the filtered signal’s root mean square value) computed separately for each channel. To test whether these findings generalize for different thresholds, we repeated our analyses for a range of threshold values. For each, we re-extracted new threshold crossing rates for every channel in every session using the new threshold for both causal and non-causal methods, generated new Kalman decoders and computed the decoding accuracy metric for each method for each session (see Section 2), and computed the mean decoding accuracy across sessions for each method for each participant. As shown in Table 2, the decoding accuracy was significantly greater using the non-causal filter method for 8 out of 9 thresholds between −3 and −5 × RMS for S3, and for 7 out of 9 thresholds between −3 and −5 × RMS for T2, indicating that the decoding quality improvements generalized well across thresholds. Although non-causal threshold crossings yielded better decoding performance across the range of thresholds tested here, the choice of threshold was not irrelevant as absolute decoding accuracy for both methods was somewhat dependent on choice of spike detection threshold (Fig. 3). For S3, non-causal decoding performance peaked at −3.5 × RMS. Similarly, non-causal decoding performance for T2 peaked between −3.25 and −3.75 × RMS, with a shallower performance function than in S3. The significance of the different relationship between decoding performance and threshold value for S3 and T2 remains a topic for further investigation but may be related in part to the difference in the raw recorded signal amplitudes in this study (discussed next).
Table 2.
Decoding accuracy for causal and non-causal threshold crossing events using different thresholds.
| Threshold (×RMS) | S3
|
T2
|
||||
|---|---|---|---|---|---|---|
| Non-causal | Causal | p-Value | Non-causal | Causal | p-Value | |
| −2.5 | 0.538 | 0.545 | 0.969 | 0.690 | 0.696 | 0.563 |
| −2.75 | 0.591 | 0.500 | 0.052 | 0.709 | 0.697 | 0.219 |
| −3.0 | 0.641 | 0.525 | 0.002 | 0.723 | 0.697 | 0.031 |
| −3.25 | 0.656 | 0.524 | 0.001 | 0.735 | 0.697 | 0.063 |
| −3.5 | 0.684 | 0.486 | 0.001 | 0.730 | 0.686 | 0.031 |
| −3.75 | 0.667 | 0.502 | 0.001 | 0.733 | 0.703 | 0.031 |
| −4.0 | 0.666 | 0.501 | 0.001 | 0.729 | 0.694 | 0.031 |
| −4.25 | 0.610 | 0.485 | 0.002 | 0.724 | 0.691 | 0.063 |
| −4.5 | 0.617 | 0.475 | 0.002 | 0.724 | 0.680 | 0.031 |
| −4.75 | 0.580 | 0.469 | 0.063 | 0.713 | 0.669 | 0.031 |
| −5.0 | 0.570 | 0.485 | 0.027 | 0.701 | 0.668 | 0.031 |
Fig. 3.
Decoding accuracy as a function of threshold. The mean decoding accuracy is shown for thresholds ranging from −5 to −2.5 × RMS for T2 (black curves) and S3 (gray curves) obtained with the causal filter method (dashed lines) and the non-causal filter method (solid lines).
3.4. Robustness of non-causal filtering effects to amplitude of recorded neural signals
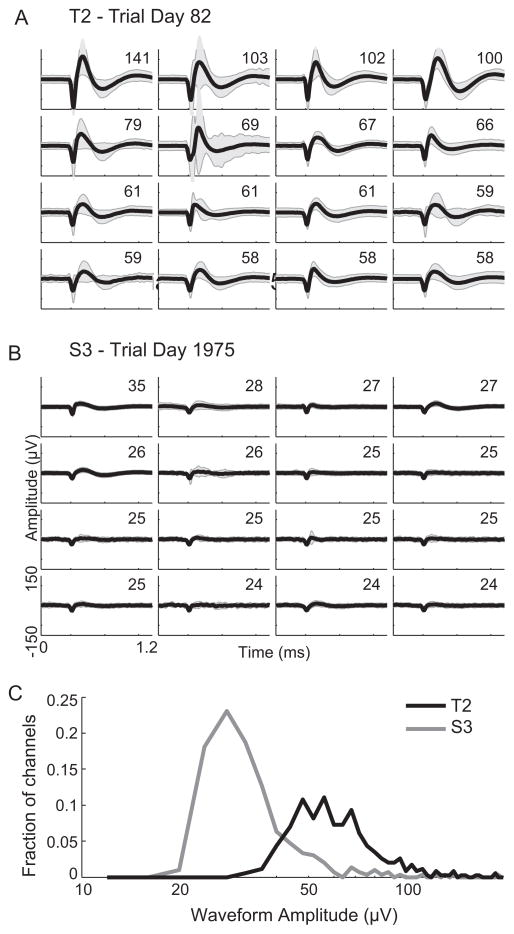
Even though the neural signals selected for this study from participant S3 were markedly smaller in amplitude than those from T2, the benefits observed with non-causal filtering were consistent across both participants. Fig. 4A and B shows threshold crossing waveforms from the 16 non-causally filtered channels with the highest amplitude from an example session for each participant. Across all sessions analyzed in this study, the mean amplitude of the non-causal threshold crossings recorded from the T2 array were greater than the S3 array (T2 amplitude = 67.4 ± 24.4 μV, S3 amplitude = 36.8 ± 18.4 μV; p < 10−100). This difference in signal amplitudes was systematic across channels and days (Fig. 4C). Because S3’s microelectrode recording array had been implanted 5.4 years at the time of this study compared to 3 months for T2’s array, the difference in amplitudes observed here may reflect a gradual decline in signal amplitudes that has been observed over months and years in chronically implanted microelectrodes in monkeys (Chestek et al., 2011; Barrese et al., 2013) and people (Simeral et al., 2011). Our results using neural data from both a newer and an older array demonstrate that non-causal filtering can extract more informative signals under both high-and low-amplitude action potential conditions. While maintaining long-term signal quality across years is expected to improve through engineering more reliable electrode arrays (Gilja et al., 2011), our results suggest that non-causal threshold crossing could provide one small but effective means for mitigating the effects of declining amplitudes should they occur.
Fig. 4.
Threshold crossing waveforms from the two participants. (A) The average waveform of threshold crossing events (black curve) ± 2 times the waveform standard deviation (gray shaded area) for the 16 channels with the largest waveform amplitudes (defined as the absolute value of the minimum of the mean waveform) recorded from T2 on trial day 82. The numbers in the top-right of each give the waveform amplitude (in μV), defined as the absolute value of the minimum of the mean waveform. (B) Same as (A), showing the waveforms recorded from S3 on trial day 1975. (C) Histogram of the mean waveform amplitudes (defined as the minimum of the mean of all waveforms that crossed the −4.5 times RMS threshold) for all 348 T2 channels (black curve) and all 326 S3 channels (gray curve). Waveforms for this plot were obtained from the non-causal filter method.
3.5. Comparison to non-spike detection methods
Several previous studies have suggested that movement intentions can be accurately decoded using the power in specific frequency bands of the local field potential (Stark and Abeles, 2007; Bansal et al., 2011; Flint et al., 2012; Perge et al., 2014). Thus, we wanted to compare the decoding accuracy extracted from causal and non-causal threshold crossings to these other methods that use LFP power. To do so, we calculated the power in the spiking band of the LFP using the method proposed by Stark and Abeles (2007) (see Section 2), and then used this spike power as the feature to decode movement intention. Decoding using the power in the spiking band of the LFP yielded slightly but significantly higher accuracy than traditional (causal) threshold crossings (p = 0.048, data from both participants combined), but lower accuracy than non-casual threshold crossings (p < 10−3) when using the appropriate threshold (−3.5 × RMS). The latter difference was also significant when comparing each participant’s results separately (T2: p = 0.031; S3: p = 0.002).
3.6. Real-time computation of non-causal threshold crossing
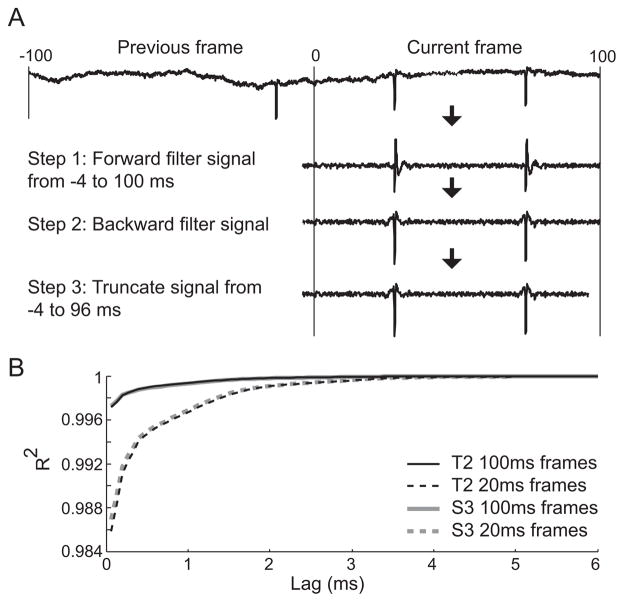
The analysis presented above was calculated offline using previously recorded data. For real-time BCI applications (Hochberg et al., 2012), neural signals were non-causally filtered before computing the number of threshold crossings that occurred in 100 ms (S3) or 20 ms (T2) frames of data. Below, we first present the rationale and the method we used to non-causally filter signals, for which we implemented a 4 ms delay between the threshold crossing rates and cursor kinematics (Fig. 5A). We then present analysis confirming that this 4 ms delay is sufficient to accurately non-causally filter signals in (relative) real-time (Fig. 5B).
Fig. 5.
Near real-time non-causal filtering. (A) Neural signals were non-causally filtered in (near) real time in three steps. We show the case using 100 ms frames, but different frame durations can be used. First, the signal from 4 ms before the frame to the end of the frame is forward filtered. Second, this signal is backwards filtered. Third, the last 4 ms of the signal is truncated to eliminate edge effects on the forward end. This method allows for non-causal threshold crossing to be computed with a 4 ms delay relative to the kinematics (B) Analysis showing that 4 ms is the minimum delay needed to accurately non-causally filter neural signals in near real time. The Pearson correlation coefficient was calculated between non-causally filtered signals using all time points and signals filtered using the method described in (A) in which the delay was varied. Results are shown for T2 (black) and S3 (gray curves) using either 100 ms (solid) or 20 ms (dashed curves) frames.
The output of a (causally) filtered signal depends on the previous values of the signal. The number of relevant previous values is dependent on the type and pass band of the filter. If the previous signal values are unknown, then the filtered signal will differ from the case in which the previous values were known. This discrepancy is referred to as “edge effects”. When causally filtering a signal, edge effects occur only at the start of the recording and are therefore not an issue. However, non-causally filtering a signal involves first filtering the signal forward in time, and then filtering the signal backwards in time. When filtering a signal backwards in time, edge effects occur when the future signal values are unknown. Thus, care must be taken to avoid edge effects when non-causally filtering the signal in real time.
To avoid edge effects, we implemented real-time non-causal filtering in the following three steps (Fig. 5A). We only show the case for 100 ms frames, but the analogous case holds for frames of any length. For the current 100 ms frame, we forward filter the signal from 4 ms before the start of the frame until the end, producing a 104 ms long causally filtered signal. Because we always know the previous signal values (with the exception of the first recorded frame), this filtered signal is free of edge effects. Second, we backwards filter this signal, producing a 104 ms long non-causally filtered signal. However, because we do not know the future signal values, edge effects will be present at the “future” end. Thus, in step three we remove the last 4 ms of this frame, leaving a 100 ms long non-causally filtered signal that is (virtually) free of edge effects. The only cost is that this signal is delayed 4 ms from true real time.
To confirm that a 4 ms delay was sufficient to remove most of the edge effects, we first non-causally filtered neural signals using all time points, which served as a ground truth. We then non-causally filtered the same signals, using the method described above, using either 20 or 100 ms frames and variable delays (ranging between 1/15 and 6 ms). We then calculated the Pearson correlation coefficient between these two signals (Fig. 5B) using the first session of S3 data and the first session of T2 data (results from other sessions were very similar). For both 20 and 100 ms frames, correlations values saturated (R2 > 0.999) for delays of 4 ms and greater. Thus, a 4 ms delay is sufficient to remove edge effects when implementing a non-causally filter for use in real-time decoding.
4. Summary and future work
We have shown that the non-causal filter is superior to the causal filter for extracting useful spiking signals in both low-amplitude and high-amplitude signal regimes, irrespective of the frequency range of the filter used for isolating spikes, the filter order, and the threshold value. Non-causally filtering intracortical neural signals produced threshold crossing events with larger amplitudes and threshold crossing rates that were better modulated and more informative of the participant’s intended movements. This resulted in significantly better instant-by-instant estimation of intended movement kinematics, relative to the standard causal filtering approach, for individuals with paralysis using the BrainGate2 BCI. This was true for neural signals recorded from an intracortical electrode array 3 months after implant with relatively high-amplitude spike signals, and for an array 5.4 years after implant with relatively low amplitude spike signals. By extracting more information from low-amplitude signals, non-causal filtering could help to extend the life of useful spike-recording capabilities of intracortical electrode arrays. We developed a real-time implementation of the non-causal threshold crossing method, which we used in two recent BCI studies to allow BrainGate2 participants to neurally control 2D computer cursor movements (Jarosiewicz et al., 2013) and 3D robotic arm reach and grasp movements (Hochberg et al., 2012) as long as 5 years after array implantation.
The detection and decoding of threshold crossing events is a method that, by definition, does not attempt to discriminate the recorded activity of single neurons. Our offline analyses (here, and other work not published), as well as previous studies (Santhanam et al., 2004; Fraser et al., 2009; Chestek et al., 2011), suggest that adequate kinematic decoding can be achieved using threshold crossing rates instead of sorted-unit activity. Though it is recognized that well sorted single units from an electrode may encode different information pertinent to the decoding of intended movement, our work is further motivated by challenges of unit sorting (time required to sort units, inconsistent results among experts, and the difficulty of maintaining single unit sorting over extended periods of time). In this report we have not attempted to compare decoding performance using threshold crossings to decoding populations of sorted single units. However, the Matching Filter theorem would predict that the non-causal filter evaluated in this study would be advantageous in waveform-sorting single-unit procedures as well. Our hypothesis that non-causal filtering would extract more informative signals was based on the fact that the shape of the Butterworth bandpass non-causal filter was better matched to the shape of the canonical action potential than its causal counterpart. However, we make no claim that this filter shape is optimal in extracting informative spiking signals. Given that the spectral density of the noise, and that the shapes of any action potentials, will vary between channels, there is likely no one optimal filter.
Thus, instead of choosing a single filter shape, one could convolve neural signals with a family of wavelets (Kim and Kim, 2003; Quiroga et al., 2004; Nenadic and Burdick, 2005). Different wavelets will be sensitive to different spectral features, and if a family of wavelets is correctly chosen, then action potentials of any shape would match well with at least one of more wavelets. This approach is much more computationally intensive than the method proposed in this study. However, with the steady increase in computational power, convolving many channels of high-sample rate signals with wavelets in real time is a realistic possibility.
Alternatively, other signal processing methods could be used if the amplitude of spiking events were too low for isolating action potentials from single neurons. For example, the total signal power within the spiking frequency band could potentially be more informative of movement than a count of isolated action potentials (Stark and Abeles, 2007). Furthermore, it might be useful to combine non-causal filtering with spike power and other such methods to help extract useful signals for BCI control in low-amplitude signal regimes.
In summary, a non-causal filter, as opposed to a causal filter, can extract threshold crossing events that are more informative of the participant’s intended movements. Switching to a non-causal filter is simple to implement, and leads to improvements in decoding that are consistent across a range of signal-to-noise ratios, pass bands, and filter orders.
HIGHLIGHTS.
Non-causally filtering intracortical neural signals improves BCI decoding.
Compared to causal filtering, it increases spike amplitudes and improves tuning.
These improvements hold across different filter properties and signal qualities.
Non-causal filtering can be implemented for real-time decoding with a 4 ms lag.
Acknowledgments
We thank participants S3 and T2 for their dedication to this research. We thank David Rosler, Laurie Barefoot, Katherine Centrella, and the caregiver staff at the Boston Home for their contributions to this research. The contents do not necessarily represent the views of the Department of Veterans Affairs or the United States Government. This work was supported by NIH: NIDCD (R01DC009899) and NICHD-NCMRR (N01HD53403, N01HD10018); Rehabilitation Research and Development Service, Office of Research and Development, Department of Veterans Affairs (Merit Review Awards B6453R and A6779I); Doris Duke Charitable Foundation, Craig H. Neilsen Foundation, MGH-Deane Institute for Integrated Research on Atrial Fibrillation and Stroke, and the Katie Samson Foundation. The pilot clinical trial into which participant S3 was recruited was sponsored in part by Cyberkinetics Neurotechnology Systems (CKI). The BrainGate clinical trial is directed by Massachusetts General Hospital.
Footnotes
A production error resulted in this article appearing in the wrong issue. This article is reprinted here for the reader’s convenience and for the continuity of the special issue. For citation purpose, please use the original publication details “Journal of Neuroscience Methods” 236 (2014) 58–67.
Caution: Investigational Device. Limited by Federal Law to Investigational Use.
Conflict of interest
The authors declare no conflict of interest.
References
- Bansal AK, Truccolo W, Vargas-Irwin CE, Donoghue JP. Decoding 3D reach and grasp from hybrid signals in motor and premotor cortices: spikes, multiunit activity, and local field potentials. J Neurophysiol. 2012;107(March 5):1337–55. doi: 10.1152/jn.00781.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bansal AK, Vargas-Irwin CE, Truccolo W, Donoghue JP. Relationships among low-frequency local field potentials, spiking activity, and three-dimensional reach and grasp kinematics in primary motor and ventral premotor cortices. J Neurophysiol. 2011;105(April 4):1603–19. doi: 10.1152/jn.00532.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrese JC, Rao N, Paroo K, Triebwasser C, Vargas-Irwin C, Franquemont L, et al. Failure mode analysis of silicon-based intracortical microelectrode arrays in non-human primates. J Neural Eng. 2013;10(December 6):066014. doi: 10.1088/1741-2560/10/6/066014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabrese A, Paninski L. Kalman filter mixture model for spike sorting of non-stationary data. J Neurosci Methods. 2011;196(March 1):159–69. doi: 10.1016/j.jneumeth.2010.12.002. [DOI] [PubMed] [Google Scholar]
- Chestek CA, Gilja V, Nuyujukian P, Foster JD, Fan JM, Kaufman MT, et al. Long-term stability of neural prosthetic control signals from silicon cortical arrays in rhesus macaque motor cortex. J Neural Eng. 2011;8(August 4):045005. doi: 10.1088/1741-2560/8/4/045005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint RD, Lindberg EW, Jordan LR, Miller LE, Slutzky MW. Accurate decoding of reaching movements from field potentials in the absence of spikes. J Neural Eng. 2012;9(August 4):046006. doi: 10.1088/1741-2560/9/4/046006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke F, Natora M, Boucsein C, Munk MHJ, Obermayer K. An online spike detection and spike classification algorithm capable of instantaneous resolution of overlapping spikes. J Comput Neurosci. 2010;29(August 1/2):127–48. doi: 10.1007/s10827-009-0163-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser GW, Chase SM, Whitford A, Schwartz AB. Control of a brain–computer interface without spike sorting. J Neural Eng. 2009;6(October 5):055004. doi: 10.1088/1741-2560/6/5/055004. [DOI] [PubMed] [Google Scholar]
- Gilja V, Chestek CA, Diester I, Henderson JM, Deisseroth K, Shenoy KV. Challenges and opportunities for next-generation intracortically based neural prostheses. IEEE Trans Biomed Eng. 2011;58(July 7):1891–9. doi: 10.1109/TBME.2011.2107553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochberg LR, Bacher D, Jarosiewicz B, Masse NY, Simeral JD, Vogel J, et al. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature. 2012;485(7398):372–5. doi: 10.1038/nature11076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarosiewicz B, Masse NY, Bacher D, Cash SS, Eskandar E, Friehs G, et al. Advantages of closed-loop calibration in intracortical brain–computer interfaces for people with tetraplegia. J Neural Eng. 2013;10(August 4):046012. doi: 10.1088/1741-2560/10/4/046012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim KH, Kim SJ. A wavelet-based method for action potential detection from extracellular neural signal recording with low signal-to-noise ratio. IEEE Trans Biomed Eng. 2003;50(August 8):999–1011. doi: 10.1109/TBME.2003.814523. [DOI] [PubMed] [Google Scholar]
- Kim S-P, Simeral JD, Hochberg LR, Donoghue JP, Friehs GM, Black MJ. Point-and-click cursor control with an intracortical neural interface system by humans with tetraplegia. IEEE Trans Neural Syst Rehabil Eng. 2011;19(April 2):193–203. doi: 10.1109/TNSRE.2011.2107750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nenadic Z, Burdick JW. Spike detection using the continuous wavelet transform. IEEE Trans Biomed Eng IEEE. 2005;52(January 1):74–87. doi: 10.1109/TBME.2004.839800. [DOI] [PubMed] [Google Scholar]
- Perge JA, Homer ML, Malik WQ, Cash S, Eskandar E, Friehs G, et al. Intra-day signal instabilities affect decoding performance in an intracortical neural interface system. J Neural Eng. 2013;10(June 3):036004. doi: 10.1088/1741-2560/10/3/036004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perge JA, Zhang S, Malik WQ, Homer ML, Cash S, Friehs G, et al. Reliability of directional information in unsorted spikes and local field potentials recorded in human motor cortex. J Neural Eng. 2014;11(June 4):046007. doi: 10.1088/1741-2560/11/4/046007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quian Quiroga R. What is the real shape of extracellular spikes? J Neurosci Methods. 2009;177(February 1):194–8. doi: 10.1016/j.jneumeth.2008.09.033. [DOI] [PubMed] [Google Scholar]
- Quiroga RQ. Spike sorting. Curr Biol. 2012;22(January 2):R45–6. doi: 10.1016/j.cub.2011.11.005. [DOI] [PubMed] [Google Scholar]
- Quiroga RQ, Nadasdy Z, Ben-Shaul Y. Unsupervised spike detection and sorting with wavelets and superparamagnetic clustering. Neural Comput. 2004;16(August 8):1661–87. doi: 10.1162/089976604774201631. [DOI] [PubMed] [Google Scholar]
- Santhanam G, Sahani M, Ryu S, Shenoy K. An extensible infrastructure for fully automated spike sorting during online experiments. Conf Proc IEEE Eng Med Biol Soc. 2004;6(January):4380–4. doi: 10.1109/IEMBS.2004.1404219. [DOI] [PubMed] [Google Scholar]
- Serruya MD, Hatsopoulos NG, Paninski L, Fellows MR, Donoghue JP. Instant neural control of a movement signal. Nature. 2002;416(March 6877):141–2. doi: 10.1038/416141a. [DOI] [PubMed] [Google Scholar]
- Simeral JD, Kim S-P, Black MJ, Donoghue JP, Hochberg LR. Neural control of cursor trajectory and click by a human with tetraplegia 1000 days after implant of an intracortical microelectrode array. J Neural Eng. 2011;8(April 2):025027. doi: 10.1088/1741-2560/8/2/025027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark E, Abeles M. Predicting movement from multiunit activity. J Neurosci. 2007;27(August 31):8387–94. doi: 10.1523/JNEUROSCI.1321-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor DM, Helms Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002;80(296):1829–32. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- Turin GL. An introduction to digitial matched filters. Proc IEEE. 1976;64(7):1092–112. [Google Scholar]
- Wild J, Prekopcsak Z, Sieger T, Novak D, Jech R. Performance comparison of extracellular spike sorting algorithms for single-channel recordings. J Neurosci Methods. 2012;203(January 2):369–76. doi: 10.1016/j.jneumeth.2011.10.013. [DOI] [PubMed] [Google Scholar]
- Wood F, Black MJ, Vargas-Irwin C, Fellows M, Donoghue JP. On the variability of manual spike sorting. IEEE Trans Biomed Eng. 2004;51(June 6):912–8. doi: 10.1109/TBME.2004.826677. [DOI] [PubMed] [Google Scholar]
- Wu W, Gao Y, Bienenstock E, Donoghue JP, Black MJ. Bayesian population decoding of motor cortical activity using a Kalman filter. Neural Comput. 2006;18(January 1):80–118. doi: 10.1162/089976606774841585. [DOI] [PubMed] [Google Scholar]