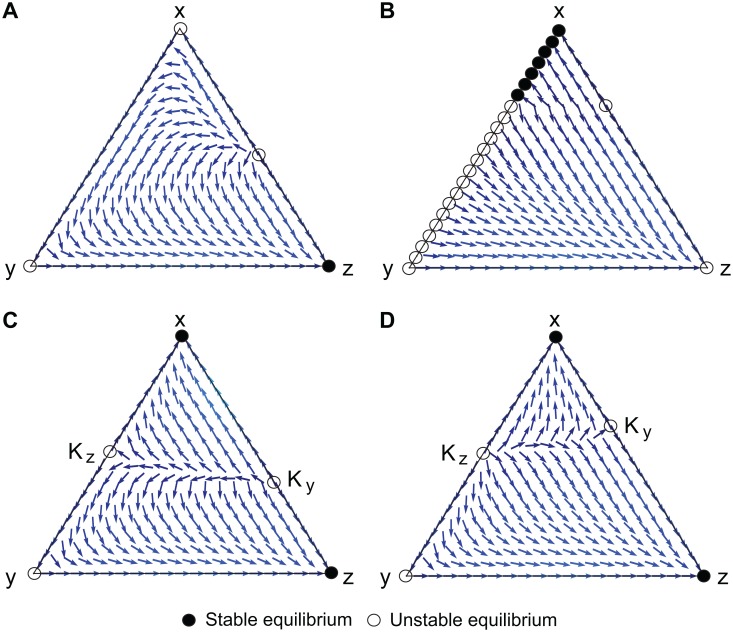
Fig 3. Replicator dynamics analysis of representative S-MIGs on 2-dimensional simplex.

The triangle represents the state space, Δ = {(x, y, z)*** : x, y, z ≥ 0, x+y+z = 1}, where x, y, and z are respectively the frequencies of the cooperative incentive-providers, cooperative incentive-non-providers, and non-cooperative incentive-non-providers. $(\mu ,\delta )=(3,\frac{1}{2})$. (A) PR+R, (B) PP, (C) PB+RB(Full), and (D) RB. The abbreviations are defined in Table 1. In (A), (x, y, z) = (1, 0, 0) is unstable, so cooperation is never achieved regardless of the values of (μ, δ). In (B), the whole line z = 0 consists of fixed points, and thus, neutral drift is possible. In (C) and (D), (x, y, z) = (1, 0, 0) is a locally asymptotically stable point depending on the values of (μ, δ), and thus, a cooperative regime can emerge. In (C), the unstable equilibrium in the internal part on z = 0, K _z, is a saddle, and that on y = 0, K _y, is a source. In (D), K _z is a source, while K _y is a saddle.