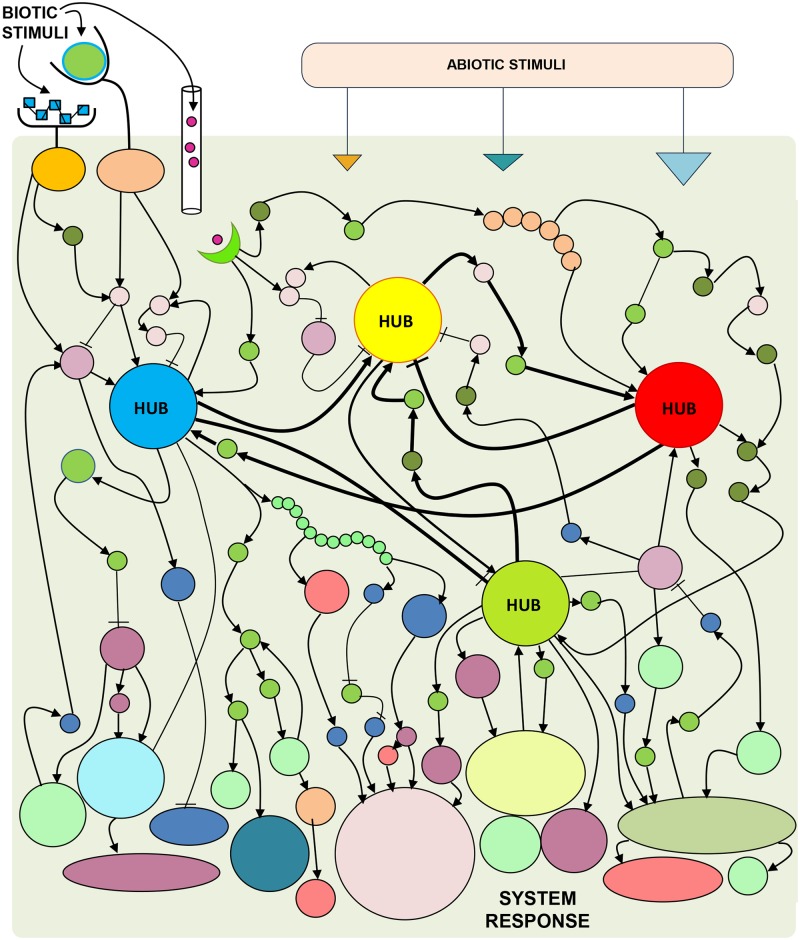
Fig 1. Combinations of system perturbations assist in discovering the mechanisms that drive complex biological system responses.

Complex systems, e,g., the immune system of an organism, are notably complicated in two ways: (1) they are tuned to respond differently to different system inputs, and (2) the system that mediates outputs as a function of inputs is full of network redundancy, which ensures operation under nonideal circumstances. Thus, learning the rules for how a complex system operates requires coincident, varied, and likely combinatorial external and internal perturbations to a system. Mild perturbations are likely buffered by the system; strong perturbations are the key. Complex systems often have numerous parts; how do we decide which parts should be perturbed? Network hubs—parts which integrate numerous signals and/or regulate many parts—are excellent candidates for an abbreviated parts list. We then monitor system behavior, in response to external perturbations, when different combinations of hubs have been rendered inoperable. Data from this monitoring can enable mathematical reconstruction of how major system parts are stimulated, influence each other, and modulate system output. These mathematical models are then used to direct further experiments, which leads to model refinement. Goals of iterative model building include: furthering our fundamental understanding of the system and predicting properties of the system relevant in applied settings. Image: conceptual diagram of a complex system that responds to system inputs (i.e., external perturbations).