Microscopic identification of the order parameter governing liquid–liquid transition in a molecular liquid

Significance

Liquid–liquid transition (LLT) in single-component liquids is one of the most mysterious phenomena in condensed matter. To understand this phase transition, it is essential to elucidate the order parameter governing it. We have succeeded in accessing the structural order parameter governing LLT by simultaneously measuring small- and wide-angle X-ray scattering during the process of LLT. We identify the order parameter to be the number density of locally favored structures, whose size is a few nanometers. This suggests that the order parameter is scalar and nonconserved. This finding sheds new light on the physical nature of this unconventional transition from one liquid to another.

Abstract

A liquid–liquid transition (LLT) in a single-component substance is an unconventional phase transition from one liquid to another. LLT has recently attracted considerable attention because of its fundamental importance in our understanding of the liquid state. To access the order parameter governing LLT from a microscopic viewpoint, here we follow the structural evolution during the LLT of an organic molecular liquid, triphenyl phosphite (TPP), by time-resolved small- and wide-angle X-ray scattering measurements. We find that locally favored clusters, whose characteristic size is a few nanometers, are spontaneously formed and their number density monotonically increases during LLT. This strongly suggests that the order parameter of LLT is the number density of locally favored structures and of nonconserved nature. We also show that the locally favored structures are distinct from the crystal structure and these two types of orderings compete with each other. Thus, our study not only experimentally identifies the structural order parameter governing LLT, but also may settle a long-standing debate on the nature of the transition in TPP, i.e., whether the transition is LLT or merely microcrystal formation.

Liquid-liquid transition (LLT) is an intriguing phenomenon in which a liquid transforms into another one via a first-order transition. This means that there can be more than two liquid states for a single-component substance. Despite its counterintuitive nature, there have recently been many pieces of experimental and numerical evidence for the existence of LLT, for various liquids such as water (1–5), aqueous solutions (6–8), triphenyl phosphite (9–12), l-butanol (13), phosphorus (14), silicon (15, 16), germanium (17), and ${\text{Y}}_2{\text{O}}_3$–${\text{Al}}_2{\text{O}}_3$ (18, 19). This suggests that the LLT may be rather universally observed for various types of liquids. However, none of the LLTs reported so far is free from criticisms (20, 21), mainly because these LLTs take place under experimentally difficult conditions [e.g., at high temperature and pressure (14, 15, 17–19)] or in a supercooled state below the melting point (1–3, 5–7, 9, 10), where the transition is inevitably contaminated by microcrystal formation. The latter is not limited to experiments but arises in numerical simulations, often causing many controversies [LLT (22–25) vs. crystallization (26–28)]. For ST2 water, however, this issue has recently been settled by an extensive simulation study by Palmer et al. (4).

One of the hottest and long-standing debates is on the nature of the transition found in a molecular liquid, triphenyl phosphite (TPP), by Kivelson and his coworkers (29). The transition is very easy to access experimentally, because it takes place at ambient pressure and at a temperature range between 230 and 210 K and the transformation speed is slow enough to follow the kinetics. Since the finding of this transition (29, 30), many researchers thus have been interested in this intriguing phenomenon and there have been hot discussions on the nature of the transition (20, 21). Some people interpreted this as a liquid-associated phenomenon (9, 10, 31, 32), but others interpret it differently. All of the controversies come from the fact that this transition accompanies microcrystal formation and thus the final state, which is called “glacial phase,” often contains microcrystallites. This led many researchers to explain the transition by non-LLT scenarios, which include a defect-ordered phase scenario predicted by a frustration limited domain theory (29, 30, 33, 34), a microcrystallization scenario (35–38), and a liquid-crystal or plastic-crystal phase scenario (39). Each scenario captures a certain feature of the glacial phase, but fails in explaining all of the experimental results in a consistent manner. Similar situations are often seen in other candidates of LLTs, such as l-butanol [LLT (13) vs. microcrystallization (40–43)], confined water [LLT (5) vs. other phenomena (44–46)], and aqueous solutions [LLT (6, 7) vs. microcrystallization (8, 28, 47, 48)]. For TPP, however, some pieces of experimental evidence supportive of the LLT scenario rather than the microcrystallization scenario have recently been reported (11, 12).

We propose a two-order-parameter (TOP) model of a liquid to explain LLT (20, 49). The main point of this model is that it is necessary to consider the spatiotemporal hierarchical nature of a liquid to understand LLT. More specifically, we argue that in addition to density order parameter $\mathit{\rho }$ describing a gas–liquid transition, we need an additional scalar order parameter S, which is the number density of locally favored structures (LFS). In this model, LLT is a consequence of the cooperative ordering of the scalar nonconserved order parameter S, i.e., the cooperative formation of LFS. In other words, LLT is regarded as a gas–liquid-like transition of LFS: one liquid is a gas state of LFS (low-S state), and the other is its liquid state (high-S state). Recently, it was proposed by Anisimov and coworkers (50, 51) that the thermodynamic ordering field conjugate to the order parameter is the conversion equilibrium constant, which further characterizes the nature of LLT. We explained our experimental observation of LLT in TPP in terms of this model (9, 10). We also studied the phase transition dynamics and the physical and chemical properties of the second liquid state (liquid II), which were also explained by the model (20, 21).

However, we have not had any direct experimental evidence for the formation of such LFS up to now; thus, an open question is, what is the relevant order parameter governing LLT, although the link of the order parameter to the enthalpy (9, 10), the refractive index (or, density) (9, 10, 29, 30), and the polarity associated with local molecular ordering (12) has been suggested for LLT in TPP. There have been structural studies on LLT by X-ray and neutron scattering measurements, focusing on local liquid structures at an inter- and intramolecular scale (36, 38, 52–54) and mesoscopic structures (34, 55). However, there has been no experimental evidence for the presence of locally favored structures, which characterize the liquid state uniquely, or the order parameter has still not been identified from a microscopic viewpoint.

Here we study the structural change of TPP during LLT by time-resolved small- and wide-angle X-ray scattering measurements, which cover a length scale from a single molecule size ($\sim$ 1 nm) to more than tens of nanometers. We show, to our knowledge, the first direct evidence for the presence of LFS and the temporal increase upon the liquid I-to-liquid II transformation. Furthermore, we also find an indication of the formation of microcrystallites during LLT. However, we reveal that LFS and microcrystallites have different sizes and growth kinetics, indicating that although they sometimes appear simultaneously during the process of LLT, LLT itself is driven by the formation of LFS and not by that of microcrystallites. We also discover that LFS are destroyed upon crystallization, clearly indicating not only that these two types of orderings are competing with each other but also that LFS is a structure unique to the liquid state. Our findings provide a comprehensive view on the long-standing controversy on the origin of the glacial phase, which was discovered by Kivelson and his coworkers (29, 30), and show that the fraction of LFS may be the relevant order parameter of LLT. This suggests that a liquid can have a spatiotemporal hierarchical structure at a low temperature, contrary to the common picture of a high-temperature liquid where the structure is random and homogeneous beyond the molecular size.

Results and Discussion

Results of Small-Angle X-Ray Scattering.

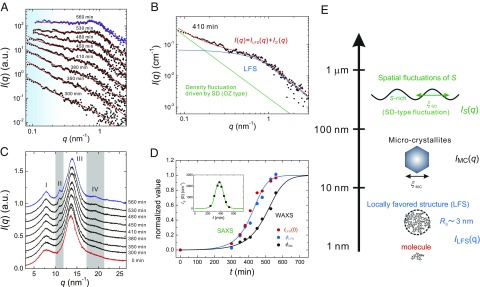
We show in Fig. 1A the temporal change of the scattering function $I\left(q\right)$ in a small-angle regime during LLT at the annealing temperature $T_{\text{a}}=$ 212 K. The experimental details are described in Materials and Methods. We quenched a liquid from $T=293$ K to $T_{\text{a}}$ within 5 min and then followed the time evolution of $I\left(q\right)$. The raw data covering not only a small-angle but also a wide-angle regime are shown in Fig. S1. $I\left(q\right)$ exhibits complex temporal evolution during LLT. In the final state of LLT at 560 min, there is a distinct Guinier regime (56) in $I\left(q\right)$, implying the existence of LFS. To analyze the $I\left(q\right)$ at a low-q region, we basically consider the following two contributions in the light of our TOP model (49): (i) scattering from an LFS, $I_{\text{LFS}}\left(q\right)$, and (ii) scattering from large-scale spatial fluctuations of the local number density of LFS, S, induced by the cooperativity in the formation of LFS, $I_S\left(q\right)$. The latter is related to the development of macroscopic spatial fluctuations observed during LLT with optical microscopy (9, 10) and light scattering (11): droplet structures for nucleation and growth (NG)-type transformation and large-scale continuous density fluctuations for spinodal decomposition (SD)-type transformation. These fluctuations can also be detected by X-ray scattering measurements because S should be coupled to the density $\mathit{\rho }$ (49). Note that the density is further proportional to the electron density. On the basis of this picture, we express $I\left(q\right)$ in a small-angle regime as follows (57):

$$I\left(q\right)=I_S\left(q\right)+I_{\text{LFS}}\left(q\right),$$ [1]

$$I_S\left(q\right)=\frac{I_S\left(0\right)}{1+q^2{\xi }_S^2},$$ [2]

$$I_{\text{LFS}}\left(q\right)=I_{\text{LFS}}\left(0\right)P\left(q\right)F\left(q\right).$$ [3]

Fig. 1.

Structural evolution during LLT. (A) Time evolution of $I\left(q\right)$ in a small-angle regime during LLT at $T_{\text{a}}=$ 212 K. The blue and black filled circles correspond to $I\left(q\right)$ of liquid II after the transformation (at 560 min) and in the transformation process, respectively. Here the contribution from wide-angle scattering [the tail of the peak at $q=$ 7.7 ${\text{nm}}^{-1}$ (see C)] is already subtracted from the original data. The red solid curves represent the best fits by Eqs. 1–3. The light blue regime shows the contribution from large-scale density fluctuations associated with SD-type LLT. (B) An example of the fitting at 410 min. The total scattering function (red solid line) is decomposed into the contribution of LFS (blue solid line) and that of large-scale density fluctuations (green solid line). (C) Time evolution of $I\left(q\right)$ in a wide-angle regime. The red and blue curves correspond to $I\left(q\right)$ at 0 min and 560 min, respectively, and black curves to $I\left(q\right)$ in the transformation process. Here we label the peaks of $I\left(q\right)$ as I, II, III, and IV from a lower to higher wavenumber. Peaks II and IV highlighted by the gray belts appear and grow during LLT. (D) Time evolutions of the normalized $I_{\text{LFS}}\left(0\right)$ (blue filled circles), ${\varphi }_{\text{LFS}}$ (red filled circles), and ${\varphi }_{\text{MC}}$ (black filled circle). The data are fitted by a theoretical prediction for the development of a nonconserved order parameter (60). The blue solid line represents the best fit to both $I_{\text{LFS}}\left(0\right)$ and ${\varphi }_{\text{LFS}}$ and the black solid line is the best fit to ${\varphi }_{\text{MC}}$. (Inset) Temporal change of $I_S\left(0\right)$. The green line is a guide to the eye. Note that the data in A and C are vertically shifted for clarity. (E) Schematic figure representing the hierarchical structure of a liquid state of TPP.

First we discuss the scattering component $I_S\left(q\right)$. Here we assume the Ornstein–Zernike (OZ) correlation function for large-scale density fluctuations observed below $T_{\text{SD}}$. The spinodal temperature $T_{\text{SD}}$ of LLT is determined as 215.5 K (10). $I_S\left(0\right)$ represents the intensity of the S fluctuations and ${\xi }_S$ the correlation length (Fig. 1E). Because the correlation length ${\xi }_S$ is much longer than the length scale that is covered by our small-angle X-ray scattering measurements, we set ${\xi }_S=1$ $\mathit{\mu }$ m and ignored its temporal change. This choice of ${\xi }_S$ has no effects on our analysis because ${\xi }_S\gg 1/q$ for our q range.

Next we discuss the scattering component $I_{\text{LFS}}\left(q\right)$. In Eq. 3, $P\left(q\right)$ is the form factor of LFS and $F\left(q\right)$ is the structure factor. The prefactor $I_{\text{LFS}}\left(0\right)$ is proportional to the number density of LFS (S) and the square of the electron density difference between LFS and its surrounding normal liquid structures. In Fig. 1A, we confirm that $I\left(q\right)$ of liquid II after the transformation does not obey the Porod law $\left(I\left(q\right)\propto q^{-4}\right)$ but its q dependence is weaker, indicating that the LFS is a low-dimensional cluster without a sharp flat interface. Thus, we describe $P\left(q\right)$ as nearly spherical clusters with rough interface (see SI Text for a possible other shape of clusters) by the following function:

$$P\left(q\right)=4\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}C\left(r\right)\frac{\text{sin}\left(qr\right)}{qr}{r}^{2}dr},$$ [4]

$$C\left(r\right)=r^{d_{\text{f}}-d}\exp \left(-r/{\xi }_{\text{LFS}}\right),$$ [5]

where $C\left(r\right)$ is the density autocorrelation function, $d_{\text{f}}$ the mass fractal dimension of clusters (extent of molecular packing in a cluster), d the spatial dimension $\left(d=3\right)$, and ${\xi }_{\text{LFS}}$ the characteristic cluster size which can be transformed to the gyration radius of LFS, $R_{\text{g}}$, by the following relation: $R_{\text{g}}=\sqrt{d_{\text{f}}\left(d_{\text{f}}+1\right)/2}\hspace{0.17em}{\xi }_{\text{LFS}}$ (57). The independence of ξ_LFS (or R_g) on T_a (see Table S1) indicates that ξ_LFS is the characteristic size of LFS, or the bare correlation length of the order parameter (S) fluctuations. We note that the spatial correlation length of the LFS concentration is given by ξ_S.

Furthermore, in the Guinier regime, $I\left(q\right)$ has a shallow dip around $q=$0.7 ${\text{nm}}^{-1}$ [see, e.g., the data at 560 min in Fig. 1A (see also the data in Fig. 4A) and Fig. S2], indicating the existence of the hard-core–like repulsive interaction between LFS. The resulting spatial correlation is expressed by a structure factor $F\left(q\right)$ in $I_{\text{LFS}}\left(q\right)$. To take the excluded volume effect of LFS into account, we use a simple hard-sphere model and solve the Percus–Yevick closure. Then we obtain $F\left(q\right)$ as $F_{\text{PY}}\left(q,R_{\text{g}},{\varphi }_{\text{LFS}}\right)$, whose complete formula is shown in, e.g., refs. 58, 59. Here ${\varphi }_{\text{LFS}}$ is the (excluded) volume fraction of LFS (note that ${\varphi }_{\text{LFS}}\propto S$). At first, we analyze $I\left(q\right)$ of liquid II (at 560 min, where the transformation is completed) to obtain $R_{\text{g}}$ and $d_{\text{f}}$ of LFS. We note that for this final state there is no contribution of $I_S\left(q\right)$ and the scattering signal can be described by $I_{\text{LFS}}\left(q\right)$ alone. This is justified by the experimental fact that liquid II finally becomes macroscopically homogeneous after the transformation $\left(I_S\left(q\right)=0\right)$ (9–11). We obtain $R_{\text{g}}=3.3$ nm and $d_{\text{f}}=2.28$. These values of the gyration radius $R_{\text{g}}$ and the mass fractal dimension $d_{\text{f}}$ suggest that the structure is LFS made of a small number of molecules and has a complex shape with a rough surface, and not a microcrystallite, because the crystal should have a rather sharp interface. We use these values of $R_{\text{g}}$ and $d_{\text{f}}$ as the fixed parameters for fitting during the transformation process in the light of our two-state model (49). The red solid lines in Fig. 1A indicate the results of the fitting. The above model functions can successfully reproduce the experimental data. An example of the fitting for the data at 410 min is shown in Fig. 1B. The fact that the LFS cluster has a rough interface indicates that the LFS is made of at least several molecules and thus has a complex shape.

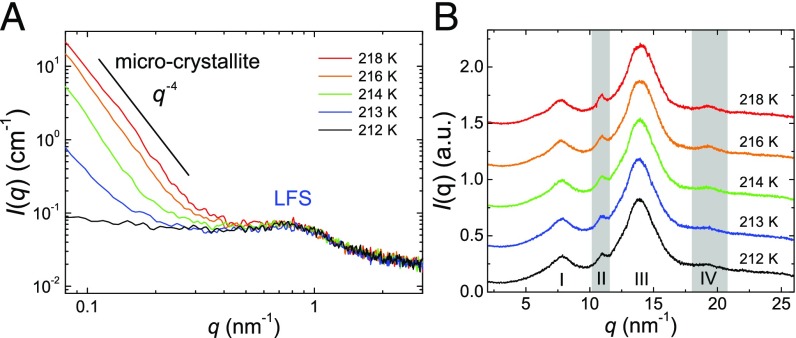
Fig. 4.

Crystallization process from a glassy state of liquid II. (A) Temperature dependence of $I\left(q\right)$ of liquid II (prepared at $T_{\text{a}}=$ 214 K) in a small-angle regime, in the heating process. The increase of $I\left(q\right)$ around $q=$ 0.3 ${\text{nm}}^{-1}$ below 228 K means that the effect of $F\left(q\right)$ gradually weakens (the decrease of ${\varphi }_{\text{LFS}}$) upon heating. (B) The same as A in a wide-angle regime. The data are vertically shifted and the data for 233 K are displayed separately for clarify. (Inset) Enlarged figure of the peak II region. (C) Temperature dependence of $I_{\text{LFS}}\left(0\right)$ (red filled circles) and ${\varphi }_{\text{LFS}}$ (blue filled circles) obtained from the analysis of the result in A.

Results of Wide-Angle X-Ray Scattering.

Next we show the time evolution of $I\left(q\right)$ in a wide-angle regime in Fig. 1C, which is measured simultaneously with $I\left(q\right)$ at a low-q range shown in Fig. 1A. We find small changes in $I\left(q\right)$ around $q=$ 10.9 ${\text{nm}}^{-1}$ and q = 19.2 ${\text{nm}}^{-1}$ (highlighted by the gray bars), whereas no change is found in the other part of $I\left(q\right)$ as a function of time. We characterize the temporal change of $I\left(q\right)$ in a wide-angle regime by ${\varphi }_{\text{MC}}=A_{\text{I}}/\left(A_{\text{I}}+A_{\text{II}}\right)$, where $A_{\text{I}}$ and $A_{\text{II}}$ are the integral intensity of peak I and II (see Fig. 1C for the assignments), respectively. We assume that peak I comes from the normal liquid structure and peak II from a new structure formed during LLT. We show in Fig. 1D the time evolutions of $I_{\text{LFS}}\left(0\right)$, ${\varphi }_{\text{LFS}}$, and ${\varphi }_{\text{MC}}$ normalized by their values at the final state (liquid II), respectively, which are listed in Table S1. We find that the time evolutions of $I_{\text{LFS}}\left(0\right)$ and ${\varphi }_{\text{LFS}}$ agree well with each other despite the fact that the fittings are made independently. This proportionality between the intensity of scattering from LFS, $I_{\text{LFS}}\left(0\right)$, and the volume faction of LFS, ${\varphi }_{\text{LFS}}$, indicates that LFS changes neither their size nor electron density but only their number density increases with time. We can also see that the $I_S\left(0\right)$ shows a peak around 380 min (Fig. 1D, Inset), which is consistent with the growth and decay of S fluctuations observed with phase contrast microscopy (10) as well as time-resolved light-scattering measurements (11). Interestingly, the time evolution of ${\varphi }_{\text{MC}}$ is significantly slower than that of $I_{\text{LFS}}\left(0\right)$ and ${\varphi }_{\text{LFS}}$. The delay time $\mathrm{\Delta }\tau ={\tau }_{\text{MC}}-{\tau }_{\text{LFS}}$ is estimated as 103 min at $T_{\text{a}}=212$ K, where ${\tau }_{\text{LFS}}$ and ${\tau }_{\text{MC}}$ are, respectively, the times when the normalized values of $I_{\text{LFS}}\left(0\right)$ and ${\varphi }_{\text{MC}}$ reach 1/2. We previously interpreted that the newly emerging peaks II and IV were associated with LFS (54). However, this delay suggests that these small peaks emerging in a wide-angle regime are not associated with LFS but with something else.

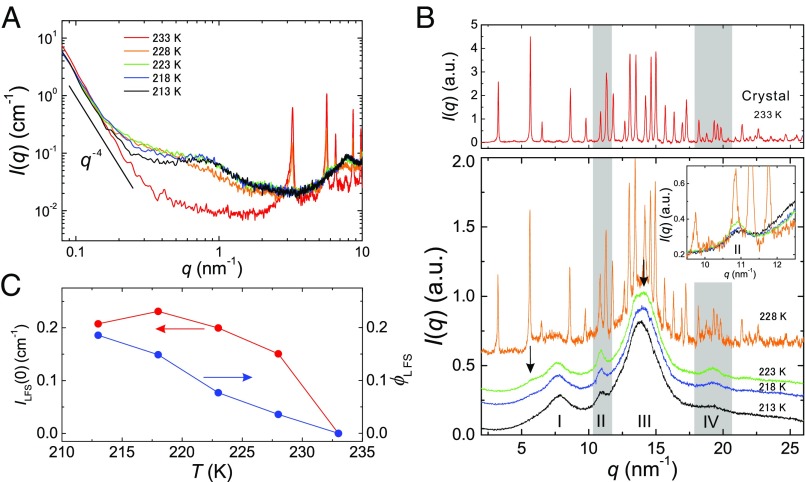
The question then is, what structure is responsible for the change of $I\left(q\right)$ in a wide-angle regime? To answer this, we focus on $I\left(q\right)$ of liquid II prepared at higher $T_{\text{a}}$. Fig. 2A shows $T_{\text{a}}$ dependence of $I\left(q\right)$ in a small-angle regime. We find that $I\left(q\right)$ below 0.4 ${\text{nm}}^{-1}$ increases with increasing $T_{\text{a}}$ and obeys the Porod law except at $T_{\text{a}}=$ 212 K, whereas $I\left(q\right)$ above 0.4 ${\text{nm}}^{-1}$, which is the contribution from the LFS, shows little change. The Porod law regime at low q indicates the presence of additional structures, which have a sharp interface in liquid II and whose size is much larger than that of the LFS. The most probable candidate is microcrystallites. Then, the increase of this contribution with increasing $T_{\text{a}}$ indicates that more microcrystallites are formed at higher $T_{\text{a}}$. This interpretation is also supported by the results of our calorimetric, optical birefringence, and light-scattering measurements (9, 11, 60), which all indicate the formation of microcrystallites and the increase in their amount with an increase in $T_{\text{a}}$. Next we show $T_{\text{a}}$ dependence of $I\left(q\right)$ in a wide-angle regime in Fig. 2B. We find that peaks II and IV are more pronounced for higher $T_{\text{a}}$ (see also the values of ${\varphi }_{\text{MC}}$ in Table S1). Together with the above, it may be natural to interpret that newly emerged peaks II and IV originate mainly from microcrystallites, although some contribution from LFS might be contained. We note that the size of LFS may be too small for the spatial correlation within it to cause a distinct scattering peak in the wide-angle regime. Thus, we conclude that LFS and microcrystallites have different length scales (Fig. 2A) and different formation kinetics (Figs. 1D and 3C). Although the formation of microcrystallites in the glacial phase, i.e., the glassy state of liquid II, might look counterintuitive, this is reasonably explained by a scenario that microcrystallites are selectively nucleated at the growth front of a liquid II droplet but stop growing after being included in the droplet (see SI Text for the details).

Fig. 2.

Microcrystallites coexisting with LFS. (A) $T_{\text{a}}$ dependence of $I\left(q\right)$ of liquid II in a small-angle regime. The scattering at $q>0.4$ ${\text{nm}}^{-1}$ comes from LFS, whereas the scattering at $q<0.4$ ${\text{nm}}^{-1}$ comes from microcrystallites. Here the slope of the Porod law $\left(I\left(q\right)\propto q^{-4}\right)$ is also indicated. (B) $T_{\text{a}}$ dependence of $I\left(q\right)$ in a wide-angle regime.

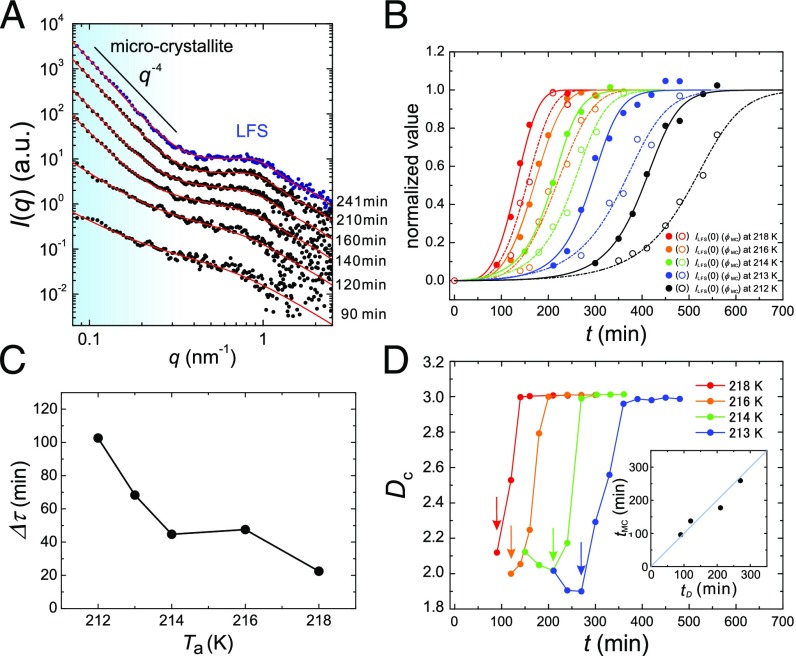
Fig. 3.

Structural evolution during LLT at various $T_{\text{a}}$ s. (A) Time evolution of $I\left(q\right)$ in a small-angle regime during LLT at $T_{\text{a}}$=218 K. The data are vertically shifted for clarity. The blue filled circles show $I\left(q\right)$ of liquid II at 241 min. The contribution from the wide-angle scattering is subtracted from the data as in Fig. 1A. The red solid curves represent the best fit of the relation $I\left(q\right)=I_{\text{LFS}}\left(q\right)+I_S\left(q\right)+I_{\text{MC}}\left(q\right)$ with Eqs. 6 and 7. The shoulder around 1 ${\text{nm}}^{-1}$ is the scattering contribution from LFS. The scattering signal in the light blue region is mainly from long-range density fluctuations associated with LLT in the early stage, and from microcrystallites in the late stage. (B) Time evolutions of the normalized $I_{\text{LFS}}\left(0\right)$ and ${\varphi }_{\text{MC}}$ for various $T_{\text{a}}$ s. For 212, 213, and 214 K, we used an equation describing SD-type ordering as the fitting function (20). For 216 and 218 K, where NG-type LLT proceeds, we used a Kolmogolov–Avrami equation to describe the evolution (20). The solid curves indicate the best fit to $I_{\text{LFS}}\left(0\right)$ whereas the dash–dot curves correspond to ${\varphi }_{\text{MC}}$. (C) $T_{\text{a}}$ dependence of the delay time, $\mathrm{\Delta }\tau ={\tau }_{\text{MC}}-{\tau }_{\text{LFS}}$. See text for the definition of ${\tau }_{\text{LFS}}$ and ${\tau }_{\text{MC}}$. (D) $T_{\text{a}}$ dependence of the temporal change of $D_{\text{c}}$. Each arrow indicates the onset of the change in $D_{\text{c}}$, i.e., the onset of microcrystal formation. (Inset) Relation between the onset time of ${\varphi }_{\text{MC}}$, $t_{\text{MC}}$, and that of $D_{\text{c}}$, $t_{\text{D}}$, indicating the relation $t_{\text{MC}}\sim t_{\text{D}}$.

Formation of Locally Favored Structures and Microcrystallites.

To elucidate the ordering behavior during LLT in more detail, we also investigate the temporal evolution of $I\left(q\right)$ at various $T_{\text{a}}$. As shown in Fig. 2A, more microcrystallites are formed during LLT at higher $T_{\text{a}}$. This indicates that when analyzing $I\left(q\right)$ at low q, we need to consider an additional contribution from microcrystallites in Eq. 1: $I\left(q\right)=I_{\text{LFS}}\left(q\right)+I_S\left(q\right)+I_{\text{MC}}\left(q\right)$, where $I_{\text{MC}}\left(q\right)$ is the contribution from microcrystallites. In Fig. 3A, we show as an example the time evolution of $I\left(q\right)$ in a small-angle regime during the LLT at $T_{\text{a}}=$ 218 K. Actually, $I\left(q\right)$ at $q<$ 0.4 ${\text{nm}}^{-1}$ increases rapidly with time in the late stage and obeys the Porod law in the final state. However, it is almost impossible to separate $I_{\text{MC}}\left(q\right)$ and $I_S\left(q\right)$ due to the limitation of our q range. So, we need to make an assumption. Here we assume that the scattering from microcrystallites is much more dominant than that from spatial fluctuations of the concentration of LFS. This should be reasonable because (i) the density change is far more significant for crystallization than for the formation of LFS and (ii) the correlation length of microcrystallites is much shorter than that of LFS spatial fluctuations and, thus, the former has a larger scattering contribution than the latter in our q range. Then, we can assume

$$I\left(q\right)\sim I_{\text{MC}}\left(q\right)=I_{\text{MC}}\left(0\right)4\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}C\left(r\right)\frac{\text{sin}\left(qr\right)}{qr}{r}^{2}dr},$$ [6]

$$C\left(r\right)=r^{D_c-d}\exp \left(-r/{\xi }_{\text{MC}}\right),$$ [7]

where D_c and ξ_MC are the spatial dimensionality and the characteristic size of microcrystallites, respectively. We tentatively set ${\xi }_{\text{MC}}$ as 300 nm although there is no firm basis for this. What we can be confident about is the relation of ${\xi }_{\text{LFS}}\left(\sim 1.7\hspace{0.17em}\text{nm}\right)<{\xi }_{\text{MC}}<{\xi }_S$ (see also refs. 9, 10). This relation, although not rigorous, is sufficient for estimating the size of LFS. The results of the fitting are indicated by red solid lines in Fig. 3A, indicating that the experimental data can be well described by the above model. The fittings yield $R_{\text{g}}$, $d_{\text{f}}$, and $I_{\text{LFS}}\left(0\right)$ of the LFS as $\sim$3 nm, $\sim$2.3, and $\sim$0.17 ${\text{cm}}^{-1}$, respectively, independent of $T_{\text{a}}$ (Table S1). This stability of LFS suggests that it is a well-defined local structural element and its number density (S) can be regarded as the order parameter governing LLT. This order parameter monotonically increases during LLT, indicating its nonconserved nature, consistent with the two-order-parameter model (20, 49).

In Fig. 3B, we show the time evolutions of the normalized $I_{\text{LFS}}\left(0\right)$ and ${\varphi }_{\text{MC}}$ during the transformation at various $T_{\text{a}}$ s. The values used for the normalization at each $T_{\text{a}}$ are listed in Table S1. The sequential ordering, LLT first and then microcrystal formation, observed at 212 K (Fig. 1C), is also confirmed for all $T_{\text{a}}$ s irrespective of the type of phase transformation, NG- or SD type. As shown in Fig. 3C, $\mathrm{\Delta }\tau$ monotonically increases with decreasing $T_{\text{a}}$. We also find an interesting relation between $D_{\text{c}}$ and ${\varphi }_{\text{MC}}$ in the transformation process. Fig. 3D shows the temporal change of $D_{\text{c}}$ during LLT, indicating a sharp change of $D_{\text{c}}$ from 2 to 3 (see the arrows in Fig. 3D). Note that $D_{\text{c}}=$ 3 in Eqs. 6 and 7 corresponds to the Debye–Anderson–Brumberger function whose q dependence obeys the Porod law, representing the scattering from randomly distributed clusters with a sharp interface (61). This suggests that the onset of the change in $D_{\text{c}}$ reflects the formation of microcrystallites in the process. We also confirm that this onset time $t_{\text{D}}$ is in good agreement with that of ${\varphi }_{\text{MC}}$, $t_{\text{MC}}$ (Fig. 3D, Inset), again suggesting a strong correlation between the formation of microcrystallites and the changes in a wide-angle regime in the annealing process (Fig. 2A and B).

In the early stage, $D_{\text{c}}$ has the value of about 2, independent of $T_{\text{a}}$. In Eqs. 6 and 7, this corresponds to the OZ correlation function whose formula is already given in Eq. 2 although the value of ${\xi }_{\text{MC}}$ should be different from that of ${\xi }_S$. Thus, it is reasonable to consider that $D_{\text{c}}=$ 2 does not come from $I_{\text{MC}}\left(q\right)$ but rather from $I_S\left(q\right)$. We note that these two length scales cannot be distinguished in our measurements because of the limited q range. For NG-type LLT (at 216 and 218 K), however, $D_{\text{c}}$ is expected to be 3 because a droplet structure with a sharp interface is observed with phase contrast microscopy. This discrepancy may be caused by the experimental limitation that our q range is too high compared with the characteristic wavenumber of such a macroscopic structure. Thus, we can access only the tail part of the scattering from droplets, which may be a cause for a small value of $D_{\text{c}}$ even for NG-type LLT.

Crystallization Process of Liquid II.

Finally, we study the crystallization process of liquid II upon heating, focusing on the behaviors of LFS and microcrystallites. In Fig. 4A and B, we show $I\left(q\right)$ of liquid II in a small-angle and wide-angle regime, respectively, during the heating process of liquid II formed at $T_{\text{a}}$ = 214 K. There are only minor changes in a small-angle regime below 223 K unlike the case in the annealing measurement (Fig. 2A), whereas peaks II and IV in a wide-angle regime constantly grow upon heating, as in the case of Fig. 2B. Above 228 K, drastic changes start to take place in both small-angle and wide-angle regimes: $I\left(q\right)$ of LFS (0.3 $<q<$ 3 ${\text{nm}}^{-1}$) starts to decrease at 228 K and finally disappears at 233 K. We note that these behaviors are linked to the emergence of many Bragg peaks at 228 K and their complete developments at 233 K in a wide-angle regime, respectively. We quantitatively analyzed this change in the small-angle regime, using the above model function. The results are shown in Fig. 4C. Both $I_{\text{LFS}}\left(0\right)$ and ${\varphi }_{\text{LFS}}$ decrease upon heating, suggesting that the crystallization process proceeds while destroying LFS. The difference in the T dependence between $I_{\text{LFS}}\left(0\right)$ and ${\varphi }_{\text{LFS}}$ may be due to inhomogeneous distribution of LFS under coexistence with crystals. In particular, we find the coexistence of the Bragg peaks and the LFS halo at 228 K, suggesting that the liquid state can survive as long as LFS persist. This indicates that the LFS act against the growth of microcrystallites and have frustration effects on crystallization. Similar situations were reported by numerical simulations and experiments of systems with competing orderings (20, 62, 63). The Bragg peak at $q=10.8$ ${\text{nm}}^{-1}$ (at 228 K) continuously grows from peak II resulting from microcrystallites (Fig. 4B, Inset), suggesting that large (bulk) crystals may be formed from microcrystallites. Although the growth of microcrystallites is detected only in a wide-angle regime during the heating process, its sign is expected to be observed in a small-angle regime but below our q range. We note that the little change in $I\left(q\right)$ below $q<0.2$ ${\text{nm}}^{-1}$ in Fig. 4A is not necessarily inconsistent with the growth of microcrystallites, because the growth may cause the change only in the Guinier regime and not in the Porod regime. This point should be studied carefully in the future by accessing a lower q range.

Another important point is the structural characteristic of microcrystallites. At 223 K, i.e., even at a rather higher temperature, besides peaks II and IV we observe only a few broad peaks (shown by the arrows in Fig. 4B), which are attributed to microcrystallites. This implies that microcrystallites are not big enough to produce sharp diffraction peaks. According to the X-ray and ab initio study by Hernandez et al. (64), the unit cell of TPP crystal has a disk-like shape (lattice constant: $a=$ 37.77 Å, $b=$ 32.71 Å, $c=$ 5.729 Å). This may explain why the scattering from the $a-b$ plane is much weaker compared with that from the c direction [e.g., peaks II and IV (64)]: Strong correlation along the $a-b$ plane of the crystal requires a much longer length than that along the c direction. So, small microcrystallites can produce only a part of the Bragg peaks of the bulk crystal.

Conclusions

To conclude, we show, to our knowledge, the first experimental evidence that nanometer-size locally favored structures are formed upon LLT and their number density is the order parameter of LLT, although generality of a link of the formation of LFS to LLT and the origin of its cooperativity still need to be clarified. Our study also indicates that the controversy on the nature of the transformation in TPP originates from the fact that two different types of orderings, LLT and microcrystal formation, proceed almost simultaneously. We successfully separate the two types of orderings by directly following the process of their formation: LLT takes place first, followed by crystallization. We speculate that the formation of microcrystallites during LLT observed in these systems is a consequence of a lower crystal–liquid interfacial energy for liquid II than for liquid I, which was confirmed for TPP (65). The interface tension should be associated with the spatial gradient of the order parameters (density and local structure) across the interface. We speculate that for TPP a smaller density difference of liquid II/crystal than liquid I/crystal lowers the nucleation barrier. The formation of microcrystallites associated with LLT is also observed in other liquids: l-butanol (13), germanium (17), and aqueous organic solutions (6–8). The above scenario might be widely applicable to these cases.

Materials and Methods

The sample used in this measurement is TPP purchased from Acros Organics and used after extracting only a crystallizable part to remove impurities. Time-resolved small- and wide-angle X-ray scattering (SWAXs) measurements were performed by using SAXSess camera (Anton Paar) in the q range from 0.08 ${\text{nm}}^{-1}$ to 27 ${\text{nm}}^{-1}$. Because the collimating system in this camera is of line-focus type, raw data (particularly in a small-angle regime) are smeared (57). We desmeared raw scattering data, or transformed raw data to their ideal scattering profile, which should be obtained from an ideal point focus system whose primary beam is expressed by the delta function, using the primary beam profile and Saxquant 3.0 software. We determined the absolute scattering intensity by using water as the reference. The value of the scattering intensity at $q=0$ of water is known as $I\left(0\right)=0.01632$ ${\text{cm}}^{-1}$ at 293 K (66). The X-ray exposure time is 10 min in all measurements, which is short enough compared with the entire transformation process. The measurement temperature in the capillary cell is calibrated by the melting point of n-octane (217 K). The contribution of scattering from a capillary tube in which a sample is sealed is subtracted from scattering data.