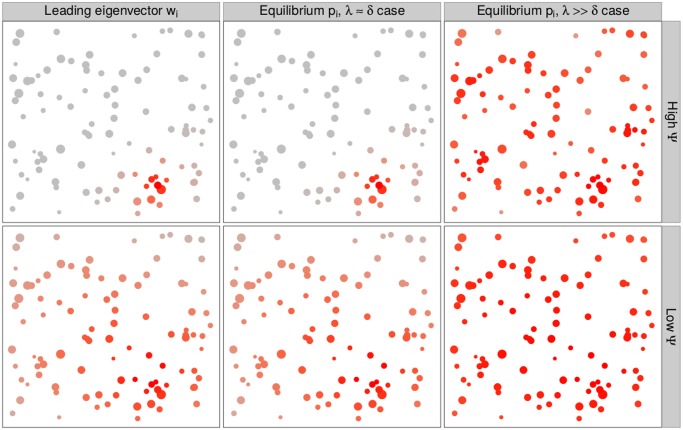
Fig 4. Spatial localization of metapopulations close to extinction.

The metapopulation can persist in two different regimes: for small n _e(1+σ ²), and therefore small λ, the leading eigenvector (i.e., that associated with λ) is highly heterogeneous (high Ψ, top left), while for large n _e(1+σ ²), all patches have roughly the same eigenvector component (low Ψ, bottom left). When the metapopulation is close to extinction (middle column, λ ≈ δ), the equilibrium values p _i are well approximated by the eigenvector component w _i. When the eigenvector is heterogeneous, the metapopulation is maintained by few patches with high probability of persistence (those with high w _i). The interesting feature is that these patches are spatially localized, so that a small region of the landscape contributes disproportionately to persistence. This is not the case when λ ≫ δ, in which case multiple eigenvectors influence p, resulting in an almost uniform distribution of the p _i (right column).