Abstract
Causal mediation analysis uses a potential outcomes framework to estimate the direct effect of an exposure on an outcome and its indirect effect through an intermediate variable (or mediator). Causal interpretations of these effects typically rely on sequential ignorability. Because this assumption is not empirically testable, it is important to conduct sensitivity analyses. Sensitivity analyses so far offered for this situation have either focused on the case where the outcome follows a linear model or involve nonparametric or semiparametric models. We propose alternative approaches that are suitable for responses following generalized linear models. The first approach uses a Gaussian copula model involving latent versions of the mediator and the final outcome. The second approach uses a so-called hybrid causal-observational model that extends the association model for the final outcome, providing a novel sensitivity parameter. These models, while still assuming a randomized exposure, allow for unobserved (as well as observed) mediator-outcome confounders that are not affected by exposure. The methods are applied to data from a study of the effect of mother education on dental caries in adolescence.
Keywords: Causal inference, Copula, Interaction, Mediation analysis, Mediation formula, Potential outcome, Structural equations model
1. Introduction
Mediation analysis has become popular as an approach for studying the mechanisms through which a treatment or exposure affects an outcome. In practice, mediation analysis utilizes one or more measured intermediate variables (or mediators) hypothesized to lie on the causal pathway between the exposure and the outcome. Typically, the analysis involves the decomposition of the overall exposure effect into a direct effect and an indirect (mediation) effect occurring through one or more intermediate variables.
A classical approach to mediation analysis involves the fit of linear regression models for the outcome and mediator (Baron and Kenny, 1986). Recently, causal model (potential outcomes) approaches have been developed that provide causally interpretable mediation effects under flexible situations, including generalized linear models and models with interactions (Robins and Greenland, 1992; Albert, 2008; Imai and others, 2010b).
One very general approach to causal mediation analysis is based on the mediation formula (Imai and others, 2010b; Albert and Nelson, 2011; Pearl, 2012). Although a nonparametric version of this method is possible (Imai and others, 2010b), a very general and practical use of the mediation formula is via parametric models. Particular applications of the parametric mediation formula are in several recent papers (Wang and Albert, 2012; Wang and others, 2013).
The mediation formula, which provides a key tool for the methods to be presented in this paper, is based on the potential outcomes framework. Some basic definitions and notation for this framework are as follows. We let 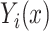 denote the potential outcome for (response variable)
denote the potential outcome for (response variable) 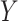 if causal factor
if causal factor 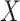 were set to level
were set to level 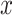 for individual
for individual 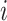 . Note that we will sometimes drop the subscript
. Note that we will sometimes drop the subscript 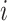 when not needed for clarity. The central problem of causal inference is that a response,
when not needed for clarity. The central problem of causal inference is that a response, 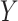 , for any given individual, is observed (at a given time) for only one level of the exposure
, for any given individual, is observed (at a given time) for only one level of the exposure 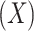 . Potential outcomes for exposure levels not actually observed are referred to as counterfactuals. To define mediation effects, we use nested potential outcomes. For example,
. Potential outcomes for exposure levels not actually observed are referred to as counterfactuals. To define mediation effects, we use nested potential outcomes. For example, 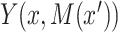 denotes the potential outcome for
denotes the potential outcome for 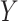 if exposure,
if exposure, 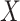 , were set to
, were set to 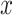 , but the mediator,
, but the mediator, 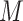 , set to its potential outcome if
, set to its potential outcome if 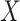 were set to
were set to 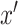 . We let
. We let 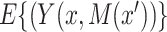 denote the average of this potential outcome over a specified population. Then we define the direct and indirect effects, respectively, as
denote the average of this potential outcome over a specified population. Then we define the direct and indirect effects, respectively, as
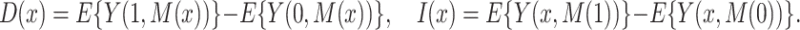 |
(1.1) |
Note that 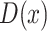 and
and  represent “natural” direct and indirect effects whereby the mediator,
represent “natural” direct and indirect effects whereby the mediator, 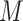 , is set to the value (potential outcome) that would “naturally” be observed under the specified exposure level. These estimands are in contrast to those of “controlled” direct and indirect effects whereby
, is set to the value (potential outcome) that would “naturally” be observed under the specified exposure level. These estimands are in contrast to those of “controlled” direct and indirect effects whereby 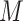 is fixed at a particular common value. The total effect,
is fixed at a particular common value. The total effect, 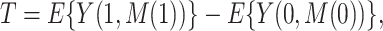 can be written as
can be written as 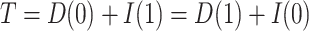 , demonstrating that the natural direct and indirect effects represent an exact decomposition of the total exposure effect.
, demonstrating that the natural direct and indirect effects represent an exact decomposition of the total exposure effect.
A key assumption in the identification of the natural direct and indirect effects (as used, e.g., by Imai and others, 2010b) is sequential ignorability. This assumption (discussed in detail in Section 2 below) comprises two conditions loosely stated as follows: (i) there are no unobserved confounders of the 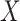 –
–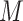 or
or 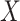 –
–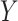 relationships and (ii) there are no unobserved (baseline or post-exposure)
relationships and (ii) there are no unobserved (baseline or post-exposure) 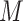 –
–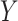 confounders. Unfortunately, these assumptions are not testable, although the first condition can sometimes be justified by the design, namely, when the exposure or treatment is randomly assigned or a sufficient set of prognostic baseline variables measured. The second part of the assumption, however, is generally difficult to make with confidence due to the possibility of unobserved
confounders. Unfortunately, these assumptions are not testable, although the first condition can sometimes be justified by the design, namely, when the exposure or treatment is randomly assigned or a sufficient set of prognostic baseline variables measured. The second part of the assumption, however, is generally difficult to make with confidence due to the possibility of unobserved 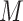 –
–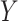 confounders. For this reason, a number of scholars (including Imai and others, 2010b) emphasize the importance of conducting a sensitivity analysis to accompany mediation effect estimates.
confounders. For this reason, a number of scholars (including Imai and others, 2010b) emphasize the importance of conducting a sensitivity analysis to accompany mediation effect estimates.
Approaches to sensitivity analysis offered in the past (Imai and others, 2010b) have often relied on linear or linearizable (e.g., probit) models. In these cases, sequential ignorability amounts to assuming a zero correlation between the error terms for the 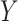 and
and 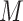 models. Imai and others (2010b) proposed a sensitivity analysis that examines the impact of varying this correlation, and Imai and others (2010a) extended this approach to a binary outcome using a probit regression model. VanderWeele (2010) presented a general nonparametric methodology that considered an unobserved confounder between the final outcome and mediator. Although simple bias formulae are provided under simplifying assumptions, more generally, this approach may require complex specifications of quantities involving the distribution of (or distributions that condition on) one or more confounders. Hafeman (2011) simplified the required specifications but limited the sensitivity analysis to the case of binary variables (exposure, mediator, and outcome). Recent contributions include Tchetgen Tchetgen and Shpitser (2012) who proposed a double robust semiparametric approach, and VanderWeele and Chiba (2014) who provided a nonparametric approach allowing for unobserved
models. Imai and others (2010b) proposed a sensitivity analysis that examines the impact of varying this correlation, and Imai and others (2010a) extended this approach to a binary outcome using a probit regression model. VanderWeele (2010) presented a general nonparametric methodology that considered an unobserved confounder between the final outcome and mediator. Although simple bias formulae are provided under simplifying assumptions, more generally, this approach may require complex specifications of quantities involving the distribution of (or distributions that condition on) one or more confounders. Hafeman (2011) simplified the required specifications but limited the sensitivity analysis to the case of binary variables (exposure, mediator, and outcome). Recent contributions include Tchetgen Tchetgen and Shpitser (2012) who proposed a double robust semiparametric approach, and VanderWeele and Chiba (2014) who provided a nonparametric approach allowing for unobserved 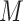 –
–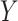 confounders affected by
confounders affected by 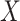 . A limitation of the latter two methods is that the number of sensitivity parameters increases with the dimensionality of
. A limitation of the latter two methods is that the number of sensitivity parameters increases with the dimensionality of 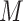 , making these approaches difficult when
, making these approaches difficult when 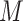 is not binary.
is not binary.
In the present paper, we propose two new approaches to sensitivity analysis designed to accommodate different types of variables, each assumed to follow a generalized linear model. The first approach uses a Gaussian copula model for the joint distribution of potential outcomes for 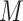 and
and 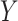 . Wang and others (2013) used a similar idea but made stronger assumptions than those of the present approach, resulting in a different derived model. The second approach considers a “hybrid” model that extends the association model for
. Wang and others (2013) used a similar idea but made stronger assumptions than those of the present approach, resulting in a different derived model. The second approach considers a “hybrid” model that extends the association model for 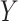 by incorporating causal as well as observational effects. The new approaches represent novel alternatives to the predominant approach that specifies effects of unobserved confounders, an approach that goes back to Cornfield and others (1959); see also Rosenbaum (2002).
by incorporating causal as well as observational effects. The new approaches represent novel alternatives to the predominant approach that specifies effects of unobserved confounders, an approach that goes back to Cornfield and others (1959); see also Rosenbaum (2002).
Following some background in Section 2, we present the new methods in Section 3. In Section 4, we jointly apply the two new methods to data from a study of parental factors in the development of dental caries among adolescents. A concluding discussion, including advantages and limitations of each method, is provided in Section 5.
2. Background
To demonstrate identifiability of natural direct and indirect effects, Imai and others (2010b) assumed the following, with 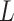 denoting a vector of baseline covariates (unaffected by
denoting a vector of baseline covariates (unaffected by 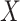 ):
):
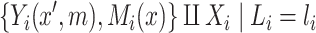 |
(2.1a) |
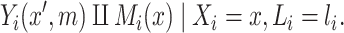 |
(2.1b) |
Assumption (2.1a) implies that the exposure 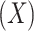 is random (or that exposure groups are exchangeable) conditional on
is random (or that exposure groups are exchangeable) conditional on 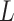 , while Assumption (2.1b) requires that there are no unobserved confounders (whether baseline or post exposure) of the
, while Assumption (2.1b) requires that there are no unobserved confounders (whether baseline or post exposure) of the 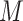 –
–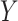 relationship conditioning on
relationship conditioning on 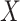 and
and 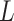 . The two assumptions together are referred to as “sequential ignorability”.
. The two assumptions together are referred to as “sequential ignorability”.
Imai and others (2010b) showed that under sequential ignorability (along with a standard consistency assumption),
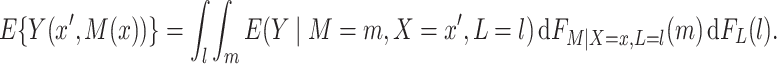 |
(2.2) |
The right hand side of (2.2) contains only association parameters and is thus estimable under appropriate association models for 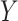 and
and 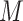 . Rather than integrate over an assumed distribution for
. Rather than integrate over an assumed distribution for 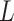 as indicated in (2.2), a convenient alternative approach is to sum over the empirical distribution of
as indicated in (2.2), a convenient alternative approach is to sum over the empirical distribution of 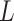 for the sample or other chosen reference group (e.g., subsample of exposed subjects). Equation (2.2), along with (1.1), yields estimable expressions for the natural direct and indirect effects. These expressions have been referred by Pearl (2012) as the mediation formula, although we tend to refer to Equation (2.2) itself as such.
for the sample or other chosen reference group (e.g., subsample of exposed subjects). Equation (2.2), along with (1.1), yields estimable expressions for the natural direct and indirect effects. These expressions have been referred by Pearl (2012) as the mediation formula, although we tend to refer to Equation (2.2) itself as such.
The assumption (2.1b) can be relaxed slightly for natural direct and indirect effects defined (as in (1.1)) in terms of expected potential outcomes (2.2). In particular, it suffices to assume an “independence in expectation” version of (2.1b). In the present paper, we consider an alternative assumption which also allows identification of the natural direct and indirect effects in combination with randomization of 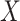 (2.1a). This assumption, which we refer to as “mediator comparability”, is written as,
(2.1a). This assumption, which we refer to as “mediator comparability”, is written as,
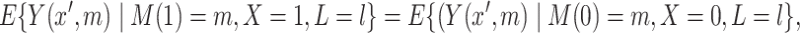 |
(2.3) |
for all 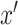 ,
, 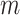 ,
, 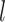 . This assumption says that the mean potential outcome of
. This assumption says that the mean potential outcome of 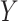 for a given exposure level
for a given exposure level 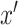 and mediator value
and mediator value 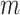 is the same for subgroups of the two observed exposure groups (
is the same for subgroups of the two observed exposure groups (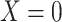 , 1) that are observed at a common level
, 1) that are observed at a common level 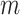 of the mediator (and covariate values,
of the mediator (and covariate values, 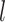 ), this holding for each
), this holding for each 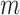 ,
, 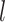 . As with sequential ignorability, the mediator comparability assumption is not testable from the data. Identifiability of natural direct and indirect effects using the mediator comparability assumption is shown in Appendix A of supplementary material available at Biostatistics online.
. As with sequential ignorability, the mediator comparability assumption is not testable from the data. Identifiability of natural direct and indirect effects using the mediator comparability assumption is shown in Appendix A of supplementary material available at Biostatistics online.
In a parametric approach to causal mediation analysis, the above potential outcome assumptions are used in conjunction with parametric association models for the outcome variables. For example, we will consider the following generalized structural equations model (GSEM),
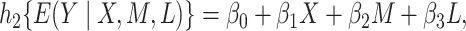 |
(2.4a) |
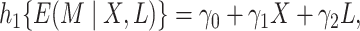 |
(2.4b) |
where 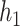 ,
, 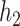 are invertible link functions, and the
are invertible link functions, and the 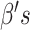 and
and 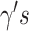 are unknown regression parameters, with
are unknown regression parameters, with 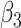 ,
, 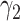 representing parameter vectors compatible with
representing parameter vectors compatible with 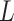 . In our approach to estimation, which is based on maximum likelihood, we need to further specify conditional distributions for each response variable
. In our approach to estimation, which is based on maximum likelihood, we need to further specify conditional distributions for each response variable 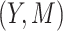 . We may also need to estimate non-regression parameters, for example, variances for normally distributed outcomes. In the present paper, we will assume response variables to follow exponential family distributions.
. We may also need to estimate non-regression parameters, for example, variances for normally distributed outcomes. In the present paper, we will assume response variables to follow exponential family distributions.
3. New sensitivity analysis methods
Our proposed methods, like that of Imai and others (2010b), assume randomization (or conditional exchangeability) of 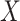 . The methods thus focus on the departure from the second sequential ignorability condition (i.e., (2.1b) or (2.3)), which is, roughly speaking, the assumption of no unobserved
. The methods thus focus on the departure from the second sequential ignorability condition (i.e., (2.1b) or (2.3)), which is, roughly speaking, the assumption of no unobserved 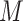 –
–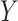 confounders. Further, also like Imai and others (2010b), these approaches assume that any
confounders. Further, also like Imai and others (2010b), these approaches assume that any 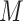 –
–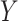 confounders are not affected by exposure. Note that such an effect would imply a causal model with a three-link path, thus departing from the present (two-link) mediation set-up. The former situation is considered by Imai and Yamamoto (2013) focusing on the linear model case; see also Albert and Nelson (2011) and Lange and others (2014).
confounders are not affected by exposure. Note that such an effect would imply a causal model with a three-link path, thus departing from the present (two-link) mediation set-up. The former situation is considered by Imai and Yamamoto (2013) focusing on the linear model case; see also Albert and Nelson (2011) and Lange and others (2014).
In addition, we note that while our focus is on the estimands 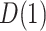 and
and 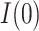 , the approaches for
, the approaches for 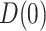 and
and 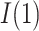 are completely analogous. The alternative versions of the direct and indirect effects are generally equal only in the case of a linear (identity link) model for
are completely analogous. The alternative versions of the direct and indirect effects are generally equal only in the case of a linear (identity link) model for 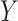 , and in the absence of an
, and in the absence of an 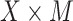 interaction. For other generalized linear models, they will tend to be very close (as in the case of our data example) when there is no interaction.
interaction. For other generalized linear models, they will tend to be very close (as in the case of our data example) when there is no interaction.
3.1. Copula model approach
The first approach uses a Gaussian copula model for the joint distribution of potential outcomes of 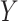 and
and 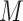 . Specifically, we suppose the existence of continuous latent variables,
. Specifically, we suppose the existence of continuous latent variables, 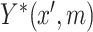 and
and 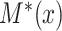 , corresponding to the (partially) observable potential outcomes,
, corresponding to the (partially) observable potential outcomes, 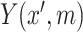 and
and 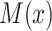 , respectively, for each
, respectively, for each 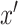 ,
, 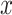 , and
, and 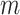 . We assume that
. We assume that 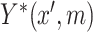 and
and 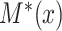 are bivariate normally distributed with correlation
are bivariate normally distributed with correlation 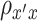 (assumed constant over
(assumed constant over 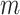 ) conditional on
) conditional on 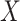 and
and 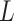 .
.
We make the standard consistency assumption that 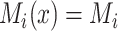 if
if 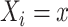 , and
, and 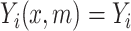 if
if 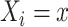 and
and 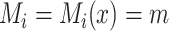 , where
, where 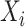 is the observed level of exposure
is the observed level of exposure 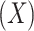 for individual
for individual 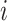 (similarly, for
(similarly, for 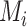 ,
, 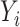 ). For discrete
). For discrete 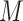 (taking values
(taking values 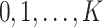 ), we further say that
), we further say that 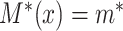 is “compatible” with
is “compatible” with 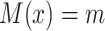 if
if 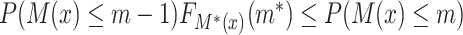 ,
, 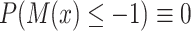 , where
, where 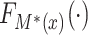 is the cumulative distribution function of
is the cumulative distribution function of 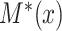 . From here on in, using the same symbol, one with an asterisk (the latent version), one without (the discrete, observed version), such as
. From here on in, using the same symbol, one with an asterisk (the latent version), one without (the discrete, observed version), such as 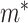 and
and 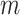 , will imply that the two values are compatible.
, will imply that the two values are compatible.
Given the assumed bivariate normal distribution for 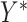 and
and 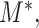 we have the regression relationship,
we have the regression relationship,
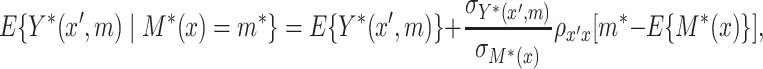 |
(3.1) |
where 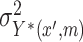 ,
, 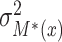 denote the variances of
denote the variances of 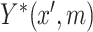 and
and 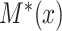 , respectively, all expectations (variances, and so on) in (3.1) being conditional on
, respectively, all expectations (variances, and so on) in (3.1) being conditional on 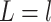 . From here on in, we will tend to leave conditioning on
. From here on in, we will tend to leave conditioning on 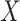 and
and 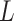 out of the notation unless needed for clarity; note that
out of the notation unless needed for clarity; note that 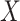 can be dropped anyway due to the assumption of randomized
can be dropped anyway due to the assumption of randomized 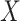 (2.1a). We will assume that
(2.1a). We will assume that 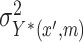 is constant over
is constant over 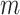 and write
and write 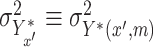 . We also write
. We also write 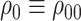 and
and 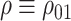 for brevity.
for brevity.
Our goal is the estimation of 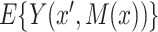 for all
for all 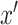 ,
, 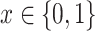 , which will allow estimation of the natural direct and indirect effects defined earlier. The case of
, which will allow estimation of the natural direct and indirect effects defined earlier. The case of 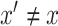 requires particular attention, and in fact is where the sequential ignorability assumption (i.e., (2.1b) or (2.3)) is ordinarily needed. For concreteness, and applicability to our data example, we focus on the estimand
requires particular attention, and in fact is where the sequential ignorability assumption (i.e., (2.1b) or (2.3)) is ordinarily needed. For concreteness, and applicability to our data example, we focus on the estimand 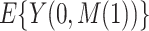 , needed for
, needed for 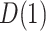 and
and 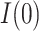 . The approach for the estimand
. The approach for the estimand 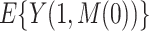 , which is involved in the expressions for
, which is involved in the expressions for 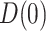 and
and 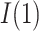 , is derived in a parallel manner by simply switching the values for
, is derived in a parallel manner by simply switching the values for 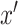 and
and 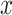 . We indicate maximum likelihood estimates (i.e., obtained under (2.4)) using the standard hat notation.
. We indicate maximum likelihood estimates (i.e., obtained under (2.4)) using the standard hat notation.
When 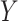 and
and 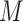 are continuous and assumed to be bivariate normally distributed then (3.1) holds for
are continuous and assumed to be bivariate normally distributed then (3.1) holds for 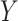 ,
, 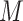 in place of
in place of 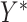 ,
, 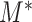 , and
, and 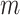 in place of
in place of 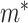 . In the special case where
. In the special case where 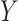 and
and 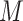 follow additive linear models (i.e., (2.4a,b) with identity link functions), it can then be shown that
follow additive linear models (i.e., (2.4a,b) with identity link functions), it can then be shown that 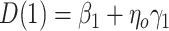 and
and 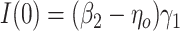 where
where 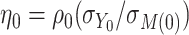 . Under homogeneous variance assumptions, allowing estimation of
. Under homogeneous variance assumptions, allowing estimation of 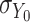 and
and 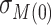 , the correlation parameter,
, the correlation parameter, 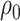 , may be used as the sensitivity parameter. The above and more general expressions for
, may be used as the sensitivity parameter. The above and more general expressions for 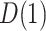 and
and 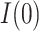 in the continuous
in the continuous 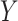 case are derived in Appendix B of supplementary material available at Biostatistics online.
case are derived in Appendix B of supplementary material available at Biostatistics online.
For discrete 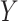 , we assume the regression relationship (3.1) for the latent final response variable
, we assume the regression relationship (3.1) for the latent final response variable 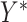 and mediator
and mediator 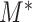 (also latent if
(also latent if 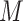 is discrete). In this case, constraining the marginal distribution of
is discrete). In this case, constraining the marginal distribution of 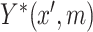 to be standard normal, the right side of (3.1) can be reduced to give,
to be standard normal, the right side of (3.1) can be reduced to give,
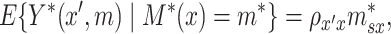 |
(3.2) |
where 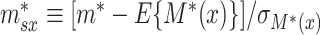 . Given our assumptions, we have
. Given our assumptions, we have 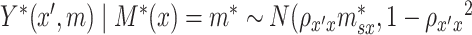 ).
).
We can then estimate 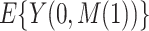 for given
for given 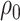 and
and  using Monte Carlo simulation. Here we present the algorithm for the case where
using Monte Carlo simulation. Here we present the algorithm for the case where 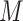 is continuous (and assumed normally distributed), in which case we use
is continuous (and assumed normally distributed), in which case we use 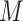 in place of
in place of 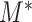 (and
(and 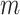 in place of
in place of 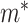 ) in the above expressions. Further details, including the case where
) in the above expressions. Further details, including the case where 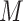 is discrete, are given in Appendix C of supplementary material available at Biostatistics online. The algorithm is implemented for selected values for
is discrete, are given in Appendix C of supplementary material available at Biostatistics online. The algorithm is implemented for selected values for 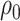 and
and 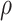 . For each person
. For each person 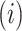 in the chosen reference group, do the following for replications
in the chosen reference group, do the following for replications 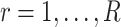 ,
,
Draw
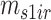 from
from 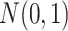 . Let
. Let 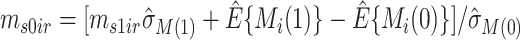 .
.Supposing the response for a given
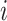 is
is 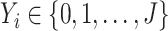 , let
, let 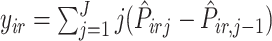 , where
, where 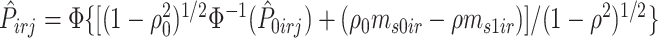 ,
, 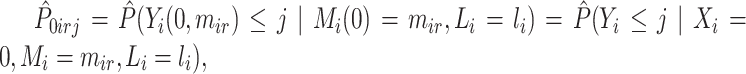 and
and 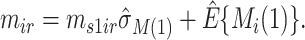
Then, compute 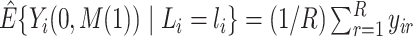 and
and 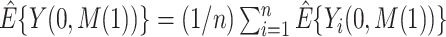 . Note that
. Note that 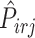 (in the second step above) represents the estimated conditional (cumulative) probability of
(in the second step above) represents the estimated conditional (cumulative) probability of 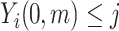 given
given 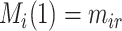 , and
, and 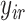 represents the estimated conditional expected value of
represents the estimated conditional expected value of 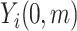 given
given 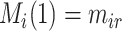 , both conditional on
, both conditional on 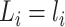 .
.
The natural direct and indirect effects, using the above estimated expected value, may be recomputed for varying values for 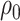 and
and 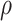 thus providing a sensitivity analysis. Confidence intervals for mediation effects for given
thus providing a sensitivity analysis. Confidence intervals for mediation effects for given 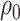 and
and 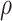 can be computed using the percentile bootstrap resampling method.
can be computed using the percentile bootstrap resampling method.
3.2. Hybrid model approach
In our second approach, we consider a hybrid causal-observational model for 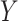 ,
,
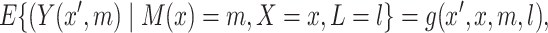 |
(3.3) |
where the right-hand side represents some specified parametric model. A key feature of this model is that it distinguishes different roles of the exposure, namely (i) a causal factor directly affecting 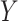 (denoted as
(denoted as 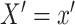 ) and (ii) the observed exposure group or cohort
) and (ii) the observed exposure group or cohort 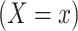 representing selection bias. It is possible to further generalize this model by distinguishing the exposure term in
representing selection bias. It is possible to further generalize this model by distinguishing the exposure term in 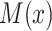 , but this will not be pursued here.
, but this will not be pursued here.
For our application, we consider the following additive hybrid model
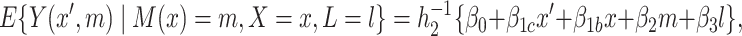 |
(3.4) |
where 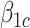 and
and 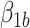 represent causal and cohort (selection bias) effects, respectively. Mediator comparability is obtained when the coefficients of all terms involving
represent causal and cohort (selection bias) effects, respectively. Mediator comparability is obtained when the coefficients of all terms involving 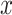 in the hybrid model (e.g.,
in the hybrid model (e.g., 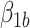 in (3.4)) are equal to 0. Note that the hybrid model (3.4) is distinct from previous causal models that may bear a resemblance to it, for example, Vansteelandt and others (2012) and Lange and others (2012). In the causal models in the latter papers, the dual exposure indicators both have a causal interpretation, as needed to define natural direct and indirect effects, whereas, in the hybrid model, they refer to different roles, i.e., causal versus observational, for the exposure variable.
in (3.4)) are equal to 0. Note that the hybrid model (3.4) is distinct from previous causal models that may bear a resemblance to it, for example, Vansteelandt and others (2012) and Lange and others (2012). In the causal models in the latter papers, the dual exposure indicators both have a causal interpretation, as needed to define natural direct and indirect effects, whereas, in the hybrid model, they refer to different roles, i.e., causal versus observational, for the exposure variable.
We also consider the following useful reparameterization of the hybrid model (3.4):
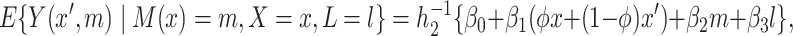 |
(3.5) |
where 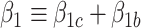 and
and 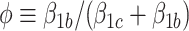 . As in model (2.4a),
. As in model (2.4a), 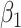 in (3.5) represents an association parameter, namely the effect of
in (3.5) represents an association parameter, namely the effect of 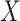 on
on 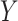 , conditional on
, conditional on 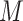 and
and 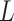 , on the scale corresponding to the link function,
, on the scale corresponding to the link function, 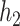 . The sensitivity parameter,
. The sensitivity parameter, 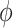 , represents the (nonidentifiable) proportion of the association effect due to the cohort effect, and, consequently,
, represents the (nonidentifiable) proportion of the association effect due to the cohort effect, and, consequently, 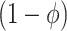 is the proportion of the association effect due to the causal effect of exposure. As the causal and cohort effects,
is the proportion of the association effect due to the causal effect of exposure. As the causal and cohort effects, 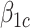 and
and  in (3.4), need not be in the same direction, it is possible for the “proportion”,
in (3.4), need not be in the same direction, it is possible for the “proportion”, 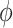 , to be negative or
, to be negative or 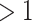 . Note that this reparameterization is only possible in the case of
. Note that this reparameterization is only possible in the case of 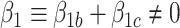 (i.e., a non-zero observed effect of exposure).
(i.e., a non-zero observed effect of exposure).
The case of 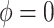 in model (3.5) implies that
in model (3.5) implies that 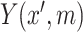 is (mean) independent of
is (mean) independent of 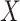 given
given 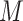 and
and 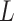 , and thus implies mediator comparability (2.3). In contrast,
, and thus implies mediator comparability (2.3). In contrast, 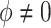 represents a departure from mediator comparability, and thus from sequential ignorability. Note that, as seen in (3.5),
represents a departure from mediator comparability, and thus from sequential ignorability. Note that, as seen in (3.5), 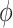 does not affect
does not affect 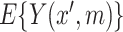 (nor, consequently,
(nor, consequently, 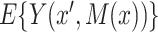 ) when
) when 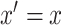 . This is as expected because then, under consistency,
. This is as expected because then, under consistency, 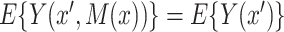 , which is estimable under randomization of
, which is estimable under randomization of 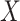 (2.1a), that is, without having to assume (2.1b) or (2.3). In Appendix D of supplementary material available at Biostatistics online, we provide a demonstration of the identifiability of the natural direct and indirect effects under the hybrid model with specified
(2.1a), that is, without having to assume (2.1b) or (2.3). In Appendix D of supplementary material available at Biostatistics online, we provide a demonstration of the identifiability of the natural direct and indirect effects under the hybrid model with specified 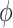 . The effect of departures from sequential ignorability on estimates (and percentile bootstrap confidence intervals) of the natural direct and indirect effects can thus be studied by varying
. The effect of departures from sequential ignorability on estimates (and percentile bootstrap confidence intervals) of the natural direct and indirect effects can thus be studied by varying 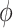 .
.
Some comments are in order on the specification of 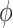 . The direct specification of
. The direct specification of  may be difficult as
may be difficult as 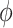 represents a measure of “collider-stratification bias” (see, e.g., Greenland, 2003) whose magnitude, and even direction, may be non-intuitive to many researchers. Fortunately, this bias, or an approximation, may be derived as a function of the effects of (possibly multiple) unobserved
represents a measure of “collider-stratification bias” (see, e.g., Greenland, 2003) whose magnitude, and even direction, may be non-intuitive to many researchers. Fortunately, this bias, or an approximation, may be derived as a function of the effects of (possibly multiple) unobserved 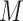 –
–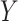 confounders on
confounders on 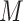 and
and 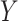 . Detailed guidelines for the elicitation of plausible values for
. Detailed guidelines for the elicitation of plausible values for 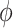 are provided in Appendix E of supplementary material available at Biostatistics online.
are provided in Appendix E of supplementary material available at Biostatistics online.
4. Application to dental data
We apply the two proposed sensitivity analysis methods to data from a dental caries study (Nelson and others, 2010). The study examined a cohort of very low birth weight (VLBW, with and without bronchopulmonary dysplasia, BPD) and a matched group of normal birth weight (NBW) children followed from birth through adolescence in an earlier study (Singer and others, 1997). This earlier study recorded parent information, including education, knowledge, and stress factors, from questionnaires given at the child's birth, ages 3 and 8. The children who continued on to the dental study underwent a dental clinical exam at around age 14. This exam provided, among other information, the number of decayed, missing, and filled teeth (DMFT) and the oral hygiene index score (OHI), an indicator of effective oral hygiene behavior.
Previous research considered the effect of mother education on child's dental outcomes at adolescence (Nelson and others, 2010). Nelson and others (2012) found that adolescents whose mothers had less than a high school education when the child was age 3 (compared with those whose mother had at least a high school education) had a higher mean DMFT. In the present paper, we seek to assess the extent to which this effect is mediated through OHI.
Our specific model variables included a binary exposure variable, “MomEd” (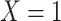 for mother's education at or below high school level, “low”, 0 otherwise, “high”), a binary final outcome, “DMFTD” (
for mother's education at or below high school level, “low”, 0 otherwise, “high”), a binary final outcome, “DMFTD” (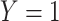 if the child had DMFT
if the child had DMFT 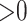 at the age 14 exam, 0, otherwise), and a roughly continuous mediator, OHI (ranging from 0 to 3, where higher is worse). We assumed that the model variables are causally related as indicated in the graph in Figure 1. In an initial mediation analysis, we assumed sequential ignorability controlling for the (child) variables: sex, race (African American versus other), and birth status (two indicator variables for the three categories: VLBW plus BPD, VLBW alone, and NBW).
at the age 14 exam, 0, otherwise), and a roughly continuous mediator, OHI (ranging from 0 to 3, where higher is worse). We assumed that the model variables are causally related as indicated in the graph in Figure 1. In an initial mediation analysis, we assumed sequential ignorability controlling for the (child) variables: sex, race (African American versus other), and birth status (two indicator variables for the three categories: VLBW plus BPD, VLBW alone, and NBW).
Fig. 1.

Mediation model for dental data (confounding variables not shown).
To describe the links in the mediation model, we assumed a special case of the GSEM (2.4a,b)) comprised of a logistic regression model for the binary outcome variable and a linear regression model for the continuous mediator as follows:
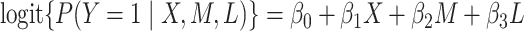 |
(4.1a) |
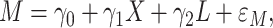 |
(4.1b) |
where 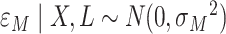 and
and 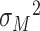 is an unknown variance parameter. As an alternative, we considered the above set of models but where (4.1a) is extended by adding an exposure by mediator (
is an unknown variance parameter. As an alternative, we considered the above set of models but where (4.1a) is extended by adding an exposure by mediator (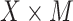 ) interaction term. The component models ((4.1a), without and with interaction, and (4.2b)) may be fit separately using standard likelihood methods. The estimated regression parameters for both the additive and interaction GSEM (the model for
) interaction term. The component models ((4.1a), without and with interaction, and (4.2b)) may be fit separately using standard likelihood methods. The estimated regression parameters for both the additive and interaction GSEM (the model for 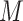 is the same in both cases) are given in Table 1.
is the same in both cases) are given in Table 1.
Table 1.
Parameter estimates(standard errors) from 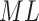 fit of model (4.1) of
fit of model (4.1) of 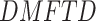 (without and with
(without and with 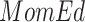 x
x 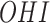 interaction) and
interaction) and 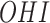 outcomes from dental data
outcomes from dental data
| DMFTD |
|||
|---|---|---|---|
| Covariates | Additive | Interaction | OHI |
| Intercept |
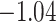 (0.45) (0.45) |
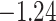 (0.52) (0.52) |
0.83 (0.15) |
| MomEd | 0.53 (0.33) | 0.92 (0.61) | 0.29 (0.12) |
| OHI | 0.66 (0.22) | 0.86 (0.35) | – |
MomEd 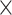 OHI OHI |
– |
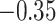 (0.44) (0.44) |
– |
| VLBW vs NBW | 0.21 (0.42) | 0.20 (0.43) |
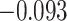 (0.15) (0.15) |
| BPD vs NBW |
 0.46 (0.39) 0.46 (0.39) |
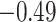 (0.39) (0.39) |
0.19 (0.14) |
| Race | 0.57 (0.33) | 0.55 (0.33) | 0.29 (0.12) |
| Sex |
 0.23 (0.33) 0.23 (0.33) |
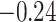 (0.34) (0.34) |
0.04 (0.12) |
For each GSEM, we then estimated the natural direct effect, 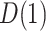 , and the natural indirect effect,
, and the natural indirect effect, 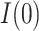 , using the mediation formula (2.2) plugging in parameter estimates obtained under model (4.1a,b) and using the VLBW subsample as the reference group. We present results from the additive model; results from the interaction model (not shown) are nearly the same, indicating that our mediation effect inferences are not changed substantially by inclusion of a MomEd by OHI (
, using the mediation formula (2.2) plugging in parameter estimates obtained under model (4.1a,b) and using the VLBW subsample as the reference group. We present results from the additive model; results from the interaction model (not shown) are nearly the same, indicating that our mediation effect inferences are not changed substantially by inclusion of a MomEd by OHI (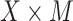 ) interaction effect in the DMFTD (
) interaction effect in the DMFTD (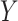 ) model.
) model.
Using the mediation formula under the assumption of sequential ignorability, we obtained an estimated natural direct effect (bootstrap 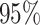 confidence interval) of
confidence interval) of 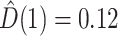 (
(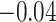 , 0.27), indicating that the probability of a DMFT would increase by an estimated 0.12 if MomEd (
, 0.27), indicating that the probability of a DMFT would increase by an estimated 0.12 if MomEd ( ) were changed from “high” to “low” but the OHI (
) were changed from “high” to “low” but the OHI ( ) fixed as if the mother had “low” education. The estimated natural indirect effect was
) fixed as if the mother had “low” education. The estimated natural indirect effect was 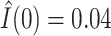 (0.01, 0.09), indicating that the probability of a DMFT would increase by an estimated 0.04 if MomEd was changed from “high” to “low” in a way that naturally affected OHI without affecting DMFTD through any other path. We also note that the estimated total effect (95
(0.01, 0.09), indicating that the probability of a DMFT would increase by an estimated 0.04 if MomEd was changed from “high” to “low” in a way that naturally affected OHI without affecting DMFTD through any other path. We also note that the estimated total effect (95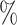 confidence interval) was
confidence interval) was 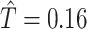 (0.003, 0.31) and the indirect effect (mediation) proportion an estimated 0.26. As indicated by the above confidence intervals, the indirect as well as the total (but not the direct) effect is statistically significant at the nominal 0.05
(0.003, 0.31) and the indirect effect (mediation) proportion an estimated 0.26. As indicated by the above confidence intervals, the indirect as well as the total (but not the direct) effect is statistically significant at the nominal 0.05 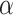 -level.
-level.
The above estimates and confidence intervals rely on the assumption of sequential ignorability (or (2.1a) and mediator comparability (2.3)). In the context of the dental data, mediator comparability implies that if set to a common exposure and mediator level, subgroups of the two observed exposure groups (with high versus low mother education) that are observed at a common observed mediator (oral hygiene index) level (and the same baseline control variable values) would have the same probability of dental caries. This assumption is unlikely for the dental data because there are apt to be unobserved confounders of the relationship between the oral hygiene index and dental caries. It is of interest to examine how the estimates of the natural direct and indirect effects would change under violations of the mediator comparability assumption.
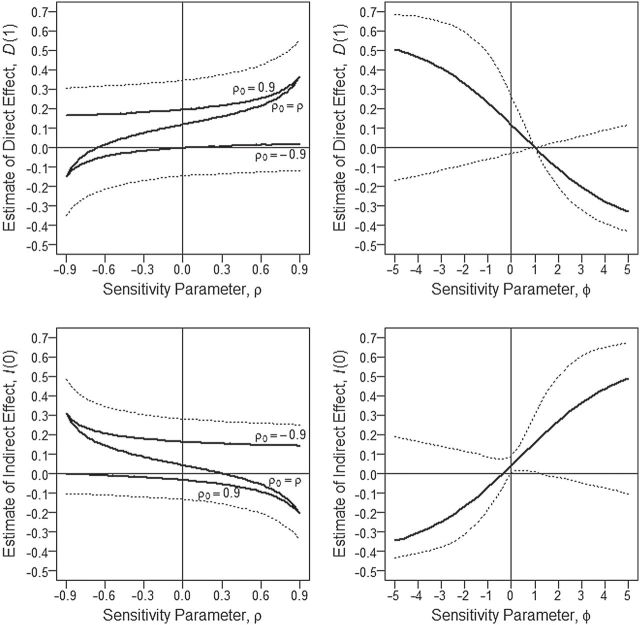
We conducted sensitivity analyses for the dental data using the two new approaches described in Section 3. The results of these analyses, including estimated (natural) direct and indirect effects and 95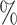 confidence intervals, are presented in Figure 2. Scientific considerations may allow us to narrow the range of plausible values for the sensitivity parameters, and thus obtain sharper conclusions about mediation effects. The elicitation of plausible sensitivity parameter values for the present data example is described in Appendix E of supplementary material available at Biostatistics online.
confidence intervals, are presented in Figure 2. Scientific considerations may allow us to narrow the range of plausible values for the sensitivity parameters, and thus obtain sharper conclusions about mediation effects. The elicitation of plausible sensitivity parameter values for the present data example is described in Appendix E of supplementary material available at Biostatistics online.
Fig. 2.
Sensitivity analysis for dental data. Maximum likelihood estimates of direct (top) and indirect (bottom) effects versus sensitivity parameters from copula model (left) and hybrid model (right). Solid 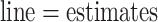 , dotted
, dotted 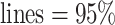 confidence interval bounds. For copula method, the upper bounds are for
confidence interval bounds. For copula method, the upper bounds are for 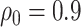 (direct),
(direct), 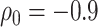 (indirect); the lower bounds are for
(indirect); the lower bounds are for 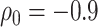 (direct),
(direct), 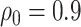 (indirect).
(indirect).
In the context of our data example, the hybrid model sensitivity parameter, 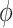 , is interpreted as the proportion of the association parameter,
, is interpreted as the proportion of the association parameter, 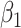 , that is due to selection bias, the remaining proportion being due to a true causal effect of MomEd. In the hybrid model (3.5), as in the corresponding association model (4.1a),
, that is due to selection bias, the remaining proportion being due to a true causal effect of MomEd. In the hybrid model (3.5), as in the corresponding association model (4.1a), 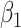 is interpreted as the log DMFTD odds ratio for low versus high MomEd groups conditional on OHI and the included baseline covariates.
is interpreted as the log DMFTD odds ratio for low versus high MomEd groups conditional on OHI and the included baseline covariates.
For the dental data, 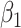 was estimated to be 0.53, providing an estimated odds ratio for low versus high MomEd of
was estimated to be 0.53, providing an estimated odds ratio for low versus high MomEd of 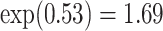 . Our elicitation suggested a range of plausible values for
. Our elicitation suggested a range of plausible values for 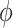 of
of 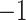 to 0, and a best (pessimistic) guess value of
to 0, and a best (pessimistic) guess value of 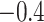 . The value of
. The value of 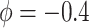 implies that the selection bias portion of the association effect is
implies that the selection bias portion of the association effect is 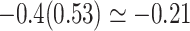 , while the portion due to the causal effect of MomEd on DMFTD is
, while the portion due to the causal effect of MomEd on DMFTD is 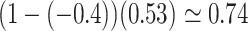 . Note that this decomposition can be expressed on the odds ratio scale:
. Note that this decomposition can be expressed on the odds ratio scale: 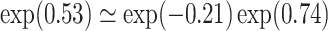 or
or 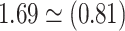 (2.09). For the copula model, our elicitation (Appendix E of supplementary material available at Biostatistics online) provided plausible (pessimistic) values of
(2.09). For the copula model, our elicitation (Appendix E of supplementary material available at Biostatistics online) provided plausible (pessimistic) values of 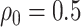 and
and 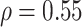 , and a plausible range for
, and a plausible range for 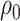 of [0.1, 0.7] and for
of [0.1, 0.7] and for 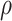 of [0.1, 0.75].
of [0.1, 0.75].
As indicated in the hybrid model curves in Figure 2, the elicited value of 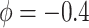 provides an estimate (95
provides an estimate (95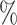 CI) for
CI) for 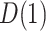 of 0.16 (
of 0.16 (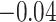 , 0.36) and an estimate (95
, 0.36) and an estimate (95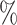 CI) for
CI) for 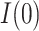 of
of 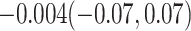 . The plausible range for
. The plausible range for 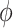 of [
of [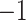 , 0] provides a range for the estimate of
, 0] provides a range for the estimate of 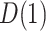 of 0.12 to 0.23 and for the estimate of
of 0.12 to 0.23 and for the estimate of 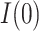 of
of 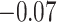 to 0.04. Figure 2 further shows that the 95
to 0.04. Figure 2 further shows that the 95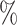 confidence intervals for
confidence intervals for 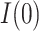 fail to exclude 0 for values of
fail to exclude 0 for values of 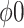 ; also, for
; also, for 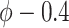 , the estimate for
, the estimate for 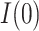 is no longer positive. For
is no longer positive. For 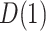 , neither the sign nor lack of statistical significance changes over the plausible range for
, neither the sign nor lack of statistical significance changes over the plausible range for 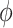 .
.
From the copula model, the pessimistic scenario of 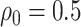 ,
, 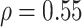 results in an estimate (95
results in an estimate (95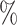 CI) for
CI) for 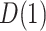 of 0.2 (0.05, 0.37) and for
of 0.2 (0.05, 0.37) and for 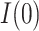 of
of 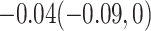 . As noted in Appendix E of supplementary material available at Biostatistics online, this scenario may be viewed as more pessimistic than the corresponding values obtained for the hybrid model. For the (lower bound) plausible values of
. As noted in Appendix E of supplementary material available at Biostatistics online, this scenario may be viewed as more pessimistic than the corresponding values obtained for the hybrid model. For the (lower bound) plausible values of 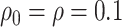 , we obtain an estimate (95
, we obtain an estimate (95 CI) for
CI) for 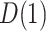 of 0.13 (
of 0.13 (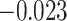 , 0.28) and for
, 0.28) and for 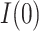 of 0.028 (
of 0.028 (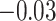 , 0.069). From these results, and as indicated in Figure 2, the estimate of
, 0.069). From these results, and as indicated in Figure 2, the estimate of 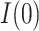 is no longer statistically significant (and goes from positive to negative) as
is no longer statistically significant (and goes from positive to negative) as 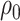 and
and 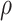 increase over their plausible ranges. Estimates for
increase over their plausible ranges. Estimates for 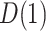 increase as the
increase as the 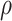 's increase and are statistically significant in part of the plausible range (as seen for the “pessimistic” scenario discussed above). These results are similar (apart from some differences in confidence interval coverage) to those obtained from the hybrid model approach.
's increase and are statistically significant in part of the plausible range (as seen for the “pessimistic” scenario discussed above). These results are similar (apart from some differences in confidence interval coverage) to those obtained from the hybrid model approach.
In regard to other features of the graphs, we note that the degenerate confidence interval at 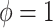 in the hybrid model approach is due to the fact that this value implies no natural direct effect of
in the hybrid model approach is due to the fact that this value implies no natural direct effect of 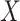 on
on 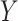 . Another difference between the two methods is that the confidence intervals from the copula model are generally more symmetric, reflecting the assumption of an underlying bivariate normal distribution for
. Another difference between the two methods is that the confidence intervals from the copula model are generally more symmetric, reflecting the assumption of an underlying bivariate normal distribution for 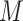 and
and 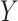 .
.
5. Discussion
We have presented two new approaches to sensitivity analysis for estimation of natural direct and indirect effects via the parametric mediation formula. Both approaches are flexible in allowing different variable types (i.e., discrete or continuous) for the outcome and mediator, each response variable following a generalized linear model. The approaches involve models (the copula and hybrid, respectively) providing particular departures from sequential ignorability, specifically (2.1b) or the mediator comparability assumption (2.3). Although our focus was on natural direct and indirect effects on a difference scale (as in (1.1)), because both sensitivity analysis methods provide estimates of expected potential outcomes, it would be straightforward to extend the method to inference on mediation effects defined on alternative scales, for example, relative risk or odds ratio for a binary 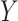 . Of course, the relationship between the sensitivity analysis parameters presented here and the mediation effects may be different depending on the scale used for the latter.
. Of course, the relationship between the sensitivity analysis parameters presented here and the mediation effects may be different depending on the scale used for the latter.
The two new sensitivity analysis methods have been encoded in SAS macros, which are available for downloading from http://epbiwww.case.edu/index.php/people/faculty/53-albert. These macros include alternative model and distributional options then those discussed in this paper. Additional examples, assuming normal and negative binomial distributions for 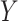 , are given in Appendix G of supplementary material available at Biostatistics online.
, are given in Appendix G of supplementary material available at Biostatistics online.
A difficulty of previous sensitivity analysis models that involve a hypothetical unobserved confounder is that the resulting model is generally incompatible with the model without the confounder (Lin and others, 1998). This problem is avoided in the proposed approaches as the corresponding sensitivity analysis models do not directly involve an unobserved confounder. Rather, in each of the new approaches the sensitivity analysis and association models are compatible by construction; for example, in the hybrid model the latter is obtained from the former when 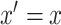 . However, unobserved confounders can be considered, and play a useful role, in the elicitation of plausible sensitivity parameter values for the proposed methods as described in Appendix E of supplementary material available at Biostatistics online.
. However, unobserved confounders can be considered, and play a useful role, in the elicitation of plausible sensitivity parameter values for the proposed methods as described in Appendix E of supplementary material available at Biostatistics online.
Between our two proposed methods, the copula model approach has an advantage of involving bounded (correlation) parameters. In addition, due to its underlying bivariate normal assumption and consequent linear structure, it appears to have more favorable inference properties, in particular, relatively narrow and symmetric confidence intervals across the range of sensitivity parameter values. The hybrid model approach, on the other hand, has the advantage of greater computational simplicity and a single sensitivity parameter (though more complex hybrid models, for example, involving an 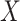 –
–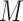 interaction, may be possible).
interaction, may be possible).
One way to reduce the sensitivity parameter dimensionality, and allow a simpler graphical presentation, for the copula model is to assume 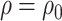 (analogously,
(analogously, 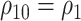 for the estimation of
for the estimation of 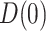 and
and  ). A more flexible approach would be to assume a functional relationship between the two correlation parameters, for example,
). A more flexible approach would be to assume a functional relationship between the two correlation parameters, for example, 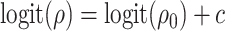 , where
, where 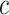 is a specified constant.
is a specified constant.
As elaborated in Appendix E of supplementary material available at Biostatistics online, carrying out both methods has the advantage that each can be used to calibrate and check the other. Although more work is needed in systematic approaches to combining sensitivity analyses, the present paper suggests the great potential for multiple models to provide a more refined and complete sensitivity analysis.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
Support for this research was provided in part by the National Institute of Dental and Craniofacial Research, National Institutes of Health (R01DE022674 to J.A.).
Supplementary Material
Acknowledgement
The authors thank the Associate Editor and referees for insightful and constructive comments that helped greatly in improving the paper. The authors also thank Cuiyu Geng for assistance in the construction of graphs and preparation of the paper, Dr Suchitra Nelson for helpful discussion and for providing data from her study of dental outcomes in VLBW and NBW children [NIDCR/NIH research grant number R21-DE16469], and Dr Lynn Singer for providing access to data from her cohort study of VLBW and NBW adolescents, supported by the Maternal and Child Health Program, Health Resources and Services Administration, Department of Health and Human Services (grant numbers MC-390592, MC-00127, and MC-00334). Conflict of Interest: None declared.
References
- Albert J. M. (2008). Mediation analysis via potential outcomes models. Statistics in Medicine 27, 1282–1304. [DOI] [PubMed] [Google Scholar]
- Albert J. M., Nelson S. (2011). Generalized causal mediation analysis. Biometrics 67, 1028–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baron R. M., Kenny D. A. (1986). The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology 51, 1173–1181. [DOI] [PubMed] [Google Scholar]
- Cornfield J., Haenszel W., Hammond E. C., Lilienfeld A. M., Shimkin M. B., Wynder E. L. (1959). Smoking and lung cancer: recent evidence and a discussion of some questions. Journal of the National Cancer Institute 22, 173–203. [PubMed] [Google Scholar]
- Greenland (2003). Quantifying biases in causal models: classical confounding vs. collider-stratification bias. Epidemiology 14, 300–306. [PubMed] [Google Scholar]
- Hafeman D. M. (2011). Confounding of indirect effects: a sensitivity analysis exploring the range of bias due to a cause common to both the mediator and the outcome. American Journal of Epidemiology 174, 710–717. [DOI] [PubMed] [Google Scholar]
- Imai K., Keele L., Tingley J. (2010a). A general approach to causal mediation analysis. Psychological Methods 15, 309–334. [DOI] [PubMed] [Google Scholar]
- Imai K., Keele L., Yamamoto T. (2010b). Identification, inference and sensitivity analysis for causal mediation effects. Statistical Science 25, 51–71. [Google Scholar]
- Imai K., Yamamoto T. (2013). Identification and sensitivity analysis for multiple causal mechanisms: revisiting evidence from framing experiments. Political Analysis 21, 141–171. [Google Scholar]
- Lange T., Rasmussen M., Thygesen L. C. (2014). Assessing natural direct and indirect effects through multiple pathways. American Journal of Epidemiology 179, 513–518. [DOI] [PubMed] [Google Scholar]
- Lange T., Vansteelandt S., Bekaert M. (2012). A simple unified approach for estimating natural direct and indirect effects. American Journal of Epidemiology 176, 190–195. [DOI] [PubMed] [Google Scholar]
- Lin D. Y., Psaty B. M., Kronmal R. A. (1998). Assessing the sensitivity of regression results to unmeasured confounders in observational studies. Biometrics 54, 948–963. [PubMed] [Google Scholar]
- Nelson S., Albert J. M., Lombardi G., Wishnek S., Asaad G., Kirchner H. L., Singer L. T. (2010). Dental caries and enamel defects in very low birth weight adolescents. Caries Research 44, 509–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson S., Lee W., Albert J. M., Singer L. T. (2012). Early maternal psychosocial factors are predictors for adolescent caries. Journal of Dental Research 44, 509–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl J. (2012). The causal mediation formula a guide to the assessment of pathways and mechanisms. Prevention Science 13, 426–436. [DOI] [PubMed] [Google Scholar]
- Robins J. M., Greenland S. (1992). Identifiability and exchangeability for direct and indirect effects. Epidemiology 3, 143–155. [DOI] [PubMed] [Google Scholar]
- Rosenbaum P. R. (2002). Observational Studies, 2nd edition New York: Springer-Verlag. [Google Scholar]
- Singer L. T., Yamashita T. S., Lilien L., Collin M., Baley J. (1997). A longitudinal study of infants with bronchopulmonary dysplasia and very low birthweight. Pediatrics 100, 987–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen E. J., Shpitser I. (2012). Semiparametric theory for causal mediation anlaysis: efficiency bounds, multiple robustness, and sensitivity analysis. Annals of Statistics 40, 1816–1845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T. J. (2010). Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology 21, 540–551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T. J., Chiba Y. (2014). Sensitivity analysis for direct and indirect effects in the presence of exposure-induced mediator-outcome confounders. Epidemiology, Biostatistics, and Public Health e9027-1–e9027-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S., Bekaert M., Lange T. (2012). Imputation strategies for the estimation of natural direct and indirect effects. Epidemiologic Methods 1(1), Article 7. [Google Scholar]
- Wang W., Albert J. M. (2012). Estimation of mediation effects for zero-inflated regression models. Statistics in Medicine 31, 3118–3132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W., Nelson S., Albert J. M. (2013). Estimation of causal mediation effects for a dichotomous outcome in multiple-mediator models using the mediation formula. Statistics in Medicine 32, 4211–4228. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.