Figure 1.

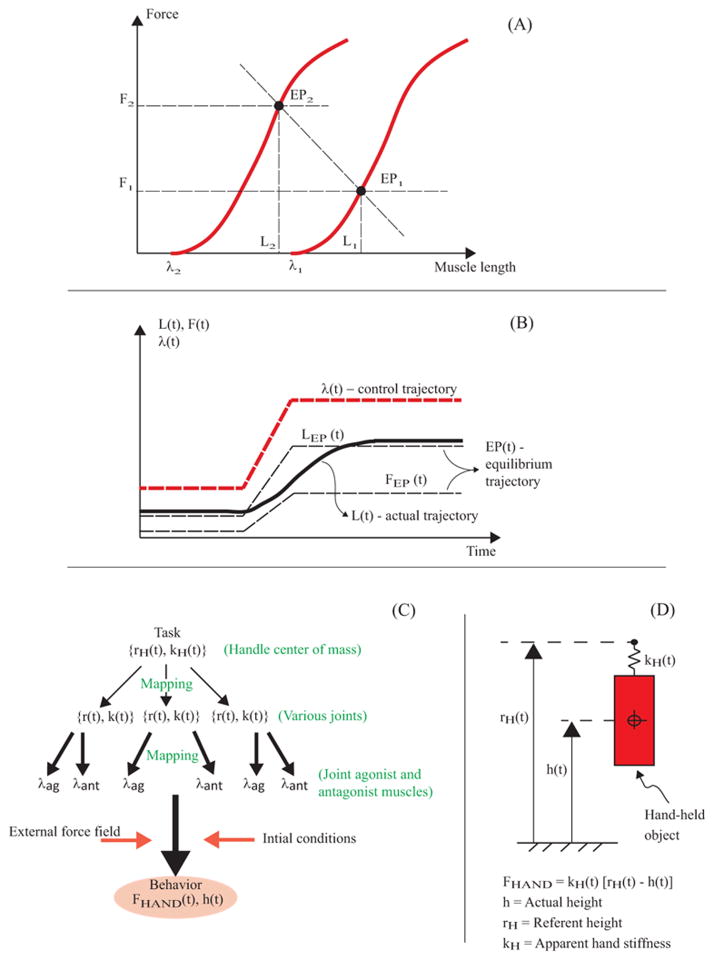
Panel (A) illustrates the dependence of active muscle force on muscle length (the bold curves) for two values of the threshold of the tonic stretch reflex (λ_i). For a given external load and given λ_i, an equilibrium point (EP_i) is achieved and is characterized by a specific muscle length and a specific force. A shift from λ₁ to λ₂ can lead to changes in both muscle length and force (a change from EP₁ to EP₂) depending on the external load characteristic. One such characteristic is illustrated in Panel (A). Panel (B) depicts the time profile λ(t), which is a control trajectory (bold, dashed line). It leads to changes in the equilibrium values of muscle length and force, L_EP(t) and F_EP(t). Taken together, these time functions comprise the equilibrium trajectory. Actual trajectory of muscle length and force (only L(t) is illustrated) depends on many factors such as the inertia of the moving system. Panel (C) depicts a scheme in which hypothetical central control commands (i.e., referent variables) are transformed into tonic-stretch-reflex thresholds for all the muscles involved in the action via a series of few-to-many mappings. Behavior, such as measured mechanical variables, emerges as a consequence of the central commands and external conditions. The object in Panel (D) experiences a force from the subject’s hand. As a first approximation, the hand force is modeled as a linear relation between the difference in the current, h(t), and referent, r_H(t), heights. The apparent hand stiffness, k_H(t), is the proportionality constant.