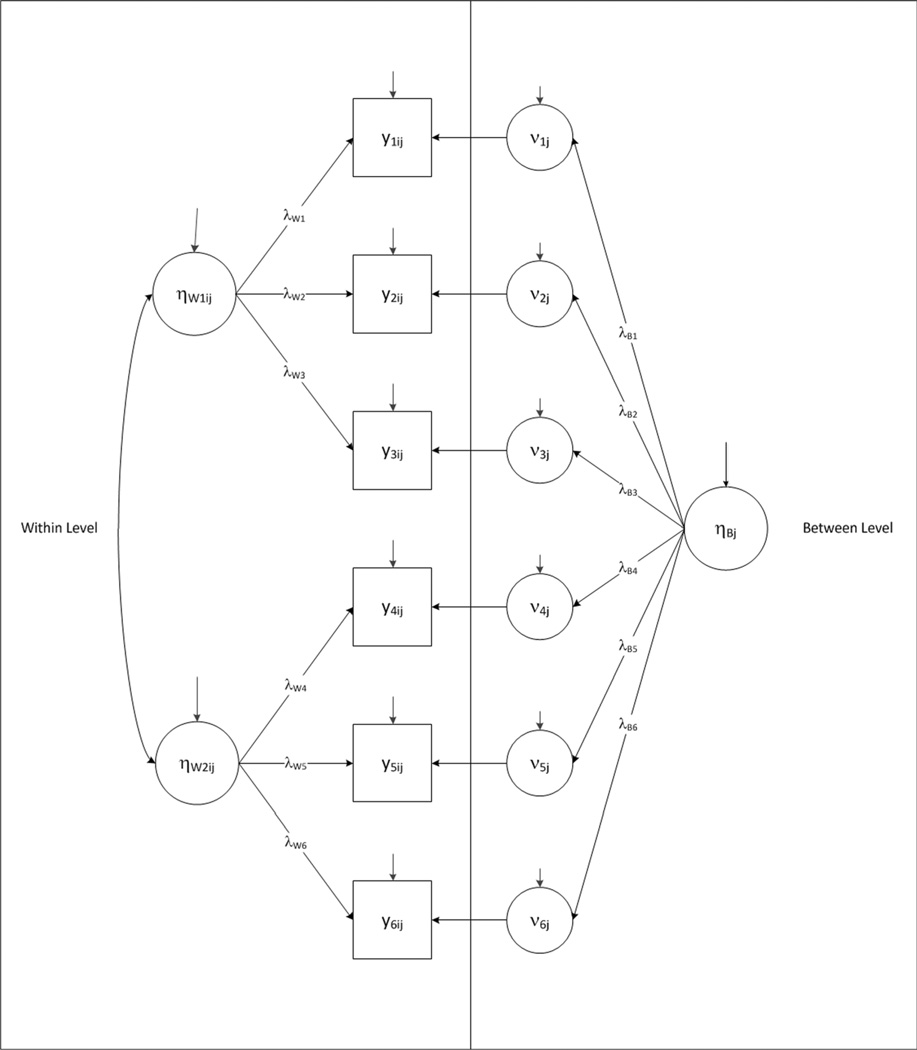
Fig. 1.

Multilevel factor analysis (MLFA). The components of a MLFA are illustrated above. This figure presents two separate measurement models—the within level (i.e., individuals within an environment) and the between level (i.e., between environments). At the within level, two individual-specific latent factors, η_W1ij and η_W2ij, influence the individual’s responses on six items (or observed variables) (y_1ij, y_2ij, …, y_6ij). At the between level, one school-specific latent factor,η_Bj, influences the school response means,ν_mj, that in turn influence the individual’s responses. The direction and size of the factor influences at each level are described by the λ_Ws and λ_Bs, respectively. Each item is measured imperfectly and thus has a residual indicated by the small vertical arrows in the diagram. The residual refers to the unique variance in the item not explained by or related to the latent factor; this unique variance is a combination of measurement error and other unique sources of variability