Figure 11.

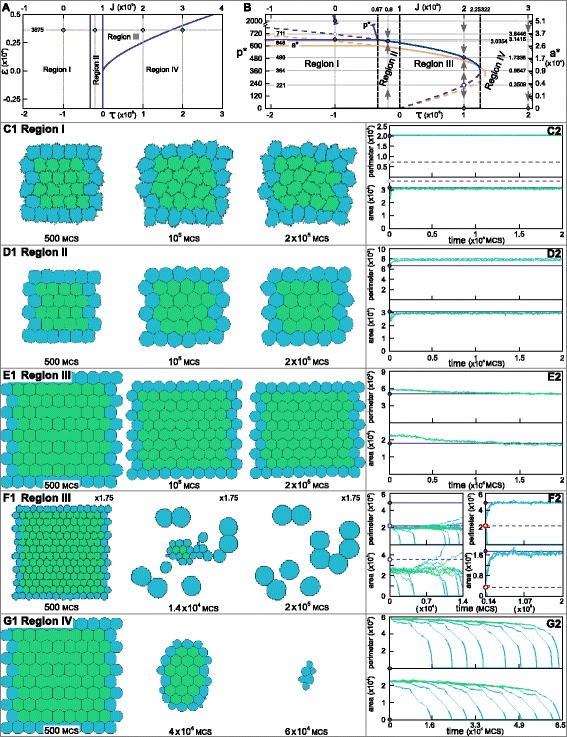
CPM simulations of epithelial packing within the four parameter regions.(A) Parameter settings at which the simulations are performed. In all simulations, ε=3,675. In regions I–IV, τ=−10⁵, −2·10⁴, 10⁵, and 2·10⁵, respectively. (B) Blue lines: Analytically derived bifurcation diagram of the cell dynamics, assuming hexagonal cell shape, as a function of τ (or equivalently J), with ε fixed at 3,675. Orange lines: corresponding bifurcation diagram for circular cell shape. Both equilibrium perimeter p ^∗ and area a ^∗ are shown. For J>67,011 cells take up a hexagonal shape, so p ^∗ and a ^∗ are trivially related; for J<67,011, p ^∗ and a ^∗ vary independently. Solid and dashed lines represent stable and unstable equilibria, respectively. Dots refer to the equilibria at simulation parameter settings, which can be stable (blue circles), unstable with respect to size (open circles), or unstable with respect to shape (open diamonds). The bifurcation points are indicated by black dashed lines. (Note the discontinuity in the p ^∗-axis.) (C1–G1) Snapshots of epithelial packing simulations in the different regions, as indicated. Initial cell size in (E1) was larger than the unstable equilibrium (p ^∗=221, a ^∗=3,509), whereas in (F1) it was smaller. All snapshots are displayed at the same scale, except for (F1), enlarged by a factor 1.75. Hexagonal cells, defined as cells with exactly six neighbours, are coloured green, all others light blue. (C2–G2) Time evolution of the perimeter (top) and area (bottom) of a subset of individual cells within the simulated epithelial tissue. Green and blue again indicate whether cells have six neighbours. Black solid lines indicate the analytically derived stable equilibria, dashed lines the unstable equilibria. Further parameter details are given in Appendix C.