Figure 3.

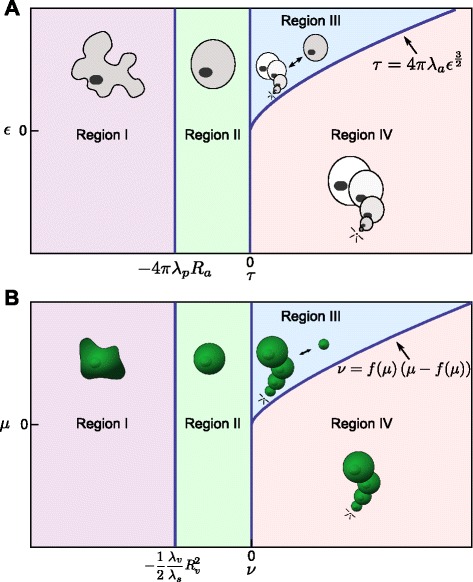
All possible dynamics for a 2D circular cell and a 3D spherical cell within the CSM formalisms can be captured by two aggregate biophysical parameters.(A) Bifurcation diagram showing the dynamics as a function of τ and ε. Region I (purple area): the interfacial tension is negative. The absence of positive tension along the membrane will lead to an unpredictable cell shape, at which a ^∗=A, and p ^∗=P−J/(2λ _p). Region II (green area): The cell has a positive interfacial tension at the equilibrium radius. However, when the radius is sufficiently smaller than the equilibrium radius, the interfacial tension is negative. Region III (blue area): a circular cell shape is always stable. There are two possible stable equilibria (bistable regime), a positive r ^∗=ρ ₁ and r ^∗=0, separated by an energy maximum at ρ ₂. Region IV (pink area): the only stable equilibrium is r ^∗=0, i.e. cells shrink and disappear. (B) Bifurcation diagram for a 3D spherical cell, plotted as a function of the aggregate parameters μ and ν. Qualitatively, the same four regions as obtained for the 2D case are observed for the spherical cell. Again, the cell behaviour is fully determined by two degrees of freedom, here shown for the (ν,μ)-space.