Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2015 May 12;8:8. doi: 10.1186/s13628-015-0022-x

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© Magno et al.; licensee BioMed Central. 2015

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.

PMC Copyright notice

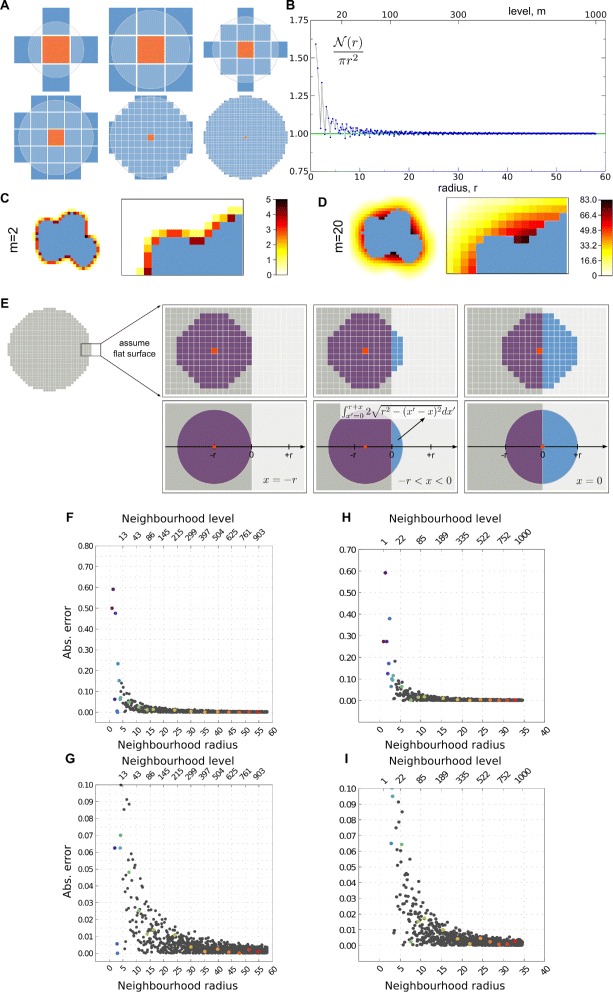
Perimeter determination in a lattice-based environment like CPM.(A) Examples of neighbourhoods. From left to right, top to bottom: von Neumann neighbourhood (m=1), Moore neighbourhood (m=2), third-, fourth-, twentieth- and hundredth-level neighbourhoods. Orange site indicates origin, neighbourhood (sites in blue) is determined by the neighbourhood radius (light blue circle). (B) Lattice points within a certain radius, relative to the expected area of a circle, as a function of neighbourhood radius. m indexes the corresponding neighbourhood levels. (C, D) Cell neighbouring regions used for perimeter-related computations in the CPM, for neighbourhood levels m=2(C) and m=20(D). Colour gradients denote the number of times neighbouring lattice points are taken into account in the perimeter computation. (E) The CPM cell perimeter in 2D (or surface area in 3D) is calculated by summing all lattice points falling within the given neighbourhood which have a different state (blue lattice points) than that of the cell (grey lattice points), for all lattice sites of the cell (red lattice points). The upper row illustrates the discrete process as is performed in a CPM simulation, while the lower row illustrates the continuous approximation of this process. (F–I) Precision of the CPM perimeter correction factor ξ depends on the neighbourhood level used in the CPM simulations. The graphs show the fractional difference between the numerical and analytical estimate of ξ as a function of the neighbourhood radius. (F, G) 2D numerical estimate compared with Eq. 29. (H, I) 3D numerical estimate compared with Eq. 33. For the numerical estimates a flat cell boundary is used with increasing neighbourhood levels, from 1 to 1,000. (G) and (I) are magnifications of (F) and (H), respectively.