Figure 2. Various dynamical behaviors of vaccine uptake emerge at different values of vaccine cost and efficacy in the rational decision model.

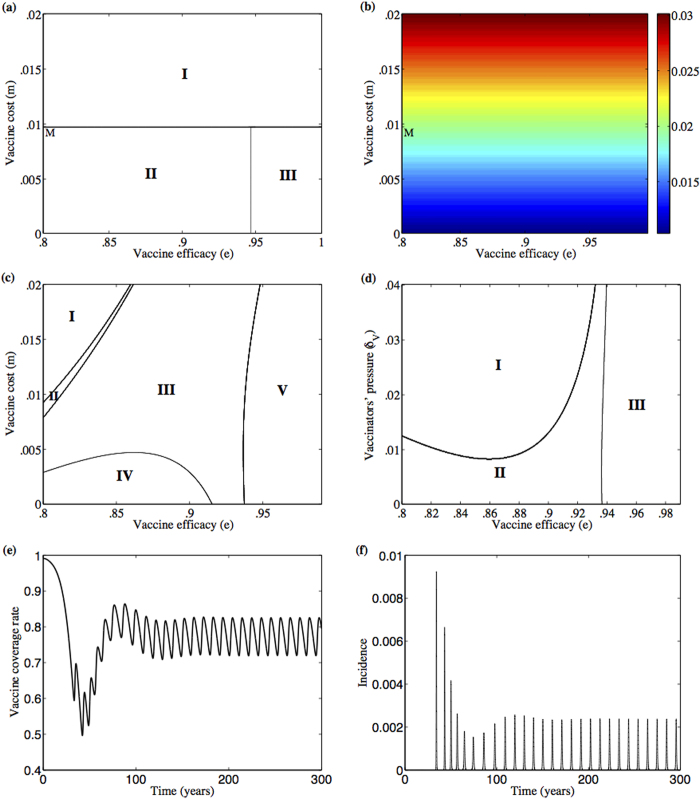
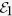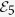(a,b) and the bounded-rationality model (c,d). e-m plane at δ_V = 0.02 of the rational decision model (a) and the bounded-rationality case (c,d) at cognitive parameters α_V = 0.8271, α_N = 0.9480, λ_V,o = 9.4515, λ_V,c = 1.7600, λ_N,o = 1.9011, λ_N,c = 1.7438, η_V = 0.2827, η_N = 0.5114. In (a) there are two bistability regions where the equilibrium points and are stable in region III, and the equilibrium points 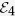and 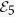are stable in region II. Besides, equilibrium point 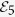is stable in region I and in an extremely narrow stripe between the two bistability regions II and III (bounded by e = 0.941159 and e = 0.941176). M = .00975 is the cutoff vaccine cost in case δ_V = 0.02 in (a) (see also panel (b)). (b) A contour plot for values of 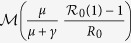calculated at each pair of (e,m) in the rational decision model. The full vaccination equilibrium point 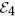is stable in the regions where δ_V is larger than the value of 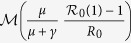and equation (8) in Appendix II is valid, that is e < 0.941159. With deviation from the rational decision model, a different e—m plane emerges in (c). There, a bistability region (II) of the equilibrium points 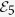and 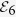transpires as well as other regions of stability for 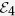in IV, 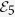in I, and 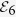in III. Limit cycles appear in region V. (d) e—δ_V plane of stability, at m = 0, in which the equilibrium point 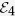is stable in region I and 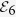in region II while limit cycles appear in region III. In both (c) and (d), the line between the regions where 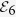is stable and the limit cycles is a supercritical Hopf bifurcation line whereas the rest of the lines are stability changing bifurcation lines. Limit cycles of vaccine coverage rate (e) and incidence (f) at δ_V = 0.02, m = 0, and e = 0.99. The rest of the parameters are κ = 1.69,c = 1.46,δ_N = 0.02 in all of the subpanels.