Figure 4.

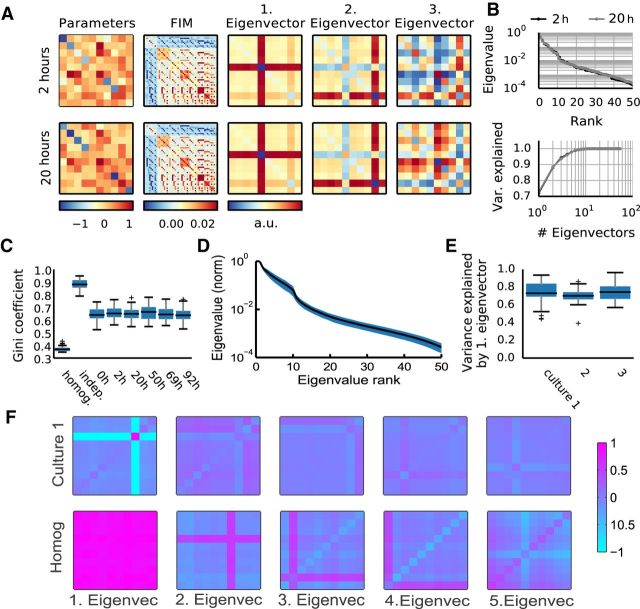
The FIM of maximum entropy models reveals a sloppy parameter space for neural activity. A, For each model (left; diagonal elements are local fields, upper triangle represents interactions, lower triangle filled to visualize that couplings between neurons are symmetric) the FIM is computed (second left). FIM is a 55 × 55 matrix, as there are 55 independent parameters in the model, 10 fields, and 45 symmetrical interactions. Next, the FIMs eigenvalues and eigenvectors are determined (middle to right; arrangement corresponding to the arrangement of parameters). This example shows the same group of neurons recorded 18 h apart (top vs bottom row). Although the parameters differ, the two FIMs and their first two eigenvectors are almost indistinguishable. For these two models, D_JS(M₁|M₂) ≈ 0.007, r_E² = 0.99 for the principal eigenvector and r_Λ² = 0.61 for the parameters. B, Eigenvalues of the example two models (top) and fraction of FIM variance explained by adding consecutive eigenvectors (bottom). C, Gini coefficients for the FIM computed for nonsparse Ising models (homogeneous; local fields and interactions both drawn from normal distributions with mean 0.14, and variance 1/10 of fitted fields and interactions), independent models (matching the firing rates of the data), and from six datasets recorded at different time points (same preparation as A). D, The shape of average eigenvalue distribution across groups in the first recording of Culture 1, with SD in blue. Note, log scale used for the eigenvalues; the disparity between eigenvalues and fast saturation of explained variance both suggest that the models are sloppy. E, FIM variance explained by the principal eigenvector across all groups in each of the cultures (first recording only, as it is representative). F, The first five eigenvectors (scaled by eigenvalues relative to the first) of a random group of neurons from Culture 1 (top row), against first five eigenvectors of a random group of neurons from the toy homogeneous model (bottom row).