Optimizing artificial neural network models for metabolomics and systems biology: an example using HPLC retention index data

Abstract

Background

Artificial Neural Networks (ANN) are extensively used to model ‘omics’ data. Different modeling methodologies and combinations of adjustable parameters influence model performance and complicate model optimization.

Methodology

We evaluated optimization of four ANN modeling parameters (learning rate annealing, stopping criteria, data split method, network architecture) using retention index (RI) data for 390 compounds. Models were assessed by independent validation (I-Val) using newly measured RI values for 1492 compounds.

Conclusion

The best model demonstrated an I-Val standard error of 55 RI units and was built using a Ward’s clustering data split and a minimally nonlinear network architecture. Use of validation statistics for stopping and final model selection resulted in better independent validation performance than the use of test set statistics.

Over the past decade the field of metabolomics has expanded to encompass applications in genetics, environmental sciences, human health and preclinical toxicity studies [1]. Metabolomics can be considered a pivotal component of systems biology where metabolite levels can be correlated with protein and gene expression data to provide a more inclusive understanding of living organisms. Recent improvements in MS and LC have enabled high-throughput detection of a large number of metabolites in biological samples. Likewise, improvements in chemometric tools have enabled the high-throughput extraction and comparison of raw data to determine which experimental features vary between sample groups. Unfortunately, the process of structure identification for observed features has remained time consuming, costly and frequently unsuccessful [2].

To address this dilemma, our group has undertaken development of MolFind/BioSM as an innovative approach for structural identification of chemical unknowns. MolFind/ BioSM uses the experimental exact mass of an unknown to search large databases and create a candidate list of possible matches. MolFind/BioSM applies five additional orthogonal filters to reduce the number of false positives returned from the exact mass search [2–6]. Filters are: HPLC retention index (RI) [3, 6–7], Ecom₅₀ [2,3] drift index (DI) [5], biological/nonbiological (BioSM) [8] and CID (MS/MS) spectra [5, 9]. In filtering, predicted values for RI, Ecom₅₀ and DI are made for candidate compounds using computational models. Candidates whose predicted values most closely match the experimental values of the unknown for RI, Ecom₅₀ and DI are returned as the most likely candidates. Surviving candidates are rank ordered based on results from the CID and BioSM models to create a final list. Filtering effectiveness is dependent on the computational models. For optimal performance, models should comply with the following: model data must have the correct structural diversity to apply to biochemical chemotypes; data must provide adequate coverage of the experimental data range; and the standard error of prediction (SE) must be as small as possible. MolFind/BioSM uses ± 3 SE filter ranges to filter out compounds whose predicted values are very different than the experimentally observed value of the unknown. Reductions in the SE lead to narrower filter ranges and the elimination of a greater number of false positives.

In previous studies [3, 6–7], RI was evaluated for the purpose of structure identification in the MolFind method. An HPLC-RI is generated using a homologous series of reference compounds with increasing lipophilicity. The RI value is a measure of relative (rather than absolute) retention time based on the reference compounds that elute just prior to and just after the solute of interest. Small changes in structure result in measurable changes in the retention index due to the ability of each atom to effect relative distribution between the mobile and stationary phases. Although many studies have been performed using ANN to model RI, [10–16] those studies have not addressed the issue of optimizing model development. Additionally, most studies were based on small datasets of homologous compounds and so do not address the issues of structure description inherent in modeling a diverse dataset. There are multiple algorithmic options and nearly limitless combinations of adjustable parameters to explore when constructing quantitative structure-retention relationships (QSRR) models with ANN learning methods. Thus, it is often difficult to establish best practices. Here we investigate ANN options by modeling RI data with a variety of learning parameters and testing the results with newly measured RI data and comparisons to a multiple linear regression (MLR) model.

Materials & experimental data

Experimental determination of retention index (RI) values

Reagents & standards

A mixture of retention index control compounds were prepared at 0.1 umol/ml in water:methanol (1:1). The purity of the C3–C6 index control compounds was as follows; n-propanamide 97%, n-butanamide >98%, n-hexanamide 98%. An equimolar mixture of n-heptanamide, n-octanamide, n-nonanamide, n-decanamde, n-undecanamide, n-dodecanamide, n-tridecanamide and n-tetradecanamide was synthesized by reacting a mixture of equimolar amounts of the respective n-alkyl carboxylic acids with ammonium carbonate. The identity of synthesized n-alkylamides was verified by accurate mass spectral analysis but purity was not determined. A methanolic mixture of C3-C6 n-alkylamides was combined with a methanolic mixture of the C7–C14 n-alkylamides and used as the retention reference calibration standard. Because of long term degradation that appeared to be caused by cross reactions between some of the control compounds, two separate stock solutions were prepared and mixed 1:1 for each analysis. Mixture A was composed of 0.2 umol/ml nicotinic Acid, N, N-dimethylbenzamide, corticosterone, probenecid, indomethacin, phenylbutazone, and thonzonium. Mixture B was composed of 0.2 umol/ml 2-aminopy-rimidine. Test compounds were used as received with no purification. Stock solutions of each compound were prepared at 1 mg/ml. Compounds with logP values ≤1 were dissolved in reagent grade water, compounds with logP values >1 and ≤2 were dissolved in reagent grade water:methanol (1:1) and compounds with logP values >2 were dissolved in methanol. Mixtures of ten compounds that differed in molecular mass by >±4 Da were mixed together at a concentration of 0.5 umol/ml along with a mixture of internal control compounds (0.16 umol/ml 2,3,3A,4,5,7,8,9,9A9B–Decahydro-3-hydroxy-3A–methyl-1H–benz(e)inden-7-one (S94) and 0.04 umol/ml mefenamic acid).

HPLC/MS system

Test compound mixtures were analyzed on an Agilent 1100 HPLC (Agilent, Santa Clara, CA, USA) system interfaced to a QTOF-2 mass spectrometer (Waters Associates, Beverly, MA, USA). The compounds were separated on a Zorbax SBC18 (1 mm × 150 mm, 3.5 um particle size) column containing a Zorbax Stable Bond (1 mm × 17 mm, 5 mm particle size) OptiGuard precolumn. Solvent A was 0.01% heptafluorobutryic acid (HFBA) in water and solvent B was 0.01% HFBA, 10% water in acetonitrile. The analysis was performed at a mobile phase flow rate of 75 ul/min using a linear solvent gradient from 0% solvent B to 100% solvent B in 17 min with a 5 min isocratic hold at 100% B. The column effluent entered the mass spectrometer electrospray source in positive ion mode. The source temperature was 120°C, the cone potential was 20 V and the capillary potential was 3.0 kV. The nitrogen nebulizer gas flow rate was 100 l/h, the cone gas flow rate was 50 l/h and the desolvation gas flow rate was 250 l/h at 120°C. To aid in efficient transfer of the ions through the collision cell the nitrogen collision gas was set at 12 psi and the collision energy was set at 10 eV. Full scan mass spectra were collected at 2 scans/s. HPLC chromatographic and mass spectral data were processed with Masslynx 4.0.

The development of a mobile phase for HPLC analysis of compounds with a wide range of polarities and hydrophobicities always involves compromises in optimizing chromatographic and detector efficiencies. Questions exist about the use of HFBA as an ion paring agent because of the potential for formation of HFBA cationic cluster complexes that may be detected as background ions or chromatographic peaks. To address this, LCMS data processing software has been adjusted to remove these ions from consideration. We believe that the retention of polar metabolites that would otherwise elute in the column void volume, and the decrease in both band dispersion and asymmetric elution of ionized basic compounds outweigh potential disadvantages.

Determination of test compound RI values

Prior to and at the end of each batch sample analysis 1 µl of a mixture of 1.4 umol/ml nitro-n-alkanes (C1-C10) and 1 µl of 0.7 umol/ml uracil were analyzed on the HPLC system using a diode array detector at 210 nm in place of the mass spectrometer. A batch HPLC/MS analysis consisted of the analysis of 1 µl of 1.4 umol/ml uracil, 1 µl of the control test mixture followed by 1 µl of each RI test compound mixture.

Conversion to n-amide RI reference standards

During the initial analysis of test compounds the retentions times were normalized relative to the retention times of a homologous series of nitro-n-alkanes. In previous studies we defined the RI value at the retention time of each nitro-n-alkane as 100 times the number of carbon atoms in the respective nitro-n-alkane reference compound. The RI values for each test compound were calculated from the derived fourth order polynomial equation of the nitro-n-alkane RI value versus the respective retention time. The nitro-n-alkane reference compounds have been a reliable retention reference, however they are undetectable by electrospray MS. In an effort to develop a homologous series of retention reference compounds that could be detected by positive ion electrospray, we investigated the use of the n-alkylamide (C3-C14) series of compounds. For this study, RI values were calculated relative to the nitro-n-alkanes, but the RI values for the nitro-n-alkane homologues series was defined relative to the retention of the n-alkylamides in the HPLC system. The new RI values (RIamide) are based on equating 100 times the number of carbon atoms in the respective n-alkylamide to their respective retention times. Since the relationship of the RIamide values of the reference compounds relative to their retention times was linear, the RIamide values of the test compounds were calculated by linear interpolation between the retention times of the reference compounds that eluted before and after the respective test compound.

Dataset structural profile

The measurements described above resulted in RI values for 390 structurally diverse compounds. Examples of more than 40 different hydrophilic functional groups are present including amine, aniline, pyridine, pyrrole, ether, ester, ketone, alcohol, carboxylic acid, phenol and amide. In addition, there are numerous related functional subgroups such as the ‘amide-like’ features that contain an amide and an extended conjugated system of oxygen, nitrogen and carbon atoms. Examples of amide-like features include urea, imide, guanine, xanthine, cytosine, uracil, barbiturate, uric acid, hydantoin, pyrazolidinone and flavin. Limited examples of aldehyde, diazole, purine, guanidine, pyrimidine, guanine, xanthine, pyrazolidinone, phosphate, phosphonate, sulfonic acid, sulfinic acid, thioether, thioanisole, disulfide, sulfoxide, quaternary nitrogen and pyridinium are present. Hydrophilic functional groups appear in numerous combinations ranging from one group to six. Numerous lipophilic skeletal features are also present including vinyl, phenyl, napthyl, cyclopentyl, cyclohexyl, t-butyl and a variety of chain lengths and branching patterns. Molecular weight ranges from 79 to 609 Da with an average of 217 Da. Structures for all compounds are given in Supplementary information [SI1].

Methods: model data

Model generation overview

Creation of a quantitative model is a process involving the acquisition of data and multiple data processing steps. A model is built on data consisting of a group of molecular structures and a corresponding group of experimentally measured endpoints (targets). In order to facilitate processing by machine learning algorithms, structures are reduced to numerical descriptors that encode structural characteristics from which variation in the target arises. The structures reduced to descriptors and the target values together constitute the model dataset. The target and structure descriptors values may need to be normalized and scaled to comply with algorithm input requirements. The dataset must also be partitioned into subsets. Some data are used for learning (training set), some data are used to determine when to stop learning (test set), and some data are withheld for validation (validation set). The dataset partitioned into train/test/validate subgroups is referred to as a data split. Finally, the subdivided data must be processed by an appropriate learning algorithm to enumerate the relationship between the descriptor values and the target. The quality of the resulting relationship is characterized by statistics tabulated for the subsets of the data split. The model dataset was described in the Materials & experimental data section. The descriptors, input normalization and scaling, and data partitioning methods are discussed in the remainder of this section.

Structure descriptors

A set of 36 structure information representation descriptors (SIR) [17–22] was selected to form the basis of an HPLC-RI QSRR model. Descriptors values were calculated using winMolconn, v2.1 (Hall Associates Consulting, Quincy, MA, USA). Molconn descriptors do not require a specific three-dimensional geometry to be determined for each structure. This is important given the throughput required by the MolFind/BioSM method. Descriptors were chosen to explicitly describe every feature of every molecule that would likely influence retention time.

Feature descriptors

Feature descriptors encode information about parts of a molecule (rings, atom types, functional groups, etc.). Challenges exist when selecting feature descriptors for a dataset that is diverse compared with its size. Diverse datasets require numerous inputs to encode all relevant chemical information and statistical constraints on the number of inputs relative to the number of data rows make it difficult to encode sufficient structure information in a statistically acceptable number of inputs.

The Interaction Group E-State (IGroup) descriptors were used to address this issue. The IGroups methodology [7] explicitly represents every atom in a molecule by grouping atom level contributions from atoms that undergo similar noncovalent interactions in solution. Atom level contributions are quantified by the Atom-level Electrotopological State (E-State) [19]. The E-State quantifies the electron accessibility at each atom as the buildup or depletion of valence electron density modified by the topographic accessibility. The E-State is a measure of the extent to which the atom will participate in noncovalent intermolecular interactions. IGroups are created by assigning atoms from related functional groups to a unified set of descriptors. The amide-like features described earlier are an example of an IGroup. Other IGroups include acids (carboxylate, phosphate, phosphonate, sulfonate, sulfiniate), anilines (aniline, benzamidine), aromatic nitrogen (pyridine, quinoline, pyrimidine), permanent charge nitrogen (quaternary nitrogen, pyridinium) and others. After atoms are assigned to an IGroup, a discrete index is created for each noncarbon atom-type in the group. Each discrete index is created from the sum of the atom-level E-State values for all atoms in the molecule in the IGroup category. The IGroups method allows for the description of complex series of related functional groups in a small number of indices.

Graph-based and molecular connectivity feature descriptors were selected to encode feature information about branching, rings and flexibility including number of rings, number of circuits, number of rotatable bonds, the chi simple path-cluster 4 index, and the chi simple chain 5, 6 and 7 indices [21]. Finally, an E-State based internal hydrogen bonding index was used to encode the strength of molecular subgraphs that are likely to form internal hydrogen bonds.

Global descriptors

Global descriptors encode information that is common to all compounds. For this study, chi valence 0 [21] was used to approximate molecular volume. Two global indices were used to characterize hydrophilicity and lipophilicity. The rvalHyd index (ratio valence hydrophilic index) [3] is the sum of atom level E-State values of hydrophilic atoms divided by the sum of atom level E-State values for every atom in the molecule. This index quantifies the proportion of valence electron density associated with hydrophilic atoms. The sumLip [3] index (total lipophilic E-State) is the sum of the atom level E-State value for all lipophilic atoms in the molecule. Two global shape descriptors were created for this project. These descriptors are flatness, and inverted difference simple chi 2 (inv_dx2). The flatness index gives the ratio of the number of sp2, sp and aromatic atoms to the total number of atoms. The inv_dx2 index was created by subtracting the simple difference chi path 2 (dx2) index value for the molecule from 10. Since dx2 is 0.0 for molecules with no branching, straight chain molecules have an inv_dx2 value of 10 and inv_dx2 gets smaller with branching and rings. Formal definitions for all descriptors are given in Supplementary Information [SI2].

Input normalization & scaling

Neural nets models created in the study utilize a sigmoid transfer function that requires inputs with values from 0.0 to 1.0. To satisfy these constraints, descriptor values were normalized by Z-score and then scaled. For feature descriptors, a value of 0.0 indicates the feature is absent. For this reason, normalization of feature inputs used the mean and standard deviation of the nonzero rows. Feature descriptors values of 0.0 were not normalized or scaled to preserve their null-set significance. Because global descriptors have a meaningful value for every compound, global inputs were normalized using the mean and standard deviation for all rows.

Following normalization, normalized values of global descriptor were scaled from 0.1 to 0.7. The 0.7 maximum leaves ‘headroom’ to allow the model to make predictions for compounds with input values larger than those in the training data. For feature descriptors with nonzero values, normal values were also scaled from 0.1 to 0.7. Global descriptors for flatness and inv_dx2 were scaled from 0 to 1 because both have a theoretical minimum and maximum that cannot be exceeded, regardless of the molecule being described.

Dataset partitioning

The 390 compound dataset was partitioned into a train/test/validate data split as described above. Certain aspects of the data splitting process require examination at this point.

Random data split

In many previous ANN studies, the data split was created with random assignments. There are potential problems associated with this method [23]. ANN learning occurs by downward navigation on an n-dimensional error surface. Since the error surface is a function of the input descriptor values and the error (difference between target and predicted values), it is possible that a random split can introduce bias into the error surface and thus the learning process. Bias can be related to the target values, structure descriptor values, or both. This is especially true with datasets that are sparsely clustered in target property or descriptor space. When clusters of data are small and widely separated, there is an increased chance that a random split could place too many similar compounds into the training or validation set. This could result in a training space and corresponding error surface that does not effectively discriminate structure and property space. If too many compounds of a given class with small target values are randomly assigned to the validate set, the training set could lack the necessary information to discriminate between large and small target values for compounds of that class. All compounds of the class would tend to be overpredicted because most similar training set compounds have large target values. Since models predict best when interpolating a solution, it is optimal for the training space to have as large a numerical range as possible in both structure parameters and target property values. It is impossible to predict the range that will result from random assignments.

When multiple random splits of the same data are modeled, there can be significant variation in the compounds with the worst predicted residuals. Thus, poor predictions can arise solely from the data split composition. Since the goal of a model is to make as many good predictions as possible, the question arises as to whether there is an optimum method of creating a data split.

Deterministic data split

For the initial model optimizations investigated, a deterministically constructed data split was used to reduce the risk of bias. Other data splitting methods are evaluated in later sections. A deterministic [23] split is constructed to balance the structural diversity and experimental target range across the split subgroups. For this reason, a deterministic data split method must have a means to quantify both the structure and target spaces of available data. A deterministic data split was constructed using the following method.

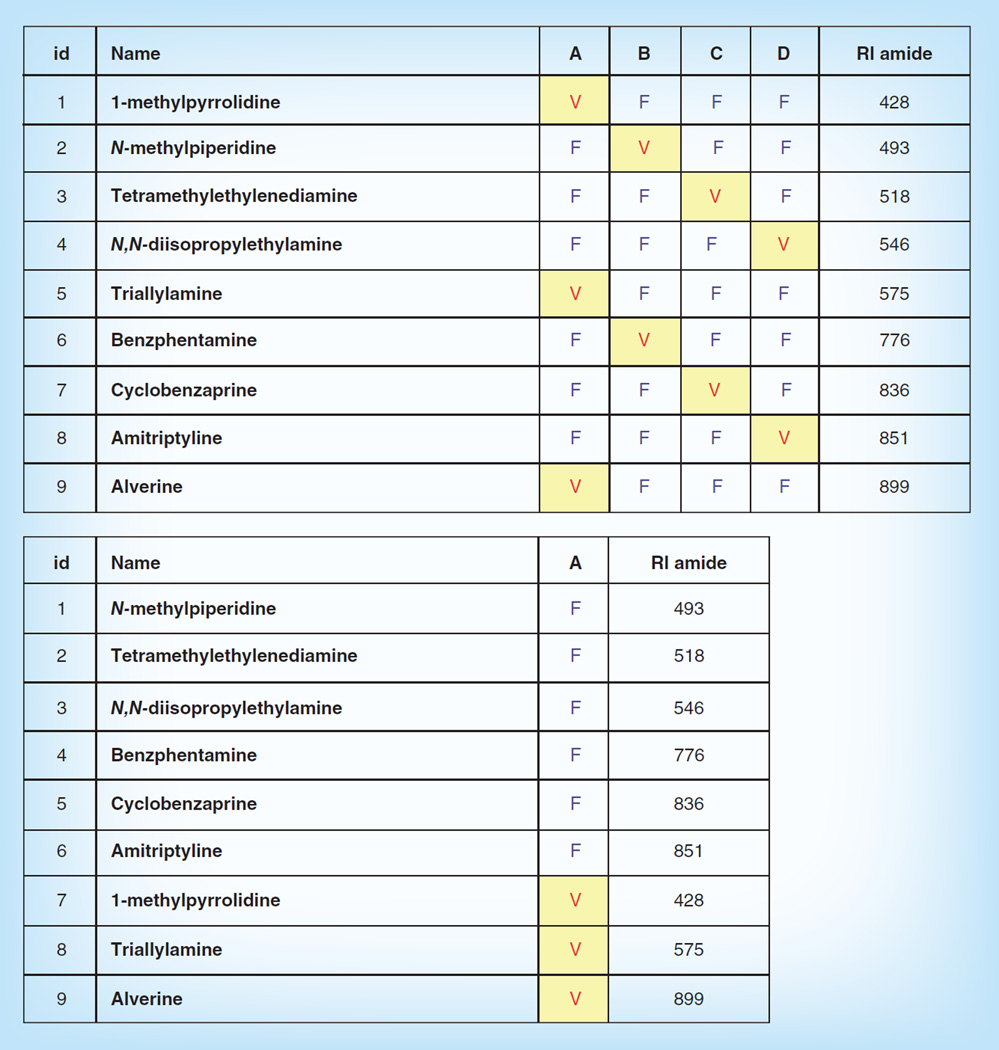
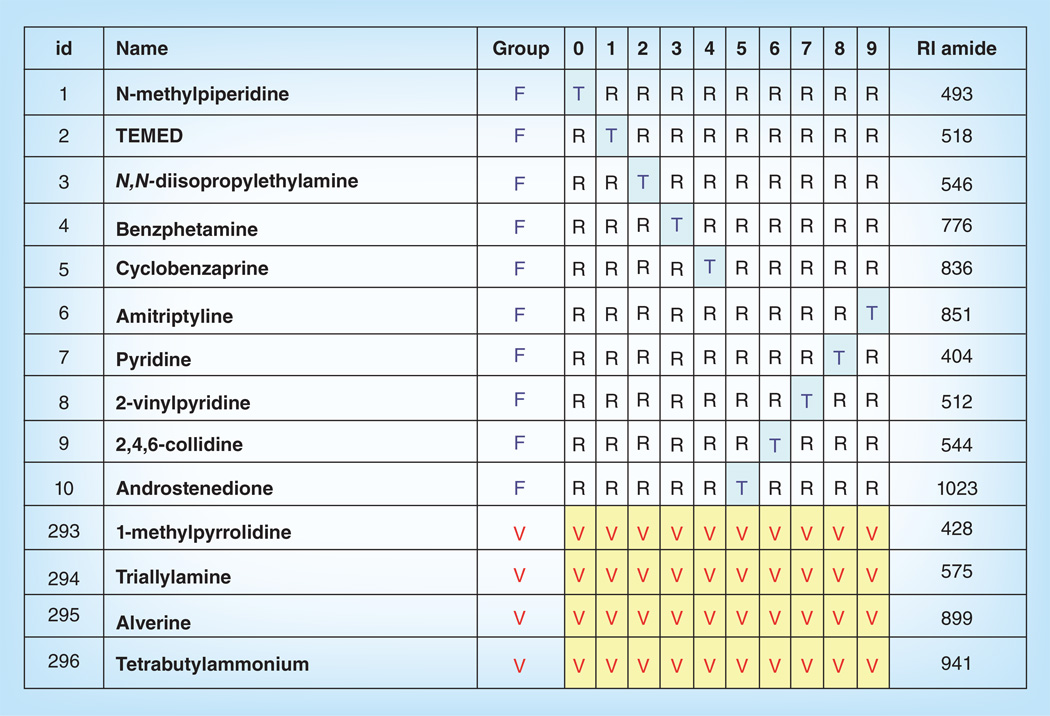
Model descriptors described earlier include 18 IGroups to encode heteroatomic functional groups. A bitkey of 18 bits was constructed for each compound with one ‘on-bit’ for each IGroup descriptor with a nonzero value. A bitkey is a string of bits with each bit representing one feature. A bit is ‘on’ (1) if the feature is present and ‘off’ (0) if the feature is absent. Compounds were sorted on bitkey value to identify groups of compounds with the same heteroatomic features. Compounds were rank ordered on experimental RI within each bitkey group. Groups were given an overall order from simple to complex with one on-bit compounds coming first. All groups of compounds with 1 on-bit were further sorted so that the 1 on-bit group with the largest number of members was placed first, followed by smaller groups in descending order. This procedure was repeated for groups with 2 on-bits, up to the maximum observed 12 on-bits.

After the bitkey order was established, data were partitioned into train, test and validate sets using the 4 × 10 × 10 ensemble method published previously [2–3,7]. To create the data split, available data were divided into four fit/validate sets (A,B,C,D). In each set, 25% of the data were assigned to validate and 75% were assigned to the fit set. Each compound was assigned to exactly one validate set. Because the data were preordered on bitkey and RI values, fit/validate sets were constructed by assigning every fourth compound to validate. After assignment, the rows of each set were reordered placing the validate rows last. After the fit/validate sets were created, each fit set was further subdivided into tenfolds. In each fold, 90% of the data were assigned to the training set and 10% were assigned to the test set. The test set for each fold was created by assigning every tenth compound to test. Each fold begins assignment on a different row so each compound is assigned to the test set in exactly onefold.

Assignment by the above method insures that a relatively equivalent number of structures from each structural subgroup were assigned to train, test and validate. The secondary ordering on RI value helps to insure an even distribution in target space. The result is that each fit/validate set has been subdivided into tenfolds, each with its own test set. Additionally, 25% of the data have been withheld for validation. Since the data split contains four fit/validate sets, validation data were available for every compound. The final ensemble was comprised of 40 models where each compound is in the training set of 27 models, the test set of 3 models and the validate set of 10 models. This process is illustrated in Figure 1.

Figure 1. Bitkey split assignment of validate rows and test set assignment for fit/validate set A.

The top figure shows nine compounds in a bitkey group rank-ordered on RI. To create four fit/validate sets, every fourth compound is assigned to validate. Set B assignment starts with the second row, set C the third row, etc, so that each compound is assigned to exactly one validate set. The middle figure shows fit/validate set A reordered with validate compounds last. The bottom figure shows some compounds in fit/validate set A with validate rows (V) moved to the end. The fit rows (F) for fit/validate set A are partitioned into ten train/test folds (0–9) by assigning every tenth compound to the test set (T). The result is 40 unique folds of the data. Every compound is used for training in 27 folds, for testing in threefolds, and for validation in tenfolds. A separate model was built for each fold. The top figure shows nine compounds in a bitkey group rank-ordered on RI. To create four fit/validate sets, every fourth compound is assigned to validate. Set B assignment starts with the second row, set C the third row, etc, so that each compound is assigned to exactly one validate set. The middle figure shows fit/validate set A reordered with validate compounds last. The bottom figure shows some compounds in fit/validate set A with validate rows (V) moved to the end. The fit rows (F) for fit/validate set A are partitioned into ten train/test folds (0–9) by assigning every tenth compound to the test set (T). The result is 40 unique folds of the data. Every compound is used for training in 27 folds, for testing in threefolds, and for validation in tenfolds. A separate model was built for each fold.

The data split described above was used to build an MLR model and multiple ANN models in an optimization process. Because optimization is a series of dependent steps where each successive optimization is dependent on the results of the previous step, ANN optimization results are presented incrementally in the methods section following the description of each optimization procedure. ANN optimizations are compared with an MLR model, so MLR modeling results are presented in the next section. Summary results are also given in the results section.

Methods: MLR model & ANN background

Baseline MLR model

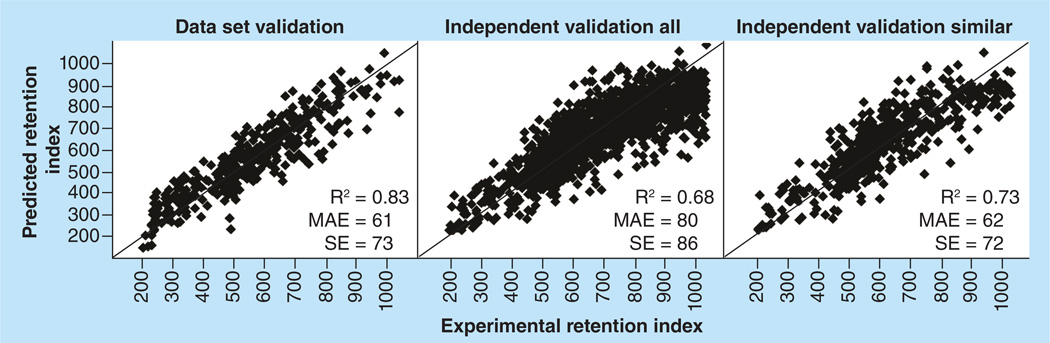
As a starting point, a multiple linear regression (MLR) model of the bitkey data split was created using JMP version 4.2 (SAS Institute Inc., Cary, NC, USA). A separate MLR was created for each of the four fit/validate sets. The fit set data were used to create a model that was evaluated with predictions of the validation data. MLR modeling resulted in a validation set r² of 0.83, mean absolute error (MAE) of 61 RIU and standard error (SE) of 73 (Figure 2). Performance was less good when predicting new data. An average prediction from all four models was used for independent validation (IVal) using 1492 compounds for which RI was recently measured. Results were r² = 0.68, MAE = 80 and SE = 86. When the model applicability domain was accounted for, results for compounds similar to model data were r² = 0.73, MAE = 72 and SE = 83 (Figure 2). Since the requirement of MolFind/BioSM is a model with the smallest possible ±3 standard error filter range, an ANN solution was investigated to determine if IVal results could be improved. ANN was chosen because neural networks have been used to create a successful model [2–3,7] of similar data based on N-nitro alkane standards.

Figure 2. Multiple linear regression model dataset validation results and independent validation results.

The left plot shows validation results from the 390 compounds dataset. The center and right plots show independent validation results from 1492 newly measured compounds. The center plot is for all independent validation compounds. The right plot shows all independent validation compounds reasonably similar to the model data. A nonlinear trend is apparent in all three plots where predictions for compounds RI < 400 tend to be overpredicted and predictions for compounds RI > 800 tend to be underpredicted. MAE: Mean absolute error; R²: Square of Pearson’s correlation coefficient; SE: Standard error.

ANN background

Since this paper describes ANN model optimization, a brief description of neural network methods is given here. ANN models enumerate a relationship between a set of targets y (dependent quantities) and a corresponding set of input variables x₁, x₂, x_n (independent quantities) [24]. There is an implicit assumption that y depends on x_n according to some function y = f(x_n) that the model will approximate.

ANN as a computational model

A neural network is a series of algebraic equations organized as a network of three or more layers of neurons (nodes). Every node of each layer is connected to every node of the next higher level layer and a weight is associated with each connection. Networks used for this study consist of an input layer with one node for each descriptor, a hidden layer to support nonlinearity and an output layer with a single node to output a solution. The solution for each case (data row) is generated by a forward pass that sequentially calculates an output value for each node in the network. The forward pass starts by loading the descriptors for one case to the input layer. Output is passed from input layer nodes through a sigmoid transfer function [25] that transforms each node input value to a value from to 0 to 1. The transformed value is passed to connected nodes in the hidden layer. A weight is associated with each connection and functions as a coefficient. Input to each hidden layer node is the sum of the products of the input layer outputs and connection weights and hidden layer output is also made through a sigmoid transformation. The input and final solution generated by the output node is created in the same way. A given set of descriptor input values results in a specific numerical value output from the output node. This is the solution for a case described by the input values and is determined by the weights on each connection.

ANN as a nonlinear learning system

ANN supervised learning adjusts the weights so as to approximate each target as a nonlinear function of the inputs. A significant advantage of ANN learning is the ability to enumerate this approximation without a priori knowledge of the exact form of the optimal nonlinear function [24]. In supervised learning, the network is presented with a sequence of case pairs consisting of a set of input values and a target value. The objective is to optimize the weight values so as to generate output for each case that is as close as possible to the target [24]. The output is compared with the target and an error is assessed to a cost function.

Models for this study used the back propagation gradient descent algorithm (BPGDA) [25]. The cost function and the weight space together enumerate an n-dimensional error surface where each point corresponds to a vector of weight values and an associated magnitude of the cost function. The network is ‘trained’ in a series of feed forward and back propagation passes that navigate ‘down’ the error surface. As described above, a feed forward pass is used to tabulate the error for each case. Back propagation utilizes gradient descent to determine the direction in which each weight must be adjusted in order to reduce the magnitude of the cost function. Gradient descent typically begins at a random point on the error surface and then modifies the weight values in the direction of steepest descent of the cost function [26]. The gradient, or direction in which the slope of the error surface is steepest in reduction of the cost function, is identified by calculating how changes in the weight values affect the error [25]. The gradient is the slope of the surface tangent to the current location in weight space and is therefore instantaneous. Since the location in weight space changes with each weight alteration, it is not possible to chart a path from the starting location to the cost minimum. Descent along the gradient must be approximated by making successive finite weight changes in the instantaneous direction of steepest descent. These weight adjustments are made in a series of steps with a magnitude proportional to the learning rate and gradually identify a location with a cost function minimum.

Weight adjustments can be determined and sequentially applied based on the error of each case (online updates) or adjustment values can be accumulated over all cases and applied simultaneously (batch updates) [26]. With either method, a training epoch is defined as applying weight adjustments once for all cases. Statistics are calculated at the end of each epoch.

Methods: nonoptimized neural net methods

Some aspects of ANN model development were not optimized in this study and for those aspects, the same methodology was used for all models constructed. These aspects are described in this section.

General ANN methodology

Neural net models for this study were trained according to the following general method. Each of the four fit/ validate sets described earlier was processed separately. Within each set, a total of 50 models were developed for each fold, each created from different random starting weights. Models were trained on the training set data and the test set MAE was evaluated at the end of each epoch. Test set data were used for ‘stopping,’ meaning that training continued until the test set MAE minimized. When minimization occurred, training stopped and predictions were made for the validation set. Of the 50 models generated for each fold, the model with the lowest test set MAE was selected as the final model. For each set, the process resulted in nine predictions for train compounds, ten predictions for validate compounds, and one prediction for each test compound. The nine train predictions were averaged, the ten validate predictions were averaged and statistics were calculated for the train, test and validate subsets. The process was repeated for each of the four fit/validate sets. To create final ensemble statistics, averages were taken over the 40 models of the ensemble (4 fit/validate sets × tenfolds). For each compound, 27 training set predictions were averaged for a final train prediction, and 3 test set predictions are averaged for the final test prediction. Validate set predictions are aggregated so that validate statistics can be calculated for the overall data split. The average of predicted values from all 40 models of the ensemble was used to make predictions for the independent validation data (newly measured data). The above methodology was used to create all models with the exception that optimizations were also evaluated using validate set statistics for stopping.

Weight update method

As discussed earlier, neural network learning by back propagation involves adjusting, or updating, the value of the weights of each network connection following an error gradient toward a global minimum. There are two major methods by which network weights can be updated. In deterministic gradient descent (batch updates), weights are updated based on the cumulative error of all rows of data. Weight changes identified by back propagation are accumulated over the entire training set and applied simultaneously [26]. In stochastic gradient descent (online updates) weights are updated are based on the error of each row individually. For many datasets, including this one, training with batch weight updates requires a substantially smaller learning rate than training with online updates [26]. When a small learning rate is used, a very large number of epochs can elapse before weight values converge to a minimum. On several tests with this data, a learning rate of 0.01 was required in order for any learning to occur with batch updates and training took up to four times longer to achieve similar results. Since many ANN modeling options were explored for this study and a large number of models were built, the use of batch weight updates and small learning rate values was prohibitive. All models were built using online weight updates at the start of learning. The possibility of switching to batch updates later in learning was also explored.

Methods: optimized ANN methods & incremental results

ANN optimization

Optimization is a process that may be described as the isolation of a preferable methodology from a set of available options. Optimization is an incremental empirical process where a single aspect of learning is targeted and multiple variations are attempted to determine which variation provides the best statistical outcome. A reasonable methodology is chosen for aspects of learning that are not being optimized and is kept constant as the optimized aspect is varied. Whatever optimum method is discovered is maintained when the next aspect of learning is optimized. Optimized methods eventually take the place of the ‘reasonable’ methods used at the start of the process. Since results of each optimization affect later steps, it is useful to have the results of each step presented in the context of the procedure description.

This study examines the empirical optimization of three aspects of ANN learning:

Annealing the learning rate

The method by which the magnitude of the learning rate is gradually reduced of as training continues.

Data split method

The method by which compounds are partitioned into the train/test/validate data split.

Network architecture

The complexity/nonlinearity of the neural network that is used to learn the problem.

A description of the procedure used to optimize each aspect is given in the following sections along with the results of the optimization.

Annealing the learning rate

The gradient descent algorithm (GDA) identifies the direction of steepest descent from the current error surface location using the first derivative of the error with respect to the weight values ∂E/∂w. This gives the direction for the next ‘step’ toward the error function minimum [26]. The size of the step is proportional to the learning rate. The magnitude of the learning rate plays an important role in finding the global minimum. A large learning rate speeds up training and may allow weight adjustments to ‘step over’ local minima. Later in training, a large learning rate can cause the network to step over the minima and never reach it. As the global minimum is approached, ∂E/∂w gets smaller and the size of each step increases relative to the steepness of the gradient. Under these conditions, large steps can be counterproductive. If training starts with a very small learning rate, the weight values will converge on the first minima encountered, even if this is a local minimum.

Annealing, or incrementally reducing the learning rate, is one solution to this issue. When annealing is used, training begins with a large learning rate that is reduced as the global minimum is approached. Because variation in the direction of steepest descent inherent with online updates can also complicate reaching the global minimum, annealing can also involve a switch to batch weight updates. Training methodologies such as Local Rate Adaptation [27, 28] automatically decrease the learning rate in proportion to the steepness of descent, but such methods involve constants whose value must be determined by trial and error. As an alternative for this study, a large learning rate was used until the test set MAE minimized. When the minimum was reached, the learning rate was reduced and training continued as long as the test MAE continued to diminish. If the test MAE minimized again, the learning rate was reduced and training progressed as long as improvements continued. Batch weight updates were also investigated by switching to batch updates at each minimum.

To optimize annealing by this method, the bitkey data split was trained with multiple annealing rate schedules. As a baseline, models were built using constant learning rates of 0.25, 0.1 and 0.01 (ON 0.25, ON 0.1, ON 0.01). An additional model was build using an initial learning rate of 0.25 that was reduced to 0.1 when the test set MAE minimized (ON 0.25, ON 0.1). An analogous schedule was tried where the update method was switched to batch along with the learning rate change (ON 0.25, BT 0.1). For a final set of schedules, a second drop in the learning rate was added if the test set MAE continued to drop after the first reduction. A model was built using online at 0.25, online at 0.1 and batch at 0.01 (ON 0.25, ON 0.1, BT 0.01) and another with online at 0.25, batch at 0.1 and online at 0.01 (ON 0.25, BT 0.1, ON 0.01). The top results are given in Table 1.

Table 1.

Results of training the bitkey data split with different annealing schedules.

Annealing schedule†	Stop‡	Train§			Test#			Validate¶			Average epochs††
		r2‡‡	MAE§§	SE##	r2	MAE	SE	r2	MAE	SE
ON 0.25	T	0.96	30	38	0.89	51	61	0.86	56	67	585
O N 0 .1	T	0.96	29	37	0.89	50	60	0.87	54	65	1018
ON 0.01	T	0.96	28	35	0.89	48	59	0.87	52	66	7375
ON 0.25, BT 0.1, ON 0.01	T	0.98	20	27	0.9	46	57	0.87	52	65	1685
ON 0.25	V	0.96	30	38	0.86	54	66	0.89	51	61	543
O N 0 .1	V	0.96	29	37	0.87	54	65	0.88	51	61	920
ON 0.01	V	0.96	28	36	0.86	54	67	0.89	49	60	7065
ON 0.25, BT 0.1, ON 0.01	V	0.97	26	33	0.87	53	66	0.90	46	59	1313

^†Schedule of changes in learning rate and weight update method as training progresses.

^‡Statistical set used to determine when to change learning rate and weight update method.

^§Training set statistics.

^#Test set statistics.

^¶Validation set statistics.

^††Average of epochs trained over all 40 models.

^‡‡Square of Pearson’s correlation coefficient.

^§§Mean absolute error.

^##Standard error (root mean square error).

The stopping criteria is the statistical metric used to determine when to when to stop training, switch the rate, or change the update method. For the annealing schedules described above, the test set MAE was used for stopping. The test set for each fold is small, consisting of only 7.5% of the overall dataset. For this reason, test set statistics can be erratic and not necessarily a representative indicator of model performance. Because of this, validation statistics were also evaluated as the stopping criteria. Training was performed using the same annealing schedule, but the validation set MAE was used to determine when to lower the learning rate and when to stop training. Results using validation stopping are also given in Table 1.

Annealing the learning rate resulted in a better validation SE compared with using a constant learning rate of 0.25 or 0.1. The best annealing schedule for both test and validate stopping was ON 0.25, BT 0.1, ON 0.01. The validation statistics for these models are shaded in gray. The statistics in bold text are highlighted because these models were built using a constant learning rate of 0.01. These models achieved similar validation statistics to annealing based models but required 4–5 times as many epochs to reach the stopping criteria. This could represent an unacceptable increase in computational time for a large dataset. It is intuitive that test set stopping resulted in better test statistics and validation stopping resulted in better validation statistics. It is unclear if the use of the validation statistics for stopping overestimates the predictive quality of the model. This will be addressed later in the study.

Variation in data split method

The bitkey data split was used for annealing schedule optimization. Optimization of the data split method was examined by building new models based on other data split methods. Each split was processed using the annealing schedule of ON 0.25, BT 0.1, ON 0.01 and models were built using both test and validate stopping. The following data split methods were evaluated.

Bitkey split

The best bitkey split models (ON 0.25, BT 0.1, ON 0.01 annealing) served as a baseline. This split is reasonably distributed in structure and activity space but only the presence/absence of heteratomic functional groups were used to characterize structure.

Activity split

Data were rank ordered on ascending RI value and split according to the method described in the Data split section. This creates the best possible distribution of RI values across the subsets of the split.

Random split

Rows were sorted in random order and split according to the method described in the Data split section. Since every random split is unique, two random splits were evaluated.

Ward’s split

Ward’s hierarchical clustering [29] was used to evaluate a data split method that takes into account all descriptor values. Hierarchical clustering starts with each compound in its own cluster. At each algorithmic step, the two most similar clusters are combined until all compounds are in one cluster. A dendogram is produced showing a schematic of how the compounds are related. To create a data split, clusters were aggregated starting from the first algorithmic step. Related small clusters were grouped when the average RI value between the clusters was similar. Compounds that had no immediate branch neighbors with similar values were left in their own cluster. The result was 112 aggregate clusters ranging from 1 to 9 members. The data split was established by a rank-order of each aggregate cluster on the RI value and sampling by the method used to create the bitkey split.

Models were built for each data split using the ON 0.25, BT 0.1, ON 0.01 annealing schedule described above. As with annealing optimization, models were built using both test set and validation set stopping. Results are given in Table 2 .

Table 2.

Results of training different data splits using the optimized annealing schedule.

Data split	Stop†	Train‡			Test§			Validate#			Independent3+¶			Independent 4+††
		r2‡‡	MAE§§	SE##	r2	MAE	SE	r2	MAE	SE	r2	MAE	SE	r2	MAE	SE
Activity	T	0.98	16	24	0.92	39	51	0.83	59	77	0.77	65	75	0.82	54	62
Random-1	T	0.97	24	32	0.91	42	53	0.87	53	67	0.78	66	73	0.83	56	61
Wards	T	0.98	21	28	0.92	40	52	0.87	52	67	0.77	63	73	0.83	53	61
Bitkey	T	0.98	20	27	0.90	46	57	0.87	52	65	0.78	63	72	0.84	52	59
Activity	V	0.98	19	27	0.87	50	67	0.87	51	67	0.77	65	74	0.82	54	62
Bitkey	V	0.97	26	33	0.87	53	66	0.9	46	59	0.78	65	74	0.84	53	59
Random-1	V	0.97	24	32	0.86	53	68	0.9	45	57	0.78	65	73	0.83	55	61
Wards	V	0.98	19	26	0.87	52	66	0.91	44	57	0.79	62	71	0.84	51	58

^†Stopping optimization criteria (test/validate).

^‡Training set statistics.

^§Test set statistics.

^#Validation set statistics.

^¶Independent validation statistics for compounds with three or more matching bitkeys in the training set.

^††Independent validation statistics for compounds with four or more matching bitkeys in the training set.

^‡‡Square of Pearson’s correlation coefficient.

^§§Mean absolute error.

^##Standard error (standard deviation of error).

As was the case with annealing optimization, better test set statistics occurred with test set stopping and better validation set statistics occurred with validate set stopping. Based on the results of data split optimization, the Wards data split trained using validation MAE optimization produces that best validation MAE and SE, but it is unclear if this use of the validation statistics creates a distorted picture of how the model will perform in practice. The difference between the best and worst models is not large and this contributes to the lack of clarity about best practices.

In order to help resolve this, independent validation (IVal) using new data was introduced. A set of 1492 compounds for which RI has recently been measured was used to assess the performance of these models under conditions similar to actual use. Experimental RI values for all IVal compounds fell within the RI range of model training data. When the ON 0.25, BT 0.1, ON 0.01 bitkey model with test set stopping was used to predict the IVal data, the r² was 0.69, the MAE was 78 and the SE was 83. These values are much poorer than any of the statistics above would suggest and this must be addressed.

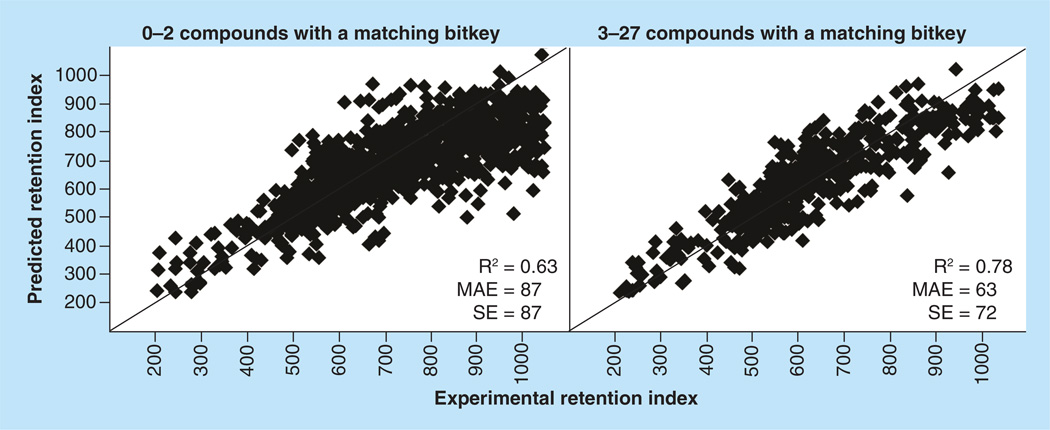
Applicability domain

Much of the discrepancy between model validation independent validation statistics can be explained by the model applicability domain (AD). The AD refers to the kind of chemical structures that would be expected to be well predicted based on the structures present in the training data. In order to evaluate the model AD, it is necessary to compare model dataset structures with structures being predicted. The bitkey values described earlier form the basis of a simple comparison method. A simple AD metric was tabulated for each IVal compound by counting the number of compounds in the model dataset with a matching bitkey. When bitkeys for two compounds match, both compounds possess the same combination of heteroatomic features. For a given IVal compound, if the model dataset contains no compounds with a matching bitkey, there are no compounds in the model with the same combination of features. This would be an indication that a good prediction is less likely. Figure 3 shows the predicted versus observed plots and statistics for two sets of IVal compounds. The set on the left shows predictions for IVal compounds with 0–2 compounds in the model data with a matching bitkey. The set on the right shows predictions for IVal compounds with 3–27 dataset compounds with a matching bitkey. The difference in MAE and SE between the two groups is significant. This figure illustrates the necessity of evaluating the AD of compounds predicted by a model. The issue is complex because even for the 413 IVal compounds with no model data compounds with a matching bitkey (no compounds with the same combination of heteroatomic features), 160 of them are predicted within the validate MAE of the model (residual of 52 RIU or less) and 362 are predicted within ± 3 SE.

Figure 3. Independent validation on 1492 newly measured compounds.

The plot on the left shows IVal compounds where there were 0–2 compounds in the model dataset with a matching bitkey. The plot on the right shows compounds with 3–27 model compounds with a matching bitkey. When there are at least three matching compounds present in model data, at least one of matching compound will always be present in the training set. MAE: Mean absolute error; R²: Square of Pearson’s correlation coefficient; SE: Standard error.

Optimizing the network architecture

Architecture is the number of layers and the number of neurons in each layer. Models developed up to this point used an architecture of a 36 input nodes, 35 hidden layer nodes and 1 output node (36.35.1). For architecture optimization, network configurations with a smaller number of hidden neurons were tested. The number of hidden neurons was cut approximately in half three times resulting in architectures of 36.18.1, 36.9.1 and 36.4.1. Since the model based on the Wards data split had the lowest MAE for both dataset validation and independent validation, architecture optimization was based on the Wards split trained using the annealing schedule determined earlier. As with annealing, and data split optimization, separate models were created using test set and validation set stopping. The best and worst results are given in Table 3.

Table 3.

Results of training data splits with different network architectures.

Arch†	Split‡	Stop§	Train#			Test¶			Validate††			Independent 3+‡‡			Independent 4+§§
			r2##	MAE¶¶	SE†††	r2	MAE	SE	r2	MAE	SE	r2	MAE	SE	r2	MAE	SE
MLR	MLR‡‡‡	-	0.98	27	35	-	-	-	0.83	61	73	0.73	72	83	0.79	62	72
3 6 . 35 .1	random-2‡‡‡	V	0.98	27	35	0.86	54	68	0.89	48	62	0.77	67	73	0.82	58	63
3 6 . 35 .1	random-2	T	0.98	21	28	0.92	39	50	0.86	54	70	0.78	64	73	0.83	56	62
3 6 .9.1	Wards	T	0.97	23	30	0.92	40	52	0.88	49	64	0.79	61	69	0.85	51	58
3 6 . 4 .1	Wards	T	0.97	27	34	0.92	40	51	0.88	49	62	0.8	60	67	0.85	50	57
3 6 . 35 .1	random-2	V	0.97	24	32	0.86	54	68	0.9	46	59	0.78	65	74	0.83	55	61
3 6 . 4 .1	Wards	V	0.97	25	33	0.87	51	66	0.91	43	55	0.82	57	66	0.87	47	56
3 6 .9.1	Wards	V	0.98	21	28	0.87	51	67	0.91	42	54	0.8	59	69	0.86	48	55

^†Network architecture.

^‡Data split.

^§Stopping criteria.

^#Training set statistics.

^¶Test set statistics.

^††Validation set statistics.

^‡‡Independent validation statistics for compounds with three or more matching bitkeys in the training set.

^§§Independent validation statistics for compounds with four or more matching bitkeys in the training set.

^##Square of Pearson’s correlation coefficient.

^¶¶Mean absolute error.

^†††Standard error (root mean square error).

^‡‡‡Given for comparison are results from the MLR model and the random-2 split model trained with online weight updates and constant 0.25 learning rate.

Independent validation results for IVal compounds with three or more and four or more matching bitkeys are also included. A decrease in network nonlinearity resulted in improved validation MAE and SE for both test and validate stopping. Since the 36.9.1 and 36.4.1 architectures resulted in the largest improvement for the Wards data split, 36.9.1 and 36.4.1 models were also built for the bitkey and random splits. These did not show better validation performance and the Wards data split. Similar to data split and annealing optimization, validation stopping resulted in better dataset and independent validation statistics than the use of test set stopping.

Aggregate results of optimization

After all optimizations were concluded, the best ANN model with regard to validation SE utilized a 36.9.1 network architecture, the Wards data split, and was trained with the ON 0.25, BT 0.1, ON 0.01 annealing schedule with validate set stopping (36.9.1/Wards/V-stopping). There was meaningful improvement compared with the MLR model with a validation SE difference of 19 RIU (73 with MLR, 54 with ANN). The best ANN model with regard to I-Val SE utilized a 36.4.1 network architecture but was the same in all other respects (36.4.1/Wards/V-stopping). For I-Val, there was improvement from the MLR SE of 83/72 down to 66/56 for ANN (3+ matching bitkey/4+ matching bitkey).

The optimized ANN models also performed better in independent validation than the baseline ANN models built with random data splits and trained with a constant learning rate. The 35.36.1/ random-2/V-stopping ANN model listed at the top of Table 3 had the best validation statistics for the random split models trained without learning rate annealing. Independent validation of this model resulted in an IVal SE of 73/63. In contrast, the best optimized model with respect to independent validation was the 36.4.1/Wards/V-stopping model with an IVal SE of 66/56.

Discussion

Results suggest that ANN is a more effective approach then MLR for modeling this RI data. The permutations examined in this study reveal no consensus as to the specific method for obtaining the best ANN model. The differences among the best models are likely not significant, suggesting that a good model of these data can be built by multiple ANN methods. The 36.9.1/ Wards/V-stopping model had the best statistical results for the model validation set, but performed second best in independent validation where the 36.4.1/Wards/V-stopping model was slightly better. The differences between the top ANN models are small enough that the difference in probable predictive quality during actual use cannot be determined. If a different set of compounds was used for independent validation, the ‘best’ model could have been different as well.

For this dataset, independent validation suggests that the use of validation statistics for stopping produces models that work better in practice than models built with test set stopping. Though the differences were not large, for every model pair tested, independent validation statistics were better for models built with validate stopping than with test stopping. It can be argued that there is less difference between the model validation statistics and independent validation statistics for models using test set stopping implying that the validation statistics for models created with test set stopping give a more accurate assessment of model performance. While this is true, models created using validate set stopping performed slightly better in independent validation. It is clear that some of these conflicting issues must be resolved by individual researchers who will determine which scenario most closely suits the needs of their current project.

Despite the lack of clarity among the best ANN models, there is a meaningful difference between the optimized and nonoptimized models. The 35.36.1/ random-2/V-stopping model listed at the top of Table 3 had the best validation statistics for the random split models trained with a constant learning rate. Independent validation of this model resulted in an IVal SE of 73/63. The 36.4.1/Wards/V-stopping model achieved an IVal SE of 66/56. This demonstrates that optimizing the data split method, annealing schedule and network architecture resulted in a seven-point improvement for IVal SE compared with a randomly assigned data split trained with a constant learning rate. This improvement represents a 10.4% reduction in SE. In the context of MolFind/BioSM, a 7 RIU reduction in SE corresponds to a ±3 SE filter window that is 42 RIU narrower. Based on these results, the 36.4.1/Wards/V-stopping model would function as the most effective filter in MolFind/BioSM.

The differences between the deterministic and random splitting methods were not large enough to be conclusive, but it is clear that the use of a deterministic splitting method was not counterproductive. After all optimizations, the random-2 split had the worst IVal performance, but performance was still reasonable the difference does not reveal any dramatic liability arising from the use of a random split. The activity based split appears to be the least favorable.

An interesting phenomenon is observed when comparing the difference in prediction results across the A, B, C and D sets of each data split for the random, Wards and bitkey split models created using the best architectures (36.4.1, 36.49.1). For the data splits created with the Wards and bitkey methods, the largest difference in SE across the four sets of any one ensemble was 9 RIU. This is an indication that the SE was relatively similar for all four sets. For models based on the two random splits, the largest SE difference was 23 RIU. For this dataset, there was a greater variation in SE across the four sets of the random splits as compared with the deterministic splits. This underscores the potential utility of the 4 × 10 × 10 ensemble method when random data splits are used.

Comparing the results of this study to current literature has proven difficult. Other than previous publications by our group [3, 7], it has been difficult to find published ANN RI models of large diverse datasets to form the basis of a comparison. In a search of published RI models, the largest ANN model not from our group was based on 70 pesticides [13]. This study also utilized gas chromatographic retention index data and not HPLC. While this study references optimization of the number of hidden neurons, learning rate and momentum, no information was given as to the details of the optimization procedure. It is difficult to compare the models from this current study to previous publications of our group because previous models were built using nitro-n-alkane standard RI measurement. The numerical RI scale produced from the current n-alkylamide references is substantially different from the previous scale making direct comparisons unhelpful. The lack of published methodologies and examples to draw upon remains an issue with solving the problems of ongoing model development.

Since the MolFind/BioSM method requires the smallest possible prediction SE, minor optimizations are useful. The smaller the validation SE, the more compounds will be filtered out by the model. As the structure identification problem remains a significant obstacle in the field of metabolomics, the development of an application that can substantially narrow down a candidates list for an experimentally observed unknown would be a major development. The optimizations described in this report will be applied to a new model that includes the 1492 newly measured compounds that were used for independent validation in this study. It is hoped that the increase in the model structure space will result in further improvements in the validation standard error and a significant increase in the model applicability domain.

Conclusion

In this study, we have reported on the results of optimizing three aspects of ANN modeling methodology to improve the computational model implemented in the MolFind/BioSM application. This application is part of an effort to determine the structure of experimentally observed unknowns in nontargeted metabolomics. Optimized aspects of ANN model development were:

• Learning rate annealing schedule;

• Data split method;

• Network architecture;

Model optimizations were evaluated with independent validation on new data. Results were compared with a baseline MLR model and to the results of nonoptimized ANN modes. This report also described additional aspects of model building including structure descriptors, input normalization and scaling, and the nonoptimized aspects of model generation that were implemented. A significant goal of this report was to provide sufficient detail to allow the reader to repeat the described model building and optimization methods or to apply them to studies on comparable data.

Future perspective

Progress in nontargeted metabolomics is currently limited by the inability to identify the structures of most detected compounds. MolFind/BioSM was created to address this problem. The use of differentially expressed experimental features (such as exact mass and/or retention time) among treatment groups has led to the development of multiple putative disease biomarkers [30,31]. However, until the chemical structure corresponding to each feature of interest can be reliably determined, it will remain difficult to identify relevant metabolic pathways or understand disease mechanisms and biological significance. The continued development and optimization of predictive models in Mol-Find/BioSM will lead to better model performance and greatly increase our ability to identify the structures of currently unknown compounds in biological fluids. These advances should ultimately enhance the scientific impact of metabolomics research.

Executive summary.

• The MolFind/BioSM application utilizes an innovative approach for structural identification of chemical unknowns. MolFind/BioSM uses the experimental exact mass of an unknown to create a candidate list of possible matches and removes false positives by filtering the list with computational models. Because the predictive standard error of the models determines filtering effectiveness, optimization of the MolFind/BioSM HPLC retention index (HPLC-RI) model is investigated.

• HPLC RI measurements were made for 390 diverse compounds to form the basis of the HPLC-RI models. Measurements utilized a homologous series of n-alkylamide reference compounds to convert retention times to RI. Additionally, newly measured HPLC-RI data for 1492 compounds was made available for independent validation of all models.

• A set of 36 SIR descriptors was used for model generation. Descriptors were selected to characterize every feature of every molecule that would likely influence retention time under known measurement conditions. Descriptors included the E-State IGroups, molecular connectivity indices and graph-based descriptors.

• Multiple artificial neural network models of HPLC-RI data were built and evaluated in the model optimization process. Optimized model results were compared with nonoptimized ANN model results and to results from an MLR model. Neural network learning methodologies that were optimized included the learning rate annealing schedule, data split method and network architecture.

• The best model with regard to independent validation of 1492 newly measured compounds utilized a network architecture of 36.4.1, was based on a Ward’s clustering data split, and was trained with a learning rate annealing schedule of Online 0.25lr, Batch 0.1lr, Online 0.01lr with validate set stopping. This model demonstrated a 10.4% improvement in standard error compared with the best nonoptimized ANN model and a 25.8% improvement over the MLR model.

Key terms

CID (MS/MS) spectra

Collision Induced Disassociation Spectra, mass spectroscopy fingerprint technique based on the detection a profile of molecular fragments produced the gas phase. This technique is an important means of structure characterization in bioanalytical systems.

Multiple Linear Regression

Multiple Linear Regression (MLR), a model generation technique capable of capturing the optimal linear relationship between a single dependent variable and multiple independent variables. MLR assumes some degree of linear relationship between the dependent and independent variables.

Structure information representation descriptors

Structure Information Representation (SIR) is a method of molecular representation which encodes structure information necessary for modeling noncovalent interactions. SIR descriptors are calculated from the molecular connection table without specification of a 3D geometry and encode information about electron accessibility and skeletal variation.