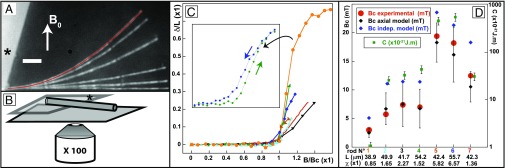
Fig. 3.

Experiments with microrods. (A) Montage of six superposed micrographs (back-scattered light) of a microrod [L = (42.3 $\pm$ 0.05)$\mu$m, r = (0.3 $\pm$ 0.01)$\mu$m, C = (30.3 $\pm$ 5.7)10⁻²¹ Jm, ${\chi }_0$ = 1.35 $\pm$ 0.2] deformed by a magnetic field $B_0$ applied at ${\theta }_0$ = 0 and varying from 10 to 20 mT with a regular increment of 2 mT. On the 20-mT rod, the theoretical shape from the axial model is superposed in red (mean difference 0.16$\mu$m, max 0.5$\mu$m, whereas the max divergence of the undeformed rod from a straight line is 0.13$\mu$m. The pictures for 0–10 mT are indistinguishable. White bar = 5$\mu$m. The mark (*) indicates the coverslip onto which the rod sticks as sketched on B. (C) Deflection of the tip of seven rods while the orthogonal magnetic field is increased. (Inset) An entire cycle of field increase and decrease is shown for rod one, and shows a weak hysteresis (due to plastic deformation). (D) Comparison between the theoretical critical field from the axial model (black lozenges), the independent model (blue lozenges), and the measured buckling field (red dots) referring to the left y axis. The error bars on the theoretical values originate from the uncertainty on the measured properties of the rod (L, r, C, and $\mathit{\chi }$) and the errors on the measured field are on the order of the size of the dots. All observed buckling fields are compatible with the axial model (average difference: 3%, range −20–20%). Rod length (L) and the susceptibility $\left({\chi }_0\right)$ are written under the rod number (same color as on graph C), whereas their bending modulus (C) is plotted (green squares) with the log scale on the right axis.