Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Jul 1.
Published in final edited form as: Genet Epidemiol. 2015 May 13;39(5):325–333. doi: 10.1002/gepi.21903

Robust and powerful affected sibpairtest for rare variant association

Keng-Han Lin 1,3, Sebastian Zöllner 1,2,3
PMCID: PMC4469535  NIHMSID: NIHMS681495  PMID: 25966809

Abstract

Advances in DNA sequencing technology facilitate investigating the impact of rare variants on complex diseases. However, using a conventional case-control design, large samples are needed to capture enough rare variants to achieve sufficient power for testing the association between suspected loci and complex diseases. In such large samples, population stratification may easily cause spurious signals. One approach to overcome stratification is to use a family-based design. For rare variants, this strategy is especially appropriate, as power can be increased considerably by analyzing cases with affected relatives. We propose a novel framework for association testing in affected sibpairs by comparing the allele count of rare variants on chromosome regions shared identical by descent to the allele count of rare variants on non-shared chromosome regions, referred to as test for rare-variant association with family-based internal control (TRAFIC). This design is generally robust to population stratification as cases and controls are matched within each sibpair. We evaluate the power analytically using general model for effect size of rare variants. For the same number of genotyped people, TRAFIC shows superior power over the conventional case-control study for variants with summed risk allele frequency f < 0.05; this power advantage is even more substantial when considering allelic heterogeneity. For complex models of gene-gene interaction, this power advantage depends on the direction of interaction and overall heritability. In sum, we introduce a new method for analyzing rare variants in affected sibpairs that is robust to population stratification, and provide freely available software.

Keywords: rare variants, dichotomoustraits, family studies, association test, sequencing

Introduction

Rare variants with large relative risk are hypothesized to explain some of the missing heritability of complex diseases [Mardis et al., 2009]. Several studies have identified rare variants underlying rare Mendelian diseases using next-generation sequencing technology [Wong et al., 2009, Tabor et al., 2010]. However, the conventional case-control design has low statistical power to detect the association between rare variants and complex diseases [Li and Leal, 2008, Cooper and Shendure, 2011]. To overcome the low power of single-marker test on rare variants, researchers have proposed to combine variants in a gene or genomic region to test for association [Li and Leal, 2008, Zawistowski et al., 2010, Price et al., 2010]. However, such gene-based tests in population samples may still need >10,000 individuals to identify the signal from rare variants [Nelson et al., 2012]; sequencing such large samples is still very expensive. Moreover, large samples are typically more heterogeneous in origin, increasing the risk of population stratification [Price et al., 2006]. In such large samples, even subtle stratification causes substantially increased false positive rate in rare variant tests [Zawistowski et al., 2010]. While methods to control for population stratification, such as principal components and genomic control [Devlin and Roeder, 1999, Price et al., 2006] have been successfully applied for common variants, it is unclear whether such methods are appropriate for rare variant tests [Mathieson and McVean, 2012, Liu, Nicolae and Chen, 2013].

As family members are naturally matched for genetic background, several recent gene-based methods for testing the association between rare variants and the phenotype adapt family data to control for population stratification [Guo and Shugart, 2012, De et al., 2013]. In addition, the allele frequency of rare risk variants in cases can be substantially increased by collecting cases with affected relatives [Fingerlin, Boehnke and Abecasis, 2004, Peng et al., 2010, Zöllner, 2012]. While collecting families with multiple affected members is challenging, family-based studies of rare variants can leverage existing large collections of families that were originally generated for linkage analysis [Rao et al., 2003, Howson et al., 2009, Guan et al., 2012]; for example, International Type 2 Diabetes Linkage Analysis Consortium contains >4000 affected sibpairs [Guan et al., 2012].

Methods have been proposed to extend the current collapsing tests to rare variants in family data. Guo and Shugart [2012] and De et al [2013], extended the family-based association test (FBAT) [Laird and Lange, 2006] to rare variants in the style of a collapsing test. Schifano et al. [2012] and Chen et al. [2013] used linear mixed models to extend the SNP-set kernel association test (SKAT) [Wu et al., 2011] to families. Shugart et al. [2012] and Fang et al. [Fang, Sha and Zhang, 2012] proposed to estimate the relatedness between samples and adjust the test statistics for rare variant association accordingly. However, none of the existing methods directly leverage the benefit of studying families where the same rare variant is observed multiple times. By using such information, we can increase power to detect the association between rare variants and the phenotype.

Here, we propose a powerful framework for testing rare variant associations using affected sibpairs. We create a matched design by comparing the allele count of rare variants on shared identity by descent chromosome regions to the allele count on non-shared identity by descent chromosome regions across affected sibpairs in a region of interest. Sharing status of chromosome regions can be easily estimated using high density genotype data [Keith et al., 2008], and sharing status of alleles can be inferred conditional on the known chromosome region sharing status. Intuitively, we consider shared chromosome regions as “case” chromosome regions and non-shared chromosome regions as “control” chromosome regions. Under the null hypothesis of no association, the probability of a shared chromosome region carrying an allele is identical to the probability of a non-shared chromosome region carrying an allele. Under the alternative that an allele increases/decreases the disease risk, the probability of a shared chromosome region carrying that allele is higher/lower than the probability of a non-shared chromosome region carrying that allele.

We evaluate this design by calculating the analytical power for a collapsing gene-based test [Li and Leal, 2008], assuming a general model of rare risk alleles that is specified by the summed allele frequency of all rare risk variants in the gene and the mean and variance of their effect size [Zöllner, 2012]. We show that given the same number of sequenced individuals, the power of the proposed affected sibpair test for rare-variant association with family-based internal control (TRAFIC) is higher than the conventional case-control design for rare risk variants (summed risk allele frequency < 0.05). Considering allelic heterogeneity, where risk variants have different effect sizes, TRAFIC doubles the power of a case-control study in many realistic parameter values. We also evaluate the power of the proposed method under various gene-gene interaction models and find that power depends on the type of interaction and the overall heritability of the disease. Using simulations, we also show that the proposed TRAFIC is generally robust to population stratification.

Materials and Methods

Test for rare-variant association with family-based internal control (TRAFIC)

We consider a set of affected sibpairs with known number of chromosome regions shared identical by descent (IBD). At a locus of interest (for example a gene), we compare the count of alleles of rare variants on chromosome regions shared IBD between the siblings to the count of alleles of rare variants on chromosome regions not shared IBD (non-IBD chromosome regions) across sibpairs. Let, pIBD be the frequency of IBD chromosome region carrying at least one allele and pNonIBD be the frequency of non-IBD chromosome regions carrying at least one allele. Alleles without effect on disease risk are equally likely to occur on any chromosome region regardless of IBD status. Thus, the null hypothesis under no association is H0 : pIBD = pNonIBD. Variants that are associated with the phenotype (protective or causative) would differ in frequency between IBD and non-IBD chromosome regions. Hence, we can test for departure from the null hypothesis either in a collapsing framework by considering the alternative Ha : pIBD ≠ pNonIBD or in a dispersion framework where this alternative is considered for each variant and the combined test statistic aggregates the evidence across all variants.

In a sibpair with known IBD status, identifying whether an allele of a variant is located on an IBD or a non-IBD chromosome region is straightforward for most genotypes as shown in Table 1; for example, when a sibpair does not share the chromosome region (0 IBD chromosome region), all observed alleles for that variant in two siblings are non-shared; for a sibpair who shares 1 IBD chromosome region, the alleles of a homozygous sibling must be one shared and one non-shared. Only when the sibpair shares one IBD chromosome region and the genotypes are heterozygous in both individuals, the IBD status of the allele is ambiguous (shaded in Table 1): this configuration could be either the result of a single rare allele located on the IBD chromosome region or two copies of the rare allele inherited separately on the non-IBD chromosome regions (as illustrated in Appendix Figure 1). To resolve this ambiguous configuration, we implement an imputation algorithm and use simulations to show the false positive rate is controlled (see Appendix 1 for details).

Table 1.

Identification of variant IBD status conditional on chromosome

0 IBD
chromosome
region		 1 IBD chromosome
region		 2 IBD chromosome
regions
Both siblings are homozygous minor allele 4 non-shared alleles 1 shared and 2 non-shared alleles 2 shared alleles
One homozygous minor allele and one heterozygote 3 non-shared alleles 1 shared and 1 non-shared alleles N/A
Both siblings are heterozygous 2 non-shared alleles Ambiguous configuration 1 shared allele
Open in a new tab

Assuming chromosome region IBD status is known, the number of shared and non-shared alleles can be inferred for all but one configuration of genotypes (shaded cell).

Evaluating TRAFIC

The analytical power of the proposed TRAFIC based on a collapsing gene-based test depends on the difference between the expected allele count on shared IBD chromosome regions and the expected allele count on non-shared IBD chromosome regions. To calculate these expectations, we assume that all rare variants evaluated in a locus occur on different haplotypes. Let f be the sum of population allele frequencies of all risk variants (summed risk allele frequency). For each sibpair, we count the number of alleles HS ∈ {0,1,2} on the shared chromosome regions and the number of alleles HNS ∈ {0,1,2,3,4} on non-shared chromosome regions. Let AAR be an affected sibpair and P(HS,HNS|AAR,S) be the probability of HS,HNS conditional on the number of shared IBD chromosome regions S ∈ {0,1,2}.

Using Bayes’ rule, we can write this conditional probability as

P(HS,HNS|AAR,S)=P(AAR|HS,HNS)P(HS,HNS|S)P(S)1P(AAR,S),

where P(AAR|HS,HNS) depends on the underlying genetic and effect size model (see Appendix 2 for derivations). Based on previous work [Zöllner, 2012], we model the effect size (relative risk) of each risk haplotype as a random variable with the first two moments μ and σ2. Then, P(HS,HNS|AAR,S) is fully determined by the parameters μ, σ2, and f (See Appendix 2). We calculate the power for TRAFIC based on P(HS,HNS|AAR,S) for a range of relative risk parameter μ and σ2, and under different f assuming a simple collapsing method [Li and Leal, 2008] to test the association between rare variants and the dichotomous phenotype (Appendix 3). To maintain an overall false positive rate of 0.05 after testing 20,000 genes in the genome, we set the false positive rate to 2.5×10−6. We compare our proposed TRAFIC with two other designs: (1) the conventional case-control study comparing a sample of cases to unaffected controls. (2) A selected cases design comparing cases that are ascertained to have an affected sibling to unaffected controls [Fingerlin, Boehnke and Abecasis, 2004, Zöllner, 2012]. All designs retain the nominal false positive rate under the null (Appendix Table 1).

Simulation setup for TRAFIC

To validate the derived analytical results, we simulate sibpair samples and apply our proposed TRAFIC. We first generate four independent parental haplotypes, each carrying a risk allele with probability f. Without considering recombination, we then generate two descendants, each randomly inheriting one chromosome region from each parent. Following Risch [1990], we define the contribution to prevalence K at the locus of interest as KL and the contribution of the remaining genome as KG. The prevalence among subjects with an affected relative with relation status R is KR; the contribution to KR at the locus of interest and the remaining genome are then KLR and KGR respectively. We adjust KGKGR under the multiplicative model to maintain both K and the sibling relative risk (SRR).

SRR=KLKLRKGKGRK×K.

Here KLKLR depends on P(AAR|HS,HNS) (more details in Appendix 2). The relative risk of the risk allele follows a gamma distribution with specified μ and σ2. Thus, the probability of having both siblings in the family affected is KLKLRKGKGR and is set to 1 if the simulated probability exceeds 1. We generate datasets of 1000 affected sibpairs in each replicate. To evaluate the performance of our multiple imputation algorithm, we generate sibpairs assuming the sharing status is known. Then we mask the true location for the double-heterozygote sibpairs who share one IBD chromosome region and apply our multiple imputation algorithm.

Population stratification

Using the simulation design described above, we evaluate the impact of population stratification. We simulate two populations with summed risk allele frequency of 0.01 and 0.05, respectively, and assign a ratio of prevalence π between two populations. Assuming two populations have the same sibling relative risk, the ratio of frequencies of affected sibpairs between the two populations is then π2. Assuming that both populations contribute equally, we generate case-control samples by sampling 1000 cases, a proportion of π / (1 + π) from population 1 and 1 / (1 + π) from population 2. We also sample 1000 controls with equal contribution from each population. To generate a stratified sample for TRAFIC, we generate a sample of 1000 affected sibpairs with a proportion of π2 / (1 + π2) from population 1 and a proportion of 1/(1 + π2) from population 2. We assume unknown sharing status for double-heterozygote sibpairs who share one IBD chromosome region and impute the sharing status through multiple imputation. To generate cases for the selected cases design, we sample affected sibpairs with a proportion of π2 / (1 + π2) from population 1 and 1 / (1 + π2) from population 2; controls are sampled evenly from both populations. We generate 1000 datasets for each value of π and estimate the false positive rate.

Gene-gene interaction

Interaction between the locus of interest and the remaining genome can influence the power of association tests in family samples [Risch N, 2001, Zöllner, 2012]. We model gene-genome interaction as two loci, L and G. L is the locus of interest while G represents genetic effects in the remainder of the genome. We define the joint effect as

P(A|hm,hn,gs,gt)∝βLhm+hnβGgs+gtγ(hm+hn)(gs+gt).

where hm and hn represent the indicator of a risk allele at locus L; let gs and gt represent the indicator of a risk allele at locus G. In the absence of risk alleles at G, all risk alleles at locus L have the same relative risk βL. Moreover, we describe the extent of interaction in this model by the parameter γ as the relative risk when risk alleles are present at both loci L and G, where γ = 1 indicates no interaction, γ < 1 indicates antagonistic interaction, and γ > 1 indicates synergistic interaction.

Under this model, the marginal relative risk at locus L is

P(A|hm=1)P(A|hm=0)=βL∑hnβLhnp(hn)∑gs∑gt(βGγ)gs+gtγhn(gs+gt)p(gs)p(gt)∑hnβLhnp(hn)∑gs∑gtβGgs+gtγhn(gs+gt)p(gs)p(gt).

The marginal relative risk at locus G is expressed in a similar fashion. To explore the effect of gene-gene interaction, given the sibling relative risk, we vary γ while adjusting βL and βG to keep the marginal relative risks constant (see Appendix 4). This maintains a constant power for the conventional case-control study. We then calculate P(HS,HNS|AAR) at locus L and evaluate the power of TRAFIC for different values of γ.

An example to illustrate TRAFIC

To illustrate how to apply TRAFIC, we simulate 1000 sibpairs assuming the number of shared IBD chromosome region is known. We simulate sequence data by using coalescent-model based simulator COSI [Schaffner et al., 2005] to generate a population of ten thousand 1kb haplotypes. From the 50 variants in the region, we randomly pick 10 variants with minor allele frequency (MAF) < 0.05 and assign each variant the relative risk as a function of MAF, −log10(MAF) [Wu et al., 2011]. In this setting, a variant with MAF = 0.05 has relative risk of 1.33 and a singleton has relative risk of 4. Hence, in this dataset, f = 0.025, μ = 2.52, and σ2 = 0.62. We then generate 1000 affected sibpairs and apply TRAFIC to that dataset.

The simulated data contains 254, 509 and 237 sibpairs who share 0, 1, and 2 chromosome regions, respectively; these equal to 983 shared chromosome regions and 2034 non-shared chromosome regions. Excluding 42 sibpairs who shared one chromosome region with ambiguous double-heterozygote genotypes, there are 51 shared and 67 non-shared chromosome regions carrying at least one allele (carrier). Using imputation to resolve the IBD status of allele from 42 sibpairs with ambiguous double-heterozygote genotypes, the mean count of carrier chromosome regions is 91.7 on shared chromosome regions and 67.6 on non-shared chromosome regions. Using a χ2 test, we reject the null hypothesis that IBD and non-IBD chromosome regions are equally likely to carry at least one allele (p = 5.63 × 10−11) indicating the presence of risk variants at this locus.

Results

We proposed a new gene-based method for analyzing affected sibpairs by comparing the risk alleles on shared IBD chromosome regions with the risk alleles on non-shared IBD chromosome regions. We evaluated the proposed TRAFIC design assuming a collapsing gene-based test by modeling allelic heterogeneity at the locus of interest based on a summed allele frequency of all risk variants f and a distribution of effect sizes with mean μ and variance σ2. For comparison, we also evaluated the conventional cases-control design (conventional) and a case-control design in which the cases are selected conditional on having an affected sibling (selected cases) under the same genetic model. For all three designs, we assumed equal number of sequenced or genotyped individuals. To use consistent language, we referred to shared IBD chromosome regions in TRAFIC as cases and to non-shared IBD chromosome regions as controls.

First, we compared the expected summed minor allele frequency (sMAF) in cases and controls with and without allelic heterogeneity to illustrate how TRAFIC behaved relative to the conventional and selected cases designs. We then calculated the analytical power of three designs for comparisons. We also checked robustness to population stratification. Finally, we calculated the analytical power of TRAFIC while considering different directions of gene-gene interaction.

Frequency distribution of risk variants

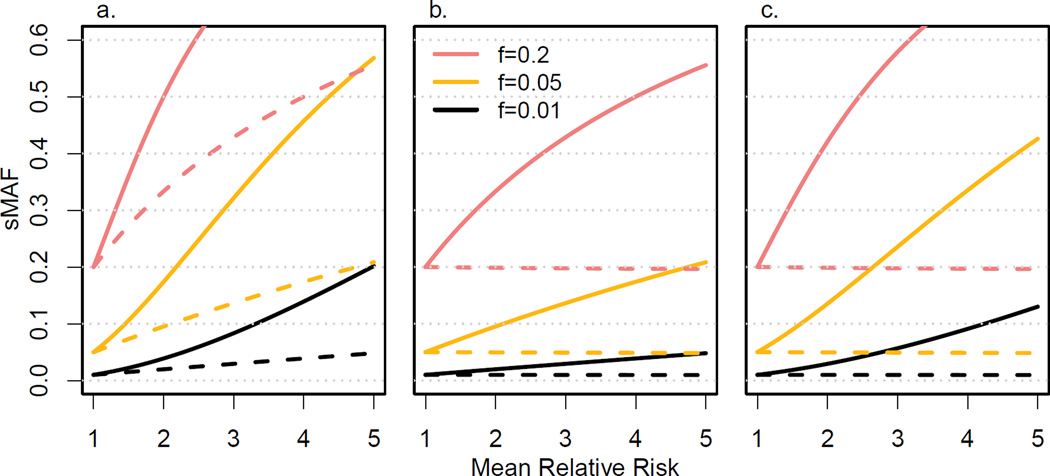
To quantify the enrichment of risk variants in TRAFIC, we calculated the expected summed minor allele frequency (sMAF) of risk variants in cases and controls of TRAFIC for a range of genetic models (see Appendix 3 for details). Initially, we modeled a locus with constant genetic risk μ between 1 and 5 for all variants (σ2 = 0) (Figure 1) and a disease prevalence of 0.01. In TRAFIC (Figure 1a), sMAF increased rapidly in cases (shared IBD chromosome regions) and also increased roughly linearly with μ in controls (non-shared IBD chromosome regions). In the conventional design (Figure 1b), sMAF increased in cases almost linearly with relative risk, only slightly faster than the sMAF in controls of TRAFIC. In the selected cases design (Figure 1c), sMAF in cases with affected siblings increased faster than cases in the conventional case-control design but slower than sMAF in cases of TRAFIC. Both in the conventional design and the selected cases design, sMAF in controls decreased slightly as μ increased, especially for more common variants f = 0.20. As a result, TRAFIC generated a larger difference in sMAF between cases and controls than the conventional case-control design in models with f = 0.01 and 0.05. This advantage of TRAFIC reduced with increasing f. For μ = 2, the difference in sMAF of TRAFIC compared to the conventional design was 190% (0.019 to 0.010) at f = 0.01 and reduced to 123% (0.166 to 0.135) at f = 0.20. For a higher disease prevalence of 0.20, the sMAF in controls decreased more rapidly as μ increased and the difference between cases and controls grew further in the conventional case-control and selected cases design (Appendix Figure 2).

Figure 1.

Figure 1

Open in a new tab

Summed minor allele frequency (sMAF) of risk variants in cases (solid lines) and controls (broken lines) under different study designs. We show sMAF as a function of mean relative risk of risk variants for (a) TRAFIC, (b) the conventional case-control design, and (c) the selected cases design for summed allele frequencies (f) of 0.01, 0.05 and 0.2 and fixed variance of relative risk σ2 = 0.

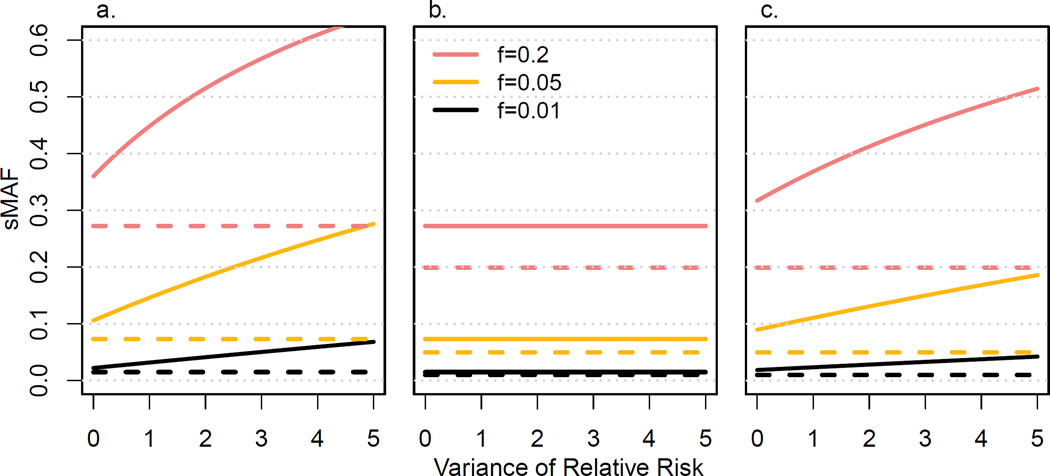
To evaluate scenarios where genetic effect differs between risk variants, we considered a distribution of relative risks with σ2 > 0 while maintaining μ = 1.5 (Figure 2); for f = 0.01, a value σ2 = 0.1 represents e.g. a scenario of 20 tested variants with equal frequencies where 6 of the tested variants are non-functional (relative risk = 1) and 14 of the tested variants have a relative risk of 1.71. A value σ2 = 0.2 would e.g. represent 9 non-functional variants and 11 variants with relative risk 1.91. For σ2 = 0, the difference in sMAF between cases and controls increases with f in all three designs. Increasing σ2 did not affect sMAF in cases or controls in the conventional design, as in this design sMAFs only depended on μ (Figure 2b). In TRAFIC, sMAF in cases increased with σ2 while the sMAF in controls remained constant. Similarly, in the selected cases design, sMAF in cases increased withσ2, albeit more slowly than for TRAFIC (Figure 2a and 2c). Even if the average effect of risk variants is 1 (μ = 1), the difference in sMAF between cases and control increases with growing σ2 for TRAFIC and for the selected cases design (Appendix Figure 3).

Figure 2.

Figure 2

Open in a new tab

Summed minor allele frequency (sMAF) of risk variants in cases (solid lines) and controls (broken lines) under different study designs. We show sMAF as a function of variance of relative risk between risk variants for (a) TRAFIC, (b) the conventional case-control design, and (c) the selected cases design for summed allele frequencies (f) of 0.01, 0.05 and 0.2 and fixed mean relative risk μ = 1.15.

Power Analysis

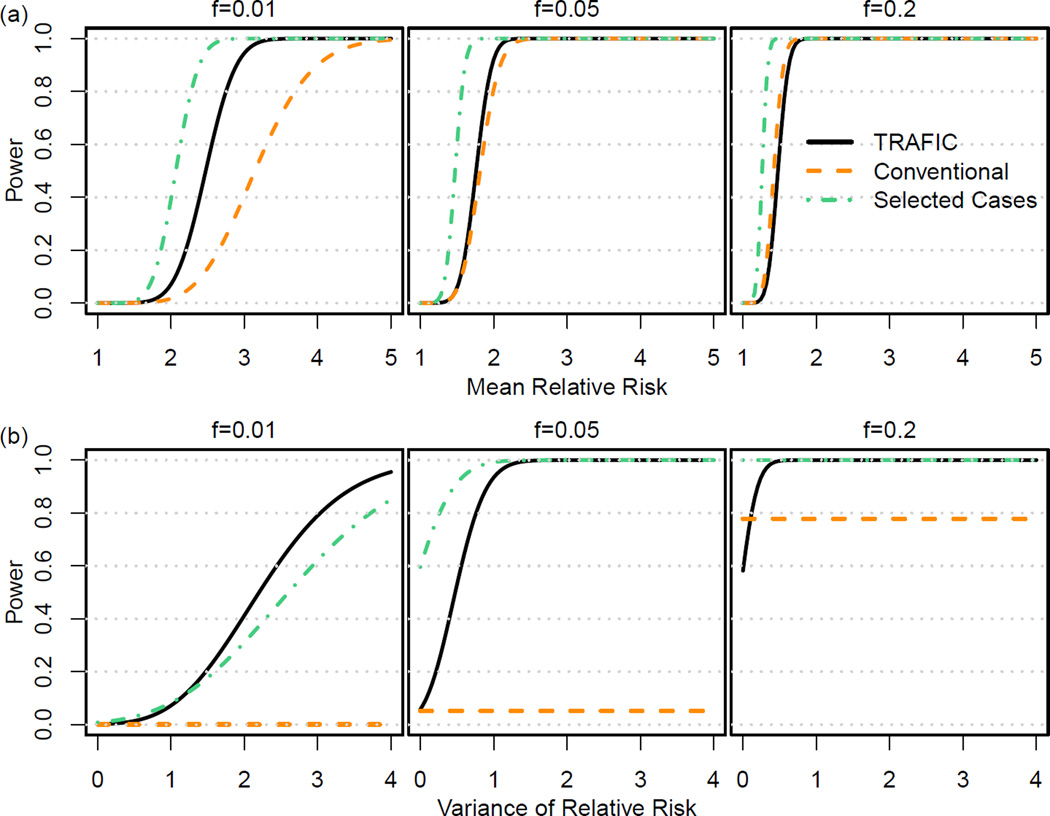
Based on the differences in expected sMAF, we calculated the analytical power for three study designs for the same number of individuals (n=2000): (1) 1000 affected sibpairs using TRAFIC, (2) 1000 cases and 1000 controls in the conventional cases-control design, and (3) 1000 cases with affected siblings and 1000 controls in the selected cases design. Thus, we generated 4000 independent observations for the conventional and the selected design, and ~3000 independent observations (~1000 cases and ~2000 controls) for TRAFIC. We also determined power empirically using simulations and observed no difference between empirical power and analytical power (Appendix Figure 4).

Assuming all risk variants had the same relative risk between 1 and 5 (σ2 = 0), the selected cases design was uniformly most powerful (Figure 3a) while the power ranking of TRAFIC and the conventional design depended on f. For rarer risk variants (f < 0.05), TRAFIC had substantially higher power than the conventional design across all relative risks analyzed. For example, for f = 0.01 and μ = 2.5, the power of the conventional design was 0.131 compared to 0.532 for TRAFIC. With increasing f or increasing prevalence, the power difference between TRAFIC and the conventional design reduced. For sets of risk variants with f > 0.05, the power of the conventional design was larger than the power of TRAFIC. For prevalence 0.20, the conventional design was already more powerful than TRAFIC for f > 0.01 (Appendix Figure 5).

Figure 3.

Figure 3

Open in a new tab

The analytical power curve for TRAFIC, conventional case-control, and selected cases design for different summed allele frequencies (f). Row (a) displays the power as a function of mean relative risk evaluated at variance of relative risk σ2 = 0. Row (b) shows the power as a function of variance of relative risk evaluated at mean relative risk μ = 1.5. Results are shown for 2000 individuals (1000 sibpairs or 1000 cases and 1000 controls) at a significance level 2.5×10−6.

For a model with allelic heterogeneity (σ2 = 0), power of TRAFIC increased with rising σ2 while the power of the conventional design was independent of σ2 and only depended on f (Figure 3b). For f = 0.01 and 0.05 at μ = 1.5, the power of TRAFIC was uniformly greater than the power of the c; = 1.5 onventional design. For f = 0.2, TRAFIC was more powerful than the conventional design forσ2 = 0.1. Even for high-prevalence diseases, TRAFIC is more powerful than the conventional design at modest levels of heterogeneity (Appendix Figure 5). Moreover, the selected cases design was no longer uniformly most powerful in the presence of moderate allelic heterogeneity. For example, when f = 0.01 and σ2 = 2, TRAFIC outperformed the selected cases design (with power of 0.412 and 0.306, respectively). For a model with no mean effect (μ = 1), TRAFIC was uniformly most powerful regardless of f (results not shown).

Population stratification

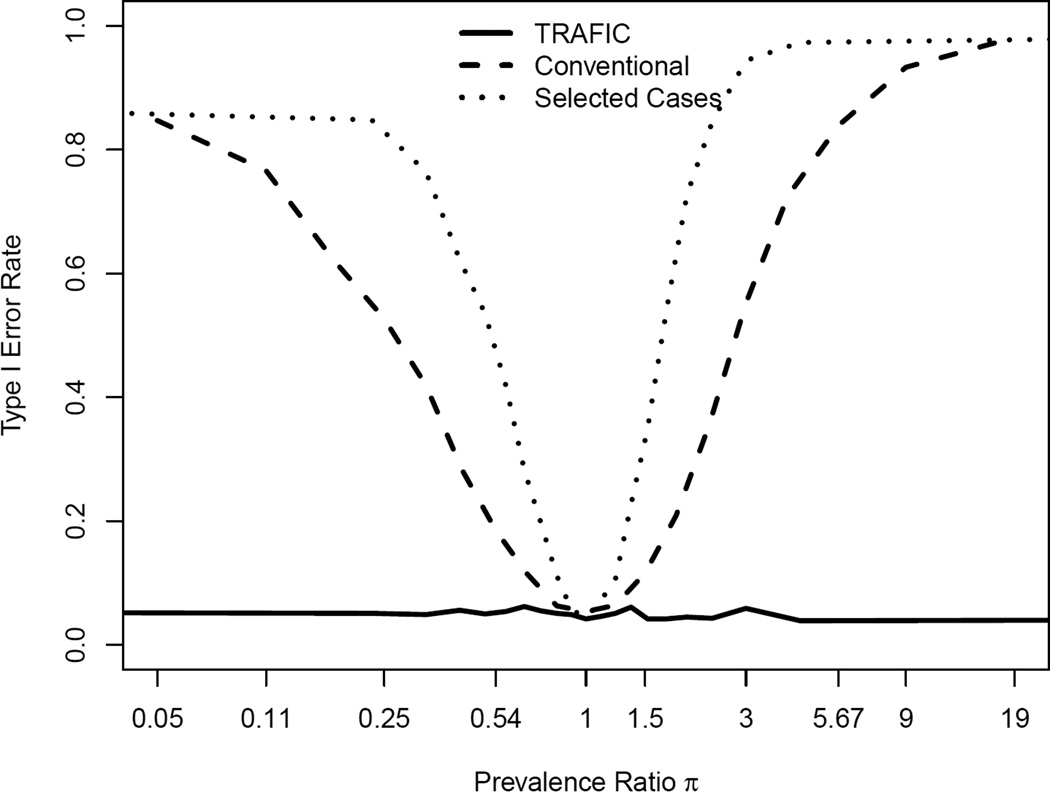
We modeled the level of population stratification by the parameter π which represents the ratio of prevalence between two populations (see methods). Under the null (μ = 1, σ2 = 0), the conventional case-control design and the selected cases design only achieved the nominal false positive rate at π =1 where equal proportion of cases and controls are sampled from the two populations. Both designs showed substantially increased false positive rate when moving away from π =1. Especially the selected cases design showed a high false positive rate for moderate levels of stratification. For π =1.22, the false positive rate was 0.064 and 0.107 for the conventional case-control and selected cases designs; the inflation increased to 0.725 and 0.973 when π = 4.06. TRAFIC maintained the false positive rate at the nominal level of 0.05 across the range of π (Figure 4) as long as we assumed either no linkage signal or a linkage signal of the same strength in the two populations. If we model a strong linkage signal in only one of the populations, we expect a slightly increased false positive rate in TRAFIC (Appendix 5).

Figure 4.

Figure 4

Open in a new tab

False positive rate in the presence for population stratification for TRAFIC, selected cases and the conventional case-control design. The false positive rate is shown as a function of the prevalence ratio π between two sampled populations. Calculations are based on a summed allele frequency of 0.01 in population 1 and 0.05 in population 2, and a sample size of 2000 individuals (1000 sibpairs or 1000 cases and 1000 controls) at a significance level 0.05.

Gene-gene interaction

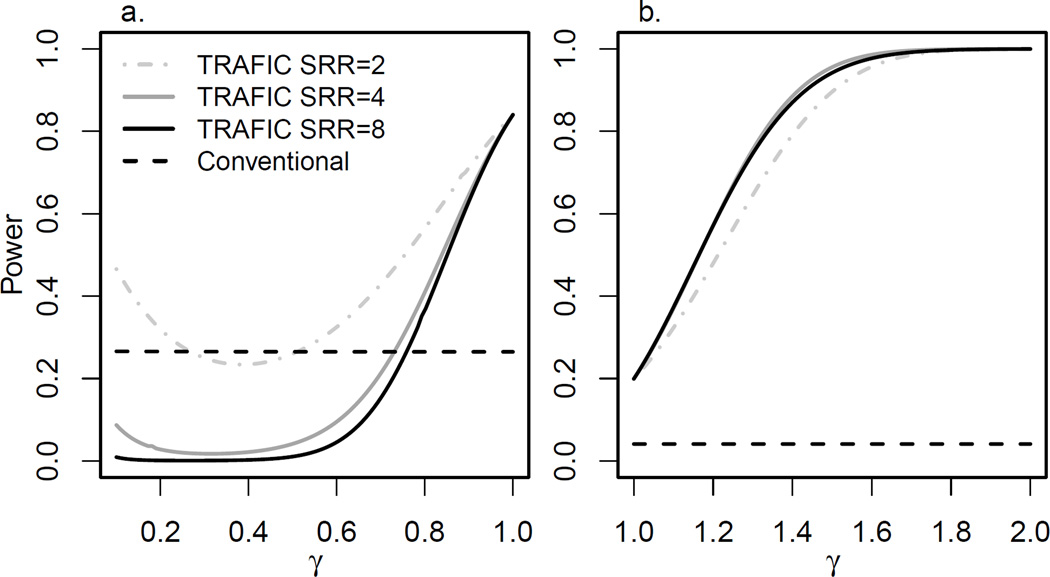
We summarized the effect of the gene-gene interaction in a two-locus model by the parameter γ (see Methods) and quantified the joint effect of both loci on the disease heritability by sibling relative risk (SRR) (see Appendix 4). To ensure comparability across values of γ, we fixed the marginal relative risk at the locus of interest, and adjusted the marginal effect at the “remaining genome” locus to maintain SRR at 2, 4 and 8. We considered a locus of interest with f = 0.01 and set the marginal relative risk to 2.2 for models with no interaction (γ = 1) or synergistic interaction (γ > 1), and to 2.8 for models with antagonistic interaction (γ < 1) to illustrate the effect of antagonistic interaction with reasonable power. The quantitative impact of interaction on power was independent of these specific parameter choices (Results not shown).

Since the marginal effect at the locus of interest was constant, the power of the conventional case-control study was not affected by the considered interaction or by SRR. The power of TRAFIC increased with γ regardless of SRR across most interaction parameters considered (Figure 5). For synergistic interaction, the power rose quickly with γ; the exact trajectory depended on SRR of the model. The power for models with a higher SRR increased faster for a lower γ, but the rate of increase also decreased faster for a higher SRR. Hence models with a lower SRR reached maximal power faster. In models of antagonistic interaction (γ < 1), TRAFIC rapidly lost power with decreasing γ. This loss of power was particularly pronounced for highly heritable disease (SRR = 8). For SRR at 2, 4, and 8, TRAFIC was less powerful than the conventional design for γ < 0.52, 0.74, and 0.76, respectively (Figure 5a). However, the power started to increase when γ < 0.38, 0.31 and 0.26 for SRR=2, 4, and 8, respectively. For this extreme model of antagonistic interaction, a variant that was causal in a population sample had a protective effect in a family sample. Hence, the minor allele frequency on shared chromosome regions became lower than the minor allele frequency on non-shared chromosome regions, generating power in a test for association.

Figure 5.

Figure 5

Open in a new tab

Analytical power of TRAFIC and the conventional case-control design under different models of gene-gene interaction. The horizontal axis displays the interaction parameter γ; gray and black lines represent different overall heritability parameterized as sibling relative risk (SRR). Panel a represents the result for antagonistic interaction (γ < 1); panel b represents the result of synergistic interaction (γ > 1). Results are shown for 2000 individuals (1000 sibpairs or 1000 cases and 1000 controls) at a significance level 2.5×10−6.

Discussion

We introduce a new framework for gene-based association tests of rare variants leveraging affected sibpairs (TRAFIC). We compare the number of risk alleles located on chromosome regions shared IBD in an affected sibpair to the number of risk alleles located on chromosome regions that are not shared IBD. TRAFIC compares "cases" and "controls" within a sibpair as a matched design and is thus generally robust to population stratification. The test evaluates the null hypothesis of no association and can therefore generate a signal only in the presence of association and is powerful in the absence of linkage.

The proposed design of taking shared chromosome regions as new “cases” and non-shared chromosome regions as new “controls” can be applied to any published gene-based test. In this study, we evaluated the design for a collapsing gene-based test as the power of this test can be calculated without specifying minor allele frequency or effect size distribution of each risk variant, and it is therefore easier to obtain general conclusions. However, TRAFIC can also be applied to dispersion tests such as SKAT [Wu et al., 2011].

We calculate the power of this new method using a general model for risk variants, which is specified by the summed allele frequency of risk variants, and mean and variance of relative risk for risk variants. We compared three study designs: (1) TRAFIC, (2) the conventional design of cases and controls, and (3) a design where cases are enriched for rare variants by selecting case individuals with affected relatives assuming the same number of sequenced/genotyped samples. For diseases with prevalence ~1% and in the absence of gene-gene interaction, TRAFIC was more powerful than the conventional case-control design for variants with summed risk allele frequency less than 0.05, even though the conventional case-control design contained more independent observations. This power gain has two drivers. First, families ascertained to carry multiple affected individuals are more likely to segregate risk variants than random cases [Fingerlin, Boehnke and Abecasis, 2004, Peng et al., 2010, Zöllner, 2012]. Second, if such risk variants are rare, the founders of the pedigree are likely to only carry one copy. As the probability of carrying the risk variant is increased for each affected family member, this variant is more likely to be located on a shared chromosome. With increasing allelic heterogeneity, the probability for both affected siblings sharing an allele with a large effect size also rises, increasing the number of risk alleles located on shared IBD chromosome regions. Hence in the presence of allelic heterogeneity, the power of TRAFIC increased, while the power of the conventional case-control design was unchanged.

The power of a family-based design also depends on the interaction between variants at the locus of interest and the remaining genome. Sampling from families with multiple affected individuals increases the overall genetic load for all cases. Hence, if the genetic effect at the locus of interest increases with overall genetic load, the power advantage of family-based designs over population-based designs is larger than under a model of no interaction. On the other hand, if the genetic effect of risk variants at the locus of interest decreases with overall genetic load, the power in family-based designs is smaller than the power under a model of no interaction and population-based designs can be more powerful. This effect has been described before for additive gene-gene interaction, which is a special case of genetic effect at the locus of interest decreasing with overall genetic load [Risch N, 2001, Ionita-Laza and Ottman, 2011, Zöllner, 2012, Helbig, Hodge and Ottman, 2013].

Moreover, TRAFFIC is generally robust to population stratification, as it compares IBD chromosome regions to non-chromosome regions in every sibpair thus naturally matching the genetic background of samples. This robustness can be violated in regions where one of the populations has a strong linkage signal while the other population has no evidence for linkage. However, this unlikely scenario only results in minor increase of the false positive rate and has thus little impact on the utility of our method. As the efficacy of current methods to control for population stratification in population based designs for rare variant tests is not clear [Mathieson and McVean, 2012, Liu, Nicolae and Chen, 2013], family based designs may be necessary to avoid spurious association. TRAFIC achieves this robustness to stratification by using non-shared chromosomes as controls at the cost of some reduction in power. As non-shared chromosomes have a higher risk allele frequency than chromosomes in population controls, a test comparing shared chromosomes against chromosomes from unaffected controls may be more powerful than TRAFIC. However, such a design would be very susceptible to population stratification, even more than the selected cases design shown in figure 4.

In conclusion, we have proposed TRAFIC using affected sibpairs for testing the association between a set of rare variants and the disease phenotype. TRAFIC is more powerful than the conventional case-control design under a wide range of models while being generally robust to population stratification.

Supplementary Material

Supp AppendixS1

Acknowledgments

The authors thank Goncalo Abecasis, Michael Boehnke, and Trivellore Raghunathan for helpful discussions. This work was supported by National Institutes of Health grant HG005855.

Footnotes

Web Resources

The R code and manual for TRAFIC can be downloaded from http://www-personal.umich.edu/~khlin/.

References

  1. Chen H, Meigs JB, Dupuis J. Sequence kernel association test for quantitative traits in family samples. Genet Epidemiol. 2013;37:196. doi: 10.1002/gepi.21703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Cooper GM, Shendure J. Needles in stacks of needles: finding disease-causal variants in a wealth of genomic data. Nat Rev Genet. 2011;12:628. doi: 10.1038/nrg3046. [DOI] [PubMed] [Google Scholar]
  3. De G, Yip W, Ionita-Laza I, Laird N. Rare variant analysis for family-based design. PloS One. 2013;8:e48495. doi: 10.1371/journal.pone.0048495. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
  5. Fang S, Sha Q, Zhang S. Two adaptive weighting methods to test for rare variant associations in family-based designs. Genet Epidemiol. 2012;36:499. doi: 10.1002/gepi.21646. [DOI] [PubMed] [Google Scholar]
  6. Fingerlin TE, Boehnke M, Abecasis GR. Increasing the Power and Efficiency of Disease-Marker Case-Control Association Studies through Use of Allele-Sharing Information. The American Journal of Human Genetics. 2004;74:432. doi: 10.1086/381652. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Guan W, Boehnke M, Pluzhnikov A, Cox NJ, Scott LJ. Identifying Plausible Genetic Models Based on Association and Linkage Results: Application to Type 2 Diabetes. Genet Epidemiol. 2012;36:820. doi: 10.1002/gepi.21668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Guo W, Shugart YY. Detecting rare variants for quantitative traits using nuclear families. Hum Hered. 2012;73:148. doi: 10.1159/000338439. [DOI] [PubMed] [Google Scholar]
  9. Helbig I, Hodge SE, Ottman R. Familial cosegregation of rare genetic variants with disease in complex disorders. European Journal of Human Genetics : EJHG. 2013;21:444. doi: 10.1038/ejhg.2012.194. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Howson JMM, Walker NM, Clayton D, Todd JA. Confirmation of HLA class II independent type 1 diabetes associations in the major histocompatibility complex including HLA-B and HLA-A. Diabetes Obes Metab. 2009;11(Suppl 1):31. doi: 10.1111/j.1463-1326.2008.01001.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ionita-Laza I, Ottman R. Study designs for identification of rare disease variants in complex diseases: the utility of family-based designs. Genetics. 2011;189:1061. doi: 10.1534/genetics.111.131813. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Keith JM, McRae A, Duffy D, Mengersen K, Visscher PM. Calculation of IBD probabilities with dense SNP or sequence data. Genet Epidemiol. 2008;32:513. doi: 10.1002/gepi.20324. [DOI] [PubMed] [Google Scholar]
  13. Laird NM, Lange C. Family-based designs in the age of large-scale gene-association studies. Nat Rev Genet. 2006;7:385. doi: 10.1038/nrg1839. [DOI] [PubMed] [Google Scholar]
  14. Li B, Leal SM. Methods for Detecting Associations with Rare Variants for Common Diseases: Application to Analysis of Sequence Data. Am J Hum Genet. 2008;83:311. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Liu Q, Nicolae DL, Chen LS. Marbled inflation from population structure in gene-based association studies with rare variants. Genet Epidemiol. 2013;37:286. doi: 10.1002/gepi.21714. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Mardis E, Chakravarti A, Valle D, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mathieson I, McVean G. Differential confounding of rare and common variants in spatially structured populations. Nat Genet. 2012;44:243. doi: 10.1038/ng.1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Nelson MR, Wegmann D, Ehm MG, et al. An abundance of rare functional variants in 202 drug target genes sequenced in 14,002 people. Science. 2012;337:100. doi: 10.1126/science.1217876. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Peng B, Li B, Han Y, Amos CI. Power analysis for case-control association studies of samples with known family histories. Hum Genet. 2010;127:699. doi: 10.1007/s00439-010-0824-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Price AL, Kryukov GV, de Bakker PIW, et al. Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet. 2010;86:832. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
  22. Rao DC, Province MA, Leppert MF, et al. A genome-wide affected sibpair linkage analysis of hypertension: the HyperGEN network. American Journal of Hypertension. 2003;16:148. doi: 10.1016/s0895-7061(02)03247-8. [DOI] [PubMed] [Google Scholar]
  23. Risch N. Implications of Multilocus Inheritance for Gene-Disease Association Studies. Theor Popul Biol. 2001;60:215. doi: 10.1006/tpbi.2001.1538. [DOI] [PubMed] [Google Scholar]
  24. Risch N. Linkage strategies for genetically complex traits. I. Multilocus models. Am J Hum Genet. 1990;46:222. [PMC free article] [PubMed] [Google Scholar]
  25. Schaffner SF, Foo C, Gabriel S, Reich D, Daly MJ, Altshuler D. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 2005;15:1576. doi: 10.1101/gr.3709305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Schifano ED, Epstein MP, Bielak LF, et al. SNP Set Association Analysis for Familial Data. Genet Epidemiol. 2012;36:797. doi: 10.1002/gepi.21676. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Shugart YY, Zhu Y, Guo W, Xiong M. Weighted pedigree-based statistics for testing the association of rare variants. BMC Genomics. 2012;13:667. doi: 10.1186/1471-2164-13-667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Tabor HK, Jabs EW, Buckingham KJ, et al. Exome sequencing identifies the cause of a mendelian disorder. Nat Genet. 2010;42:30. doi: 10.1038/ng.499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wong M, Eichler EE, Shaffer T, et al. Targeted capture and massively parallel sequencing of 12 human exomes. Nature. 2009;461:272. doi: 10.1038/nature08250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet. 2011;89:82. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Zawistowski M, Gopalakrishnan S, Ding J, Li Y, Grimm S, Zöllner S. Extending Rare-Variant Testing Strategies: Analysis of Noncoding Sequence and Imputed Genotypes. Am J Hum Genet. 2010;87:604. doi: 10.1016/j.ajhg.2010.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Zöllner S. Sampling strategies for rare variant tests in case-control studies. Eur J Hum Genet. 2012;20:1085. doi: 10.1038/ejhg.2012.58. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp AppendixS1
NIHMS681495-supplement-Supp_AppendixS1.docx (184.7KB, docx)

RESOURCES