Populations adapt to fluctuating selection using derived and ancestral allelic diversity

Abstract

Populations can adapt to changing environments by using allelic diversity, yet whether diversity is recently derived or ancestral is often debated. While evolution could productively use both types of diversity in a changing environment, their relative frequency has not been quantified. We address this question experimentally using budding yeast strains that harbor a tandem repeat-containing URA3 gene, which we expose to cyclical selection and counter-selection. We characterize and quantify the dynamics of frameshift events in the URA3 gene in eight populations over twelve cycles of selection and find that ancestral alleles account for 10 – 20% of all adaptive events. Using a general model of fluctuating selection, we determine how these results depend on mutation rates, population sizes, and fluctuation timescales. We quantify the contribution of derived alleles to the adaptation process using the de novo mutation rate along the population’s ancestral lineage, a novel measure that is applicable in a wide range of settings. We find that the adaptive dynamics undergoes a sharp transition from selection on ancestral alleles to selection on derived alleles as fluctuation timescales increase. Our results demonstrate that fluctuations can select between different modes of adaptation over evolutionary timescales.

Introduction

Environments in nature are rarely constant. Populations must survive over different timescales of environmental changes, from as short as transient nutrient fluctuations to as long as global climatic change. Understanding evolutionary strategies in fluctuating environments, and their genetic mechanisms, is critical for explaining and predicting adaptive changes. Population genetics data are revealing in increasing detail the genetic diversity in nature, yet numerous debates on evolutionary mechanisms persist. In particular, the role of environmental changes in evolutionary dynamics and their impact on genetic diversity remain poorly understood. While the timescales of environmental changes might be very fast on an evolutionary scale – e.g. a few years or a few decades – from an experimental standpoint such timescales are almost prohibitively long for an extensive study. Laboratory evolution experiments provide unique insights into aspects of evolution that are difficult to observe directly in nature (Woods et al. 2011; Dai et al. 2012; Hekstra and Leibler 2012; Meyer et al. 2012). While most evolution experiments have been performed under relatively constant conditions (Kawecki et al. 2012; Kussell 2013), a small number have studied evolution under fluctuating selection (Beaumont et al. 2009; Hallsson and Bjorklund 2012; Quan et al. 2012; New et al. 2014).

Stochastic switches based on tandem repeat (TR) variation – which are hotspots for reversible insertion-deletion mutations, or indels (Verstrepen et al. 2005; Moxon et al. 2006; Orsi et al. 2010; Bayliss and Palmer 2012) – provide a possible mechanism for adaptation to fluctuating environments (Koch 2004; Wernegreen et al. 2009). These mechanisms can be studied by laboratory experiments due to their fast timescales, however their population dynamics have not been extensively studied before. Well-known examples involve phase-variation genes, or contigency loci, such as hmbR in Neisseria meningitidis, where a polyG repeat tract acts as a hotspot for frameshift mutations that cause reversible phenotypic switching (Richardson and Stojiljkovic 1999). Other examples are found in budding yeast Saccharomyces cerevisiae, where indels that occur within TRs in promoter regions alter the expression level of downstream genes (Vinces et al. 2009).

To quantify adaptive dynamics in a stochastic switching population, we used an S. cerevisiae strain with a genetically engineered TR within the URA3 coding sequence (Verstrepen et al. 2005; Legendre et al. 2007). We study population dynamics under fluctuating selection in cycling environments: selecting for URA3⁺ and counter-selecting for URA3⁻. The TR enables rapid, reversible switching between URA3⁺ and URA3⁻ by generating frameshift mutations at high frequency. We propagate eight independent populations on plates through twelve selection-counter-selection cycles, and measure changes in TR size at each time point. Using theory and simulations we model the data, and show that the experimental populations survive by using a mixture of two distinct adaptive mechanisms. We provide a theoretical framework that precisely quantifies this result, and can be flexibly applied in many other contexts.

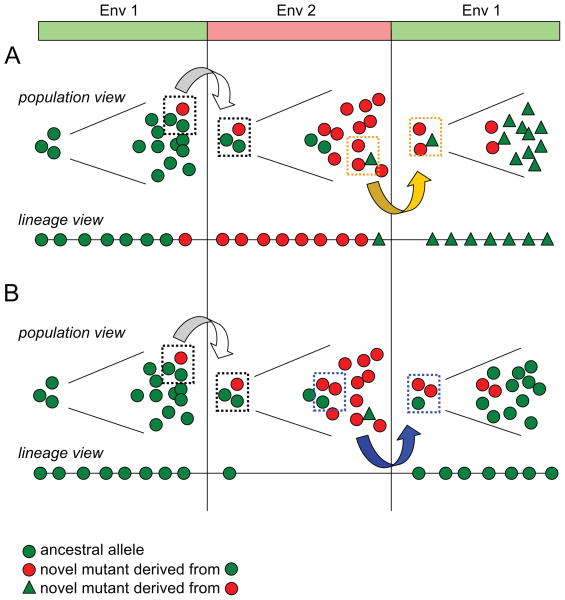
To illustrate the two adaptive mechanisms, we present a schematic in Fig. 1 of a heterogeneous population growing in a periodically alternating environment, with two different phenotypes adapted to two different environments. At each environmental change, the population goes through a bottleneck. Two scenarios are shown, which differ only by the random choice of individuals that survive the bottleneck, and exhibit nearly identical dynamics at the population level. However, if we randomly pick one individual and track its ancestral lineage backward, the dominant ancestral lineages reveal a clear difference between the two mechanisms.

Figure 1. Schematic of evolutionary dynamics with fluctuating selection.

Cells within a population can mutate between two states, represented as green (adapted to environment 1) and red (adapted to environment 2). Population bottlenecks occur during the environmental changes, and only a fraction of cells (indicated as dashed squares) are passaged to the next environment. In environment 2, two non-adaptive alleles, differing in origin, coexist: the green circles represent a residual subpopulation which originated from the previous episode, while the green triangles represent novel mutants derived from red individuals. The lineage view shows the phenotypic state of each ancestral cell along a lineage of a single surviving cell at the end of the experiment. Depending on the composition of the bottleneck, the population adapts by the derived allele mechanism (A) or the ancestral allele mechanism (B). Note that in (B), during the expansion of the red phenotype in environment 2, the ancestral cell along the lineage is non-adaptive (green) hence it does not divide, as indicated by a single circle on the lineage in environment 2.

In the Fig. 1A, we show a scenario in which for each subsequent environmental episode, the majority allele (green circle, red circle, green triangle) is a new mutation derived from the previously dominant allele. We refer to this as the derived allele mechanism, since the selected alleles that appear in the ancestral lineage consist of a new mutation at each environmental change. Specifically, going backward in time, all green individuals coalesce onto the background of a red individual from environment 2, then all red individuals in environment 2 coalesce onto a green individual from the original environment 1. In Fig. 1B, we present a case in which a single allele (green circle) rises to high frequency in the 1^st and 3^rd environmental episodes, while a different allele (red circle) becomes a majority in the second episode. We refer to this as the ancestral allele mechanism, since the selected alleles that appear in the ancestral lineage persist through multiple environmental changes. That is, going backward in time, all green individuals coalesce onto a green individual from environment 2 which was sampled from the original environment 1.

Several studies have previously analyzed selective sweeps from standing variation versus from de novo mutations (Hermisson and Pennings 2005; Przeworski et al. 2005; Pennings and Hermisson 2006; Peter et al. 2012). In those analyses, a major question was whether alleles were already in existence before a specific time point, e.g. an abrupt change of environment, or were formed de novo after the change. These distinctions are useful when environmental changes are rare and abrupt. However, they become less meaningful when environments change frequently (as in our experiments) or in a continuous manner. For this reason, in our theoretical analysis we focus on the rate at which new alleles occur along the ancestral lineage, which is a general measure that operates robustly in all contexts.

Population genetics data indicates that selective sweeps from standing variation make up a significant percentage of recent adaptations in flies and humans (Burke et al. 2010; Pritchard et al. 2010; Hernandez et al. 2011). While statistical methods have been developed to identify the signatures of sweeps from standing variation versus de novo mutation in molecular sequence data (Peter et al. 2012), the role of environmental changes and their timescales is rarely considered. Our work presents a model experimental system in which both types of mechanisms are shown to contribute to adaptation in a fluctuating environment. Using theoretical analysis, we demonstrate that the dynamics transitions from selection on ancestral alleles to selection on recently derived alleles over a relatively narrow range in parameter space, including mutation rates, population sizes, and fluctuation timescales.

Materials and methods

The full materials and methods of the experiment are described in Supporting Information.

Results

Tandem repeats within coding regions facilitate survival under fluctuating selection

We used the yeast strains KV948 and KV653 (Verstrepen lab) which have a genetically altered URA3 gene with a TR consisting of (AC)-repeats in the coding region immediately after the ATG start site (Fig. S1A), which translate into His-Ile repeats. The KV948 strain (‘short-TR strain’) has (AC)-repeats with 7.5 units (15 bp). The KV653 strain originally had (AC)-repeats with approximately 68 units. At the start of the evolution experiment, the strain derived from KV653 had 50 (AC)-repeat units (‘long-TR strain’).

The URA3 gene encoding orotidine-5′-phophate decarboxylase is a standard yeast genetic marker subject to selection (in the absence of uracil) and counter-selection (by adding 5-FOA which is converted into a toxic compound by URA3) (Boeke et al. 1984). Cells that survive in the selective medium should have a functional, in-frame URA3 gene (the ON state), while survivors in the counter-selective medium should have a non-functional URA3 (the OFF state). The long-TR strain has a significantly higher phenotypic mutation rate in the URA3 gene (Table S1) due to frameshift mutations in the TR region.

We performed fluctuating selection on both short- and long-TR strains. Yeast colonies were passaged through alternate SC-ura (selective) and SC+5FOA (counter-selective) plates (Fig. S1B). At each passage, a single colony (~ 10⁵ cells) was picked and dispersed by streaking on a plate with opposite selective pressure. Only a few mutants survived and formed colonies in the new environment. These colonies could form anywhere along the streak, and therefore could contain more than one founder cell. The number of founders, n, is the bottleneck size, a quantity that varies randomly depending on the location of the mutant along the streak. Based on colony area and number of cells, we estimate that n could range from 1 – 400 cells.

The short-TR strain (initially ON) went extinct after being spread on the first counter-selective plates (4 independent passages). In contrast, the long-TR strain (initially OFF) survived for multiple selective/counter-selective cycles, and was therefore used for longer term experiments with 8 populations (A1~A4, B1~B4) passed through 12 selective/counter-selective cycles. Evolutionary trajectories of each lineage are shown in Figs. 2 & S2. We observed seven extinction events (Figs. 2B & S2B, red marks), corresponding to extinction probabilities of 4/96 (selection->counter-selection) and 3/96 (counter-selection->selection); these two values were not statistically different (Fisher exact test, p>0.1). Each time extinction occurred, a colony from a parallel lineage was used to replace the extinct lineage, resulting in occasional branching of the lineages.

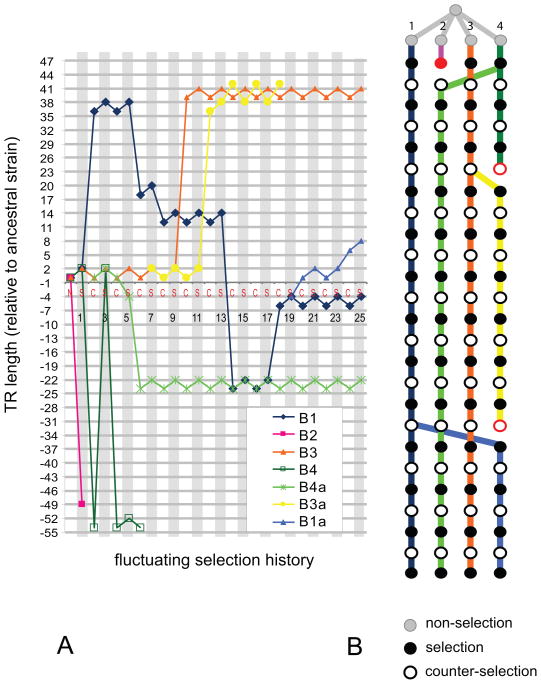
Figure 2. Evolutionary trajectories of the B-lineages.

(A) Evolutionary trajectory of the B-lineages. The horizontal axis represents passages, and the vertical axis represents TR length (in bp) relative to the ancestral genotype. The horizontal gray lines correspond to in-frame TR lengths, and the vertical gray strips correspond to the selective environment.

(B) Lineage representation of the B-lineages. The color of each lineage corresponds to the color in (A). Gray, black, and white nodes represent non-selective, selective, and counter-selective environments. Nodes shown in red are the last node in each lineage, followed by extinction events.

Phenotypic switching is caused by indels within the TR locus

Populations after each passage are represented as circles in Figs. 2B & S2B, which we refer to as nodes. We genotyped each node by amplifying the flanking region around the TR in URA3 by PCR, and using DNA fragment analysis to determine the number of repeat units in TRs (Materials & Methods). The error-prone nature of long repetitive sequences makes this locus difficult to sequence by Sanger sequencing. Since the point mutation rate in the URA3 gene (3.8 × 10⁻¹⁰ per bp (Lang and Murray 2008)) is orders of magnitude lower than the indel rate in the TR (see below), determining the length of the TR was sufficient for our analysis. By aligning the DNA fragment analysis raw data from adjacent nodes, we could accurately determine the TR length differences (Materials & Methods), and reconstruct the insertion/deletion history for all lineages (Figs. 2 & S2). As a control, we performed a neutral selection experiment: colonies of the long-TR strain were passaged through 25 SC plates with no selective pressure, and exhibited zero TR length differences during 25 passages for two genotyped lineages.

In all cases, the coding frames determined by the indel size agreed with selection type: the selective episode (vertical gray shade in Figs. 2A & S2A) always yielded an in-frame URA3 (horizontal gray line in Figs. 2A & S2A), while the counter-selective episode always yielded a frame-shifted URA3. When large indels occurred (length difference > 4), we could only determine the TR size with ±2 bp accuracy, and therefore could not confidently determine the frame. However, we were always able to find a consistent frame that fits all subsequent episodes and TR lengths after large indel events.

Unexpected fitness difference between two OFF frames

Depending on the length of the TR sequence, the coding region after the (AC)_n repeat can have three difference frames (Fig. S4):

1. If the TR has 3m bp length (m is an integer), the coding region encodes a functional URA3 and we call these alleles the ON frame alleles.

2. If the TR has 3m-2 bp length, the coding region after the TR encodes a 4 a.a. peptide, and we call these alleles the (−2)OFF frame alleles.

3. If the TR has 3m+2 bp length, the coding region after the TR encodes a 45 a.a. peptide with no known homology, and we call there alleles as (+2)OFF frame alleles.

The (−2)OFF or (+2)OFF frames can be obtained, respectively, by a 2-bp deletion or 2-bp insertion from the ON frame; or alternatively by larger insertions or deletions. Across the 8 evolved lineages, which started from an ancestral (−2)OFF allele, we obtained 32 different alleles that represent all three different frames above. Surprisingly, the two OFF frames appear highly asymmetrically in the experiment: there are 16 alleles belonging to the (−2)OFF frame, while only one allele belongs to the (+2)OFF frame. Furthermore, for all large indels (> 6 bp) that result in a phenotypic switch from the ON frame, all of them (12/12) mutated into (−2)OFF frames. Molecularly, there is no known mechanism by which these large indel mutations could distinguish between the two types of OFF frames. Therefore, we tested whether there exists a selective difference between the two OFF frames.

The two alleles for (+2)OFF frames were obtained from the A3 (node #5) and A4 (node #5) lineages, and both were 4 bp longer than the ancestral strain. We chose another two alleles in the (−2)OFF frame in the same lineages, the A3 (node #3) and A4 (node #3), for comparison. For both OFF frames, evolved yeast strains had similar growth rate in SC medium (see Table S2). However, in SC+5FOA medium, the (+2)OFF frame strains have approximately 50% growth rate reduction relative to (−2)OFF frame strains (see Table S2). This result explains why the (+2)OFF frame is rare: the colony sizes of (+2)OFF frame are much smaller than (−2)OFF frame (Fig. S4) after 48 hr incubation, and may not yet be visible, hence they are unlikely to be picked during the colony passages. Therefore, even though the growth rate is only 50% reduced, the number of (+2)OFF colonies passaged to the next episode is very small. This effect would be even more pronounced in liquid culture, as the ratio of the numbers of cells in the (−2)OFF frame to the (+2)OFF frame grows exponentially with time. The mechanistic basis for the toxicity of the (+2)OFF frame peptide is unknown. Since the peptide is highly hydrophobic, we speculate it may be related to the unfolded protein response.

Indel mutation spectrum and mutation rates in the TR locus

We observed a large number of indel events over the entire experiment, which we used to infer the TR’s indel mutational spectrum. However, the frequency statistics do not simply measure the mutational spectrum for two reasons: (1) The observed mutant alleles are selected to enable cellular growth in the new environment; indel mutations that generate a non-adaptive phenotype do not survive, and cannot be detected. (2) Some of the TR length changes could be due to selection on standing diversity, and may not represent novel mutations. We account for these effects as follows. First, by restricting our statistics to the adaptive alleles in each environment, we infer the relative mutational rates among these alleles. Second, although some of the TR size changes may not be new mutations, whenever a new length occurs in the lineage it must correspond to a novel indel mutation. The statistical analysis was therefore performed in two limits: either according to maximum parsimony (counting only new TR sizes along each lineage), or according to maximum novelty (counting each TR length change as a new mutation). The true mutational spectrum lies between these two extremes.

We found a total of 95 TR length changes from the URA3 ON frame to the (−2)OFF frame. The indel size spectra were determined by maximum novelty (Fig. 3A, blue bars) and maximum parsimony (Fig. 3A, purple bars). We found that small indels (< 6 bp) are much more frequent than large indels (> 6 bp). Furthermore, small indels are always multiples of 2 bp. This is consistent with the nature of dimeric repeats in which indels are favored to occur in repeat units due to the slipped-strand mispairing mechanism (Hite et al. 1996). For large indels, we found cases with an odd number of basepairs, indicating that small and large indels could be governed by different molecular mechanisms. The mutational spectrum of the URA3 (−2)OFF frame to ON frame reveals similar conclusions (Fig. 3B), except that much fewer large indels occur in these selective episodes. The occurrence of large indels under the 5-FOA-based counter-selection may be due to the toxic effects of the drug.

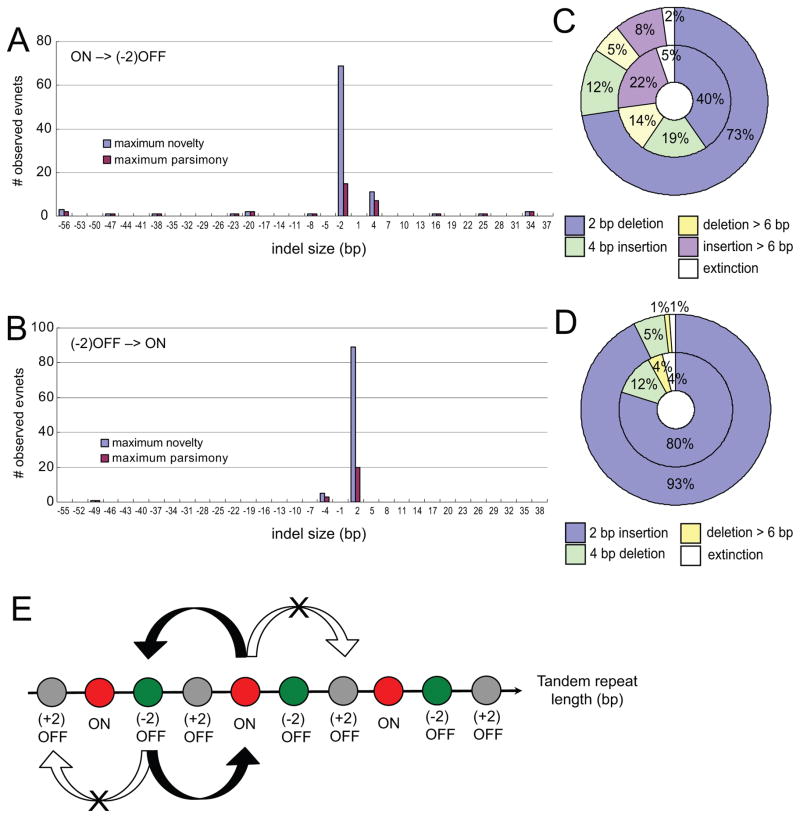
Figure 3. Mutational spectrum and trajectory in fluctuating selection.

(A) Mutational spectrum of all ON –> (−2)OFF mutation events.

(B) Mutational spectrum of all (−2)OFF –> ON mutation events.

(C) Frequency of different indel types shown in (A). Inner ring: maximum parsimony. Outer ring: maximum novelty.

(D) Frequency of different indel types shown in (B). Inner ring: maximum parsimony. Outer ring: maximum novelty.

(E) Mutational trajectory for 2 bp TR length oscillations. Each circle represents a TR length. Different frames are indicated in different color, and the black arrows represent the commonly observed 2 bp length oscillation seen in the experiment. White arrows represent alternative mutations that cannot survive in fluctuating selection.

We measured the indel mutation rates using fluctuation analysis (Materials & Methods). The long-TR strain had indel rates of ~10⁻⁴ per generation (OFF->ON selection) and 5×10⁻⁵ per generation (ON->OFF counter-selection); the mutation rate of the short-TR strain (OFF->ON selection) is ~10⁻⁸ per generation (Table S1). Since the number of mutants used in the fluctuation analysis is measured by counting surviving colonies, it is affected by the stringency of the selective/counter-selective media. In counter-selection (SC+5FOA medium), all URA3⁺ cells experience growth arrest since the toxic product 5-FU blocks the cell cycle (Seiple et al. 2006). Furthermore, for some URA3⁻ cells that mutated just before the passage, residual URA3 protein within the cytoplasm would also cause cell cycle arrest. Since a fraction of genetically URA3⁻ cells can exhibit a URA3⁺ phenotype, their number during counter-selection is underestimated. Thus, we expect the actual mutation rate to be between 2×10⁻⁴ – 5×10⁻⁵ per generation.

Since the population size of a single yeast colony is ~10⁵ cells, these measurements predict that only the long-TR strain would generate sufficient numbers of novel mutants to survive over multiple selective episodes, consistent with our results. To test whether there is an insertion vs. deletion bias for 2 bp indels, we measured the mutation rate from (−2)OFF -> ON (typically a 2 bp insertion) and from (+2)OFF -> ON (typically a 2 bp deletion). We observed no significant difference between the rates (Table S1, Lineage A4, 3^rd and 5^th nodes).

TR length oscillations under fluctuating selection

In many of the evolved lineages, two different TR lengths occur repetitively in adjacent nodes. For example, the B3 lineage (orange line in Fig. 2A) has alleles with TR length 39 and 41 bp (relative to the ancestral length) which occur recurrently in nodes 10–25. We call this behavior a TR length oscillation. We observed 2 bp length oscillations in most of the lineages (26 cases in total). 4 bp length oscillations occurred in lineages B3a and A1c. One case of a 56 bp length oscillation was seen in lineage B4.

As discussed in the Introduction, the length oscillation behavior could be due to either ancestral or derived allele mechanisms. The ancestral allele mechanism, which adapts using preexisting diversity, is sensitive to the bottleneck size (n) during the colony passage process. If n is too small, the ancestral allele is more likely to be lost by chance during passage, and this mechanism is less likely to support population adaptation. At each passage, the original population is dispersed into thousands of microcolonies. Within each microcolony, most of the ~n cells are adapted to the previous environment, while there may be a small number (~1) of mutant cells adapted to the new environment, which grow and expand to form a macroscopic colony of size N ~ 10⁵ cells. The new colony contains ~n residual cells with the ancestral genotype, which can proliferate in the next round to form new colonies. Based on the sector area streaked (~250 mm²), we estimate the upper bound on n ~ 400 cells, noting that n is expected to be lower than 400 since not all residual cells are transferred at each passage – most do not divide when the colony is growing hence may remain at the bottom of the colony or lose viability.

Alternatively, in the derived allele mechanism, new mutants arise with different indel sizes yielding adaptive alleles in the population. In this case, a k-cycle TR oscillation requires 2k successive mutations with identical indel sizes. The total likelihood of having a k-cycle TR oscillation using novel mutations is the joint probability of 2k insertions/deletions in an alternating order. For TR oscillations of 2 bp, which are the most common type (black trajectory in Fig. 3E), we note that a 2 bp deletion from ON yields a (−2)OFF frame while a 2 bp insertion yields a (+2)OFF frame. Since the latter has lower fitness in SC+5FOA medium, the 2 bp deletion is preferentially selected. A further 2 bp deletion would generate another OFF frame, which does not change phenotype, hence a 2 bp insertion is again preferentially selected, regenerating the original allele. Together, the frame structure and the fitness bias toward (−2)OFF frames enables the 2 bp TR length oscillation. However, due to the prevalence of 2 bp indels, the above explanation does not hold for the 4 bp and 56 bp TR oscillations observed in the experiment. These larger indel oscillations have a much higher probability to be disrupted either by 2 bp indels or by other large indels with a different size. As our detailed analysis in the next section shows, the large indel oscillation events are likely due to selection on standing diversity.

TR oscillation length distributions indicate a mixture of adaptive mechanisms

To determine whether the diverse durations of oscillations (Figs. 2 & S2) can be explained by the derived allele mechanism alone, we analyzed their distribution. The probability q of a single cycle of a 2 bp oscillation between ON and (−2)OFF (black trajectory in Fig. 3E) is given by

$$q=Pr\{2\text{bp}\text{deletion}|\text{starting}\text{from}\text{ON}\}\times Pr\{2\text{bp}\text{insertion}|\text{starting}\text{from}(-2)\text{OFF}\}.$$ (1)

Intuitively, if q is close to 1, then the black trajectory in Fig. 3E is likely to happen and we have a higher chance to observe a TR length oscillation over multiple cycles. If q is close to 0, a single cycle is unlikely, and the lineage is more likely to either survive by a different mutational trajectory (e.g. using large indels) or to go extinct. Since indel events along the evolutionary history are independent, the probability to observe k periods follows the geometric distribution, q^k(1-q), and the mean number of oscillation periods is q/(1-q).

We applied a maximum likelihood method on all 2-bp TR-oscillation tracks (see Materials and Methods) and estimated the parameter q = 0.74, with a 90% confidence interval given by [0.61, 0.86]. Likewise, q can also be independently estimated based on the indel mutational spectrum. We estimated q from data (Fig. 3C, D) using the two different mutational spectra. We find Pr{2bp deletion|starting from ON} = 40% (maximum parsimony) or 73% (maximum novelty), and Pr{2bp insertion|starting from (−2)OFF} = 80% (maximum parsimony) or 93% (maximum novelty). Substituting into equation (1), the estimated range of the parameter q is 0.32 – 0.68.

While the upper estimate of q based on the mutational spectrum (0.68) is well below the maximal likelihood value (0.74), the wide confidence interval suggests that the 2 bp indel data alone could be consistent with the exclusive derived allele mechanism. However, this is not the case for the larger indel data: the 4 bp and 56 bp TR oscillations are clearly inconsistent with this mechanism. The 56 bp oscillation is in all likelihood due to an ancestral allele, since otherwise it would require a 56 bp deletion to be followed by an insertion of precisely the same size (rather than any other length or much more probably a 2 bp indel). From the mutation spectrum data we infer that a single 4 bp insertion has probability at most 0.2, and a single 4 bp deletion has probability at most 0.12. Therefore, a single 4 bp oscillation cycle would have a probability p smaller than 0.025 (Fig. 3C, D). Across all lineages, we observed 8 novel 4 bp indel mutation events. Among them, six cases had 0 oscillations after the first 4 bp indel, while the remaining two cases had 1.5 and 2 oscillation periods after the first 4 bp indel. Under the null hypothesis that these oscillations were due to de novo mutations, the probability of observing 2 or more such events, which consist of at least 1 oscillation, among 8 cases has probability = 1 − [(1-p)⁸ + 8 p (1-p)⁷] = 0.016. Therefore, we conclude that the derived allele mechanism is unlikely to explain this result.

To assess the prevalence of the ancestral allele mechanism during adaptation, we note that across the experiment we observed 14 indels larger than 6 bp (using maximum parsimony), yet among these only a single case (lineage B4, 56 bp indels) had a TR oscillation. Moreover, we observed 2 TR oscillation among 8 indels of length 4 bp. Combining all indels > 2 bp, the ancestral allele mechanism is used with a frequency of (3/22)=0.14, indicating that selection on ancestral alleles in our experiment is a minority mechanism that accounts for ~ 14% of evolutionary trajectories of the populations. To confirm that this mechanism is not dominant in the experiment, we measured the survival frequency of different types of nodes. Under a null hypothesis that TR-oscillations are due exclusively to ancestral alleles, nodes within the TR-oscillation tracks should have a higher heterogeneity and thus higher survival frequency than nodes outside of these tracks. Instead, we find that survival frequencies for both nodes are comparable and close to 10⁻⁴, which is not significantly higher than the background mutation rate (Table S3).

Simulating TR length oscillations to infer frequencies of different adaptive mechanisms

To explicitly model the contribution of the ancestral allele mechanism to the evolutionary trajectories, we performed a detailed simulation of TR dynamics under fluctuating selection. In simulations, the cell division rate (fitness) of each cell was determined by the environment (selection/counter-selection) and by the URA3 reading frame. Cell divisions and indel mutations were simulated until the population reached a typical yeast colony size (about 2¹⁸ ~ 2²⁰ cells). We mimicked the colony passage step by partitioning the population into microcolonies having a Poisson-distributed bottleneck size n, and then switching the environment. Of the microcolonies that achieve a macroscopic size (>10⁴ cells) one is chosen randomly to initialize a new round (see Methods).

We recorded the population dynamics of allele frequencies as well as the individual mutational histories of all cells. The allele frequency dynamics, obtained by population census at regular intervals, indicates the bulk behavior of adaptive alleles after each environmental change. At the end of the simulation, a surviving cell is randomly chosen and its mutational history is traced backward in time through its ancestral lineage. Due to coalescence, which occurs on a timescale of the order of one environmental episode, the ancestral lineage is identical for all cells at all times before the last common ancestor of the population at the end of the simulation. It records the series of mutational events that fixed in the population, i.e. the derived allele mechanism.

In Fig 4, we simulated populations with average bottleneck size n = 5 or 50 cells, over 10 environmental changes. In both cases, we see that allele frequency dynamics track the environment: adaptive alleles perform a selective expansion in each environmental episode. Interestingly, this behavior can differ substantially from that observed in the ancestral lineage. For small bottleneck size (Fig. 4A), the ancestral lineage exhibits a novel mutation with each environmental switch, and the number of fixed indel mutations is equal to the number of environmental episodes. For larger bottleneck size (Fig. 4B), the ancestral lineage often persists through the non-adaptive phenotype with no mutations (e.g. the 4^th, 7^th, and 10^th environmental intervals), while the adaptive phenotype performs an incomplete sweep.

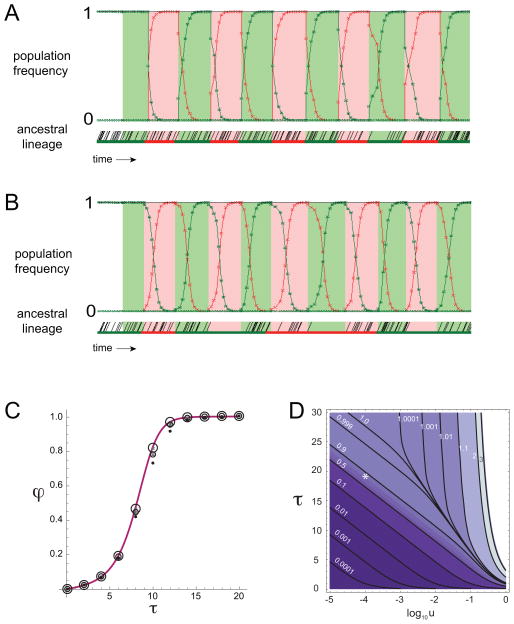
Figure 4. Modeling ancestral versus derived allelic diversity.

(A,B) Simulation of bulk population and ancestral lineage dynamics. Simulation results of population allele frequency and ancestral lineage, with population bottleneck size n = 5 in (A) and n = 50 in (B). Other simulation parameters are listed in Table S4. Red and green backgrounds represent selective and counter-selective environments, respectively. Upper panels: red and green curves represent the frequency of adaptive alleles for red and green environments. Bottom panels: red and green segments represent the allelic states adapted to red and green environments, respectively. Black diagonal segments represent cell divisions along the lineage.

(C,D) Analytical results for φ in the large population limit. (C) Comparison of theory (curve) and simulations (circles) for different population sizes as a function of τ. Simulations were run using a two-phenotype, two-environment model (Materials & Methods) using u = 0.01 for population sizes N_min = 50 (solid circles), 100 (medium circles), and 1,000 (large circles); N_max = 10 N_min in each case. Adapted and non-adapted phenotypes replicated with rates 1 and 0, respectively, which defines the time unit for the simulation. Error bars represent three standard deviations around the sample mean; error bars are not shown when smaller than the solid circle symbol size. (D) Analytically calculated phase diagram of φ as a function of τ and u, using the path integral approach described in the Appendix. Contours show the values of φ, while the asterisk denotes the parameter regime in the experiment. u and τ are both measured in appropriate units using the generation time of adapted individuals.

The bulk population dynamics look essentially indistinguishable for either ancestral or derived allele mechanisms, and alone cannot unambiguously classify the underlying adaption mechanism. However, this basic problem can be addressed by analyzing the ancestral lineage statistics. We define

$$\phi =\frac{\#\text{of}\text{mutations}\text{in}\text{the}\text{lineage}}{\#\text{of}\text{environmental}\text{episodes}\text{spanned}\text{by}\text{the}\text{lineage}}$$ (2)

This quantity is close to one when the derived allele mechanism dominates the dynamics, or close to zero when the ancestral allele mechanism is prevalent. While values of φ > 1 are possible, for small mutation rates lineages typically exhibit either one or no mutation per environment.

We estimated using indel data (see above) that the ancestral allele mechanism accounts for 14% of the adaptive events, i.e. in 86% of environments the lineage adapts using a recently derived allele yielding φ ~ 0.86. To determine whether this value is consistent with experiments, we ran simulations across a range of mutation rates and bottleneck sizes, and derived the approximate dependence of φ on these two parameters (Supporting Information & Fig. S5A). We showed that the prevalence of the derived allele mechanism increases with bottleneck size and decreases with the mutation rate. This is consistent with the fact that transferring more cells within the bottleneck facilitates selection on ancestral diversity, while increasing the mutation rate facilitates selection on novel diversity. We find that a bottleneck size of 1 – 10 cells, and a mutation rate within the experimentally measured range, yield values of φ comparable to the experimentally observed value.

Ancestral lineages of large populations under fluctuating selection

Our general formulation of the measure φ using the ancestral lineage is broadly applicable in many other contexts. For example, we can consider populations with multiple phenotypic or allelic states, multiple environments, and different environmental timescales. We present an exact numerical calculation of φ for any of these cases using a path integral formulation previously described in (Kussell et al. 2006; Leibler and Kussell 2010) and building on earlier work on ancestral distributions (Hermisson et al. 2002). The path integral approach considers a population as a collection of individual lineages that grow and evolve over time. For a large population over sufficiently long time, the statistical properties of its lineages approach a stationary distribution whose generating function can be derived. In the Appendix, we show how this approach is used to compute φ for a wide range of models. In certain special cases, φ can also be computed from bulk population dynamics, and gives consistent results with the path integral approach (see Supporting Information).

We used these exact results for large populations to analyze the dependence of φ on mutation rates and environmental timescales in a simple two-phenotype, two-environment model (Fig. 4). Rates and timescales were measured in time units corresponding to the generation time of the adapted phenotype. First, we considered a fixed mutation rate, and varied the environmental duration (Fig. 4C). We found close agreement between simulations (points) and analytical results (curve). For fast fluctuations, φ is extremely low indicating that population adaptation occurs mainly by maintaining ancestral alleles rather than by generating new mutations. For slow fluctuations, φ approaches the value one, indicating that the population has sufficient time in each environment to generate new mutations which are able to perform a selective sweep when the appropriate environment occurs. For intermediate timescales, the population employs a mixture of adaptive mechanisms. In this regime, the value of φ is sensitive to the total population size when Nu ≤ 1, as seen from the deviations of the smaller simulated populations (N = 50, 100) from both the exact solution (which neglects drift), and the larger simulated population (N = 1,000). These deviations are due to the smaller populations being in a mutation-limited regime; hence they employ the ancestral allele mechanism to a greater extent than a large population. Conversely, φ is insensitive to population size for very long or very short environmental durations. In the case of long durations, this results from the higher mutational supply per environment, while in the case of short durations it is due to environments fluctuating too fast for selection to be effective.

Comparing with experiments, we note that our propagation of the population involves dispersing an entire colony of size ~10⁵ onto a plate, and then picking a surviving colony. With respect to derived alleles, this procedure maintains a large effective population size, roughly similar to the original colony size, in which Nu ~ 10 – 100. With respect to ancestral alleles, we estimated that a population size of up to n = 400 ancestral cells are transferred with each colony passage, all of which have the adapted phenotype of the previous environment. Since Nu is comparable to n in the experiment, and both Nu and n are larger than 1, the results are not strongly affected by drift, and can be approximated in the large Nu regime of our model.

We summarized the dependence of φ in this model by analytically calculating the phase diagram, shown in Fig. 4D. For small mutation rate u, φ transitions from selection on ancestral alleles to derived alleles, e.g. from φ = 0.1 to 0.9, over a relatively narrow range of environmental durations. Below this transition region, the value of φ approaches zero exponentially with decreasing environmental duration τ. For very high values of either u or τ, it is possible for multiple fixation events to occur within a single environment. This happens when a mutation to the non-adaptive allele is not eliminated by selection and is subsequently reversed; such mutational trajectories, while rare, can contribute to the ancestral lineage for high mutation rates or long environmental durations.

Discussion

We studied an experimental yeast population that adapts to fluctuating selection by generating high levels of diversity at a tandem repeat locus. Due to the high rate of phenotypic switching at the repeat locus, evolved populations are able to track the environmental state over multiple episodes, with a low overall extinction rate. While populations that utilize stochastic switches are often assumed to adapt via newly generated alleles, we showed that selection on ancestral diversity can contribute significantly to their evolutionary dynamics.

We summarized the indel mutational spectrum based on either maximum parsimony or maximum novelty (Figs. 3A,B). Overall, 2 bp indels were most frequent, 4 bp indels the next most frequent, and large indels were the least frequent indel class. We found no significant insertion vs. deletion bias for 2 bp indels (Table S1, lineage A4, nodes 3 & 5). We found that large indels occur much more frequently in ON–>OFF selections (13 cases) than in OFF–>ON selections (1 case in lineage B2). When cells are passaged to the 5-FOA medium (ON–>OFF counter-selection), most of them are URA3⁺ hence they synthesize 5-FU. Among these cells, we expect that those in S-phase are particularly susceptible to 5-FU, which is known to be mutagenic (Seiple et al. 2006), and could therefore induce large indels during DNA repair.

Using a general theoretical framework, we showed that the population’s ancestral lineage, which records the precise order of adaptation by new mutations, can be calculated exactly and provides a natural measure φ that quantifies the evolutionary dynamics. Analyzing our experimental results, we found that φ lies in the range of 80–90%, indicating that the population adapts to fluctuating selection by a mixture of adaptive mechanisms, in which the derived allele mechanism is more frequent. We further used a mathematical model and simulations to study the dependence of φ on experimental parameters. Intuitively, increasing the mutation rate u increases the rate at which novel mutants are generated, hence φ will increase; while increasing the bottleneck size n during passage increases the available ancestral diversity, hence φ will decrease.

The relationship between bulk population dynamics and the dynamics we observe along the ancestral lineage is complex. When environmental changes are rare, one can effectively describe the population’s behavior using hard and soft sweeps, and capture the essential features of the dynamics (Hermisson and Pennings 2005; Pennings and Hermisson 2006; Karasov et al. 2010). These analytical approaches are more difficult to apply in a continually changing environment, when selective expansions can be interrupted by environmental changes. For example, under fluctuating selection the population dynamics over short timescales (spanning a single environment) may be dominated by incomplete sweeps, while over longer timescales (spanning multiple environments) the population efficiently fixes novel beneficial mutations with each environmental episode. A qualitatively similar situation exists for an adapting population climbing a fitness gradient (Desai et al. 2013) – such populations fix mutations while generating new mutants without ever completely quenching their diversity. Our exact calculation of ancestral lineage statistics provides a possible resolution of this problem in fluctuating environments.

We used a general path integral approach to compute φ in the large population limit (Appendix). Using simulations, we demonstrated that the large population limit correctly describes the behavior of finite populations provided that Nu > 1 (Fig. 4C). We showed that the transition between ancestral and derived allele mechanisms, e.g. spanning the range φ = 0.1 to 0.9, occurs over a relatively narrow range of the environmental duration τ (Fig. 4D). In the experiment, we found that φ is within this transition region, and we predict its value would decrease dramatically for slightly smaller values of τ. Our theoretical results point to the sensitivity of evolutionary dynamics to environmental timescales, and to the importance of precisely controlling these variables in evolution experiments. Analytical quantification of adaptation dynamics using φ is flexibly applicable in many other contexts and models, including multiple phenotypes, genotypes, environments, and timescales. Further generalizations could include the effects of extinction as well as fluctuations around the dominant ancestral lineage using more detailed stochastic models. Direct experimental measurement of φ requires the use of lineage tracking techniques, which are currently available in single-cell experiments (Lambert and Kussell 2015), and may become possible in bulk experiments using variations of barcoding methods (Levy et al. 2015).

Appendix A: Lineage Formulation of Evolutionary Dynamics

We consider a population consisting of a finite number of genotypic (or phenotypic) states, that reproduce and mutate (or switch) with rates that depend on both the phenotypic and the environmental state, 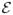. Indexing the genotypic states by i, the mutation rate from type j to type i is denoted by $u_{ij}^{\mathcal{E}}$, and the fitness is denoted $f_i^{\mathcal{E}}$. We define $u_{ii}^{\mathcal{E}}\equiv {\sum }_{k\ne i}{u}_{ki}^{\mathcal{E}}$ to be the total rate of mutation of genotype i. The environmental state at time t′ will be denoted 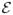(t′); and we consider the time series of environments to be fixed.

In (Leibler and Kussell, 2010), the distribution of individual histories in the large population limit was derived, which we briefly summarize. At time t, which we assume is very long compared to all given rate constants, the population consists of N(t) individuals, each of which is associated a specific genotypic history, σ(t′), defined for 0 ≤ t′ < t. This history specifies the genotype of all cells along the ancestral lineage that led up to the present cell (we assume asexual reproduction, hence a single parent at each cell division). Each history is characterized by its a priori probability, P_σ, which gives the probability of observing σ in the absence of fitness differences; and by its historical fitness,

$$F_{\sigma }={\int }_0^t{f}_{\sigma (t^{\prime })}^{\mathcal{E}(t^{\prime })}d{t}^{\prime }.$$ (A1)

Note that P_σ depends only on the mutation rates $u_{ij}^{\mathcal{E}}$, while F_σ depends only on the fitness values $f_i^{\mathcal{E}}$. The total number of cells in the population having history σ can be written as X_σ = P_σe^F_σ, and summing this over all histories (a path integral) gives the total expected population size,

$$N(t)=\int X_{\sigma }\mathcal{D}\sigma .$$ (A2)

From this expression, one obtains the long-term growth rate of the population in the long time limit, Λ ≃ (1/t) log N(t). As detailed in (Kussell et al., 2006; Wakamoto et al., 2012), the path integral at long times is dominated by a small set of histories – which we call optimal lineages – that maximize a tradeoff between fitness and entropy (i.e. the logarithm of P_σ). These optimal lineages are the most likely history of a randomly chosen cell, and as t gets large, they become exponentially more likely than any other history. In a finite size population, due to coalescence, all individuals at time t share a single ancestral lineage for t′ < t_coalesce. Different realizations of the stochastic processes of mutation and selection in each population will select a unique optimal lineage. However, these optimal lineages all share the same statistical properties, which are directly computable from the path integral, as shown below.

The ancestral lineage records the series of mutational events that were fixed in the population. We can explicitly compute the frequency of different quantities along the ancestral lineage by appropriate derivative of Λ. For example, we denote by ρ_σ(i, 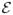) the joint frequency of genotype i and environment 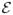along a history σ, and we would like to compute its value ρ_*(i, 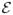) for optimal lineages. First, we note that from (A1) we have

$$\frac{\partial F_{\sigma }}{\partial f_i^{\mathcal{E}}}=t{\rho }_{\sigma }(i,\mathcal{E}),$$ (A3)

from which it follows that

$$\frac{\partial \mathrm{\Lambda }}{\partial f_i^{\mathcal{E}}}=\underset{t\to \infty }{lim}\frac{\int {\rho }_{\sigma }(i,\mathcal{E})X_{\sigma }\mathcal{D}\sigma }{N(t)}\to {\rho }_{\ast }(i,\mathcal{E})$$ (A4)

since the path integral is overwhelmingly dominated by optimal lineages. Hence, derivatives of the long-term growth rate can be used to compute the mean frequency of genotypes along the ancestral lineage.

Similarly, we can compute the joint frequency of j-to-i mutations in environment 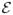along a history σ, which we denote by ρ_σ(j → i, 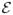). To see this, we explicitly express the a priori probability of the history as

$$P_{\sigma }=exp\left[-t\sum _{i,\mathcal{E}}{u}_{ii}^{\mathcal{E}}{\rho }_{\sigma }(i,\mathcal{E})\right]\prod _{i\ne j,\mathcal{E}}{(u_{ij}^{\mathcal{E}})}^{t{\rho }_{\sigma }(j\to i,\mathcal{E})}$$ (A5)

$$=exp\left[-t\sum _{i,\mathcal{E}}{u}_{ii}^{\mathcal{E}}{\rho }_{\sigma }(i,\mathcal{E})+t\sum _{i\ne j,\mathcal{E}}{\rho }_{\sigma }(j\to i,\mathcal{E})log{u}_{ij}^{\mathcal{E}}\right].$$ (A6)

The exponential term in (A5) accounts for the probability of not mutating along the entire history (except at a countable number of points); while the product term accounts for the probability of the actual mutations that occur. We then obtain the relation

$$\frac{\partial P_{\sigma }}{\partial log{u}_{ij}^{\mathcal{E}}}=t{\rho }_{\sigma }(j\to i,\mathcal{E})P_{\sigma }$$ (A7)

using which we calculate

$$\frac{\partial \mathrm{\Lambda }}{\partial log{u}_{ij}^{\mathcal{E}}}=\underset{t\to \infty }{lim}\frac{\int {\rho }_{\sigma }(j\to i,\mathcal{E})X_{\sigma }\mathcal{D}\sigma }{N(t)}\to {\rho }_{\ast }(j\to i,\mathcal{E}).$$ (A8)

The rate of mutations along the ancestral history can thus be computed by differentiating Λ with the respect to the logarithm of the appropriate mutation rate, but without changing the total mutation rates, $u_{ii}^{\mathcal{E}}$, which can be absorbed into the fitness coefficients $f_i^{\mathcal{E}}$.

The quantity φ defined in the main text can be computed as the total frequency of all mutations over the ancestral lineage times the mean environmental duration, τ̄, or

$$\phi \equiv \overline{\tau }\sum _{i\ne j,\mathcal{E}}{\rho }_{\ast }(j\to i,\mathcal{E}).$$ (A9)

To explicitly compute φ in the simple model used in the text, be specialize to the case of two phenotypes and two environments. We assume a single mutation rate u, which does not depend on the environment, and let f_a and f_na denote the growth of adapted and non-adapted phenotypes in each environment. Both environments last an equal duration, τ. We define two matrices,

$$A=\left(\begin{array}{cc}{f}_a-u& \gamma u\\ \gamma u& f_{na}-u\end{array}\right)B=\left(\begin{array}{cc}{f}_{na}-u& \gamma u\\ \gamma u& f_a-u\end{array}\right)$$ (A10)

using which the long-term growth rate can be computed as

$$\mathrm{\Lambda }=\frac{1}{2\tau }log{\lambda }_1(e^{\tau A}{e}^{\tau B})$$ (A11)

where λ₁(·) denotes the maximal eigenvalue of the given matrix. This yields

$$\phi ={\tau \frac{\partial \mathrm{\Lambda }}{\partial \gamma }|}_{\gamma =1}.$$ (A12)

which can be computed numerically, or approximated analytically for small or large τ using the methods described in (Leibler and Kussell, 2010). Models with larger numbers of phenotypes in a periodically changing environment are amenable to exactly the same calculation. For a randomly fluctuating environment, one must first compute Λ conditioned on the temporal realization of the environment, 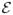(t), then average over realizations according to the random environmental process.