Abstract.
The evaluation of medical imaging devices often involves studies that measure the ability of observers to perform a signal detection task on images obtained from those devices. Data from such studies are frequently regressed ordinally using two-sample receiver operating characteristic (ROC) models. We applied some of these models to a number of randomly chosen data sets from medical imaging and evaluated how well they fit using the Akaike and Bayesian information criteria and cross-validation. We find that for many observer data sets, a single-parameter model is sufficient and that only some studies exhibit evidence for the use of models with more than a single parameter. In particular, the single-parameter power-law model frequently well describes observer data. The power-law model has an asymmetric ROC curve and a constant mean-to-sigma ratio seen in studies analyzed with the bi-normal model. It is identical or very similar to special cases of other two-parameter models.
Keywords: receiver operating characteristic models, Akaike information criterion, cross-validation
1. Introduction
To evaluate the effectiveness of an imaging technology, researchers may perform a controlled diagnostic observer study where human or model observers use images to differentiate diseased patients from nondiseased patients or, more generally, images with a signal from images with no signal.1 Because collecting cases and performing such studies can be expensive, the numbers of cases and readers in these studies are usually small or just large enough to detect a modest change in a particular statistical performance metric. The value of this metric and its estimated uncertainty are often derived using ordinal regression to a semiparametric model of the data.2 The area under the receiver operating characteristic (ROC) curve (AUC) is often used as such a performance metric because it is reproducible and likely to predict real clinical performance.
In these studies, each observer gives a rating of his confidence that there is a signal in an image. For example, a radiologist may give a rating of his confidence that a lesion exists in a mammogram. The ROC curve characterizes the relationship between the distribution of the observer’s ratings of signal-present images and the distribution of ratings of the signal-absent images.3
There are many semiparametric ordinal regression models that have been used for modeling observer data and ROC curves,2,4–8 particularly in medical imaging experiments. Typically, we utilize these semiparametric models on ordered categorical observer ratings that we collect from human observer experiments. The data may be categorical by study design, e.g., ratings that run one through five, or the data may be categorical because the observers gave many images the same rating, e.g., 0 or 100. For these experiments, semiparameteric models can give significantly different results from nonparametric ROC analyses9 and, therefore, we may be interested in the results of both. In these models, observer ratings themselves are not assumed to be distributed like these models but can be monotonically transformed to a latent model space with an equal ROC curve. Some models are chosen because they have desirable properties. For example, semiparametric models with monotonic likelihood ratios generate concave ROC curves, imply that the observer is rational, and will not systematically rate images with a signal or disease lower than those without.
Typically, statisticians use criteria such as the Akaike and Bayesian information criteria (AIC and BIC) to determine appropriate models or a number of model parameters for a data set of interest.10 In general, the number of model parameters is selected using the principal of parsimony, where simpler models are preferred and additional parameters are used only if we can demonstrate that they are needed. We can pose the problem as a hypothesis test, where the simpler model is the null hypothesis and we reject it for the alternative hypothesis (complex model) only if the probability of the null hypothesis is significantly smaller than the alternative. In the scenario where one model is a special case of a complex model with more parameters, we can estimate these probabilities using the approximation for the likelihood ratio test (LRT). The authors know of no publications that compare different semiparametric ROC models or numbers of model parameters on observer data using these standard techniques.
This paper applies some semiparametric models to a number of studies from medical imaging. We examine AIC, BIC, and the results of cross-validation. We find that for many observer data sets, a single-parameter model is sufficient to describe the data. In particular, the single-parameter power-law model frequently well describes observer data.
Other authors have noted that the power-law ROC model fits several data sets well and that a particular form of the power-law model suggests a kind of decision making that uses extreme values.11,12 Interestingly, these models suggest that observers distribute their ratings such that the lowest ratings are the most extreme.
2. Models
The ROC curve is the two-dimensional plot of the survival function of the signal-present observations versus the survival function of the signal-absent observations, or the plot of all true positive fractions (TPF) versus false positive fractions (FPF). Examples of ROC curves are shown in Fig. 1. Here, we let and represent signal-absent and signal-present cumulative distributions. Likewise, and represent those cumulative distributions in a transformed space, and and represent the respective densities. In what follows, we will use variables , , and to represent the values latent ratings under various models.
Fig. 1.
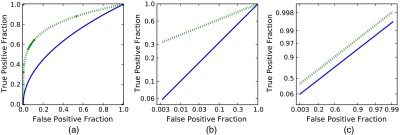
Each of the graphs shows the same two power-law receiver operating characteristic (ROC) curves plotted on three different scales. The solid ROC curve has , and the dotted ROC curve has . The scale in (a) is uniform in probability and demonstrates the characteristic asymmetric or skewed power curve . FPF, false positive fractions; TPF, true positive fractions. Graph (b) has a logarithmic probability scale, and here is the inverse of the slope of the ROC curves. Graph (c) has a double negative logarithmic scale and is the offset of the ROC curves.
In this paper, we examine several two-sample models for and : (1) the unequal variance bi-normal model,2 (2) the equal variance bi-normal model, (3) the bi-gamma model,4,5 and (4) the power-law model.4,13,14
The paper examines how well these models fit ROC data collected from observer experiments. Note that these are models for the ROC curves, not the observer ratings, which may differ via a monotonic transformation. While many other ROC models exist, the above were chosen because they are common and because the one-parameter models are special cases of the two-parameter models. All the above models, except the unequal variance bi-normal model, have monotonic likelihood ratio functions and generate concave ROC curves. In general, ROC models with more parameters will attain greater likelihoods, i.e., Eq. (3) of Dorfman and Alf2 will have higher values for models with more parameters. Models with fewer parameters will be simpler to implement and may offer more statistical power. Models with only one parameter, such as the power-law model and the equal variance bi-normal model, offer a one-to-one correspondence between the model parameter and the AUC.
2.1. Bi-Normal Model
The unequal variance bi-normal model assumes that the distributions of reader ratings can be monotonically transformed to two normal distributions, one for signal-absent images and one for signal-present images. This model can be described by two parameters: the difference of means and the ratio of the standard deviations of the two normal distributions , e.g.,
| (1) |
Unlike other models presented in this work, the bi-normal model does not, in general, have a likelihood ratio that is monotonically increasing everywhere. This model is not proper, in the sense that it does not yield a concave ROC curve. In this paper, this model is abbreviated as .
2.2. Equal Variance Bi-Normal Model
This model is a special case of the bi-normal model where the two normal distributions are required to have equal standard deviations, i.e., . This simpler model results in a concave ROC curve and, thus, has a monotonic likelihood ratio. This model is the only model used in this work that is constrained to be symmetric. All other models assume that one distribution may have larger variance than the other. In this paper, this bi-normal model is abbreviated as .
2.3. Bi-Gamma Model
The bi-gamma model assumes that the distributions of reader ratings can be monotonically transformed to two gamma distributions:
| (2) |
| (3) |
where is the shape parameter and is the scale parameter. In this model, , , and . When , the model becomes a single-parameter exponential or power-law model as described in the next section. In this paper, the bi-gamma model is abbreviated as .
2.4. Power-Law Model
The power-law4 or exponential3 model assumes a power-law relationship between the FPF and the TPF, i.e.,
where is the single parameter that measures the degree of separation between the signal-present and signai-absent distributions. When the signal-present and signal-absent distributions are indistinguishable, , and when the signal-present ratings are higher, on average, than the signal-absent ratings. Hanley and McNeil15 used the power-law model to calculate the uncertainty on the AUC.
The power-law ROC curve can arise from the power-law4 or Pareto models for latent ratings distributed in the form , where and . For mathematical convenience, we set for a signal-absent distribution and for the signal-present distribution
| (4) |
| (5) |
Note that
Because the ROC curve is invariant under monotonic transformations of the rating data, a number of pairs of common distributions that yield the same ROC curves can be constructed from these power-law forms. In general, if is the transformed variable and is a monotonic function, then is the distribution of the transformed variable. Distributions that give ROC curves equal to the power-law distributions include the following:
-
1.
The transformation yields Weibull distributions from the power-law distributions, , , where . For , the distributions are negative exponentials and are a specific case of the bi-gamma model where . For , the distribution is Rayleigh, which arises from random sinusoidal noise.3,4
- 2.
-
3.The transformation yields likelihood ratio distributions.
(8)
where the likelihood ratio is .(9)
Examples of power-law ROC curves arising from these distributions are shown in Fig. 1 on three different scales.
3. Model Fitting
This paper examines how well the above four models represented data from a number of studies listed in Sec. 4. We fit each data set with each of the four models using two-sample maximum likelihood (ML) ordinal regression,2,17–19 which is a typical approach in observer performance studies. The selected model parameters were those that gave the greatest model likelihood. We used three approaches to evaluate the goodness-of-fit of these ML models: (1) the AIC20 and BIC,21 (2) the LRT, and (3) cross-validation.
3.1. Akaike and Bayesian Information Criteria
AIC is expressed as , where is the number of free parameters in the model and is the maximum likelihood of the fit model. It defines a trade-off between the number of parameters used to fit the data and the likelihood of the fit. Less parsimonious models are penalized for having more parameters. Lower values of the criterion indicate better models.
Likewise, BIC is defined as , where is the number of independent observations to which the model is fit. BIC penalizes extra model parameters more strongly than does AIC.
The true number of free parameters for each model is difficult to estimate because it depends upon the number and distribution of the latent threshold parameters in the ordinal regression procedure. These latent thresholds are parameters that correspond to the boundaries between actual numerical ratings. These parameters are dependent upon each other because they are constrained to be ordered and, therefore, they should not be considered full free parameters. Therefore, exact values of AIC and BIC cannot be calculated. However, because we ensured that the number of latent thresholds is the same for all models for any one particular data set, we made the assumption that the latent thresholds for all models contribute the same effective number of free parameters. In that case, we do know the differences in the number of free parameters between models, and therefore, the differences in AIC and BIC can be estimated.
In the situation where two models being compared have the same number of parameters, such as the power-law and equal variance bi-normal model or the bi-gamma model and the bi-normal model, the difference in AIC and BIC is just twice the log-likelihood ratio, e.g., . In this case, selecting the model with the lower AIC or BIC is equivalent to selecting the model with the highest likelihood. A difference in AIC or BIC of corresponds to one model being times more likely than the other.
The bi-gamma () and bi-normal () models have one more degree of freedom than the power-law () or equal variance bi-normal () models. In the situation where the two models being compared differ by one parameter, such as the and models, the difference in AIC is .
AIC and BIC were developed as general rules for determining which model should be selected given a particular data set. These rules can be applied to any pair of models, even if no known statistical test exists for the likelihoods of the models. For more details about these criteria, the reader is encouraged to consult the references.
3.2. Likelihood Ratio Test
Wilks22 demonstrated that if the data are distributed like that of a simpler model , and if is a special case of another model that has more parameters, then the ML log-likelihood ratio is approximately distributed as a variable with degrees of freedom. Therefore, if an observer’s data are truly distributed in a power-law fashion, then will be approximately distributed as . If we were to select the model with the lower AIC, then there is a probability that we would violate parsimony and select the model with one more degree of freedom than necessary. Likewise, if an observer’s data set of 140 observations is truly distributed as the equal variance bi-normal model, then the difference in BIC between a two-parameter ML bi-normal model and a one-parameter ML bi-normal model will be distributed approximately as . If we were to select the model with the lower BIC, then there is a probability that we would not select the true parsimonious model.
Frequently, statisticians treat the extra model parameter as an alternative hypothesis and the LLR as a test statistic. If the LLR is greater than of the appropriate distribution, then we may reject the simpler model and accept the extra model parameter. In this LRT, the LLR threshold is the one-sided 95% confidence interval (CI).
The empirical differences of the log-likelihood, AIC, and BIC were calculated for each observer and modality for every study described in Sec. 4. The differences were also calculated for each of the 4010 data sets in each simulation. The distributions of these differences are given in Fig. 2, and the fraction of individual ROC curve fits preferred by each criterion are given in Table 1.
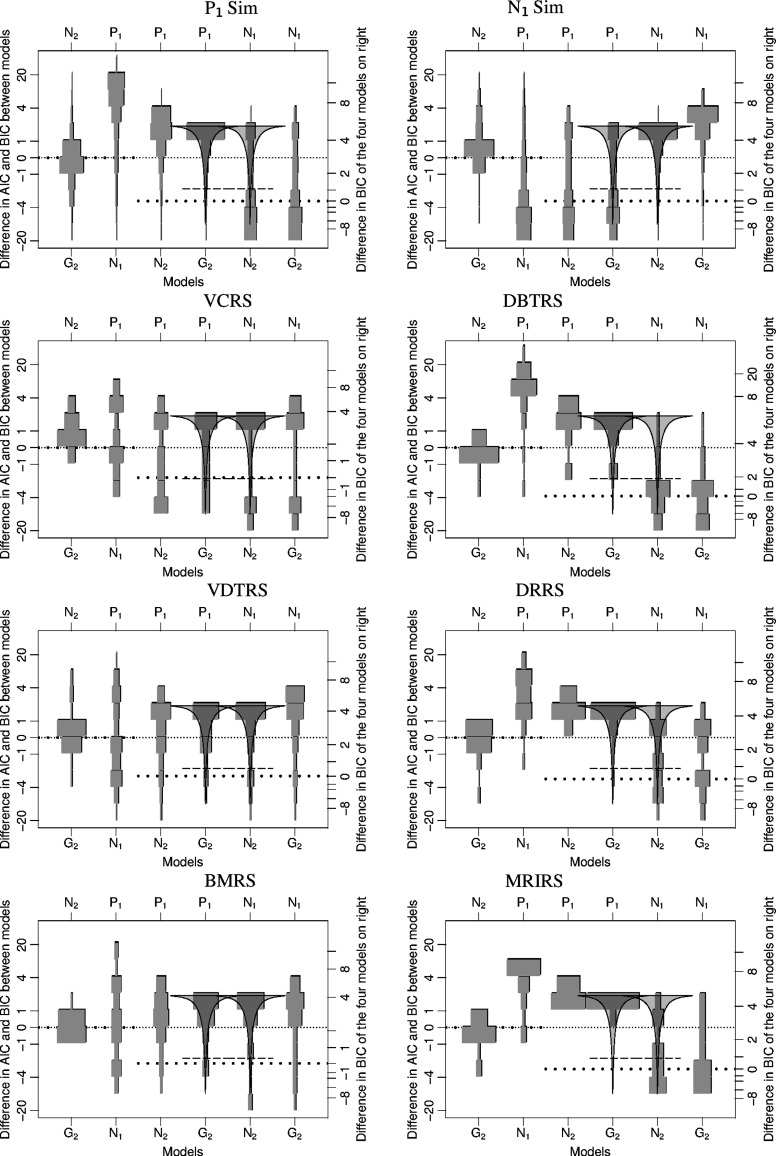
Fig. 2.
This figure contains eight plots, one for each study. The top two plots are from the power-law () and normal () simulations, and the lower six plots are from real studies. Each plot shows the empirical distributions of the differences of Akaike information criterion (AIC) and Bayesian information criterion (BIC) between each pairing of the four models. There is one such difference for each reader and for each modality. All distributions are normalized to have the same area, though the real studies have sample sizes between 8 and 100, and the simulated sample sizes are 4010. At the top and bottom of each plot are the identifiers of the models being compared. For example, on the far left of each plot is the distribution of the difference of AIC and BIC values between the two-parameter bi-gamma () model and the two-parameter bi-normal () model. Because lower AIC/BIC values indicate superior fits, a distribution mostly above zero would indicate superiority of the model. The scale on the left is the difference in AIC that applies to all six distributions in each plot. The BIC difference scale for the two left-most distributions is the same as the AIC difference scale because the models being compared have the same number of parameters. The BIC difference scale on the right applies to the four distributions on the right of each plot. The densely dotted, narrow, horizontal lines in the plots are at a value of 0 difference in AIC. The sparsely dotted, thick, horizontal lines are at a value of 0 difference in BIC. The solid curved lines are the probability density of . This curve is the approximate expected distribution of the difference of two AIC values if the upper model represents the actual population and the lower model has an additional parameter.22 The dashed horizontal line is the 5% lower confidence interval on that expected distribution.
Table 1.
This table gives the percentage of fits that favor the first of the two listed models based on a particular criterion for each study. For example, the number in the upper left indicates that Akaike information criterion (AIC) and Bayesian information criterion (BIC) favored the bi-gamma model over the bi-normal model for 60.5% of the power-law simulations. These numbers are the percentages of each distribution in Fig. 2 below the finely dotted lines (AIC), coarsely dotted lines (BIC), and dashed lines [95% confidence interval (CI)]. In Sec. 3.2, we approximated the values in the asterisk cells as 15.7, 2.6, and 5.0%.
| Models | Criteria | Sim | Sim | VCRS | DBTRS | VDTRS | DRRS | BMRS | MRIRS |
|---|---|---|---|---|---|---|---|---|---|
| A/BIC | 60.5 | 22.2 | 12.5 | 75.0 | 34.7 | 53.6 | 50.0 | 70.0 | |
| A/BIC | 13.3 | 83.2 | 50.0 | 7.1 | 59.4 | 3.6 | 46.7 | 10.0 | |
| AIC | 15.4 | 71.9 | 62.5 | 10.7 | 38.6 | 0.0 | 33.3 | 0.0 | |
| BIC | 2.8 | 45.8 | 50.0 | 0.0 | 11.9 | 0.0 | 6.7 | 0.0 | |
| AIC | 18.5* | 71.6 | 50.0 | 14.3 | 35.6 | 7.1 | 26.7 | 0.0 | |
| BIC | 3.5* | 42.6 | 25.0 | 0.0 | 7.9 | 3.6 | 6.7 | 0.0 | |
| CI | 6.0* | 52.2 | 25.0 | 0.0 | 9.9 | 3.6 | 10.0 | 0.0 | |
| AIC | 76.1 | 16.8* | 37.5 | 92.9 | 32.7 | 64.3 | 30.0 | 70.0 | |
| BIC | 50.6 | 2.9* | 37.5 | 42.9 | 15.8 | 21.4 | 13.3 | 30.0 | |
| CI | 59.1 | 5.4* | 37.5 | 82.1 | 17.8 | 35.7 | 13.3 | 60.0 | |
| AIC | 78.2 | 10.2 | 37.5 | 92.9 | 26.7 | 64.3 | 30.0 | 80 | |
| BIC | 53.2 | 2.1 | 37.5 | 46.4 | 11.9 | 25.0 | 13.3 | 40 | |
| Number of fits | 4010 | 4010 | 8 | 28 | 101 | 28 | 30 | 10 | |
Additionally, for the pairs of models where the LRT could be applied ( and ), we also calculated an overall probability ( value) of the null hypothesis that all the data in each study were from the more parsimonious one-parameter model. This value is the cumulative probability of the sum of the LLRs from all ROC curve fits from that study. Here, is the adjusted number of degrees of freedom, which is the number of LLRs multiplied by a correction factor. That correction factor is the ratio of the observed sum of LLR values from simulations to the theoretical value. The correction factors are very close to one, but are implemented because the LRT is not exact, only approximate.
Even with this correction, we still expect that our overall values that are less than will be underestimated because we do not account for correlations among the ROC curve fits within each study. By merely summing the LLR values, we assume independence, but because multiple fits from the same study may involve the same set of readers or patients,23 the LLRs may be correlated. Currently, we know of no implementations of a two-way random effect analysis for ML LLRs from a two-sample regression.
3.3. Monte Carlo Cross-Validation
Each set of observer data was randomly divided into two portions: one that contained 2/3 of the observations and another that contained 1/3. The larger portion of data was used to create a ML fit for each of the four models. We calculated the likelihood that the held-out data (the 1/3) came from each model with those ML fit parameters. This procedure was repeated several hundred times per observer per study. The signal-absent and signal-present distributions were sampled independently, so their relative proportions remained the same.
Models with too few parameters will not be able to represent the data well and the likelihood on the held-out data will be poor. Models with too many parameters will overfit the 2/3 training data set, excessively deviating from the true distribution of ratings, and will not generally perform as well as the true model on the held-out data. The average likelihoods from these Monte Carlo cross-validations were compared across models for each study and are shown in Fig. 3.
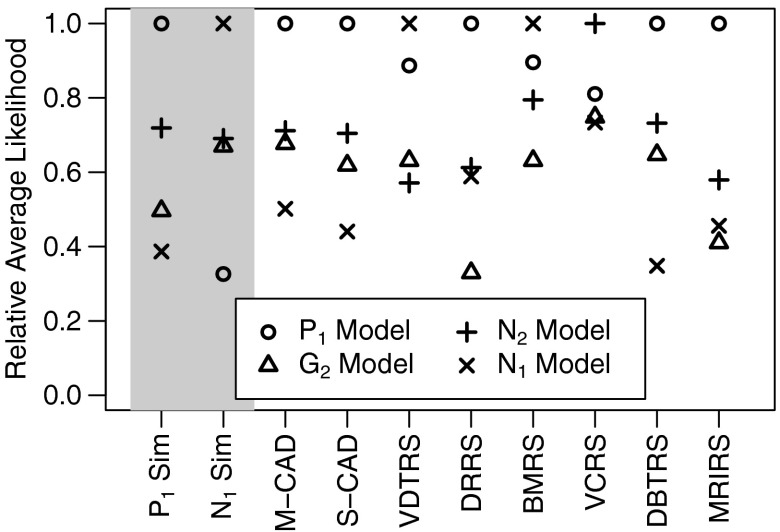
Fig. 3.
This figure plots the relative average likelihood of each of the four models on the 1/3 of the data held-out during cross-validation for each study in this paper. The average likelihoods of all models are divided by the likelihood of the model with the highest likelihood for that study, i.e., the likelihoods are normalized, so the model with the highest likelihood is scaled to 1. The shaded studies on the left are the simulated data sets provided for reference.
4. Studies and Data Sets
The models described in Sec. 2 were compared using AIC, BIC, LRT, and cross-validation (Sec. 3) on data from eight different observer studies and two computer simulations. The authors selected these studies randomly from those available or readily obtainable from collaborators without consideration of the distribution of data. The studies are typical of those found in medical imaging and are appropriate for comparing semiparametric ROC curve fits.
The data from each study consisted of ordered ratings given to a set of images. Some rating scales had 5 categories, some had 100, and some were between those values. Each rating represented the confidence with which the observer thought a signal was present in the image. All data were collected from rating procedures, not from forced choice or yes-no experiments. Because observers may differ on their rating scales and ability, each ROC model was fit separately to each observer’s ratings for each data set, therefore, each observer’s set of ratings had to include at least 10 signal-present and signal-absent images. No data sets were excluded based on the form of data distributions, so comparisons of models on these selected data sets should not be biased.
We excluded data from observers whose empirical AUC estimates were greater than and those less than . In general, data sets with high empirical AUC values, e.g., , have very few overlapping observations and, therefore, give little information about the form of the signal-present distribution with respect to the signal-absent distribution. Likewise, when AUC values are very low, , there is little information about the forms of the latent signal-present and signal-absent distributions, other than that they are not differentiated.
In most of the studies, the same set of images were evaluated by all observers in the study. Therefore, multiple ROC curves obtained from each study are not independent. All study data sets were completely de-identified both in readers and patients. For more details about a particular study, the reader may consult its respective reference.
4.1. Simulations
For reference and validation of our analysis methods, we compared models fitted to simulated data of two known types. One type of simulation used ratings drawn from power-law () distributions and the other from an equal variance bi-normal model (). We generated 4000 random data sets for each of these types of simulations to acquire the distributions of the differences of AIC and BIC for each pair of models in Sec. 2. Each single data set was composed of 70 signal-present ratings and 70 signal-absent ratings. These sample sizes were chosen to be typical of the real data sets analyzed in this paper. The AUC value for each data set was randomly chosen between 0.6 and 0.95.
4.2. Virtual Colonoscopy Reader Study
Petrick et al.24 describe a virtual colonoscopy study that consisted of four radiologists identifying and rating polyps in virtual colonoscopy images from 44 patients. The radiologists made two evaluations: one without the use of computer-aided diagnostic (CAD) software and one with the software. Eight total ROC data sets were fit, one for each reader and reading mode. This study will be abbreviated as VCRS.
4.3. Digital Breast Tomosynthesis Reader Study
In a study by Rafferty et al.,25 14 radiologists gave ratings on breast images from 312 patients, 48 of whom had confirmed malignant breast cancer lesions. Each radiologist gave two ratings for each patient, one using only mammography and one using mammography and tomography, leading to 28 different ROC data sets. This study will be abbreviated as DBTRS.
4.4. Volumetric Detection Tasks Reader Study
In a study described by Platiša et al.,26 10 to 12 observers gave ratings to simulated multislice and single-slice images generated with several different noise backgrounds. After the exclusions for extreme AUC values, a total of 101 ROC data sets were fit to the four models. Between 64 and 94 image ratings were used to construct each curve. This study will be abbreviated as VDTRS.
4.5. Digital Resolution Reader Study
In a study by Chan et al.,27 seven radiologists examined images of 112 microcalcification clusters that were digitized from mammograms at four different resolutions. Sixty-five of the clusters were benign. The radiologists rated how likely it was that each calcification cluster was malignant based on the image. This resulted in 28 ROC data sets. This study will be abbreviated DRRS.
4.6. Breast Mass Reader Study
In a study by Sahiner et al.,28 10 radiologists rated breast images from 67 patients that contained breast masses, 35 of which were malignant. The radiologists first read mammograms, then added three-dimensional ultrasound volumes, and then read both images with the assistance of a CAD device. All reader-modality permutations yield 30 different ROC data sets. This study will be abbreviated BMRS.
4.7. Magnetic Resonance Image Reader Study
In a study by VanDyke et al.,29 five radiologists interpreted single spin-echo magnetic resonance images (SE MRI) and cinema-mode magnetic resonance imaging (CINE MRI) images of 114 patients, 45 of whom had an aortic dissection. This gave 10 different data sets to be fit with ROC curves. This study will be abbreviated MRIRS.
4.8. Artificial Observers—CAD Data Sets
In addition to the studies with human readers, we include data from two artificial observers. One is the CAD software designed to mark masses on ultrasound and x-ray mammography images used in the reader study by Sahiner et al.28 The study is the same as described in Sec. 4.6. This study will be abbreviated M-CAD.
The other artificial observer is a software CAD designed to identify sclerotic metastases in computed tomography (CT) images of the spine.30 The CAD software was applied to images from 38 patients with bone lesions. For our analysis, each patient image was divided into six regions, with 130 of those regions containing metastases and 98 containing none. This study will be abbreviated S-CAD.
Each artificial observer output continuous ratings, but these scores were finely discretized18 to facilitate the ordinal regression routines used for reader data. Each artificial CAD observer yielded only single point estimates, rather than distributions, of differences in AIC and BIC. The ROC data and model fits of these are shown in Fig. 4.
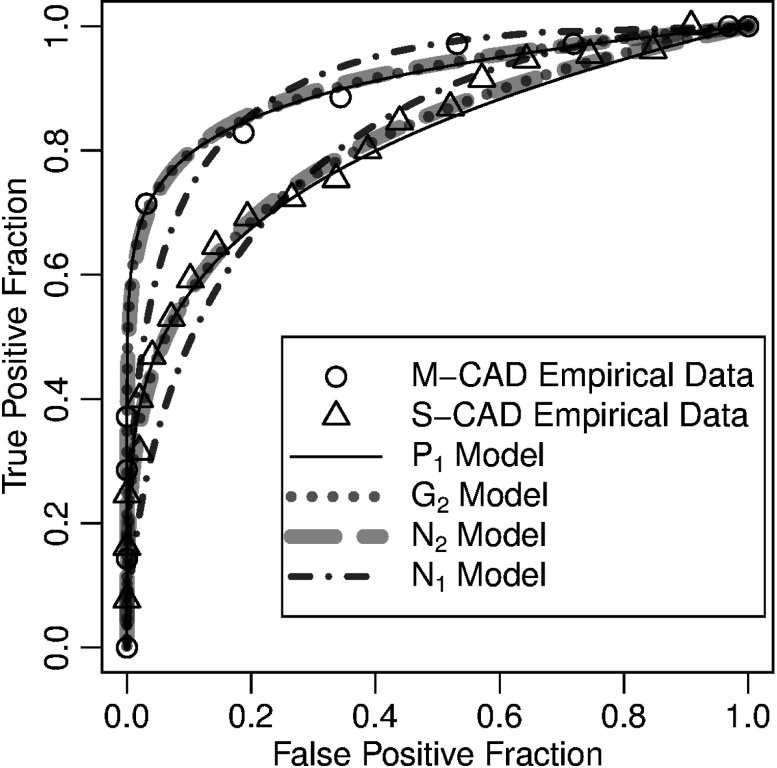
Fig. 4.
: ROC curves of the two computer-aided diagnostic (CAD) observers described in Sec. 4.8. The upper curves are from the mammography CAD. The lower curves are from the spinal CAD. The open circles and triangles are the categorized empirical ROC data. All other curves are semiparametric fits to those empirical data as described in the legend. Note that the power-law model and the two-parameter models are very similar for both CADs, and both data sets depart substantially from the single-parameter normal model.
5. Results
5.1. Differences in AIC and BIC and the LRT
The distributions of all the differences in AIC and BIC for each of the studies are shown in Fig. 2. For each study, the distributions of differences of each possible pairing of models are presented along the vertical axes.
The fractions of the distributions above the finely dotted, horizontal zero line are the fractions of differences in the AIC that favor the models listed across the top of the plot over the models listed on the bottom. The fractions of AIC differences below this line, and, therefore, showing preference for the model listed across the bottom, are given in Table 1 on the rows labeled AIC.
The fractions of the distributions above the coarsely dotted, horizontal zero lines are the fractions of differences in BIC that favor the model listed across the top. Note that this coarsely dotted line is in a different position for the two model comparisons on the left of each plot than the four on the right, because the four histograms on the right compare models that differ by one parameter. Fractions of BIC differences below this line are given in Table 1 on rows labeled BIC.
For the model pairings where one model is a special case of a more complex model, a dashed horizontal line indicates the approximate 95% one-sided lower CI for LRT. The percentages of fits below these thresholds are tabulated in Table 1 on rows labeled CI.
5.1.1. Simulations
The differences of AIC and BIC for the simulated data sets (the top two plots in Fig. 2) are distributed almost exactly as expected, validating much of the methodology and analysis routines used in this work. Each plot demonstrates that the model that best fits the data according to the AIC and BIC is the model that was used to generate the simulations.
For the simulation, AIC and BIC differences fall almost entirely on the side of the dotted lines. As noted in Sec. 3.2, the AIC differences between the and models very closely follow the distribution, which is drawn on the plot as a solid curved line. Table 1 shows that 18.5 of the AIC differences were below zero (with expected from the approximation) and 3.5% of the BIC differences were below zero (with 2.6% expected), and were below the approximate 5% lower CI. These values were very similar for the differences of the and models for the simulation.
These observed percentages are close to the expected rates, but they differ because (1) the form assumes a large sample size and is only approximate and (2) the ML LLR found by the ordinal regression algorithm is also only approximate. The agreement between the approximation and the observed rates is sufficient for the purpose of determining which model is most appropriate for a single ROC curve fit. However, when we calculate an overall value for a study based on the sum of many LLRs, the discrepancy can lead to abnormally small values. For example, the sum of all 4010 LLRs between the and models for the simulation is 4509, which when computed as a deviate of the distribution has a cumulative probability of . To avoid this problem when calculating the overall value for each study, we correct the degrees of freedom by the factor , as described at the end of Sec. 3.2. For the model comparison, this correction factor is 1.05. These corrections force an overall value of 1/2 for the model-specific simulation studies in Table 2.
Table 2.
This table gives the overall adjusted values for each study. Under the null hypothesis that the data come entirely from the one-parameter model rather than the two-parameter model, these values would be uniformly distributed. The values were adjusted such that the daggered cells are 1/2. Starred 0. values are .
| Models | Sim | Sim | VCRS | DBTRS | VDTRS | DRRS | BMRS | MRIRS |
|---|---|---|---|---|---|---|---|---|
| 0.494† | ||||||||
| 0.500† | 0.017 | 0.751 | 0.979 | 0.101 | 0.985 |
5.1.2. Reader data
The lower six plots in Fig. 2 show the distributions of differences of the AIC and BIC for the human observer studies. For the digital breast tomosynthesis reader study (DBTRS), the digital resolution reader study (DRRS), and the magnetic resonance image reader study (MRIRS), the bulk (70 to 90%) of the AIC differences between the two-parameter models ( and ) and the one-parameter bi-normal model () are negative, so AIC implies that and are superior choices to . However, the BIC differences, which penalize the extra parameter more strongly than AIC, split across the zero line, favoring the two-parameter models for some observers, but not for others. Both AIC and BIC differences between the two-parameter models ( and ) and the one-parameter power-law model () are largely positive. Indeed, the DBTRS, DRRS, and MRIRS distributions look very similar to the simulated distributions. Likewise Table 1 shows that the two-parameter models are preferred at very similar rates in the real and simulated studies. In a model selection scenario or hypothesis testing scenario, we would select a less parsimonious two-parameter model for almost none of the data sets from these studies.
AIC implies that the volumetric detection tasks reader study (VDTRS) and the breast mass reader study (BMRS) favor single-parameter models ( and ) over two-parameter models in general. BIC shows an even stronger preference for single-parameter models. There is no clear preference between the single-parameter models, with the table showing that the AIC and BIC prefer to for of the fits. Table 1 demonstrates that in a hypothesis test only 10% of the data sets would be assigned the less parsimonious two-parameter model over the model.
The virtual colonoscopy reader study (VCRS) is more ambiguous. Most of the difference distributions are bimodal. All criteria show a strong preference for the model for some data sets. The ROC curves for this study (not shown) demonstrate the model’s ability to form large hooks that fit certain readers’ data very well. Some fits in this study were degenerate. This is also the only study that shows a clear preference of one two-parameter model () over the other ().
Table 2 gives the overall adjusted values for each study. Because of the low probabilities in the row, we see that there is some evidence in each reader study that the model is not sufficient for fitting all the curves in that study. The second row shows us that in four of the six reader studies, there is no statistically significant evidence of using a model less parsimonious than the model for any of the model fits. While the majority of ROC curves from VCRS and VDTRS are sufficiently fit by the model as determined by most criteria (Table 1), the studies have some very extreme observer data sets (VCRS) or a very large sample size (VDTRS) that make the detection of observers with non- curves possible.
5.1.3. CAD observers
Table 3 gives the differences in the AIC between models for the CAD observers. For both CAD data sets, the differences in AIC showed a preference for the two-parameter models over the single-parameter bi-normal model. However, the power-law model was even more preferred, with AIC values 1.5 to 2 units below the two-parameter models. Differences in BIC values were even larger, and values for the LRT between the and models were 0.89 and 0.51 for the M-CAD and S-CAD, respectively, indicating no evidence of a model less parsimonious than .
Table 3.
Differences in the AIC values between models for the computer-aided diagnostic (CAD) observers. Larger values indicate superiority of the second model in each pair.
| M-CAD | 3.00 | 2.11 | 1.98 | |||
| S-CAD | 5.85 | 1.73 | 1.57 |
5.2. Cross-Validation
The Monte Carlo cross-validation results are similar to the results using the information criteria. Figure 3 gives the normalized average likelihoods from the held-out data for each of the four models for each study.
As expected, the models from which the data were simulated gave the best cross-validation results. While the two-parameter models fit the data as well as the single-parameter models, they often overfit the training data, leading to a lower likelihood on the held-out data.
For VDTRS and BMRS, the model was superior, closely followed by the model. The model was superior for the VCRS study, with the superior for all rational concave ROC models. VCRS is the only study where cross-validation indicated a preference for a less parsimonious two-parameter model. The model was superior for all other data sets tested. Based on this sample of studies, we would first consider the power-law model when presented with a new set of data.
6. Discussion
6.1. Power-Law Model
Overall, our results show that the power-law model fits reader study data better than other models investigated. This is also true of the artificial CAD observers. This result has also been noted with several other study data sets that are not provided here. Therefore, in this discussion, we further examine the properties of the power-law model. While the two-parameter models almost always attained higher likelihoods than the power-law model, the AIC, BIC, and cross-validation indicate that the extra parameter is not usually needed. Models with more parameters may be justified for larger data sets, but not for most of the typically sized sets presented here.
DeCarlo12 points out that these power-law distributions are minimum value distributions. This can be seen as follows. , where is the probability that the ’th latent signal-present rating is greater than . If the observations are independent, then is the probability that all the values are greater than and the probability that the minimum observation is greater than . So the signal-absent distribution, is distributed as the minima of signal-present observations. Therefore, one interpretation of the power-law model is that readers give scores to signal-absent images that are distributed as the minima of a certain number () of signal-present images.
6.2. Comparison with Other Models
6.2.1. Bi-normal model and the mean-to-sigma ratio
When analyzing data with the bi-normal model, previous authors31 have demonstrated that the slopes and intercepts of ROC curves on a normally transformed scale are not the same for different perceptual tasks. But authors have found that the estimated mean-to-sigma ratio, , of a large number of perceptual tasks is roughly constant,3,14,32 with and defined in Eq. (1). The mean-to-sigma ratio is defined as the difference in means divided by the difference in standard deviations.33 These authors point out that the ratio is between 3 and 5, roughly 4, and is constant across a range of AUC values.
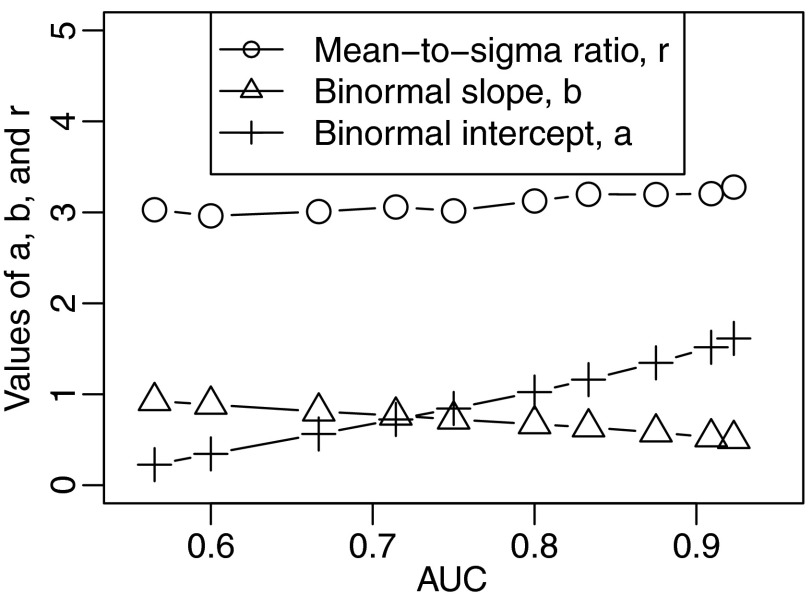
To compare the bi-normal model to the power-law model, we fit the bi-normal model to very large simulated power-law data sets with 40,000 observations. Estimates of the parameters and from these fits give a bi-normal model that, in some sense, best mimics the corresponding power-law model. The estimates , the intercept of the bi-normal ROC curve, , the slope of the bi-normal ROC curve, and , the mean-to-sigma ratio, are shown for a range of AUC values in Fig. 5. The values of and vary with AUC, but is fairly constant with a value of . The power-law model gives a mean-to-sigma ratio that is constant across AUC values, just like findings of authors of other studies.
Fig. 5.
Maximum likelihood estimates of parameters of the bi-normal model from fits to very large power-law data sets as a function of the AUC value from which those data sets were drawn. The parameters are the mean-to-sigma ratio [], the intercept of the bi-normal ROC curve (), and the slope of the bi-normal ROC curve (). Across very different AUC values, the mean-to-sigma ratio remains nearly constant, .
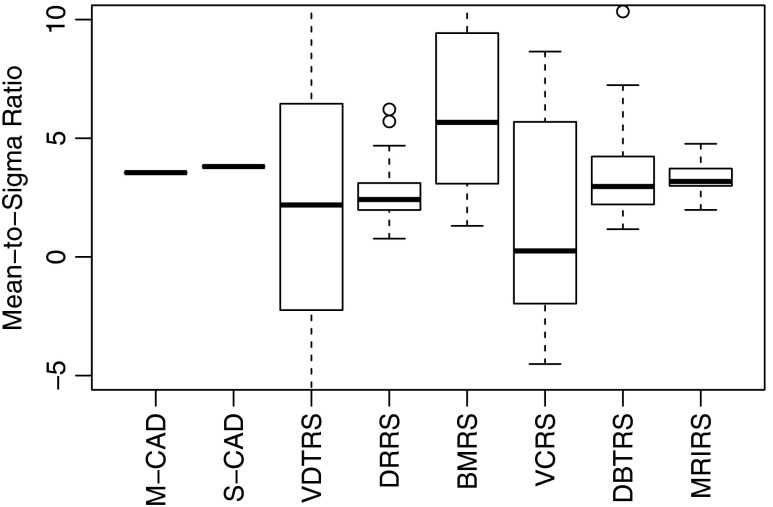
Figure 6 displays box plots representing the distribution of for each of the different featured studies. Due to the difference in the denominator of the mean-to-sigma ratio, its value is highly variable, particularly on small data sets. For this reason, our figure does not show all whiskers or outliers in the plot, only the centers of the distributions. Our data are consistent with other reported mean-to-sigma ratios. The median of all the data is 3.0 and the mean is 3.1. The mean-to-sigma ratio fit from power-law data in the previous paragraph is consistent with the average bi-normal mean-to-sigma ratio of our sample of studies and is consistent with the measured values of other authors. Therefore, it is likely that the power-law model would fit data well from many other studies.
Fig. 6.
Box plots of the distributions of the mean-to-sigma ratio for each study in the paper. Not all whiskers or outliers are visible.
6.2.2. Maximum signal model
Under the argument that images consist of a number of visual stimuli, and that observers give their rating to the most obvious signals or targets in an image, the distributions of signal-absent ratings and signal-present ratings should be distributed as
| (10) |
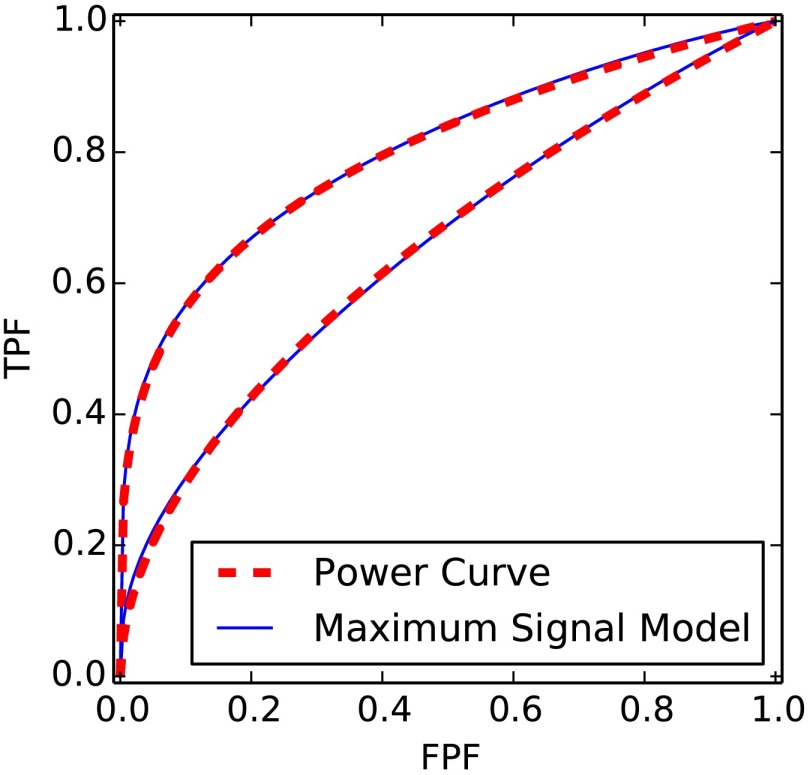
where is the normal cumulative distribution function and the assumed distribution of the individual stimuli.33,34 For , the model is an equal variance bi-normal model where . At moderately large (), this model becomes similar to a power-law model in the shape of the ROC curve for a wide range of . The similarity of the power-law and maximum-signal models is shown in Fig. 7 for a typical range of AUC values.
Fig. 7.
Comparisons of the ROC curves of the power-law model and the maximum signal model for as discussed in Sec. 6.2.2.
6.3. Summary
Semiparameteric models for ROC curves are frequently used to fit data from observer studies in medical imaging. These models may be more powerful than or complementary to nonparametric methods. Few comparisons of these semiparametric models using standard statistical techniques are known in the literature. This paper made such comparisons on a sample of published imaging studies.
We found that the single-parameter power-law model fits the data from many signal-detection reader studies well. For many data sets in medical imaging, less parsimonious models with additional parameters are not justified based upon cross-validation or AIC or BIC. In the majority of studies that we examined, there was no statistical evidence that more complex models should be used. The form of the power-law model is consistent with other models and data sets found in the literature.
Acknowledgments
We wish to thank all those who collected or provided anonymous reader data sets to us: Asli Kumcu, Nicholas Petrick, Berkman Sahiner, Heang-Ping Chan, Jianhua Yao, Loren Niklason, Elizabeth Rafferty, and Caroline VanDyke. We thank Jovan Brankov for his useful suggestions. We are also deeply indebted to Robert Wagner for his guidance in the field of medical image evaluation at the FDA.
Biographies
Frank W. Samuelson is a physicist at the U.S. Food and Drug Administration. He received his AB in physics from Harvard University and a PhD from Iowa State University in astrophysics. He was a fellow at Los Alamos National Laboratory before joining the FDA under Robert Wagner. His current research interests include the evaluation of medical imaging devices.
Xin He is a senior staff fellow at the U.S. Food and Drug Administration. She received her BS in engineering physics from Tsinghua University in China and her PhD from University of North Carolina at Chapel Hill in biomedical engineering. She is interested in developing laboratory performance evaluation methods that predict clinical performance.
References
- 1.Wagner R. F., Metz C. E., Campbell G., “Assessment of medical imaging systems and computer aids: a tutorial review,” Acad. Radiol. 14(6), 723–748 (2007). 10.1016/j.acra.2007.03.001 [DOI] [PubMed] [Google Scholar]
- 2.Dorfman D. D., Alf E., “Maximum likelihood estimation of parameters of signal detection theory and determination of confidence intervals—rating method data,” J. Math. Psychol. 6(3), 487 (1969). 10.1016/0022-2496(69)90019-4 [DOI] [Google Scholar]
- 3.Green D. M., Swets J. A., Signal Detection Theory and Psychophysics, John Wiley & Sons, New York: (1966). [Google Scholar]
- 4.Egan J. P., Signal Detection Theory and ROC Analysis, Academic Press, New York: (1975). [Google Scholar]
- 5.Dorfman D. D., et al. , “Proper receiver operating characteristic analysis: the bigamma model,” Acad. Radiol. 4(2), 138–149 (1997). 10.1016/S1076-6332(97)80013-X [DOI] [PubMed] [Google Scholar]
- 6.Metz C. E., Pan X., “Proper binormal ROC curves: theory and maximum-likelihood estimation,” J. Math. Psychol. 43(1), 1–33 (1999). 10.1006/jmps.1998.1218 [DOI] [PubMed] [Google Scholar]
- 7.Dorfman D. D., Berbaum K. S., Brandser E. A., “A contaminated binormal model for ROC data. Part II. A formal model,” Acad. Radiol. 7(6), 427–437 (2000). 10.1016/S1076-6332(00)80383-9 [DOI] [PubMed] [Google Scholar]
- 8.Qin J., Zhang B., “Using logistic regression procedures for estimating receiver operating characteristic curves,” Biometrika 90(1), 585–596 (2003). 10.1093/biomet/90.3.585 [DOI] [Google Scholar]
- 9.Gur D., Bandos A. I., Rockette H. E., “Comparing areas under receiver operating characteristic curves: potential impact of the ‘last’ experimentally measured operating point,” Radiology 247(1), 12–15 (2008). 10.1148/radiol.2471071321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Burnham K. P., Anderson D. R., Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach, Springer, New York: (2002). [Google Scholar]
- 11.Wandell B., Luce R. D., “Pooling peripheral information: averages versus extreme values,” J. Math. Psychol. 17(3), 220–235 (1978). 10.1016/0022-2496(78)90017-2 [DOI] [Google Scholar]
- 12.DeCarlo L. T., “Signal detection theory and generalized linear models,” Psychol. Methods 3(2), 186–205 (1998). 10.1037/1082-989X.3.2.186 [DOI] [Google Scholar]
- 13.Egan J. P., Greenberg G. Z., Schulman A. I., “Operating characteristics, signal detectability, and the method of free response,” J. Acoust. Soc. Am. 33(8), 993–1007 (1961). 10.1121/1.1908935 [DOI] [Google Scholar]
- 14.Swets J. A., “Indices of discrimination or diagnostic accuracy: their ROCs and implied models,” Psychol. Bull. 99(1), 100–117 (1986). 10.1037/0033-2909.99.1.100 [DOI] [PubMed] [Google Scholar]
- 15.Hanley J. A., McNeil B. J., “The meaning and use of the area under the receiver operating characteristic (ROC) curve,” Radiology 143(1), 29–36 (1982). 10.1148/radiology.143.1.7063747 [DOI] [PubMed] [Google Scholar]
- 16.Gumbel E., Statistics of Extremes, Columbia University Press, New York: (1958). [Google Scholar]
- 17.Tosteson A. N. A., Begg C. B., “A general regression methodology for ROC curve estimation,” Med. Decis. Making 8(3), 204–215 (1988). 10.1177/0272989X8800800309 [DOI] [PubMed] [Google Scholar]
- 18.Metz C. E., Herman B. A., Shen J.-H., “Maximum likelihood estimation of receiver operating characteristic (ROC) curves from continuously-distributed data,” Stat. Med. 17(9), 1033–1053 (1998). 10.1002/(ISSN)1097-0258 [DOI] [PubMed] [Google Scholar]
- 19.Samuelson F. W., “Two-sample models with monotonic likelihood ratios for ordinal regression,” J. Math. Psychol. 55, 223–228 (2011). 10.1016/j.jmp.2011.01.001 [DOI] [Google Scholar]
- 20.Akaike H., “A new look at the statistical model identification,” IEEE Trans. Automat. Contr. 19(6), 716–723 (1974). 10.1109/TAC.1974.1100705 [DOI] [Google Scholar]
- 21.Schwarz G., “Estimating the dimension of a model,” Ann. Stat. 6(2), 461–464 (1978). 10.1214/aos/1176344136 [DOI] [Google Scholar]
- 22.Wilks S. S., “The large-sample distribution of the likelihood ratio for testing composite hypotheses,” Ann. Math. Stat. 9(1), 60–62 (1938). 10.1214/aoms/1177732360 [DOI] [Google Scholar]
- 23.Dorfman D. D., Berbaum K. S., Metz C. E., “Receiver operating characteristic rating analysis: generalization to the population of readers and patients with the jackknife method,” Invest. Radiol. 27(9), 723–731 (1992). 10.1097/00004424-199209000-00015 [DOI] [PubMed] [Google Scholar]
- 24.Petrick N., et al. , “CT colonography with computer-aided detection as a second reader: observer performance study,” Radiology 246(1), 148–156 (2008). 10.1148/radiol.2453062161 [DOI] [PubMed] [Google Scholar]
- 25.Rafferty E. A., et al. , “Assessing radiologist performance using combined digital mammography and breast tomosynthesis compared with digital mammography alone: results of a multicenter, multireader trial,” Radiology 266(1), 104–113 (2013). 10.1148/radiol.12120674 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Platiša L., et al. , “Volumetric detection tasks with varying complexity: human observer performance,” Proc. SPIE 8318, 83180S (2012). 10.1117/12.911558 [DOI] [Google Scholar]
- 27.Chan H. P., et al. , “Digital mammography: observer performance study of the effects of pixel size on the characterization of malignant and benign microcalcifications,” Acad. Radiol. 8, 454–466 (2001). 10.1016/S1076-6332(03)80616-5 [DOI] [PubMed] [Google Scholar]
- 28.Sahiner B., et al. , “Multi-modality CADx: ROC study of the effect on radiologists accuracy in characterizing breast masses on mammograms and 3d ultrasound images,” Acad. Radiol. 16(7), 810–818 (2009). 10.1016/j.acra.2009.01.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.VanDyke C. W., et al. , “Cine MRI in the diagnosis of thoracic aortic dissection,” presented at 79th Annual Meeting of the Radiological Society of North America, Radiological Society of North America, Chicago, Illinois: (1993). [Google Scholar]
- 30.Burns J., et al. , “Automated detection of sclerotic metastases in the thoracolumbar spine on computed tomography,” Radiology 268(1), 69–78 (2013). 10.1148/radiol.13121351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Swets J. A., “Form of empirical ROCs in discrimination and diagnostic tasks: implications for theory and measurement of performance,” Psychol. Bull. 99(2), 181–198 (1986). 10.1037/0033-2909.99.2.181 [DOI] [PubMed] [Google Scholar]
- 32.Hillis S. L., Berbaum K. S., “Using the mean-to-sigma ratio as a measure of the improperness of binormal ROC curves,” Acad. Radiol. 18(2), 143–154 (2011). 10.1016/j.acra.2010.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Swets J. A., Tanner W. P., Birdsall T. G., “Decision processes in perception,” Psychol. Rev. 68(5), 301–340 (1961). 10.1037/h0040547 [DOI] [PubMed] [Google Scholar]
- 34.Pelli D. G., “Uncertainty explains many aspects of visual contrast detection and discrimination,” J. Opt. Soc. Am. A 2(9), 1508–1532 (1985). 10.1364/JOSAA.2.001508 [DOI] [PubMed] [Google Scholar]