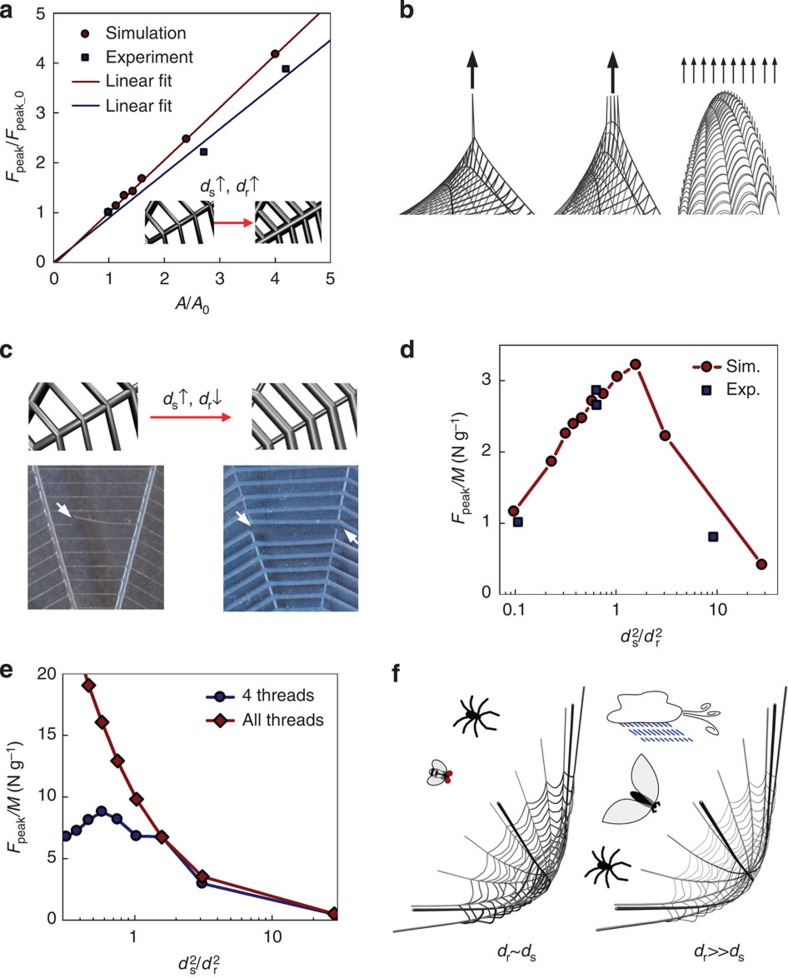
Figure 4. Material distribution effects on web strength.

(a) Effect of homogeneously increasing thread diameters on PDMS web strength. We take the initial structure of d_{s_0}=200 μm and d_{r_0}=250 μm and keep d_s/d_r=0.8 constant for different models with increasing diameters for both threads. The peak force is normalized by the peak force of the initial web structure (F_{peak_0}=0.3 N). Linear fitting gives F_peak/F_{peak_0}=(1.03±0.01)A/A₀ for simulation and F_peak/F_{peak_0}=(0.89±0.12)A/A₀ for experiment. (b) Close-up of the simulation snapshots of applying point force (n=1) (left), force involves four spiral threads (n=4) (middle), and homogenously distributed force (force on each section of each thread is proportional to its cross-section area) to the web (right). For the third case, considering that a web usually does not subject to wind and rain loading normal to the web surface, the web is initially tilted at an angle of ϕ=26.6° with the distributed force. (c) Different failure modes for webs with d_s²/d_r² changing from 0.1 to 10 for point loading. The web with d_s²/d_r²=0.1 ruptures at the loading point while the web having d_s²/d_r²=10 ruptures in the radial threads away from loading. (d) Comparison between simulation and experiment of F_peak/M as a function of d_s²/d_r². The peak value of 3.2 N g⁻¹ is reached at d_s/d_r=1.26. (e) Simulation result of F_peak/M for the case n=4 and homogenously distributed force. Maximum F_peak/M=8.8 N g⁻¹ is reached at d_s/d_r=0.76. No peak value is identified for homogenously distributed loading, but F_peak/M increases for decreasing d_s/d_r. At d_s/d_r→0, the maximum F_peak/M is estimated as 140 N g⁻¹ for the strength of the 12 radial threads. (f) Schematics of the optimized spider web in different conditions. d_s∼d_r is for the case of small prey and self-weight, while d_r>>d_s is necessary for large prey and rain and wind that can cause homogenously distributed force.