Algorithm 1. Normalized DTW distance.
Let x, y ∈ 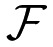be two finite sequences of lengths N = |x| and M = |y| , respectively. The normalized DTW distance Δ(x, y) is computed as follows:
1.	Initialize δ(0,0) = 0, δ(n,0) = ∞ for n = 1,…, N and δ(0,m) = ∞ for m = 1,…, M and compute the terms of the DTW matrix, using the difference equation:
	δ(n, m) = min {δ(n−1,m), δ(n,m−1), δ(n−1,m−1)} + d(xn, xm)
	for (n, m) ∈ {1,…, N} × {1,…, M}.
2.	Initialize ℓ = 0, vℓ = (N, M) and compute the sequence v ∈ ℕ2 as follows:
	while [vℓ ≠ (1,1)], repeat:
	ℓ = ℓ + 1,
	vℓ ∈ argmin{δv : v ∈ {vℓ−1 − (1,0), vℓ−1 − (0,1), vℓ−1 − (1,1)}}
	end while loop
	then K = |v| and w* = {wℓ : wℓ = sK−ℓ +1(v)}.
3.	The normalized DTW distance between the sequences x and y is Δ(x, y) = k−1δ(N,M).