|
| |||||||||
| Algorithm 3. Evolving self-organizing map. | |||||||||
|
| |||||||||
| 1. | Start with k = 0,
 = ∅, = ∅,
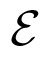 = ∅. = ∅. |
||||||||
| 2. | Choose a new x ∈ Σ and compute:
 m(x) = ∅ go to 4. m(x) = ∅ go to 4. |
||||||||
| 3. | Update:
|
||||||||
| 4. | Let y* be such that:
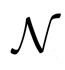 (y*) = {y : (y,y*) ∈ (y*) = {y : (y,y*) ∈
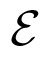 }. Update: }. Update:
|
||||||||
| 5. | Update the connection strengths as follows:
 ′ × ′ ×
 ′ and i ≠ j. ′ and i ≠ j. |
||||||||
| 6. | Do k′ = k + 1; if mod (k′, τ) = 0, remove the weakest connection. | ||||||||
| 7. | Do k = k′,
 = =
 and and
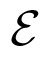 = =
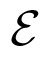 , and go to 2. , and go to 2. |
||||||||
|
| |||||||||

An official website of the United States government
Here's how you know
Official websites use .gov
A
.gov website belongs to an official
government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you've safely
connected to the .gov website. Share sensitive
information only on official, secure websites.