Broadband surface-wave transformation cloak

Significance

Guiding surface electromagnetic waves around disorder without disturbing the wave amplitude or phase is in great demand for modern photonic and plasmonic devices. In this work, we introduce a class of cloaks capable of remarkable broadband surface electromagnetic waves guidance around ultrasharp corners and bumps with no perceptible changes in amplitude and phase. This work provides strong support for the application of transformation optics to plasmonic circuits and could pave the way for high-performance, large-scale integrated photonic circuits.

Abstract

Guiding surface electromagnetic waves around disorder without disturbing the wave amplitude or phase is in great demand for modern photonic and plasmonic devices, but is fundamentally difficult to realize because light momentum must be conserved in a scattering event. A partial realization has been achieved by exploiting topological electromagnetic surface states, but this approach is limited to narrow-band light transmission and subject to phase disturbances in the presence of disorder. Recent advances in transformation optics apply principles of general relativity to curve the space for light, allowing one to match the momentum and phase of light around any disorder as if that disorder were not there. This feature has been exploited in the development of invisibility cloaks. An ideal invisibility cloak, however, would require the phase velocity of light being guided around the cloaked object to exceed the vacuum speed of light—a feat potentially achievable only over an extremely narrow band. In this work, we theoretically and experimentally show that the bottlenecks encountered in previous studies can be overcome. We introduce a class of cloaks capable of remarkable broadband surface electromagnetic waves guidance around ultrasharp corners and bumps with no perceptible changes in amplitude and phase. These cloaks consist of specifically designed nonmagnetic metamaterials and achieve nearly ideal transmission efficiency over a broadband frequency range from 0⁺ to 6 GHz. This work provides strong support for the application of transformation optics to plasmonic circuits and could pave the way toward high-performance, large-scale integrated photonic circuits.

One of the main limitations in plasmonic circuitry and devices (1, 2) that use surface electromagnetic waves (surface plasmons at optical frequencies) as information and energy carriers is the inability to perfectly guide surface electromagnetic waves around unavoidable disorders, such as sharp corners. Although near-perfect transmission around sharp corners in electronic circuits is routine, it is fundamentally difficult to realize with surface waves, because surface waves suffer from scattering loss when encountering sharp corners or other irregular disorders.

Scattering-free guidance of surface waves around sharp corners has been shown only in topological electromagnetic surface states (3–7). It has been developed in analogy with electronic chiral edge states in quantum Hall systems (8) and topological insulators (9, 10). To force the waves to circumvent disorders, the studies cited above typically require the use of photonic crystals with substantial magnetic responses (11). The use of magnetic metamaterials limits these realizations to a narrow-microwave frequency band. The use of conventional nonmagnetic photonic materials, however, could allow for scalability to the optical regime with broad bandwidth.

The difficulty in sharp bending is the dramatic momentum mismatch of surface electromagnetic waves before and after passing the sharp corner in an extremely compact space. Transformation optics (12, 13) allow for the design of inhomogeneous metamaterials that control light by effectively warping the electromagnetic space analogously to the way that gravity curves space in general relativity. Because the concept of momentum stems essentially from space homogeneity (14), an effectively curved electromagnetic space provides a method to match wave momenta by compensating for the asymmetry of spatial translation around sharp corners. Surface electromagnetic waves can be, thereby, deceived that they are still propagating along a flat surface without any corners.

In the past few years, transformation optics has been used to develop invisibility cloaks to hide objects from free-space propagating electromagnetic waves (15–23). An ideal invisibility cloak is a fundamentally narrow band, because it would require the phase velocity of light being guided around the “cloaked object” to exceed the vacuum speed of light (13, 15, 24). However, surface electromagnetic waves are essentially slow waves, with bending that will not cause superluminal propagation in the majority of situations, but all of the potential applications of transformation optics in surface electromagnetic waves (25–29) so far are still theoretical. Most theoretical designs only deal with objects with relatively smooth surfaces or finite bending radii (25, 26). Refs. 28 and 29 proposed alternative surface wave-bending approaches; however, in general, scattering will occur when an ultrasharp bending with zero radius is desired. Therefore, if a similar approach of sharp bending could be realized for surface waves, many unique conceivable applications would become feasible: not only waveguides for sharp right-angle corners (3) but also, carpet cloaks that can hide irregular bumps on the metal–dielectric interface (26), super plasmonic resonators with extremely high Q values (30), etc.

Here, we present experimental demonstration of broadband sharp bending of surface electromagnetic waves with almost ideal transmission, which allows “invisibility cloaking” of disorders, such as ultrasharp corners and bumps for surface electromagnetic waves. The remarkable broadband guidance, lacking in previous scattering-free topological electromagnetic surface states and free-space invisibility cloaks, is because of two reasons. First, the slow-wave property of surface electromagnetic waves can overcome the bottleneck of free-space invisibility cloaks, because its phase velocity does not need to exceed the vacuum speed of light. Second, we adopt a fully nonmagnetic design with naturally accessible dielectric parameters, whereas magnetic responses were necessary to open the topological band gap for topological electromagnetic surface states.

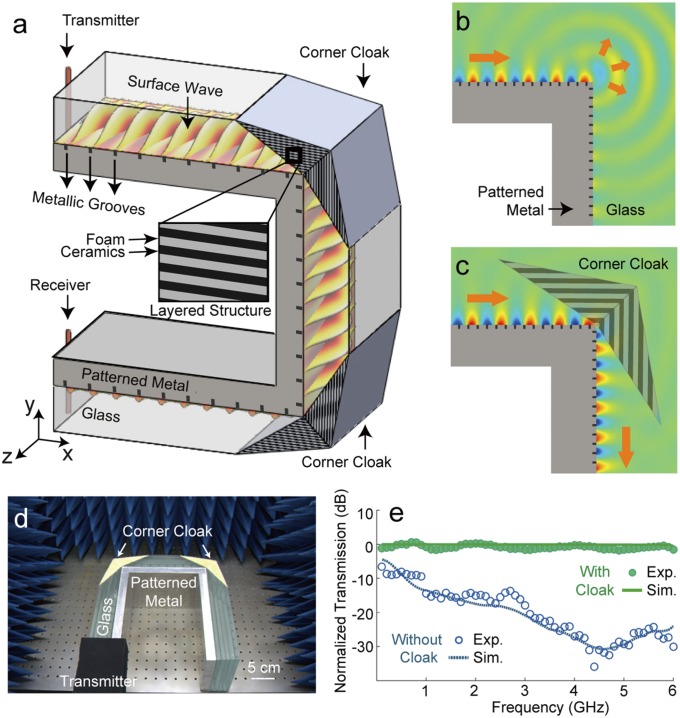
We start with the demonstration of bending a surface electromagnetic wave across sharp right-angle corners at microwave frequencies—similar to the previous demonstration of bending a guided topological surface electromagnetic wave in a photonic crystal (3). We call the bending adaptor a “corner cloak,” because it effectively hides a corner to the wave as if the corner did not exist. Because metals at microwave frequencies are perfect electric conductors that generally do not support surface electromagnetic waves, here we adopt the approach of geometrically induced or spoof surface plasmons (31) [i.e., we use a grooved metallic surface (referred to as a patterned metal in Figs. 1–3) to support surface electromagnetic waves in the microwave regime]. Fig. 1A shows the experimental setup: a U-shaped surface-wave waveguide (a metal base with periodic grooves on its surfaces; i.e., the patterned metal) with two right-angle zero-radius corners. Given the sizes of the cloaks, the more confined the surface waves on the dielectric–metal interface, the better the cloaking performance. To enhance the confinement, we load the grooves with ceramic material with permittivity ε_ceramic = 21. We use glass with permittivity ε_b = 4.6 as the surrounding background that is to be impedance-matched with the cloaks. More details can be found in Fig. S1 and SI Methods.

Fig. 1.

Surface-wave bending around sharp corners. (A) A U-shaped surface-wave waveguide with grooves on its surface covered by glass is illuminated by a dipole antenna. The two sharp corners are covered by two corner cloaks (i.e., layered structures with subwavelength foam and ceramic materials). A second dipole antenna located at the output of the waveguide measures the transmission. (B) Simulation of a surface wave when it encounters a sharp corner that is not covered by a cloak. (C) Simulation of a surface wave when the sharp corner is cloaked by a corner cloak. (D) Photo of a fabricated model. The transmitter is shielded by the microwave absorber material. (E) Measured normalized transmission of surface waves through the waveguide. Exp., experimental data; Sim., simulation data.

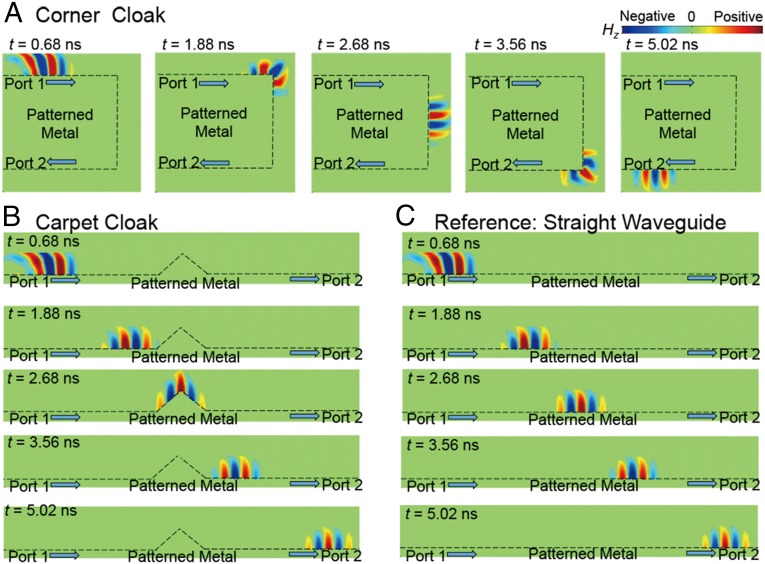
Fig. 3.

A Gaussian-shaped pulse propagates on the patterned metal. A point source (port 1) generates the pulse at 0 ns. The bandwidth of the pulse is 6 GHz, and the center frequency is 3 GHz. The magnetic field distributions for three cases [(A) the corner cloaks, (B) the carpet cloak, and (C) the straight waveguide reference] are plotted to show the propagation of the pulse at five equivalent temporal sampling points.

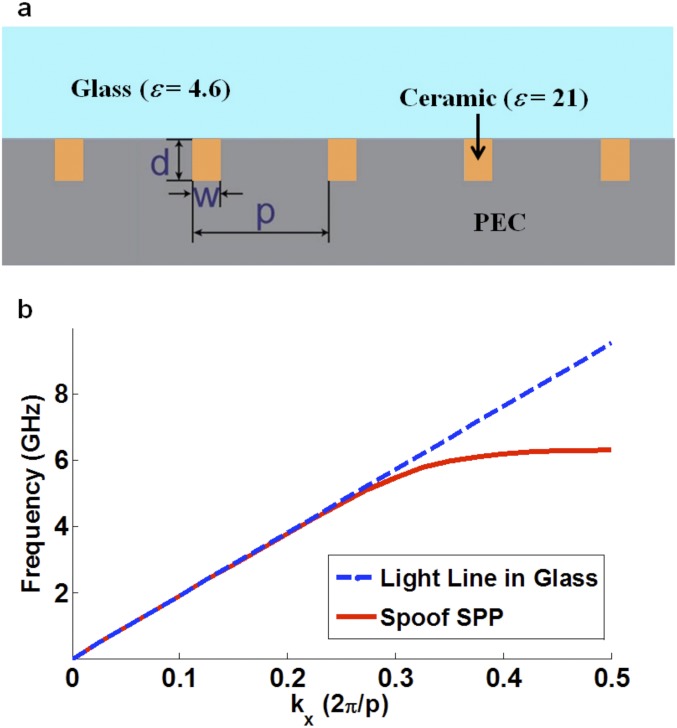
Fig. S1.

Dispersion relation of spoof surface plasmons on the metallic grooved structure. (A) Schematic diagram of the metallic grooves. (B) Dispersion relation of spoof surface plasmons for d = 2.3 mm, w = 1.5 mm, and p = 7.5 mm. PEC, perfect electric conductor; SPP, surface plasmon.

The two identical corner cloaks locate at the two corners. This structure that consists of the U-shaped waveguide and two corner cloaks can be thought of as if it were transformed from a straight waveguide without any corner. A corner cloak, when transformed back, corresponds to a triangular space on top of the dielectric–metal interface, which has an area that is purposely chosen to be the same as the corner cloak. This area preservation guarantees nonmagnetism in the cloak design for surface electromagnetic waves (more details are in Fig. S2 and SI Methods). The two identical corner cloaks require anisotropic constitutive parameters. For each cloak, the required principal permittivities in two orthogonal directions, ε₁ and ε₂, after the procedure of diagonalization, where only components in the xy plane are relevant, are ε₁ = 10.7 and ε₂ = 2.0. These cloaks were implemented with a metamaterial consisting of a stack of the following two materials with subwavelength thicknesses: a microwave dielectric ceramic with permittivity ε_ceramic = 21 (Wuxichaoying K-21; loss tangent: $\hspace{0.17em}1\times {10}^{-4}$; 1-mm thickness) and a polymer foam with permittivity ε_foam = 1.1 (Rohacell 71HF; loss tangent:$\hspace{0.17em}16\times {10}^{-4}$; 1.06-mm thickness). According to the standard formulas of effective medium theory, one can get

$$\{\begin{array}{c}{\epsilon }_1=r{\epsilon }_{ceramic}+\left(1-r\right){\epsilon }_{foam}\\ \frac{{\epsilon }_2={\epsilon }_{ceramic}{\epsilon }_{foam}}{\left[\left(1-r\right){\epsilon }_{ceramic}+r{\epsilon }_{foam}\right]}\end{array},$$

where the filling factor is given by $r=0.485$. Fig. 1B shows the simulation of the transmission of surface electromagnetic waves when the corners are not cloaked by the corner cloaks; a dramatic scattering loss is evident. However, the transmission of surface electromagnetic waves across a sharp corner is perfect when both corners are cloaked by corner cloaks (Fig. 1C).

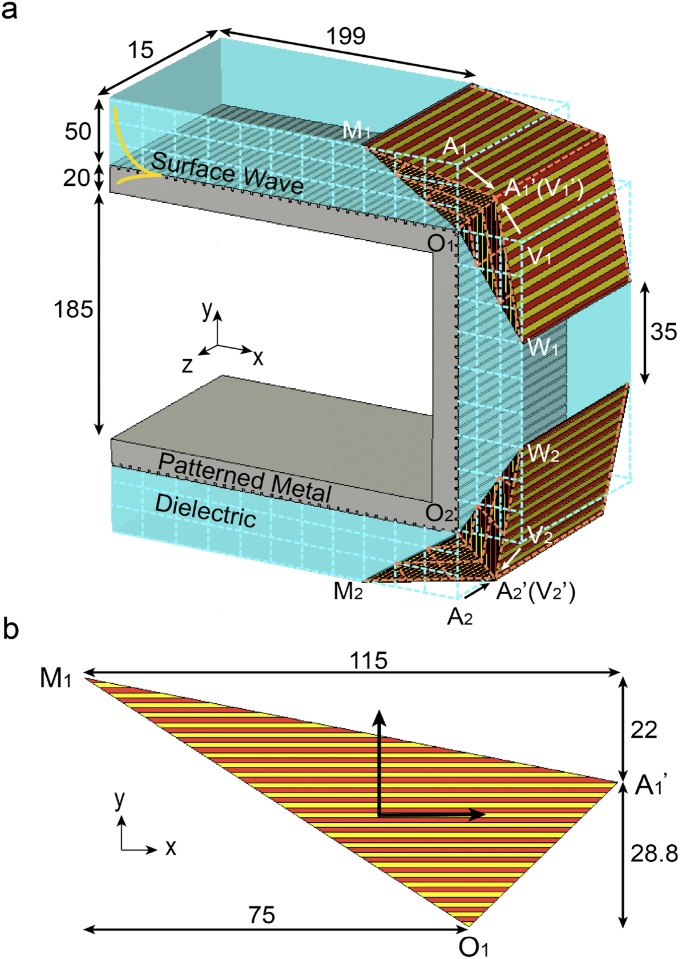
Fig. S2.

Design of the transformation optics corner cloaks for sharp bending of electromagnetic surface waves. (A) The 3D scheme of the U-shaped surface-wave waveguide. The materials in red, yellow, and blue are microwave ceramic, dielectric foam, and low-loss glass, respectively. The areas of the regions $M_n{O}_n{A}_n$ and $W_n{O}_n{V}_n$ (before the transformation) are preserved over the transformation to $M_n{O}_n{A\prime }_n$ and $W_n{O}_n{V\prime }_n$, respectively, where the subscript n indicates the nth sharp corner. The mesh shows the electromagnetic space above the metal–dielectric interface, whereas the electromagnetic space below the interface is neglected because of the shallow field penetration in metal. (B) Dimensions of the ceramic/foam-layered metamaterial structure. Four triangles of the metamaterial structure form two corner cloaks. All of the dimensions are in millimeters.

A fabricated model with two corner cloaks is shown in Fig. 1D. For comparison, we also fabricated a straight waveguide with similar grooves and the same total propagation distance. The transmission data measured on the U-shaped surface-wave waveguide from 0⁺ (100 MHz) to 6 GHz without/with corner cloaks are normalized to the transmission data measured on the straight waveguide (Fig. 1E). Without corner cloaks, the transmission measured at the output of the U-shaped waveguide is close to zero, but when both sharp corners are hidden by the corner cloaks, the transmission is almost unity. The experimental result shows near-perfect cloaking of two right-angle zero-radius corners for surface electromagnetic waves in a broad bandwidth from 0⁺ to 6 GHz (i.e., with a fractional bandwidth of 200%).

Next, we show a surface-wave carpet cloak used to cover an ultrasharp bump on a flat metal–dielectric interface. Fig. 2A shows our experimental setup. Like in the realization of the corner cloaks, we used a metal base with grooves to support surface electromagnetic waves. A sharp bump on the flat surface acts as an obstacle able to block the propagation of surface electromagnetic waves. The carpet cloak that can hide this sharp bump was designed with a similar transformation optics approach (more details can be found in Fig. S3 and SI Methods). The numerical simulation for the real structure in the presence of a sharp bump is shown in Fig. 2 B and C: without a carpet cloak, most of the wave energy is scattered into the background medium near the apex of the bump; when the carpet cloak is put on top of the bump, however, the electromagnetic surface waves can be smoothly guided around the bump and returned to their original path as if the bump was not there. A fabricated model with a carpet cloak implemented with the same metamaterial used in the corner cloaks is shown in Fig. 2D. The measured transmissions, normalized to the transmission through a straight waveguide without the bump, are shown in Fig. 2E. For the setup without a cloak, the normalized transmission is close to zero, indicating that the propagation of surface electromagnetic waves has been blocked by the bump. For the case with a carpet cloak, the normalized transmission approaches unity, showing near-perfect cloaking of a sharp bump for surface electromagnetic waves in a broad bandwidth from 0⁺ to 6 GHz.

Fig. 2.

Surface-wave carpet cloaking. (A) A straight surface-wave waveguide with a sharp bump is illuminated by a dipole antenna. The surface of the metal base is grooved similarly as that in Fig. 1A. The sharp bump is covered by a carpet cloak (i.e., a layered structure with subwavelength foam and ceramic materials). A second dipole antenna located at the output of the waveguide measures the transmission. (B) Simulation of a surface wave when it encounters the sharp bump without a carpet cloak. (C) Simulation of a surface wave when the sharp bump is cloaked by the carpet cloak. (D) Photo of a fabricated model. The transmitter is shielded by the microwave absorber material. (E) Measured normalized transmission of surface waves through the waveguide. Exp., experimental data; Sim., simulation data.

Fig. S3.

Design of the transformation optics carpet cloak that hides a sharp bump. (A) The 3D scheme of the carpet cloak and the grooved metallic base with a sharp bump. The materials in red, yellow, and blue are microwave ceramic, dielectric foam, and low-loss glass, respectively. The area of the region HIJK (before the transformation) is preserved over the transformation to HMIJNK. The mesh indicates the electromagnetic space above the metal–dielectric interface, whereas the electromagnetic space below the interface is neglected because of the shallow field penetration in metal. (B) Details of the ceramic/foam-layered metamaterial structure forming the carpet cloak. All of the dimensions are in millimeters.

A striking feature, absent in topological electromagnetic surface states, is that, when the surface waves are perfectly guided by the cloaks, the phase is preserved. We used a pulsed signal to show this behavior. Fig. 3 shows the dynamic propagation of a pulse through the cloaks, which was obtained with the commercial software COMSOL Multiphysics. A point source at port 1 excites a Gaussian-shaped pulse (bandwidth: 0⁺–6 GHz; center frequency: 3 GHz) at 0 ns. The magnetic field distributions are plotted to show the propagation of the pulse on the patterned metal for the setup with the corner cloaks (Fig. 3A), the carpet cloak (Fig. 3B), and a straight waveguide as a reference (Fig. 3C). For the realization with corner cloaks, the signal reaches the first and second sharp corners at 1.88 and 3.56 ns, respectively. At both sharp corners, the pulse signal is perfectly guided by the corner cloak, and at last, it leaves the patterned metal from port 2. In the case of the carpet cloak, the pulse reaches the bump at 2.68 ns, and it is guided smoothly across the bump by the carpet cloak without any loss. The pulse reaches the same positions as in the straight waveguide, with no relative delay, indicating that the phase is well-preserved in a broad bandwidth by the cloaks. Movies S1 and S2 show more details of the propagating pulse. Fig. 4 shows the measured phase for the corner cloak (Fig. 4A) and carpet cloak (Fig. 4B). The curves almost coincide with their references over the frequency band from 0⁺ to 6 GHz, confirming that the phase of the surface wave is well-preserved by the cloaks.

Fig. 4.

Phase measurements. (A) The corner cloaks. (B) The carpet cloak. The phases with the straight waveguide are plotted for reference. In both cases, the phase curves almost coincide with their references over the frequency band from 0⁺ to 6 GHz.

The above results show scattering-free guidance of surface electromagnetic waves around large disorders, with both wave energy and phase undisturbed in a 200% broad-frequency band. Switching from free-space electromagnetic waves to surface electromagnetic waves, transformation cloaks can find immediate applications without any fundamental limitations. The fully nonmagnetic design makes it feasible to further extend to higher frequencies and/or conventional surface waves. Our work, thereby, paves the way for the next generation of photonic and plasmonic devices, allowing for flexible design without concern in disorders.

SI Methods

Dispersion Relation of Spoof Surface Plasmons on the Metallic Grooved Structure Used in Our Models.

Fig. S1A shows the perfect electric conductor surface with a 1D periodic array of grooves with periodicity p. Each groove has width w and depth d. All grooves are filled with a ceramic material with permittivity ε_ceramic = 21. The background material above the grooved structure is glass, with ε_b = 4.6. Fig. S1B shows the simulated dispersion relation of spoof surface plasmons for d = 2.3 mm, w = 1.5 mm, and p = 7.5 mm.

Specifications of the U-Shaped Waveguide and the Corner Cloaks.

Here, we briefly introduce the transformation design. Fig. S2A shows the 3D scheme of the U-shaped waveguide with sharp corners and periodic grooves. The layered metamaterial structure is a stack of Rohacell 71HF foam plates (ε_foam = 1.10; loss tangent: $16\times {10}^{-4}$; 1.06-mm thickness) and Wuxichaoying K-21 microwave dielectric ceramic plates (ε_ceramic = 21; loss tangent: $1\times {10}^{-4}$; 1-mm thickness). From the effective medium theory, the effective permittivities of the corner cloaks can be obtained as ${\epsilon }_1\hspace{0.17em}=r{\epsilon }_{ceramic}+\left(1-r\right){\epsilon }_{foam}\hspace{0.17em}\text{And}\hspace{0.17em}{\epsilon }_2\hspace{0.17em}={\epsilon }_{ceramic}{\epsilon }_{foam}/\left[\left(1-r\right){\epsilon }_{ceramic}+r{\epsilon }_{foam}\right]$, with the filling factor r = 0.485.

The x–y projection in Fig. S2A shows a feasible transformation of the original electromagnetic space for electromagnetic surface waves propagating on a metal–dielectric interface: the region M_nO_nA_n (Fig. S2A, blue) is transformed into M_nO_nA′_n (Fig. S2A, red), with its area being preserved; symmetrically, the region W_nO_nV_n is transformed into W_nO_nV′_n. The subscript n = 1 or 2 represents the nth 90° corner. Note that, because the surface electromagnetic waves have magnetic fields along the z direction, only the z component of permeability is relevant, which according to the principle of transformation optics, is equal to ${\mu }_z=1/\det \left(\overline{\overline{J}}\right)$, where $\det \left(\overline{\overline{J}}\right)$ is the Jacobian of the transformation. Because the Jacobian represents the change of an infinitesimal area in the transformation, the area preservation from M_nO_nA_n to M_nO_nA′_n and from W_nO_nV_n to W_nO_nV′_n guarantees that ${\mu }_z=1$. Thus, we can implement a perfect full-parameter metamaterial corner cloak with dielectric materials. For |A_nO_n| = 50 mm, |A_nM_n| = 75 mm, and |A′_nO_n| = 42.4 mm, the required principal permittivities of the corner cloaks are ε₁ = 10.7 and ε₂ = 2.0. Fig. S2B shows triangular pieces of the metamaterial structure. Four identical triangles of the metamaterial structure form two corner cloaks that effectively bend surface waves across the two right-angle zero-radius corners of the U-shaped waveguide.

Specifications of the Carpet Cloak.

Fig. S3A illustrates the 3D scheme of the carpet cloak and the grooved surface-wave waveguide with a sharp bump. The carpet cloak is constructed with a layered metamaterial structure composed of Wuxichaoying K-21 microwave dielectric ceramic plates (ε_ceramic = 21; loss tangent: $\hspace{0.17em}1\times {10}^{-4}$; 1-mm thickness) and Rohacell 71HF foam plates (ε_foam = 1.10; loss tangent: $\hspace{0.17em}16\times {10}^{-4}$; 1.06-mm thickness).

The x–y projection in Fig. S3A shows the area-preserving transformation for the carpet cloak. The original rectangular space HIJK (Fig. S3A, blue) is transformed into two symmetric and connected parallelograms HMNK and IMNJ (Fig. S3A, red) under the area preservation constraint. The constitutive parameters of the transformation medium are obtained with the same method used for the corner cloaks. Because the area is invariant in the transformation, the permeability is intrinsically unitary. For |HI| = 100 mm, |HM| = 66.6 mm, and |HK| = 50 mm, the carpet cloak requires the same metamaterial used for the corner cloaks. Fig. S3B shows details of the ceramic/foam-layered metamaterial structure.