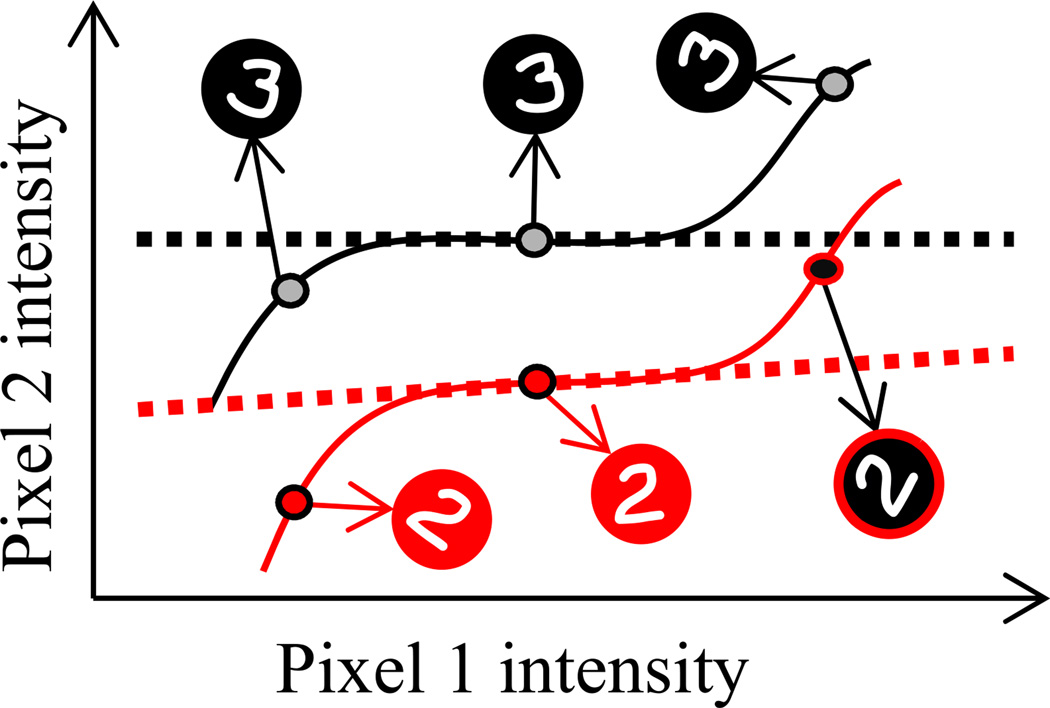
Figure 5. Suboptimal Inference on Inputs without Internal Noise.

Handwritten digit recognition can be formalized as a problem of modeling manifolds in n-dimensional space, where n is the number of pixels in the image. Each point in this space corresponds to one particular image (only two dimensions are shown for clarity). We show here a schematic representation of the manifolds corresponding to rotated 2s (red solid line) and 3s (black solid line). Modeling these manifolds is typically hard and requires approximations. One common approach involves using a locally linear approximation, shown here as dashed lines. This approximation would result in misclassifying the image of the 2 shown with a black background as a 3, as it lies closer to the linear approximation of the manifold corresponding to 3. This illustrates how suboptimal inference can affect behavioral performance even when the inputs are unaffected by internal noise.