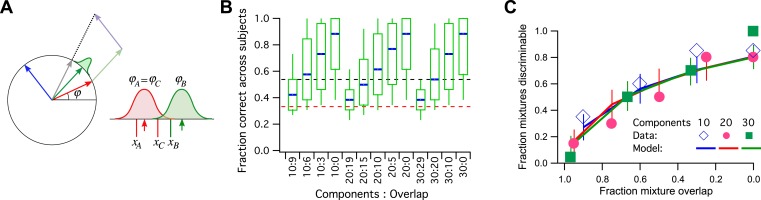
Figure 3. A model simulation of the human smell experiments.
(A) Left: Each primary odor gets mapped into a unit vector (e.g., red, green, blue). Mixtures of odors get mapped into the normalized sum vector (gray). Right: When a subject sniffs an odor vial, the odor angle is corrupted by Gaussian noise and a value is drawn from that distribution. Here three vials were presented, two (A and C) containing the identical odor and a third (B) a different odor. This produced response variables xA, xB, and xC. On this trial, xB and xC are closest to each other, so the subject (incorrectly) identifies A as the odd odor. (B) Discriminability of odor mixtures under this model (compare to Bushdid et al., 2014, Figure 2C). Mixtures were simulated according to the reported procedure with 10, 20, or 30 components and varying overlap. Each mixture pair was presented to 26 subjects, and the fraction of correct identification determined across subjects. Box-and-whisker plot shows the distribution of that fraction with percentiles 10, 25, 50, 75, 90. Average over 1000 repeats of the procedure with different random numbers. Red dashes: chance performance. Black dashes: criterion for discriminability (14/26 correct). (C) Fraction of discriminable mixtures as a function of their overlap (compare to Bushdid et al., 2014, Figure 3D). This is the fraction of mixture pairs in each class that exceeds 50% correct identification across subjects (above the black line in panel B). Lines are mean ± SD. Symbols are data from Bushdid et al. (2014). The model used Gaussian noise with a SD of 0.4 radians.