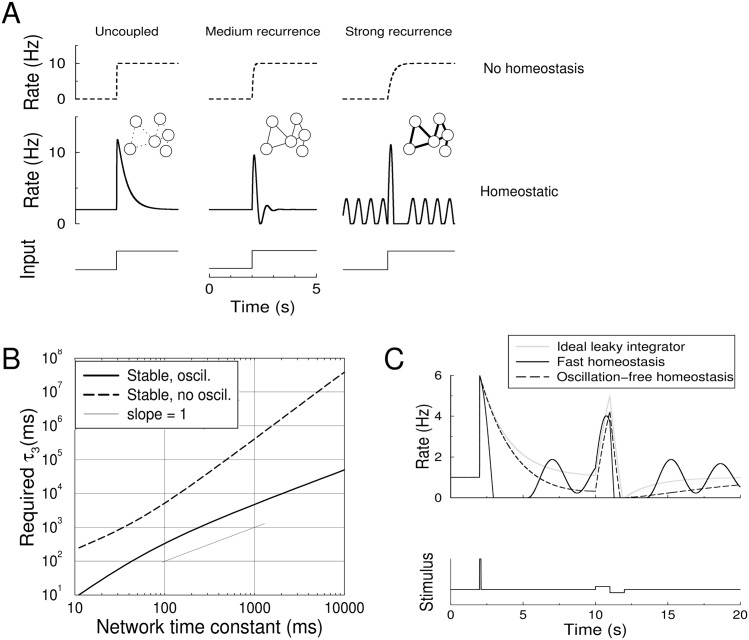
Fig 2. Homeostasis can destabilize activity in otherwise stable networks.

A) Activity in a homeostatic network with varying levels of recurrence, but identical homeostatic parameters (τ ₁ = 10ms, τ ₂ = 50ms, τ ₃ = 500ms). Without homeostasis even the strongly recurrent network is stable (top row). With homeostasis, although the network in stable in the absence of synaptic coupling (left), with increasing recurrence the network shows increasing oscillatory activity (middle, w _m = 0.8), and becomes unstable for strong recurrence, leading to unabating oscillations (right, w _m = 0.95). B) The requirements on the homeostatic time-constant as a function of the recurrence of the network, expressed in terms of the network time-constant, which equals τ ₁/(1 − w _m). Shown are the minimal value of τ ₃ to ensure stability, potentially with damped oscillations (solid curve) and the minimal value of τ ₃ for a stable firing rate without oscillation (dashed curve). C) The interference of homeostatic control with a neural integrator. The response of an ideal leaky-integrator with 1s time-constant (gray curve) to a pulse at 2s, and a bi-phasic pulse at 10 s. The response of a stable, but oscillatory homeostatic network is very different from the non-homeostatic case (black curve, τ ₃ = 7s). Only when the homeostasis is slow enough to be oscillation-free, the response approximates that of the ideal integrator (dashed curve, τ ₃ = 420s).