Fig. 5.

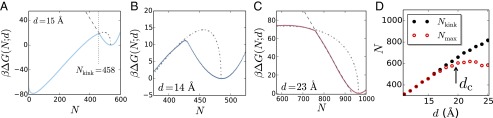
(A) The simulated $\beta \mathrm{\Delta }G\left(N;d\right)$ for $d=15\hspace{0.17em}\AA$ (solid) is shown along with the expected metastable branches of the free energies corresponding to the vapor tube (dot-dashed) and isolated cavity (dashed) ensembles. The metastable branches are anticipated from the fits shown in Fig. 4. The system minimizes its free energy by localizing to the ensemble with the lower free energy. (B) For $d=14$ Å, the nascent vapor tube formed at the kink is larger than the critical vapor tube anticipated by macroscopic theory, and therefore grows spontaneously. As a result, the corresponding barrier to dewetting is smaller than that predicted by macroscopic theory. (C) For larger separations, here $d=23$ Å, the newly formed vapor tube is subcritical, and has to grow larger for dewetting to proceed. (D) Comparison of the location of the kink, $N_{\text{kink}}$, with the location of the barrier between the liquid and vapor basins, $N_{\text{max}}$. For small d, the barrier (point of highest $\mathrm{\Delta }G$) occurs at the kink, so that $N_{\text{max}}\approx N_{\text{kink}}$. In contrast, for larger d values, the barrier occurs in the vapor tube segment of the simulated free energy profile and corresponds to the classical critical vapor tube, so that $N_{\text{max}}<N_{\text{kink}}$. The transition from nonclassical to classical behavior occurs in the vicinity of the coexistence separation, $d_{\text{c}}$.