ADJUSTING FOR BIAS DUE TO INCOMPLETE CASE ASCERTAINMENT IN CASE-CONTROL STUDIES OF BIRTH DEFECTS

Abstract

Case-control studies of birth defects might be subject to selection bias when there is incomplete ascertainment of cases among pregnancies terminated following prenatal diagnosis of the defect. We propose a simple method to estimate inverse probability of selection weights (IPSWs) for cases ascertained from pregnancies both ending and not ending in termination using data directly available from the National Birth Defects Prevention Study and other published information. The IPSWs can then be used to adjust for selection bias analytically. We can also allow for uncertainty in the selection probabilities through probabilistic bias analysis. We provide an illustrative example using data from National Birth Defects Prevention Study (1997–2009) to examine the association between prepregnancy obesity (body mass index ≥30 vs. <30 kg/m²) and spina bifida. The unadjusted odds ratio (OR) for prepregnancy obesity and spina bifida is 1.48 (95% confidence interval: 1.26, 1.73), and the simple selection bias-adjusted OR is 1.26 (95% confidence interval: 1.04, 1.53). The probabilistic bias analysis resulted in a median adjusted OR of 1.22 (95% simulation interval: 0.97, 1.47). The proposed method provides a quantitative estimate of the IPSWs and the bias introduced by incomplete ascertainment of cases among terminated pregnancies conditional on a set of assumptions.

INTRODUCTION

Selection bias is a concern in birth defect studies. Several potential mechanisms have been posited (1–4), including bias due to incomplete ascertainment of cases among terminated pregnancies (5–13). Because ascertainment of terminated pregnancies is more difficult than ascertainment of live births and stillbirths, selection bias can occur when prenatal diagnosis of a birth defect increases the probability of termination, and termination differs by exposure status (6, 9). For example, some birth defects might be more difficult to visualize by prenatal ultrasound with increasing body mass index (BMI) (14, 15). Therefore, obese women could be less likely to receive a prenatal diagnosis and consequently, less likely to consider terminating an affected pregnancy. Thus, in a study of prepregnancy obesity and birth defects, both the exposure and the outcome could affect selection, potentially resulting in selection bias. Generally, the extent of case under-ascertainment in birth defects studies is unknown and likely varies widely by setting and ascertainment method (13, 16–18).

Although prior papers propose formulas to address incomplete case ascertainment in birth defect studies (5, 6), we were unable to find studies implementing these approaches. This is likely due to the challenge of identifying sufficient information to estimate the required exposure-specific selection probabilities (19). We propose a method to estimate inverse probability of selection weights (IPSWs) to adjust for selection bias arising from incomplete ascertainment of cases. We estimate IPSWs and bias-adjusted odds ratios (OR) using data from the National Birth Defects Prevention Study (NBDPS).

MOTIVATING EXAMPLE

Epidemiologic studies have consistently found associations between prepregnancy obesity and spina bifida (11, 20). However, it has been posited that these associations might be explained by selection bias from incomplete ascertainment of cases among pregnancies ending in termination (10–12).

We illustrate the disposition of fetuses with spina bifida in Figure 1 where a fetus can receive prenatal testing or not, and if tested, spina bifida can be diagnosed or not. Each pregnancy could end in spontaneous abortion, termination, live birth, or stillbirth. In most birth defects studies, spontaneous abortions are excluded because they are difficult to identify, particularly at early gestational ages, and the presence or absence of a birth defect is often unknown. For this reason, we exclude them from our analysis. Prenatal diagnosis of a birth defect can lead to termination of a pregnancy, or termination can occur for reasons unrelated to prenatal diagnosis (among untested pregnancies and those with a false negative result). Our approach allows for incomplete ascertainment of both types of terminations. We exclude pregnancies terminated prior to 13 weeks, approximately the earliest gestational age at which spina bifida could be prenatally diagnosed (21), because most epidemiologic studies do not ascertain these cases. We assume terminated pregnancies at 13 gestational weeks and older are incompletely ascertained. For simplicity, we assume complete ascertainment of pregnancies ending in live birth or stillbirth. Our approach could address incomplete ascertainment of liveborn and stillborn cases, but for spina bifida, case ascertainment of live births and stillbirths is thought to be high (22). Thus, for this example, the cases include all live births and stillbirths with spina bifida and a subset of pregnancies affected by spina bifida that were terminated at gestational age 13 weeks or later.

FIGURE 1.

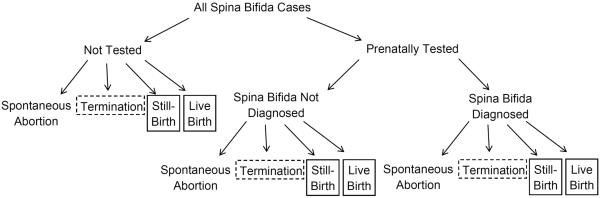
The possible outcomes of all pregnancies in which spina bifida is present are illustrated. The pregnancies receive prenatally testing or not, and if tested, spina bifida is prenatally diagnosed or not. Four outcomes are possible for each pregnancy: spontaneous abortion, termination of pregnancy, live birth, or stillbirth. We assume complete ascertainment of live and stillbirths (boxes with solid outline); incomplete ascertainment of terminations at or after 13 weeks gestation and no ascertainment of terminations prior to 13 weeks gestation (boxes with dashed outline); and no ascertainment of spontaneous abortions.

Although under ascertainment of cases can occur in a cohort study or a case-control study, for birth defect studies, the case-control design is more feasible (and more common) because birth defects are relatively rare outcomes (17). For our example, controls are a random sample of live births with no major birth defects, consistent with the design of many birth defect studies (23–25).

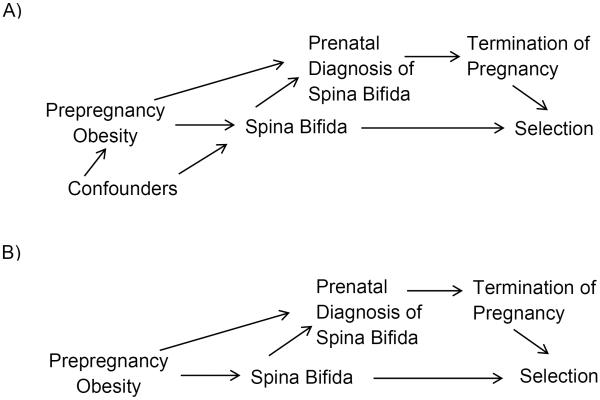
In the directed acyclic graph (DAG) in Figure 2A, we hypothesize that prepregnancy obesity affects spina bifida, having spina bifida affects whether or not spina bifida is prenatally diagnosed, and prenatal diagnosis affects whether a pregnancy is terminated or not. Further, prepregnancy obesity affects whether or not a fetus is prenatally diagnosed by impairing ultrasound visualization of spina bifida. In a case-control study, the outcome affects selection into the study. Pregnancy termination also affects selection into the study because of incomplete ascertainment of terminated pregnancies. The effect of prepregnancy obesity on spina bifida might be confounded by unspecified confounders (Figure 2A). In prior studies, results adjusted for suspected confounders have differed minimally from unadjusted results (11, 12) although unidentified confounders may still exist. For clarity, we start with an overly simplistic DAG in which we assume no unmeasured confounders (Figure 2B). Then we adjust for selection bias in the presence of suspected confounding. For both scenarios, we assume the exposure, outcome, and prenatal diagnosis are not misclassified or missing.

FIGURE 2.

A: In this directed acyclic graph (DAG), we are interested in the effect of prepregnancy obesity on spina bifida in pregnancies surviving to 13 weeks gestation. There might be confounders of this association (e.g., race/ethnicity). Having spina bifida affects the likelihood of prenatal diagnosis, and prepregnancy obesity affects whether spina bifida is diagnosed prenatally. Having a prenatal diagnosis of spina bifida affects the likelihood of termination of pregnancy. In a case-control study, spina bifida affects selection into the study. Termination also affects selection because terminated pregnancies are more difficult to ascertain. B: Is a simplified version of DAG A. In DAG B, we assume there are no unmeasured confounders.

APPROACH

Our goal is to estimate the association between prepregnancy obesity and spina bifida adjusted for bias due to incomplete ascertainment of cases. We do this by estimating IPSWs, which we use to calculate a bias-adjusted association in a pseudopopulation with complete case ascertainment (26). Essentially, each case is weighted by the inverse of the probability that a case with those characteristics is selected. For example, because terminated cases are less likely to be selected than cases that are not terminated, selected terminated cases are weighted heavier than selected liveborn and stillborn cases to compensate for the missing cases. This recreates the distribution of the cases in the source population assuming that the selected cases are representative of the unobserved cases.

To estimate IPSW, first we need to estimate selection probabilities for cases among terminated pregnancies conditional on obesity status of the woman and prenatal diagnosis status of the fetus: P(S|T,Ob,Dx), $\mathrm{P}(\mathrm{S}\mid \mathrm{T},\overline{Ob},\mathrm{Dx})$,$\mathrm{P}(\mathrm{S}\mid \mathrm{T},\mathrm{Ob},\overline{Dx})$, and $\mathrm{P}(\mathrm{S}\mid \mathrm{T},\overline{Ob},\overline{Dx})$, where S represents selection (S: selected, $\overline{\mathrm{s}}:\text{not selected}$), T represents termination of pregnancy (T: terminated, $\overline{\mathrm{T}}:\text{not terminated}$), Ob represents prepregnancy obesity (Ob: obese, $\overline{Ob}:\text{not obese}$), and Dx represents prenatal diagnosis with spina bifida (Dx: diagnosed, $\overline{Dx}:\text{not diagnosed}$). In Figure 2B, selection of cases is independent of prepregnancy obesity and prenatal diagnosis given termination because among cases, prepregnancy obesity only affects selection of terminated pregnancies through prenatal diagnosis, and prenatal diagnosis only affects selection through termination. Thus, the four selection probabilities can be simplified to the common probability P(S|T). Similarly, selection of cases is independent of prepregnancy obesity and prenatal diagnosis given no termination of pregnancy and can be simplified to $\mathrm{P}(\mathrm{S}\mid \overline{T})$. Thus, given our assumptions, we need only 2 IPSW, which are conditional on whether the pregnancy was terminated or not and which can be calculated as follows.

First, we assume that the likelihood of pregnancy termination for cases is independent of prepregnancy obesity given prenatal diagnosis (Figure 2B):

$$\mathrm{P}(\mathrm{T}\mid \mathrm{Dx},\mathrm{Ob})=\mathrm{P}(\mathrm{T}\mid \mathrm{Dx},\overline{\mathrm{Ob}})=\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})$$

$$\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}},\mathrm{Ob})=\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}},\overline{\mathrm{Ob}})=\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})$$

Given our assumptions, we can estimate P(Dx|Ob) using Equation 1:

$$\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})=\frac{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right][1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\right]+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}$$

A detailed proof is provided in Appendix 1. Similarly, $\mathrm{P}(\mathrm{Dx}\mid \overline{Ob})$ can be estimated using Equation 2:

$$\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})=\frac{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\overline{\mathrm{Ob}},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right][1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\overline{\mathrm{Ob}},\mathrm{S}\left)\right]+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\overline{\mathrm{Ob}},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}$$

Only 3 probability estimates are needed for each equation: 1) the probability of prenatal diagnosis among pregnancies in the study that were not terminated conditional on prepregnancy obesity status $\left(\mathrm{P}\right(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\mathrm{or}\mathrm{P}\right(\mathrm{Dx}\mid \overline{T},\overline{Ob},\mathrm{S}\left)\right)$, 2) the probability of termination given prenatal diagnosis (P(T|Dx)), and 3) the probability of termination given no prenatal diagnosis $\left(\mathrm{P}\right(\mathrm{T}\mid \overline{Dx}\left)\right)$. These probabilities can be estimated from study data, if available, or the literature.

The next step is to use these values to estimate P(S|T) using Equation 3:

$$\mathrm{P}(\mathrm{S}\mid \mathrm{T})=\frac{\frac{{\mathrm{M}}_1}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})}+\frac{{\mathrm{M}}_2}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})}}{\frac{{\mathrm{Q}}_1}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}+\frac{{\mathrm{Q}}_2}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}}$$

where M₁ is the number of obese cases selected into the study with T and Dx, M₂ is the number of non-obese cases selected into the study with T and Dx, Q₁ is the number of obese cases selected into the study with $\overline{T}$, and Q₂ is the number of non-obese cases selected into the study with $\overline{T}$. These values can be determined directly from study data if available. The proof of this equation is provided in Appendix 2.

The estimated IPSW for cases among terminated pregnancies is w_T=1/P(S|T). The estimated IPSW for liveborn and stillborn cases is ${\mathrm{w}}_{\overline{\mathrm{T}}}=1∕\mathrm{P}(\mathrm{S}\mid \overline{T})$, which can be estimated from the literature or from study participation rates. Under our assumption of complete ascertainment of live births and stillbirths, $\mathrm{P}(\mathrm{S}\mid \overline{T})=1$.

The IPSW can be use to adjust for selection bias by hand or using modeling software (26). Each case ascertained among terminated pregnancies is assigned IPSW=1/P(S|T), and each liveborn or stillborn case is assigned the $\text{IPSW}=1∕\mathrm{P}(\mathrm{S}\mid \overline{T})$, which equals 1 in this example. All controls are assigned IPSW=1 under the assumption that the distribution of prepregnancy obesity in the controls represents the distribution in the source population. To estimate standard errors and confidence intervals, a robust variance estimator must be used to take into account the inflation of sample size introduced by weighting; for example, in SAS Version 9.3 (SAS Institute, Cary, NC), PROC GENMOD could be used with the REPEATED statement (Web Appendix 1). In the presence of confounding, separate IPSWs for each stratum of the confounder are required. These confounder-specific weights are applied in a model that includes the confounder as an independent variable.

An Excel worksheet that calculates the IPSWs, the bias-adjusted contingency table, and the bias-adjusted OR is available from the corresponding author upon request. The calculated IPSWs can then be applied in a statistical software program such as SAS to obtain the bias-adjusted 95% confidence interval.

We can allow for uncertainty in the estimates used to calculate the IPSW (e.g., P(T|Dx)) by performing a probabilistic bias analysis (19). First, each of the parameters is assigned a probability distribution reflecting the uncertainty about its true value. Then, we repeatedly sample from each distribution and calculate the corresponding IPSWs, which are used to estimate the bias-adjusted OR. The median bias-adjusted OR across all samples provides a point estimate. To calculate a 95% simulation interval (SI) the following formula must be applied to each bias-adjusted OR: exp(log(bias-adjustedOR_i)+error_i) where i=1 to the total number of samples, and error_i is drawn from ~N(0,s), where s is the standard deviation of the unadjusted OR. The resulting 2.5^th and 97.5^th percentiles define the 95% simulation interval.

NUMERIC EXAMPLE

We illustrate this approach using data from NBDPS, a large, multi-site, population-based case-control study of risk factors for major structural birth defects. NBDPS has been described in detail elsewhere (23). In brief, cases with one or more major birth defects were identified through surveillance programs, and controls (liveborn infants with no major birth defect) were identified from birth certificate or hospital records from the same catchment areas and time period as the cases. Study participants were recruited from women giving birth on or after October 1, 1997 with an estimated date of delivery through December 31, 2009. This analysis is limited to NBDPS sites that ascertain cases among live births, stillbirths (fetal deaths ≥ 20 weeks gestation), and terminated pregnancies (functionally limited to gestational ages when a prenatal diagnosis is possible): Arkansas, California, Georgia, Iowa, New York (2000–2009), North Carolina (2003–2009), Texas, and Utah (2003–2009). Procedures for ascertaining cases among terminated pregnancies vary by study site. Ascertainment is likely incomplete at all sites although the extent of under-ascertainment varies. For simplicity, we estimate average IPSWs across sites. NBDPS was approved by institutional review boards at all participating sites.

Participating women completed a computer-assisted telephone interview 6 weeks to 2 years after the estimated date of delivery. BMI was calculated using self-reported prepregnancy weight (kilograms) divided by self-reported height squared (meters). For simplicity, in this example, study participants are classified as obese (BMI ≥30) or not obese (BMI < 30). Women with missing BMI (cases: n=72 (7%); controls: n=434 (5%)) or unknown pregnancy outcome (4 cases; 31 controls) are excluded from this analysis. The final sample includes 929 women with pregnancies affected by spina bifida (cases) and 7,774 women with unaffected pregnancies (controls).

Prenatal diagnosis of spina bifida

Information on prenatal diagnosis of spina bifida was collected during the interview for women with estimated delivery dates through December 31, 2005. After this time, the interview did not include questions about prenatal diagnosis. Women were asked if they had an abnormal ultrasound and if yes to describe the abnormality. We classified women as reporting a prenatal diagnosis if they identified spina bifida by name, provided an anatomical description consistent with spina bifida, described an anomaly that was likely to be spina bifida, or reported fetal surgery for in utero spina bifida repair. Classification of prenatal diagnosis was made by two reviewers who successfully resolved all differences by consensus. Classification was done with knowledge of case status to decrease false negatives due to vaguely reported ultrasound results. Women who reported diagnoses based on amniocentesis, chorionic villus sampling, serum alpha-fetoprotein screening, or other prenatal tests were classified as reporting a prenatal diagnosis even though these tests are not diagnostic for spina bifida. We assumed that these women did not remember that the ultrasound provided the confirmatory diagnosis.

Estimation of IPSWs

The IPSWs for the cases are estimated from data collected by NBDPS and data available in the literature (Table 1). The following information for both obese women and women who are not obese are available directly from NBDPS: 1) the number of women with pregnancies prenatally diagnosed with spina bifida that were terminated, 2) the number of women whose pregnancies were not terminated, and 3) the proportion of women in the study with a liveborn or stillborn case reporting a prenatal diagnosis. These data are assumed to apply to the full study period but are restricted to women with an estimated delivery date of December 31^st, 2005 or earlier because only these women in NBDPS were asked about prenatal diagnosis. The fact that prenatal diagnosis of other birth defects did not increase from 2000–2005 provides some support for this assumption (27, 28).

TABLE 1.

Description, Notation, Value, and Source of Counts and Percents Needed to Calculate Weights to Adjust for Selection Bias Due to Incomplete Ascertainment of Cases Among Pregnancies Terminated Following Prenatal Diagnosis.^a

Description	Notation	Value	Source
Number of obese women in the study with pregnancies that were prenatally diagnosed and terminated	M1	8	Directly observed countb
Number of not obese women in the study with pregnancies that were prenatally diagnosed and terminated	M2	46	Directly observed countb
Number of obese women in the study with pregnancies that were not terminated	Q1	142	Directly observed countb
Number of not obese women in study with pregnancies that were not terminated	Q2	372	Directly observed countb
Among obese women in the study with pregnancies that were not terminated, the proportion with a prenatal diagnosis	$\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})$	0.55	Calculate based on directly observed countsb
Among not obese women in the study with pregnancies that were not terminated, the proportion with a prenatal diagnosis	$\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\overline{\mathrm{Ob}},\mathrm{S})$	0.50	Calculate based on directly observed countsb
Among all pregnancies affected by spina bifida that were prenatally diagnosed, the proportion that were terminated	P(T|Dx)	0.49	Need estimate from literature
Among all pregnancies affected by spina bifida that were not prenatally diagnosed, the proportion that were terminated	$\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})$	0.03	Need estimate from literature
Among pregnancies affected by spina bifida that are not terminated, the proportion that are selected	$\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})$	1.00	Based on study design
Among obese women with pregnancies affected by spina bifida, the proportion of pregnancies that are prenatally diagnosed	P(Dx|Ob)	0.70	Estimated using Equation 1
Among not obese women with pregnancies affected by spina bifida, the proportion of pregnancies that are prenatally diagnosed	$\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})$	0.66	Estimated using Equation 2
Among all pregnancies affected by spina bifida and terminated, the proportion that are selected	P(S|T)	0.21	Estimated from above using Equation 3
Weight applied to terminated case pregnancies in the study	wT	4.65	1/P(S|T)
Weight applied to live birth and stillbirth cases in the study	$w_{\overline{\mathrm{T}}}$	1.00	$1∕\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})$

^aAll Data in the Table Are Restricted to Pregnancies Affected by Spina Bifida Only.

^bBased on study population with an estimated delivery date on or before December 31^st, 2005, which restricts the population to women who were asked about prenatal testing. We assume the proportions do not change over time.

The proportion of terminated pregnancies among all prenatally diagnosed pregnancies affected with spina bifida is estimated from a recent systematic review (16). The proportion of pregnancies terminated at gestational age 13 weeks or later among pregnancies affected with spina bifida but not prenatally diagnosed is also estimated from the literature. This value is less readily available; the derivation of our estimate is described in the Web Appendix 2 (29, 30). We assume that NBDPS has complete ascertainment of liveborn and stillborn spina bifida cases in the states included for this study so $\mathrm{P}(\mathrm{S}\mid \overline{T})=1.00$ and thus IPSW=1.

Inserting the values from Table 1 into Equations 1 and 2, we estimate the proportion of pregnancies affected by spina bifida that were prenatally diagnosed among obese and not obese women. Next, we use Equation 3 to estimate the proportion of pregnancies selected into the study among terminated, affected pregnancies. The IPSW for terminated cases is the inverse of this proportion.

Adjustment for selection bias

The unadjusted and bias-adjusted contingency tables are presented in Table 2. Prior to adjusting for incomplete ascertainment of cases among pregnancies that were terminated, the OR for prepregnancy obesity (obese vs. not obese) and spina bifida is 1.48 (95% confidence interval (CI): 1.26, 1.73) (Table 3). The adjusted number of cases is calculated by applying w_T to terminated cases in the study and ${\mathrm{w}}_{\overline{\mathrm{T}}}$ to liveborn and stillborn cases within strata of obese and not obese women. The OR adjusted for selection bias is 1.26 (95% CI: 1.04, 1.53), given our assumptions.

TABLE 2.

Observed and Bias-Adjusted Contingency Tables for Prepregnancy Obesity (Exposure) and Spina Bifida (Outcome), Selected National Birth Defects Prevention Study Sites, 1997–2009.

	Observed		Bias-Adjusteda
	Obese	Not Obese	Obese	Not Obese
Case	239	690	290.2	978.7
Control	1477	6297	1477.0	6297.0

^aAdjusted for selection bias due to incomplete ascertainment of cases among pregnancies terminated following prenatal diagnosis with spina bifida.

TABLE 3.

Unadjusted and Selection Bias-Adjusted Associations Between Prepregnancy Obesity (Obese vs. Not Obese) and Spina Bifida, Selected National Birth Defects Prevention Study Sites, 1997–2009.

	Model 1a				Model 2a				Model 3a
Analysis	OR	(95% CI)	Median ORb	(95% SI)c	OR	(95% CI)	Median ORb	(95% SI)c	OR	(95% CI)	Median ORd	(95% SI)c
Uncorrected	1.48	(1.26–1.73)			1.49	(1.27–1.75)			1.49	(1.27–1.75)
Simple selection bias correctione	1.26	(1.04–1.53)			1.28	(1.06–1.56)			1.34	(1.11–1.62)
Probabilistic selection bias correction			1.22	(0.97–1.47)			1.22	(1.01–1.46)			1.29	(1.07–1.53)

Abbreviations: CI, confidence interval; OR, odds ratio; SI, simulation interval

^aModel 1: unadjusted for race/ethnicity (Figure 2B); Model 2: adjusted for race/ethnicity assuming Figure 2A is correct (race/ethnicity as a confounder); Model 3: adjusted for race/ethnicity assuming Figure 3 is correct (race/ethnicity as the sociocultural factor)

^bProbabilistic weight applied to terminated cases using formulae from Table 1 and a triangular distribution (minimum, mode, maximum) of (0.36, 0.49, 0.82) for the proportion of all prenatally diagnosed cases that are terminated and (0.00, 0.03, 0.06) for the proportion of all cases that were not prenatally diagnosed and terminated; weight of 1.00 applied to live born and stillborn cases; weight of 1.00 applied to controls

^c2.5th to 97.5th percentiles of the corrected OR after incorporating random error sampled from a normal distribution with a mean of 0 and a standard deviation equal to the standard error for the uncorrected OR (Unadjusted: 0.0804; Adjusted Figures 2A and 3: 0.0808)

^dProbabilistic weight applied to terminated cases using formulae from Table 1 and a triangular distribution (minimum, mode, maximum) for the proportion of prenatally diagnosed cases that are terminated of (0.38, 0.51, 0.84) for white, (0.22, 0.35, 0.68) for black, (0.18, 0.31, 0.64) for Hispanic, and (0.37, 0.50, 0.83) for other and a triangular distribution for the proportion of all cases that were not prenatally diagnosed and terminated of (0.00, 0.01, 0.04) for white, (0.03, 0.06, 0.09) for black, (0.00, 0.02, 0.05) for Hispanic, and (0.00, 0.03, 0.06) for other; weight of 1.00 applied to live born and stillborn cases; weight of 1.00 applied to controls

^eWeight of 3.86 applied to terminated cases; weight of 1.00 applied to live born and stillborn cases; weight of 1:00 applied to controls

To allow for uncertainty in the estimates of P(T|Dx) and $\mathrm{P}(\mathrm{T}\mid \overline{Dx})$, we performed a probabilistic bias analysis. We assigned P(T|Dx) a triangular distribution based on the systematic review of pregnancy termination following prenatal diagnosis with spina bifida (16). We chose a triangular distribution because it allows specification of a maximum probability corresponding to the point estimate we hypothesize to be the most likely and decreasing probability of selection on either side of that value. The lower and upper limits of the distribution define the hypothesized minimum and maximum plausible estimates. We fixed the mode of the distribution to equal the overall frequency of termination of pregnancies diagnosed prenatally with spina bifida in the United States (0.49) and set the lower limit of the distribution to be the lowest proportion reported (0.36) and the upper limit to be the highest proportion reported (0.82) for studies in the United States. For $\mathrm{P}(\mathrm{T}\mid \overline{Dx})$ we used a triangular distribution with a mode of 0.03 (Web Appendix 2), a lower limit of 0.00, and an upper limit of 0.06. We performed 10,000 iterations of the bias analysis. Given our assumptions, the median bias-adjusted OR was 1.22 with a 95% simulation interval including random error of 0.97 to 1.47 (Table 3).

Confounding example

To illustrate adjusting for selection bias in the presence of confounding, we assume race/ethnicity is a confounder (Figure 2A) and recreate table 1 for each stratum of race/ethnicity (Web Table 1). The first 6 rows are available from NBDPS, and P(T|Dx), $\mathrm{P}(\mathrm{T}\mid \overline{Dx})$, and $\mathrm{P}(\mathrm{S}\mid \overline{T})$ are unchanged because they are not affected by race/ethnicity. Race/ethnicity-specific weights are calculated based on the new values and applied in models adjusting for race/ethnicity. The results are similar to those assuming no confounding (Table 3).

For simplicity, we assumed that prepregnancy obesity is only associated with pregnancy termination through prenatal diagnosis. However, this may be incorrect. For example, a sociocultural factor could affect both prepregnancy obesity and termination of pregnancy through a path that does not include prenatal diagnosis (Figure 3). In fact, the prevalence of prepregnancy obesity varies by race/ethnicity (31) as does the probability of terminating a pregnancy after a prenatal diagnosis (9, 32, 33). Thus, race/ethnicity might represent the sociocultural factor (instead of being a confounder). If Figure 3 is correct, race/ethnicity-specific weights must be calculated using data from NBDPS and race/ethnicity-specific values of P(T|Dx) and $\mathrm{P}(\mathrm{T}\mid \overline{Dx})$ abstracted from the literature (Web Table 2). The results adjusted for selection bias based on Figure 3 are closer to the unadjusted OR than previous scenarios although still closer to the null than the unadjusted results (Table 3).

FIGURE 3.

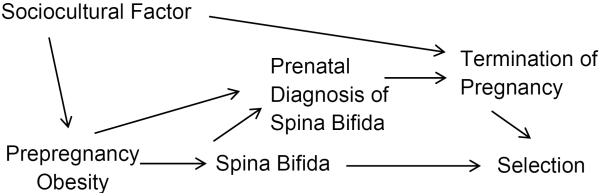
This directed acyclic graph (DAG) expands the DAG in Figure 2B to include an unmeasured sociocultural factor (e.g., race/ethnicity) that affects prepregnancy obesity and the likelihood of termination of pregnancy

DISCUSSION

In this paper, we illustrate a simple method to account for selection bias due to incomplete ascertainment of birth defect cases among pregnancies that are terminated, and we further adapted this method into a probabilistic bias analysis to incorporate uncertainty about the estimates used to calculate the IPSWs. In addition, we illustrate the application of this method in the presence of confounding and in a more complex scenario where the exposure is associated with termination of pregnancy through a path that does not involve prenatal diagnosis.

All bias-adjusted estimates for prepregnancy obesity and spina bifida are closer to the null than the unadjusted OR, which is consistent with our initial hypothesis about the likely direction of bias (up and away from the null). We suspected that obese women with pregnancies affected by spina bifida were overrepresented in the study compared with women who were not obese because fetuses of obese women were less likely to be diagnosed prenatally, and therefore, the pregnancy was less likely to be terminated. In our analyses, however, our calculated probability of prenatal diagnosis was greater in obese women than in women who were not obese (e.g., 0.70 vs. 0.66 in Table 1). This result highlights the value of quantitatively evaluating bias in epidemiologic studies because our intuitions may lead us astray (19).

If, as our estimates suggest, fetuses of obese women are more likely to be diagnosed prenatally than fetuses of women who are not obese, then our DAG (Figure 2B) might be correct, but our hypothesized mechanism (that spina bifida is more difficult to visualize on the ultrasound among obese women) might be incorrect. Alternatively, spina bifida could be more difficult to visualize by ultrasound in obese women, but obese women could be more likely to receive prenatal testing because of the suspicion that they are at higher risk of having an affected pregnancy. In fact, a study examining obesity and detection of fetal anomalies reported that anomalies were less likely to be detected as BMI increased for routine ultrasounds, but this difference was attenuated for ultrasounds performed for high risk pregnancies (14). The relatively small difference between the probabilities could also be due to chance in which case there should not be an arrow between prepregnancy obesity and prenatal diagnosis in the DAG. There may be other possible mechanisms that would be consistent with the estimated probabilities of prenatal diagnosis among obese and not obese women.

As with any bias analysis, the validity of our results is conditional on our assumptions being correct. Although we cannot verify our assumptions, they are informed by the current evidence available in the literature and can easily be varied to assess the range of possible bias given different plausible scenarios. However, our example does not take into account other sources of bias such as misclassification, other types of selection bias, and bias due to missing data. These other sources of bias could be addressed through multiple bias analysis (19).

While our method focuses on selection bias among the cases, a similar approach could be used to evaluate bias that might arise from incomplete selection of controls among terminated pregnancies. However, many studies, such as NBDPS, only select controls from live births so P(S|T)=0 and therefore, the IPSW would be undefined. Nevertheless, if the distribution of prepregnancy obesity in control women is representative of the distribution of prepregnancy obesity in the source population, any bias would likely be minimal.

Although adjustment for bias is often done to obtain a more valid estimate of a causal effect, the association we investigated does not have a straightforward causal interpretation due to practical limitations of birth defect studies. A detailed discussion of methodologic issues in conducting etiologic studies of birth defects is beyond the scope of this paper, but we briefly highlight some issues of concern. The research question we would like to answer is whether or not prepregnancy obesity causes spina bifida. Ideally, this question would be addressed among all conceptions including spontaneous abortions. However, including spontaneous abortions is rarely possible because they are often unrecognized and even among recognized losses, it is difficult to identify birth defects. Bias can occur when spontaneous abortions are excluded but both the exposure and the outcome affect the probability of pregnancy loss (1). Even a causal interpretation of the association between prepregnancy obesity and spina bifida conditional on surviving to 13 weeks gestation may be questionable if prepregnancy obesity affects pregnancies that terminate prior to 13 weeks (34). Further, any causal interpretation of our results is limited by the fact that being obese might not be exchangeable with not being obese (35). Thus, even bias-adjusted results should be interpreted with caution.

Exclusion or incomplete ascertainment of birth defects cases among terminated pregnancies poses a continuing challenge to birth defects research (36). Studies have found substantial differences in the estimated prevalence of many types of birth defects depending on whether cases among terminated pregnancies are included or not and depending on the source used to ascertain these cases (e.g., hospitals vs. prenatal clinics) (13, 17, 18). Even with multiple sources of ascertainment, birth defects surveillance programs typically cannot achieve complete case ascertainment among terminated pregnancies, and the proportion of cases missed remains unknown but is likely substantial for some defects such as spina bifida.

Our approach allows the potential impact of this mechanism of selection bias to be assessed without requiring knowledge of the proportion of cases missed. In fact, it estimates this probability, P(S|T) under specific assumptions. In this example, the probability of selection among all terminated affected pregnancies was 21%, indicating that NBDPS study sites ascertaining cases among terminated pregnancies might be missing 79% of terminated, affected pregnancies. While our assumptions are unverifiable, this estimate indicates the potential for substantial under-ascertainment given a plausible scenario. In addition to estimating bias-adjusted ORs, our method could be adapted to estimate the completeness of case ascertainment by surveillance systems (which might require estimating some values not collected by the surveillance system, e.g., $\mathrm{P}(\mathrm{Dx}\mid \overline{T},\mathrm{Ob},\mathrm{S})$.

The proposed method for calculating IPSWs allows us to quantitatively estimate the magnitude of bias introduced by incomplete ascertainment of cases among terminated pregnancies, given several assumptions. The method is simple to implement and the information needed to calculate the IPSWs is available from the literature and directly from the study in some cases. Further, the method can be adapted to address more complex scenarios such as situations where confounding is present or the hypothesized DAG is different. Although the proposed bias adjustment does not guarantee an unbiased association, it provides the opportunity to quantitatively explore alternative explanations for the observed unadjusted results and to improve our understanding of the uncertainty in these results due to selection bias. This attention to an important potential source of systematic error can only improve our ability to draw conclusions about a study compared with strictly qualitative attempts to consider the likely role of selection bias.

APPENDIX 1

Below we provide a detailed derivation of Equation 1, which is used to estimate P(Dx|Ob). The estimate of P(Dx|Ob) is derived from the following equation:

$$\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})=\frac{\mathrm{P}(\overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\mid \mathrm{Dx})\mathrm{P}\left(\mathrm{Dx}\right)}{\mathrm{P}(\overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\mid \mathrm{Dx})\mathrm{P}\left(\mathrm{Dx}\right)+\mathrm{P}(\overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\mid \overline{\mathrm{Dx}})\mathrm{P}\left(\overline{\mathrm{Dx}}\right)}$$

We know that

$$\begin{array}{cc}\hfill \mathrm{P}(\overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\mid \mathrm{Dx})& =\mathrm{P}(\mathrm{Ob}\mid \mathrm{Dx})\mathrm{P}(\overline{\mathrm{T}}\mid \mathrm{Ob},\mathrm{Dx})\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{Dx})\hfill \\ \hfill & =\mathrm{P}(\mathrm{Ob}\mid \mathrm{Dx})[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Ob},\mathrm{Dx}\left)\right]\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{Dx})\hfill \end{array}$$

We assumed

$$\mathrm{P}(\mathrm{T}\mid \mathrm{Ob},\mathrm{Dx})=\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})$$

and

$$\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{Dx})=\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})$$

Substituting in we get

$$\mathrm{P}(\overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\mid \mathrm{Dx})=\mathrm{P}(\mathrm{Ob}\mid \mathrm{Dx})[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})$$

We know that

$$\mathrm{P}(\mathrm{Ob}\mid \mathrm{Dx})=\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}\left(\mathrm{Ob}\right)∕\mathrm{P}\left(\mathrm{Dx}\right)$$

Substituting in we get

$$\mathrm{P}(\overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\mid \mathrm{Dx})=\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}\left(\mathrm{Ob}\right)[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})∕\mathrm{P}\left(\mathrm{Dx}\right)$$

Similarly, it can be shown that

$$\mathrm{P}(\overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\mid \overline{\mathrm{Dx}})=\mathrm{P}(\overline{\mathrm{Dx}}\mid \mathrm{Ob})\mathrm{P}\left(\mathrm{Ob}\right)[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})∕\mathrm{P}\left(\overline{\mathrm{Dx}}\right)$$

We can now substitute into the original equation for $\mathrm{P}(\mathrm{Dx}\mid \overline{T},\mathrm{Ob},\mathrm{S})$ to get the following:

$$\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})=\frac{\left[\frac{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}\left(\mathrm{Ob}\right)[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})}{\mathrm{P}\left(\mathrm{Dx}\right)}\right]\mathrm{P}\left(\mathrm{Dx}\right)}{\left[\frac{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}\left(\mathrm{Ob}\right)[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})}{\mathrm{P}\left(\mathrm{Dx}\right)}\right]\mathrm{P}\left(\mathrm{Dx}\right)+\left[\frac{\mathrm{P}(\overline{\mathrm{Dx}}\mid \mathrm{Ob})\mathrm{P}\left(\mathrm{Ob}\right)[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})}{\mathrm{P}\left(\overline{\mathrm{Dx}}\right)}\right]\mathrm{P}\left(\overline{\mathrm{Dx}}\right)}$$

which simplifies to

$$\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})=\frac{\mathrm{P}(\mathrm{DX}\mid \mathrm{Ob})[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]+\mathrm{P}(\overline{\mathrm{Dx}}\mid \mathrm{Ob})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}$$

We know that

$$\mathrm{P}(\overline{\mathrm{Dx}}\mid \mathrm{Ob})=1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})$$

Substituting in we get

$$\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})=\frac{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]+[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\right][1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}$$

Now, we want to solve for P(Dx|Ob).

$$\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})=\frac{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})}{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]}\left\{\mathrm{P}\right(\mathrm{Dx}\mid \mathrm{Ob}\left)\right[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})]+[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\left]\right[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})\left]\right\}$$

$$\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})=\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})+\frac{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})}{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]}[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\right][1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]$$

$$\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})[1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\right]=\frac{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})}{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right]}[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\right][1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]$$

$$\frac{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})}{[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\right]}=\frac{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right][1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\right]}$$

$$\frac{[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\right]}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})}=\frac{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right][1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\right]}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}$$

$$\frac{1}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})}-1=\frac{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right][1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\right]}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}$$

$$\frac{1}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})}=\frac{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right][1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\right]}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}+1$$

$$\frac{1}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})}=\frac{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right][1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\right]+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}$$

Equation 1:

$$\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})=\frac{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}{[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx}\left)\right][1-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S}\left)\right]+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{T}},\mathrm{Ob},\mathrm{S})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}}\left)\right]}$$

The derivation of Equation 2 for $\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})$ parallels the derivation of Equation 1 for P(Dx|Ob).

APPENDIX 2

Below we provide a detailed derivation of Equation 3, which is used to estimate P(S|T).

Both for women who were obese and those who were not, we directly observe the number of cases that were prenatally diagnosed where the pregnancy was terminated (M₁ and M₂) among women with estimated dates of delivery by December 31^st, 2005 (the last time women were asked about prenatal diagnosis). These counts are equal to the following:

$${\mathrm{M}}_1={\mathrm{N}}_1\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})\mathrm{P}(\mathrm{S}\mid \mathrm{T})$$

$${\mathrm{M}}_2={\mathrm{N}}_2\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})\mathrm{P}(\mathrm{S}\mid \mathrm{T})$$

where N₁ is the number of obese women who carried fetuses with spina bifida that reached a gestational age of at least 13 weeks (approximately the earliest gestational age at which spina bifida could be prenatally diagnosed) (21) and N₂ is the corresponding number of non-obese women. N₁, N₂, and the probabilities in the equations above refer to pregnancies with estimated due dates in the same timeframe as the pregnancies contributing to M₁ and M₂.

We can rearrange the equations and add them together to get the following:

$${\mathrm{N}}_1+{\mathrm{N}}_2=\frac{{\mathrm{M}}_1}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}\left(T\mid \mathrm{Dx}\right)\mathrm{P}\left(S\mid T\right)}+\frac{{\mathrm{M}}_2}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})\mathrm{P}\left(T\mid \mathrm{Dx}\right)\mathrm{P}\left(S\mid T\right)}$$

Similarly, we directly observe the number of liveborn and stillborn cases in the study born to obese and not obese women (Q₁ and Q₂) with estimated dates of delivery by December 31^st, 2005. Q₁ is equal to the following:

$${\mathrm{Q}}_1={\mathrm{N}}_1\left[\mathrm{P}\right(\overline{\mathrm{Dx}}\mid \mathrm{Ob}\left)\mathrm{P}\right(\overline{\mathrm{T}}\mid \overline{\mathrm{Dx}}\left)\mathrm{P}\right(\mathrm{S}\mid \overline{\mathrm{T}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\overline{\mathrm{T}}\mid \mathrm{Dx}\left)\mathrm{P}\right(\mathrm{S}\mid \overline{\mathrm{T}}\left)\right]$$

Where N₁ and the probabilities in the equation refer to the same timeframe as Q₁. We know that

$$\mathrm{P}(\overline{\mathrm{Dx}}\mid \mathrm{Ob})=1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})$$

and

$$\mathrm{P}(\overline{\mathrm{T}}\mid \overline{\mathrm{Dx}})=1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})$$

and

$$\mathrm{P}(\overline{\mathrm{T}}\mid \mathrm{Dx})=1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})$$

Substituting in we get

$${\mathrm{Q}}_1={\mathrm{N}}_1\left\{\right[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\left]\right[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})\left]\mathrm{P}\right(\mathrm{S}\mid \overline{\mathrm{T}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\right[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})\left]\mathrm{P}\right(\mathrm{S}\mid \overline{\mathrm{T}}\left)\right\}$$

By rearranging, we get

$${\mathrm{Q}}_1={\mathrm{N}}_1\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})\left\{\right[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\left]\right[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})]+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\right[1-\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})\left]\right\}$$

$${\mathrm{Q}}_1={\mathrm{N}}_1\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]$$

$${\mathrm{Q}}_1={\mathrm{N}}_1\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]$$

Similarly, Q₂ can be shown to be equal to the following:

$${\mathrm{Q}}_2={\mathrm{N}}_2\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]$$

We can rearrange the equations and add them together to get the following:

$${\mathrm{N}}_1+{\mathrm{N}}_2=\frac{{\mathrm{Q}}_1}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}+\frac{{\mathrm{Q}}_2}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}$$

Next, we set the two expressions for N₁+N₂ equal to each other and solve for P(S|T) as follows:

$$\frac{{\mathrm{M}}_1}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})\mathrm{P}(\mathrm{S}\mid \mathrm{T})}+\frac{{\mathrm{M}}_2}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})\mathrm{P}(\mathrm{S}\mid \mathrm{T})}=\frac{{\mathrm{Q}}_1}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}+\frac{{\mathrm{Q}}_2}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}$$

$$\frac{1}{\mathrm{P}(\mathrm{S}\mid \mathrm{T})}\left[\frac{{\mathrm{M}}_1}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})}+\frac{{\mathrm{M}}_2}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})}\right]=\frac{{\mathrm{Q}}_1}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}+\frac{{\mathrm{Q}}_2}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}$$

Thus Equation 3 equals the following:

$$\mathrm{P}(\mathrm{S}\mid \mathrm{T})=\frac{\frac{{\mathrm{M}}_1}{\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})}+\frac{{\mathrm{M}}_2}{\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}})\mathrm{P}(\mathrm{T}\mid \mathrm{Dx})}}{\frac{{\mathrm{Q}}_1}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \mathrm{Ob}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}+\frac{{\mathrm{Q}}_2}{\mathrm{P}(\mathrm{S}\mid \overline{\mathrm{T}})[1-\mathrm{P}(\mathrm{T}\mid \overline{\mathrm{Dx}})+\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \overline{\mathrm{Dx}})-\mathrm{P}(\mathrm{Dx}\mid \overline{\mathrm{Ob}}\left)\mathrm{P}\right(\mathrm{T}\mid \mathrm{Dx}\left)\right]}}$$

We assume the selection probabilities based on women with estimated dates of delivery by December 31^st, 2005 do not change over time and the weights based on these probabilities can be applied to cases whose mothers with estimated dates of delivery after that date.