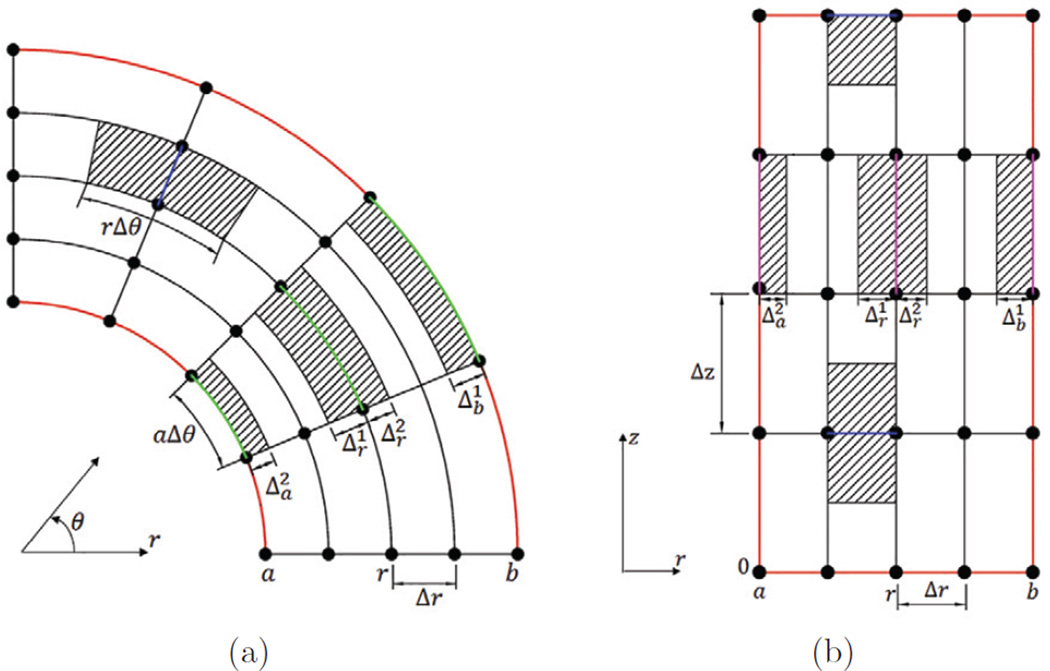
Fig. 1.

(a) Schematic of patches (hatched areas) associated with radial springs and circumferential springs in (r, θ) plane. Two boundaries of the tube shown here are the inner (r = a) and the outer surface (r = b). In (r, θ) plane, the patch of a radial spring connected by nodes (r, θ, z) and (r + Δr, θ, z) is (r, r + Δr) × (θ − 0.5Δθ, θ + 0.5Δθ). The patch of a circumferential spring connected by the nodes (r, θ, z) and (r, θ + Δθ, z) is $(r-{\mathrm{\Delta }}_r^1,r+{\mathrm{\Delta }}_r^2)\times (\theta ,\theta +\mathrm{\Delta }\theta )$ for a < r < b, $(r-{\mathrm{\Delta }}_r^1,r)\times (\theta ,\theta +\mathrm{\Delta }\theta )$ for r = b, and $(r,r+{\mathrm{\Delta }}_r^2)\times (\theta ,\theta +\mathrm{\Delta }\theta )$ for r = a. Here ${\mathrm{\Delta }}_r^1=r-\sqrt{r(r-\mathrm{\Delta }r)}$ and ${\mathrm{\Delta }}_r^2=-r+\sqrt{r(r+\mathrm{\Delta }r)}$ are such that the circumferential patch is partitioned into two equal volumes. (b) Schematic of patches (hatched areas) associated with radial springs and axial springs in (r, z) plane. The boundaries of the tube shown here are: the inner (r = a); outer (r = b); lower (z = 0); and upper (z = l) surfaces. In the (r, z) plane, the patch of a radial spring connected by nodes (r, θ, z) and (r + Δr, θ, z) is (r, r + Δr) × (z − 0.5Δz, z + 0.5Δz) for 0 < z < l; (r, r + Δr) × (z − 0.5Δz, z) for z = l and (r, r + Δr) × (z, z + 0.5Δz) for z = 0. The patch of an axial spring connected by nodes (r, θ, z) and (r, θ, z + Δz) is $(r-{\mathrm{\Delta }}_r^1,r+{\mathrm{\Delta }}_r^2)\times (z,z+\mathrm{\Delta }z)$ for a < r < b, $(r-{\mathrm{\Delta }}_r^1,r)\times (z,z+\mathrm{\Delta }z)$ for r = b, and $(r,r+{\mathrm{\Delta }}_r^2)\times (z,z+\mathrm{\Delta }z)$ for r = a.