Abstract
Single Tracking Location (STL) Shear wave Elasticity Imaging (SWEI) is a method for detecting elastic differences between tissues. It has the advantage of intrinsic speckle bias suppression compared to Multiple Tracking Location (MTL) variants of SWEI. However, the assumption of a linear model leads to an overestimation of the shear modulus in viscoelastic media. A new reconstruction technique denoted Single Tracking Location Viscosity Estimation (STL-VE) is introduced to correct for this overestimation. This technique utilizes the same raw data generated in STL-SWEI imaging. Here, the STL-VE technique is developed by way of a Maximum Likelihood Estimation (MLE) for general viscoelastic materials. The method is then implemented for the particular case of the Kelvin-Voigt Model. Using simulation data, the STL-VE technique is demonstrated and the performance of the estimator is characterized. Finally, the STL-VE method is used to estimate the viscoelastic parameters of ex-vivo bovine liver. We find good agreement between the STL-VE results and the simulation parameters as well as between the liver shear wave data and the modeled data fit.
Index Terms: ARFI, Acoustic Radiation Force, Shear wave Elastography Imaging, Single Tracking Location, Viscoelasticity, Liver Fibrosis
I. Introduction
The elastic modulus of human liver has been shown to correlate with the disease state [1] and has been explored for its diagnostic value [2]. Additionally, shear viscosity has been reported to correlate with disease state in rat liver fibrosis [3] and in human liver fibrosis [4]. However, the measurement of liver viscosity, in both human [4] [5] and rat livers [4], has yet to be demonstrated as diagnostically useful. Nevertheless, it has been suggested that the choice of viscoelastic model may lead to inaccuracies that obscure the utility of viscoelastic measurements [4] [5] [4]. Therefore, further investigations are warranted. Regardless, it is important to note that failure to account for shear viscosity biases measurements of shear modulus in systems that use dynamic shear excitations. Therefore, techniques that can non-invasively estimate shear viscosity, as well as shear modulus, are of particular interest.
Non-invasive ultrasound measurement of shear viscosity is a topic of active research. Several ultrasound elastography techniques currently exist that can be used to determine the shear viscosity of a material. These include direct inversion of the Helmholtz equation from vibrating needle stimulation displacement data [6], exciting tissues with monochromatic shear waves as in Shear Wave Dispersion Ultrasound Vibrometry (SDUV) [7], measuring the dispersion of crawling waves [8], observing the creep response of tissues under acoustic radiation force (ARF) [9], and calculating the relaxation time constant [10] following ARF excitation. The effect of viscosity on transient shear waves used in Supersonic Shear Wave Imaging (SSI) has also been investigated [11]. In this work, we introduce a new technique based on Single Tracking Location Shear Wave Elasticity Imaging (STL-SWEI) imaging.
STL-SWEI estimates the shear modulus of a material by observing the passage of two acoustic radiation force impulse (ARFI) induced shear waves that are applied at two laterally separated locations [12]. While the location of the applied ARFI is varied, the location used for observing the two waves is kept fixed. The observed shear wave signals are then cross-correlated to find the time delay between them and the shear wave speed is estimated. This approach may be contrasted with Multiple Tracking Location (MTL) SWEI techniques in which the observation location is varied and the ARFI focus is fixed. In STL methods, the effect of uncertainty in the tracking location, due to randomness of the tracked speckle, is suppressed. As a result, STL-SWEI produces robust, reproducible shear modulus estimates [13]. However, these estimates are based on the cross-correlation of the shear wave signals. This estimator assumes a purely elastic material model. The result, as shown here, is an overestimation of the shear modulus. In order to correctly reconstruct the shear modulus, a method that accounts for the shear viscosity is required.
In this work, the STL-SWEI technique is extended to viscosity estimation using a new post-processing method denoted STL Viscosity Estimation (STL-VE). First, the theory behind this inversion method in the context of the STL-SWEI imaging problem is developed. Next, a software implementation of the STL-VE reconstruction technique is presented. Third, simulated shear wave velocity data is used to demonstrate the effect of viscosity on the shear modulus measured by the STL-SWEI (cross-correlation) and the STL-VE reconstruction methods. Additionally, the effect of varying the tracking offset, noise level, excitation geometry, and acquisition time is explored. Finally, the STL-VE method is applied to ex vivo bovine liver and good agreement between the model and real shear wave data is demonstrated.
II. Theory
A. The Kelvin Voigt Model of Viscoelasticity
The Kelvin-Voigt model is a classical mechanical viscoelastic model given in the frequency domain by [14]:
| (1) |
Here σ is the stress and ε is the strain and ω is the angular frequency. The value G* is known as the complex shear modulus. It has a real part, G′, and an imaginary part, G″, known as the shear storage and shear loss moduli, respectively. In the general case, both of these quantities are functions of angular frequency, ω. In the Kelvin-Voigt model, the storage modulus is taken to be constant with G′ = μ, with μ referred to as the shear modulus. The loss modulus for the Kelvin-Voigt model is a linear function of frequency G″ = ωη where η is the shear viscosity.
In a viscoelastic medium, the wavenumber, k, is a complex quantity. Not only does the wavenumber include the reciprocal of the shear wave length, λ, as its real part, but the wavenumber also includes attenuation in the form of an imaginary part. The separate real and imaginary parts of the wavenumber can be derived by noting the relationship with ρ representing the density of the material. With some manipulation, it can be shown that
| (2) |
Here |G*| is the magnitude of the complex modulus. Substituting μ + iωη for G* yields the wavenumber for the Kelvin-Voigt model given by
| (3) |
and
| (4) |
where kr is the real part and ki the imaginary part of the wavenumber. We will define the shear wave speed as the inverse of the real part of the wavenumber multiplied by the angular frequency (i.e. the wave speed is taken to be a real quantity not a complex one). Therefore, for the Kelvin-Voigt model the shear wave speed may be expressed as
| (5) |
For relatively low frequency applications (i.e. where ω2η2 ≪ μ2), the following low order approximations are helpful in determining the contributions of η and μ to the wave number:
| (6) |
It is immediately clear that the viscosity primarily contributes to the attenuation and not the phase of the shear wave in low frequency applications.
B. The STL-SWEI Estimation Problem
The STL-SWEI technique can be thought of as a delay estimation problem. The geometry employed by the technique is depicted in Figure 1. Two push, or excitation, locations are separated by some distance Δx at an offset of x0 from the tracking location. These excitations are generated by an acoustic radiation force (ARF) impulse using the same ultrasound excitation frequency, aperture, and element delays relative to the lateral focus. It is assumed that both excitations are equal in shape but not necessarily amplitude, i.e. they contain the same spatial frequency content (amplitude and phase) up to a constant amplitude scaling factor. The transient shear waves that result from the ARF excitations are tracked at the observation location using a standard pulse-echo sequence and a speckle tracking algorithm. The shear modulus of the material is determined by measuring the arrival time difference (or some similar metric) between shear waves generated from the application of acoustic radiation force at the two push locations.
Fig 1.
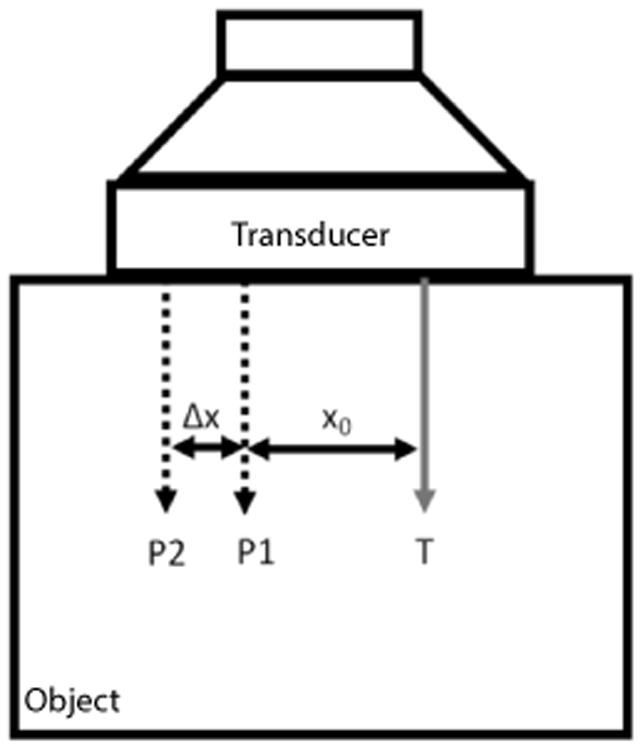
The configuration of the Single Track Location (STL) experiment. A transducer is placed on top of a block of material. The tracking location is denoted (T), (P1) is the 1st push location, and (P2) is the 2nd push location. The distance between the (T) and (P1), denoted x0, is referred to as the tracking offset and Δx is the push to push distance.
The two spatial parameters, x0 and Δx, are not fixed and may be chosen as imaging parameters. The parameters are left unfixed because without prior knowledge of the material properties, it is not possible to predict what particular spacings will yield acceptable tracked shear wave data (shear wave traces). Here we define acceptable shear wave traces as those that yield modulus estimates that are not significantly biased by truncation of the wave (truncation bias). Since the shear wave acquisition occurs over a finite period of time, it is possible that the beginning or the end of the disturbance may not be sampled. If the end of the disturbance is missing, then simply increasing the acquisition time may be adequate. However, if the beginning of the shear wave disturbance is not sampled then the excitation location must be moved further away from the tracking location to allow adequate time to switch between generating the excitation and tracking it. This is accomplished by increasing x0. It may then be necessary to decrease Δx to prevent truncation of the tail of the shear wave or increase the acquisition time. If the acquisition time must be kept short (e.g. due to motion concerns) then decreasing Δx may be the only option. Ideally, if the wave is adequately sampled then changing parameters such as x0 and Δx should not change the measurement (i.e. the measurement should reflect the underlying properties of the material and not the imaging system/parameters). We will show that this ideal is nominally violated when a linear elastic estimator is applied to viscoelastic materials.
We begin by developing a mathematical model of the measurement process. For the linear elastic case, the STL-SWEI problem can be reduced to determining the time delay between the two waves:
| (7) |
Here s1(t) is the signal observed following the first push, s2(t) is the signal observed following the second push, n1(t) represents noise in the estimate of s1, and n2(t) is the noise in the estimate of s2. The maximum likelihood estimator for this problem (assuming Gaussian distributed noise) is known to be the time index of the peak of the cross-correlation, h(t) = s2(t) * s1(−t) of the two signals with * representing the convolution operation [15]. This may be expressed as
| (8) |
It should be noted that these waves are approximately cylindrical and, as a result, the amplitude of these waves will be reduced by , where r is the propagation distance, regardless of attenuation. A constant geometric factor between the two waves does not alter the validity of this equation. A limitation of this method is that it does not consider the dispersion that occurs in viscoelastic materials. To demonstrate the shortcomings of this estimation method in viscoelastic materials, consider (8) in the frequency domain. Letting h(τ) = ℱ−1 {H (ω)} represent the cross-correlation in (8), with ℱ−1 the inverse Fourier Transform, yields:
| (9) |
Here H(ω) = AH(ω)e−ik(ω)Δx with AH(ω) the amplitude of the cross-spectral density. Since the cross-correlation is between two real-valued signals the imaginary part of the integrand may be ignored. Therefore, (9) may be written as:
| (10) |
In the purely linear elastic case, , with material density ρ, shear modulus μ, and shear wave speed cs. This yields:
| (11) |
The maximum of the right hand expression must occur at since AH(ω) is non-negative for all ω and is maximized for all values of ω only at . This yields the correct shear wave speed in purely elastic materials. However, when a viscoelastic model for the material is used, such as the Kelvin-Voigt model, (11) becomes:
| (12) |
Here the shear wave speed is now a function of frequency and finding the solution to (11) requires prior knowledge of AH(ω). In fact, the measured time delay is a weighted minimization of , with AH(ω) serving as a weighting function. Therefore, without knowing AH(ω), the relationship between the peak of the cross-correlation and cs(ω) is not clear.
One approach to eliminate this dependence on AH(ω) is to interrogate the material with monochromatic shear waves for which AH(ω) = δ(ω − ω0). In this case, . Subsequently, one could repeat the monochromatic interrogation at numerous frequencies and reconstruct cs(ω). This is referred to as vibrometry in the context of Shear Wave Dispersion Ultrasound Vibrometry (SDUV) [7]. However, an alternate reconstruction can be applied to the STL-SWEI measurements without deferring to this monochromatic limit.
C. STL Viscoselastic Estimation via Spectroscopy
Conceptually, spectroscopy is a method for determining the change in shear wave phase as a function of frequency in the context of transient waves. It differs from vibrometry in the sense the frequency spectra are derived from broadband, transient, excitations rather than separate monochromatic excitations. STL-SWEI offers a unique approach to generating shear wave spectrograms. First consider S1(ω) = ℱ{s1(t)} written in terms of its amplitude and phase:
| (13) |
Here A0(ω)eiϕ(ω) is the magnitude A0(ω) and the phase ϕ(ω) of the original ARF excitation. e−ki(ω)(x0+xe) models the transformation between the initial ARF exciation and S1(ω) with x0 is the distance between the pushing location and the tracking location, and random variable xe is the error in x0 due to speckle bias. This speckle bias arises due to the fact that bright speckle is preferentially tracked when the shear wave velocity is being determined via Window Normalized Cross-Correlation (WNCC) of the original RF data [13], [16]. This bright speckle need not be along the beam axis and, therefore, our actual tracking location is truly x0 + xe. For S2(ω) = ℱ{s2(t)} we have:
| (14) |
Here β is a scaling factor that absorbs the component of the asymptotic cylindrical wave approximation. Although xe is random and unknown a priori, since the tracking location has not changed, it takes the same value in (13) and (14). By taking the cross-spectral density, H(ω), the bias, the tracking offset, and the initial phase of the two signals are all eliminated,
| (15) |
This elimination of the bias (for the real part of the wavenumber) is the strength of the STL-SWEI method over MTL techniques. We may now generate a spectrogram, P(ω), by considering the ratio of the cross-spectral density to the power of the signal generated in the first shear wave excitation.
| (16) |
We may use our linear propagation model to relate the spectrogram to the material properties. Substituting (15) and (17) into (19) yields:
| (17) |
Using the definition of the complex wave-number results in:
| (18) |
The real part of the wavenumber may be found by taking the phase of the spectrogram. Subsequently, the shear wave speed as a function of frequency may be determined and, if desired, a viscoelastic model may be fit to this data to project the shear wave speed data onto a lower dimensional space. In the setting of STL-SWEI, this formulation benefits from having no explicit dependence on AH(ω) or on the speckle bias. This suggests that STL-SWEI may produce improved spectrograms compared to MTL techniques. However, this formulation ignores the noise content of the measured signals. Additionally, the model used here is for plane waves. It is also possible to relate other models to the spectrogram (i.e. cylindrical waves). We will see that for a cylindrical source at the distances used in STL-SWEI, this alternative model will be necessary.
The approach presented thus far has been derived in an ad hoc way. It is known that the two shear waves contain this spectral information but there is no guarantee that this solution is the optimal method for extracting viscoelastic parameters from the shear waves. As an alternative, we now introduce an implementation of STL-VE based on Maximum Likelihood Estimation, as a more formal and robust solution to the extraction of viscoelastic parameters from STL-SWEI shear wave data.
D. Single Tracking Location Viscosity Estimation by Maximum Likelihood Estimation
The STL-SWEI problem (7), may be formalized in vector notation by considering the two noise corrupted measured signals,
| (19) |
Here y⃗1 and y⃗2 are the measured velocity time series with s⃗1 and s⃗2 the underlying signals, respectively. The noise terms n⃗1 and n⃗2 are assumed to be zero mean, additive white Gaussian noise (AWGN). In this notation, each element of the vectors corresponds to a different time point. The elasticity measurement is achieved by assuming a model relating the two signals, s⃗1 and s⃗2. For plane waves in a purely elastic media, s⃗2 is simply a time delayed replica of s⃗1. In viscoelastic materials, the relationship is best described by considering the waves in the frequency domain. In the vector notation, the Fourier Transform is represented as a matrix multiplication. Let the matrix ℱ represent the Fourier Transform and ℱ−1 the Inverse Fourier Transform.
| (20) |
Here S⃗1 is the Fourier Transform of s⃗1. The Inverse Fourier Transform of the spectrum of s⃗2 is given by:
| (21) |
Finally, the two spectra, S⃗1 and S⃗2 are related by:
| (22) |
where a filter, K (the “Wave Filter”), is applied to S⃗1 to yield S⃗2. This filter contains information related to both the material properties and the geometry of the propagating wave. Using (20), (21), and (22) we can relate the two signals in the time domain.
| (23) |
Noting that s⃗1 = y⃗1 − n⃗1, we can combine the two equations in (19) with (23) to arrive at a representation of s⃗2 in terms of the actual received signal y⃗1.
| (24) |
The second term, ℱ−1Kℱn⃗1 denotes the transformation of the noise upon application of the estimated Wave Filter. By combining (19) and (24) we arrive at the relationship between the total noise and the difference in the signals,
| (25) |
Here n⃗3 is the noise in the estimated filtered difference between the two measured signals. To determine the maximum likelihood estimator for this problem we need only determine the probability density function of n⃗3.
| (26) |
| (27) |
| (28) |
Here and are the variances of the noise for the first and second shear wave signals, respectively. Rather than evaluate this integral explicitly, we will assume the probability density (28) is still Gaussian and zero mean. This assumption is valid in linear materials and when the variance is small. The latter case follows directly from the fact that no noise in the first signal leads directly to n⃗3 = n⃗2. The former case can be seen by considering that the application of K leads only to a time shift on n⃗1 which is simply a different realization of n⃗1. As a result, (28) becomes
| (29) |
C is some constant and υ3 is the standard deviation of the new noise distribution. For the linear elastic case, . This does not hold for the viscoelastic case where K attenuates the noise n1. Therefore, , in general. However, it is not necessarily the case that < n⃗3 >= 0⃗. We will proceed as if this is true and then in simulation demonstrate the limits of this assumption.
Continuing with the Gaussian distribution assumption (29), consider the joint probability of measurement y1 and y2. Defining the residual, r⃗(K) = y2 − ℱ−1Kℱy⃗1 = n⃗3, yields
| (30) |
If L pairs of shear wave traces are obtained then the joint probability function over the entire set of samples is
| (31) |
Here P(y⃗1l | y⃗2l∀l) is the joint probability function for all the data received taken together with l the index of the trace pair. To find K, we want to find the value of K that maximizes (31). Taking the natural log of (31) and expressing the above criterion mathematically yields
| (32) |
Here K̂ is the estimate of K. Simplifying further yields,
| (33) |
This formulation suggests that the optimal value of K is obtained by minimizing the expectation value of the squared residual, < r⃗(K)2 >. This is a least square problem. Note that this result is distinct from calculating the expectation value alternatives such as spectroscopy where K is found by calculating the expectation value . This equation holds for any viscoelastic model. Parameterizing K according to some model, such as the Kelvin-Voigt model, allows for the determination of particular model parameters. It should be noted that an estimator tailored to a specific model may also be achieved and might be more accurate for the specific case of that model. However, the ability to apply multiple models to the estimator is desirable since an optimal viscoelastic model for biological tissues is not established. Let Θ represent the parameters of some viscoelastic model. The parameter estimate θ̂ is given by
| (34) |
We now turn our attention to the form of filter K.
E. The Form of the Wave Filter K
The exact form of the filter K depends on both the geometry of the excited wave and on the material properties. For convenience, K will now be treated as a continuous function. In our model, we will assume K is given in the following form:
| (35) |
Here θ are the parameters of interest with θm representing the material parameters and θg the geometry parameters. G* is the complex modulus, and Γ is the wave function for the given geometry. x0 and x1 = x0 + Δx are the distance between the tracking location and the pushing location for the first and second shear wave excitation, respectively.
Two different wave functions are utilized, one function for plane waves and the other for cylindrical waves. The plane wave case is given by
| (36) |
Here ρ is the density of the material and is assumed to have a particular constant value equal to the density of water. Therefore, it is not included in the parameters to be found, θm. The parameter β ∈ θg is included to compensate for variability in the excitation amplitude (e.g. due to variation in tissue attenuation, acoustic output, etc.). While this model is computationally convenient, the excitation generated by acoustic radiation force has a limited elevational extent and, therefore, a cylindrical wave assumption may be closer to reality. In that case, we may use
| (37) |
to derive K for a cylindrical excitation. Here is the Hankel function for an outward traveling cylindrical wave of zeroth order. It should be noted that in the asymptotic limit the two models are computationally equivalent. Let us assign different β factors to the two models: β1 for the plane wave and β2 for the cylindrical wave model. In the asymptotic limit the cylindrical wave model becomes
| (38) |
Since is constant, the product is also a constant. Making the assignment , the asymptotic cylindrical wave model becomes
| (39) |
Thus, the two models are equivalent.
F. MTL Estimator Bias
In deriving the above estimators, an STL based model of the tracking problem has been assumed. It may seem that these estimators are equally applicable to the MTL problem. However, it can be shown that the application of these estimators to MTL data leads to biased estimates. This includes the appearance of viscoelasticity in materials that are, in fact, purely Hookean. To see this, consider the problem of estimating the elastic spectrogram (17) in the absence of thermal noise but in the presence of speckle bias. Making the assumption that the speckle bias is an AWGN source and that the first and second excitation have different realizations of the noise, the estimate of the spectrogram is now
| (40) |
If xe1 and xe2 are drawn from a Gaussian distribution with standard deviation σx then the standard deviation of the distribution generating xe3 is √2σx. The MLE estimator derived for the STL problem above is optimized for reducing the effect of thermal noise in the velocity measurement, but was not designed to handle this tracking position noise. When there is no noise, all of these estimators are essentially aggregating the spectrogram over some number of trace pairs. Mathematically, the spectrogram is estimated as
| (41) |
Using (40) the expectation value of the spectrogram is
| (42) |
Here each , with respect to l, is an independent realization of the random variable and Pactual(ω) is the true spectrum for the material. The term serves to multiply the true spectrum by some speckle bias induced spectrum. In the limit, L approaches ∞ (i.e. we have infinite number of shear wave trace pairs) this is simply the expectation value . If this expectation value were one, then there would be no difference in using STL or MTL for measuring viscosity. However, this expectation value is not necessarily equal to one and is also frequency dependent. Consider the propagation of error equation for this expectation value
| (43) |
where Xe3 is the random variable from which the instance xe3 is drawn. Since the distribution is Gaussian with standard deviation √2σx this becomes
| (44) |
Combining (45) and (42) yields,
| (45) |
So the presence of speckle bias adds a second order in the k term to the spectrogram. For linear elastic materials, this has the effect of producing a frequency dependent loss. Consider the linear case . The resulting spectrogram is given as
| (46) |
Thus, there is now a loss term that has a second order dependence on frequency that is not from true viscosity but instead from estimation errors. For cylindrical waves, the situation is more complicated and the STL case is not completely immune to the effect of this tracking location variance. This tracking location error will be examined for both STL and MTL cases in simulation.
III. Methods
A. Implementation of the MLE based Non-Linear Least Squares Solver
The MLE based reconstruction of STL-VE may be implemented using a non-linear least squares (NLLS) routine. In this work, we use the Gauss-Newton method to solve the Non-Linear Least Square (NLLS) problem [17]. The method is iterative and a new residual vector is calculated at each step based on the current value of some parameters. A least squares problem is then solved to determine a parameter update and the iteration is complete. For this problem, the challenge is in describing the derivatives of the residual with respect to the parameters that we are attempting to solve for. This aspect is problem specific and requires knowledge of the form of the residual and the model relating the model parameter vector θ to the residual. First consider the form of the residual, r⃗,
| (47) |
The Jacobian matrix J is given by the derivative of the residual with respect to the parameters.
| (48) |
Using the Y⃗1 = ℱy⃗1 and (47), the Jacobian becomes
| (49) |
The problem of defining the algorithm is reduced to determining the derivatives of the filter, K, with respect to the parameters of the model being used.
B. Jacobian of the Viscoelastic Problem
Consider the equations for the frequency domain filter, K, given for both the plane and cylindrical wave cases in (36) and (37), respectively. The derivative of the K with respect to β is straightforward and yields,
| (50) |
To compute the derivatives with respect to the viscoelastic model parameters it is useful to expand the partial derivative of K by the chain rule.
| (51) |
Here θj is a particular parameter of the material parameter subset θm and k is the wave number with . Only the final derivative in the chain depends on the particular viscoelastic model. This greatly simplifies the implementation of the algorithm because the unique description of any viscoelastic model is given simply by taking the partial derivatives of G* with respect to the model parameters.
We will refer to the first derivative on the right hand side of (51) as the wave geometry derivative. This term depends on the waves geometry alone. For the plane wave case, this is given by
| (52) |
Alternatively, if the wave geometry is cylindrical, then this derivative is given by
| (53) |
The second derivative on the right hand side of (51) is given by
| (54) |
regardless of geometry or viscoelastic model. The final derivative depends on the viscoelastic model. For the Kelvin-Voigt model the parameter vector with the material property subset . For this model the final derivative in (51) is given by
| (55) |
for the θj = μ and the θj = η cases, respectively.
| (56) |
While this MLE algorithm is mathematically rigorous, it is also computationally demanding. The major complication is the number of inverse Fourier transforms required to perform the algorithm. For each pair of traces the inverse Fourier transform must be calculated 3 times (in the case of the Kelvin-Voigt model above). These inverse transforms must be performed during each iteration of the Gauss-Newton method. A GPU based implementation is used to accelerate these calculations.
C. Residual Time Gating and DC Correction
A critical feature of the STL-VE MLE algorithm is the ability to “time gate” the residual vector. In the absence of time gating, the algorithm would attempt to fit zeros from the unsampled parts of the first excitation to the second excitation. Additionally, the end of the first excitation is fit to zeros padded to the end of the second excitation. This is particularly troublesome when the time shift between the two waves is high relative to the number of time samples taken. Applying the time gating to the STL-VE MLE algorithm is straight forward. When calculating the residual, as in (47), the residual vector is also a function of time. Simply multiplying the residual by a rect function that is non-zero only for some range of time acheives the desired result.
In addition to time gating, the MLE implementation allows for the setting of variable DC levels for both the first and second shear wave excitation. This has practical applications for signals with a DC level either from velocity estimation bias or in cases where constant velocity motion (possibly physiological) is present during data collection. These pedestals contribute to the frequency content of the excitation near the end points of the shear wave traces (truncation error). Since this pedestal may vary in value throughout some region of interest, it must be considered separately for each shear wave trace pair (as a local parameter of the trace pair: trace local) in the region of interest. This results in a very large number of variables. In addition, the parameter β may also be considered as a trace local parameter since variations in supply voltage may lead to amplitude differences between excitations that vary with each STL-SWEI A-line. For a typical STL-SWEI data set with 128 A-line and 2048 depth samples, using three trace local parameters (DC1, DC2, β) and two global parameters (μ and η) results in 786434 total parameters. The Hessian matrix of the inverse problem then has 3932164 unique non-zero entries.
D. Inverse Problem Implementation
The inverse problem for the STL-VE MLE was implemented in OpenCL for application to Graphic Processing Unit (GPU) based computation. The first essential component of the implementation are an application specific OpenCL kernel (entry point function) for calculating the contributions of each trace pair to the residual and the Hessian matrix of the inverse problem. This step is referred to as “matrix assembly step” (MAS). The second essential component is a custom implementation of the Biconjugate Gradient (BiCG) method, designed specifically to deal with the sparsity characteristics of this problem. The linear algebra optimizations implemented in this second component are beyond the scope of the paper. Both components were developed as part of our labs in-house GPU based elasticity software (Elasticity Lab, University of Rochester). In addition, to the aforementioned components, our in-house software also provides GPU accelerated windowed normalized cross-correlation (WNCC) and can generate the velocity data needed for the estimations described here in real-time (less than one second to perform all WNCCs).
The optimization of the MAS is achieved by way of built in Fast Fourier Transforms. That is, rather than using an FFT kernel from a pre-built library, a custom FFT function was implemented that is applied to local data store (LDS) memory without returning any data to global memory. As a result, a single call to the MAS can be used to calculate all of the FFTs and IFFTs needed to build the Hessian matrix and the residual vector. 256 threads are required to process each trace pair with samples per trace pair fixed to 128. These 256 threads are designated as a single OpenCL work-group. The same allocation of LDS memory is reused for all FFTs and IFFTs as well as calculating the product of the Jacobian with the transposed Jacobian to arrive at the “local” Hessian for each trace. After the termination of the MAS, the returned local Hessians is summed in a separate function to arrive at the fully assembled Hessian for the BiCG based inversion. Massive parallelism is achieved by simultaneously requesting a number of work-groups equal to the number of trace pairs (typically: 262144). Additionally, the shear wave traces are placed in memory with the slow time samples as the leading dimension with adjacent threads accessing adjacent memory. For data generated from RF, a transposition operation is required since RF data typically has the depth samples as the leading dimension (representing the order in which the scanner generated the data). Additionally, our in-house software calculates WNCC with the A-line index in the leading dimension, necessitating additional transposition operations. Hardware limitations determine the actual level of parallelism achieved.
The focus in this work is on the accuracy of the STL-VE method and not the computational performance. However, it should be noted that despite the number of variables involved, the MLE estimation can be performed in a couple of minutes on a desktop computer with an OpenCL capable GPU.
E. Simulations and Validation
To validate STL-VE method, a Kelvin-Voigt model based simulation similar to that described in [18] was implemented. This 2D simulation utilizes split field equations and perfectly matched layers (PMLs) implemented on a Yee cell grid as originally proposed in [19]. For all simulations, the simulation domain size is 10 cm × 10 cm in the elevational-lateral plane with 1 cm PML on all domain edges. The simulation step size is 0.4 mm spatially and 1 μs temporally. Finally, this implementation includes an iterative guess and revise scheme for calculating time derivatives. This involves first calculating the time update using a linear model and then iteratively solving for the viscoelastic update. The degree to which these alterations improve the performance of the solver is beyond the scope of this work.
To produce the simulated shear wave data, an initial axial velocity is applied to the simulation domain that approximates the focal geometry of the STL-SWEI pushing pulse. Specifically, a Gaussian cylindrical excitation with a lateral full width at half max (FWHM) of 1 mm was applied to the center of the simulation grid. The elevational FWHM varies by experiment. The Gaussian excitation was applied for 300 μs. This excitation time was used to approximate the upper limit of ARFI excitation time used in our ex-vivo experiments. The data from the simulation was sampled at a rate of 7.44 kHz and the central cross-section of the data was saved to disk at each time point. Subsequently, this data is interpolated into a pair “frame-stacks.” Each frame-stack consists of 128 slow time “frames” (representing one point in time) with 128 lateral × 2048 depth samples. The lateral sampling rate was set to 0.17 mm/line and the depth sampling rate of 0.02 mm/sample. This data structure is identical to the data structure used for actual RF in our in-house software. Therefore, the simulation data can be used to directly test the actual code used for processing ultrasound images. The first frame-stack of each pair represents all of the data from each first excitation. The second frame-stack is a matched set of all the data from each second excitation. Here each lateral position in the frame-stack is from a different ensemble. Depending on the computational experiment, the building of these frame-stacks differed. For all experiments, a 1 mm2 region of interest is used for the data analysis.
To examine the effect of varying viscosity on STL-SWEI linear estimation and STL-VE estimation (using the Kelvin-Voigt model with the MLE estimator: KV-MLE method), a number of frame-stack pairs were generated using different first and second push locations. The simulated excitation had a FWHM of 1 mm in both the lateral and the elevational direction. The shear modulus for the simulation was fixed at 2 kPa. This value was chosen because it is within the range of expected shear moduli measured in healthy rat livers using STL-VE and produces excitations that are well contained within the 128 samples at 7.44 kHz (17.2 ms). The shear viscosity was varied from 0.05 to 1 Pa·s. Additionally, the tracking offset was varied from 3.4 mm to 6.8 mm to demonstrate the effect of increasing the tracking offset on the modulus estimate.
The KV-MLE method requires an assumption about the excitation geometry be made. To determine the effect of a mismatch between the excitation geometry and that assumed in the KV-MLE model, a set of simulations with varying excitation geometries was performed. Three particular excitation geometries were used with different (lateral) × (elevational) lengths. The first geometry is a 1 mm × 1 mm FWHM 2-D Gaussian approximating a cylindrical excitation. The second is a 1 mm × 10 cm FWHM 2-D Gaussian excitation approximating a plane wave excitation. Finally, an intermediate geometry using a 1 mm × 5 mm FWHM 2-D Gaussian is applied. Each of these excitations were applied to a simulated materials with a modulus of 2 kPa and shear viscosities ranging from 0.05 to 1 Pa·s. The STL-VE KV-MLE algorithm was applied to each case using either the cylindrical or plane wave model assumption. Additionally, the tracking offset was varied to determine the effect of tracking offset on the estimator bias.
The noise performance of the STL-VE KV-MLE method was examined by corrupting a set of frame-stacks with AWGN. The shear modulus for this experiment was set to either 1 kPa or 2 kPa with a shear viscosity of 1 Pa·s. For this experiment, Δx was fixed at 2.4 mm and x0 was fixed at 5.1 mm. The solution is modeled using the cylindrical wave assumption. The SNR was varied from 0 dB to 20 dB. The noise is intended to simulate thermal noise in the velocity estimate. Five versions of this experiment were performed. In the first the noise is applied evenly to both the first and second excitation data. In the second and third cases, the noise is applied twice to either the first or second excitation data but not both. This demonstrates the limits of the Gaussian noise assumption made in the original MLE derivation. In the fourth case, the noise was applied, but the viscoelastic model was erroneously set to a linear elastic model. This demonstrates the loss of measurement precision when the wrong model is implemented in the reconstruction. In the final case, the noise is applied evenly but a tracking error (consisting of AWGN) is introduced in the data to simulate speckle bias. The standard deviation of the tracking error is set to 0.5 mm to provide an order of magnitude consistent with the RMS tracking errors presented in our previous work [16]. This added tracking error is used to simulate the single and multiple tracking location configurations. When the same realization of noise is used in both frame-stacks then this simulates the STL case. When a different realization of noise is used then a different realization then this simulates the MTL case.
One advantage of using the MLE method is that it is a time domain implementation that is theoretically robust against signal loss due to inadequate sampling. Therefore, we expect that it will outperform naive spectroscopy based implementations when subject to acquisition time constraints. Short acquisition times that truncate the shear waves are typical in imaging experiments where there are limits on the total acquisition time (physiological motion, scanner memory limits, etc.). A set of frame-stacks were generated with varying acquisition end times. Both a 1 kPa, 1 Pa·s and a 2 kPa, 1 Pa·s simulated material were studied. The cut-off time was varied from 5 ms to 17 ms for the 2 kPa material and 7 ms to 17 ms for the 1 kPa material. Modulus and Viscosity estimates for both the KV-MLE and the spectroscopic implementation were then acquired over the range of acquisition times.
F. Ex-vivo Liver Experiment
A bovine liver was acquired and stored in a saline bath and refrigerated overnight allowing the liver/saline system to degas. The following day, the liver was imaged using both STL and MTL beam sequences. At the time of the STL measurement, the temperature of the saline bath was recorded at 18.8°C. The MTL measurement was taken immediately after the STL measurement with a saline temperature of 19.0°C. The combined acquisition time was approximately 10 minutes. The experiment was not intended to replicate physiological conditions. Instead, the liver is used for ascertaining the quality of the MLE model fit to the real shear wave data obtained from a viscoelastic material.
The imaging system for this experiment consisted of a VF7-3 linear array probe operating at 4.21 MHz and connected to Siemens Antares scanner. Analysis of the data was performed using a desktop computer and our in-house elasticity software. The ARF and tracking foci were both set at 2 cm. The ARF excitation was 200 μs and the tracking pulse repetition frequency was 7.44 kHz. The F/# of 3.5 was used to the ARFI excitation and an F/# of 2 was used for the tracking. A dynamic receive F/# of 0.75 was also used.
Eight images were acquired using a track-to-push spacing, x0, of 3.54 mm and a push-to-push spacing, Δx, of 1.24 mm for both the MTL and STL beam sequences. The velocity data (achieved using windowed normalized cross-correlation of the RF data, axially) is averaged over the eight images and then a cross-correlation is applied to each shear wave data pair to arrive at the time delay between the two signals. Subsequently, a modulus map was generated. Next, a region of interest (ROI) was selected from the data set using the modulus map as a guide to find a relatively homogeneous region near the focal depth. The averaged velocity data was then extracted from the ROI and the MLE viscosity estimation technique was applied to determine the the shear modulus and shear viscosity using the assumption of a Kelvin-Voigt model and a cylindrical wave geometry. The “goodness” of the data fits were then compared by examining the resulting coefficient of determination calculated based on the residual (47). Here the WNCC window length was fixed to 0.96 mm.
It should noted that the WNCC window axially averages the velocity data and so a long window tends to limit the variability of the arrival time in the velocity data at the cost of axial resolution. Since MTL is more sensitive to arrival time error, it is expected that MTL based measurements will be severely effected by limited WNCC window length when compared to STL based measurements. Therefore, the post analysis was repeated with WNCC lengths of 0.19 mm, 0.39 mm, and 0.58 mm to determine what effect, if any, the WNCC window length has on estimated modulus and viscosity.
IV. Results
A. Simulation Results
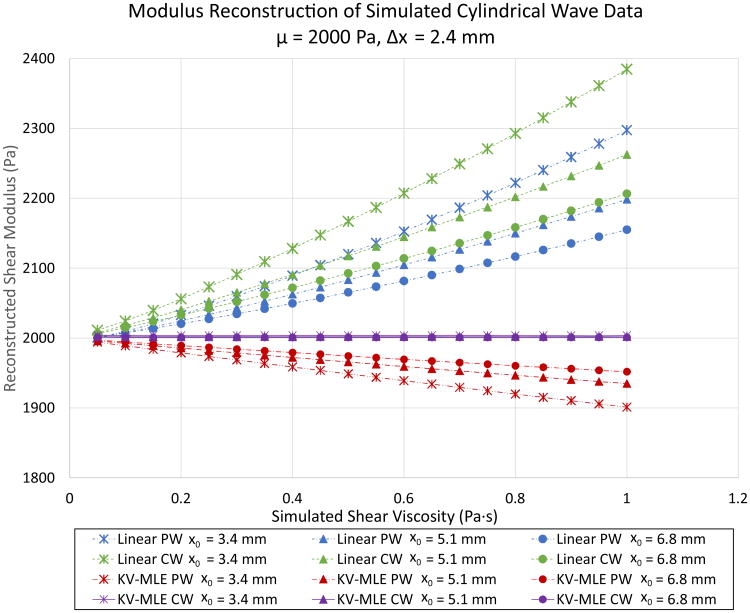
The effect of tracking location, material model, and geometric model on STL modulus estimation is demonstrated in Figure 2. Here a cylindrical wave based simulation has been performed. These results demonstrate that the modulus can be reconstructed faithfully only when the reconstruction algorithm is matched to the material elastic model and to the geometry of the excitation. However, when a Kelvin-Voigt plane wave model is assumed, the modulus becomes a monotonically decreasing function of viscosity. Additionally, the slope of this line increases with decreasing tracking offset. In either wave geometry case, when a linear elastic model is assumed, the modulus estimate becomes a monotonically increasing function of viscosity. The plane wave case generally provides an underestimate of the modulus for a given tracking offset. In the plane and cylindrical wave cases, the shear modulus estimate decreases with increasing tracking offset. There is no dependence of the modulus on the tracking location when the Kelvin-Voigt cylindrical wave simulation is matched with the Kelvin-Voigt cylindrical wave MLE estimator. Importantly, the estimators all converge to the correct modulus as the viscosity decreases. Therefore, these effects are not apparent in linear elastic materials.
Fig 2.
Noiseless simulated cylindrical shear wave data is reconstructed using various geometric and viscoelastic models. Linear elastic and viscoelastic (Kelvin-Voigt Maximum Likelihood Estimation: KV-MLE) estimates are performed for both cylindrical wave (CW) and plane wave (PW) models. The simulated shear modulus is fixed at 2 kPa and the shear viscosity is varied from 0.5 to 1.0 Pa·s. The spacing between the shear wave excitations is fixed at 2.4 mm. The distance between the first shear wave and the tracking location is set to either 3.4 mm, 5.1 mm, or 6.8 mm. Only the KV-MLE CW cases return the correct modulus value. All other cases return erroneous modulus estimates that are dependent on tracking distance.
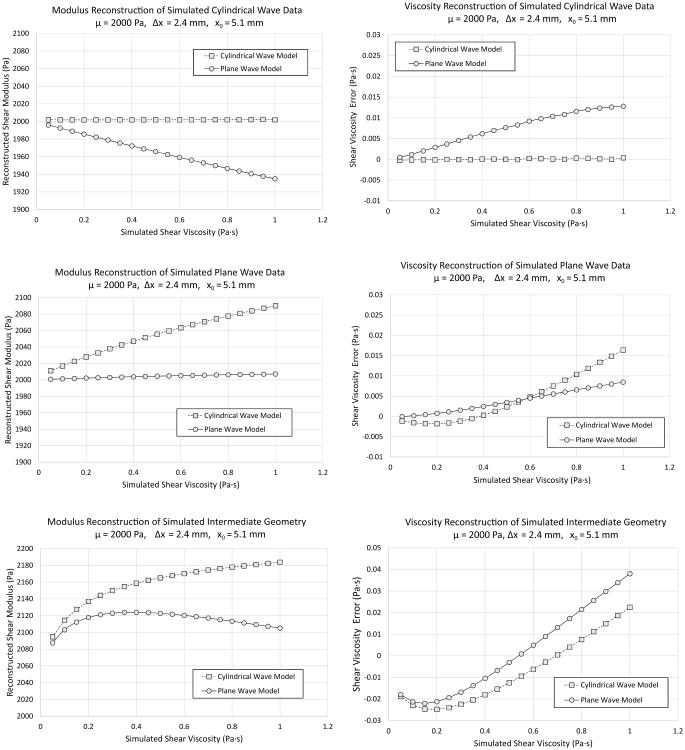
Varying the geometry of the excitation has profound effects on the estimation result. The STL-VE method is applied to cylindrical wave, plane wave, and intermediate (oval shaped) excitations simulations as a function of viscosity in Figure 3. As in Figure 2, matching the cylindrical wave simulation and reconstruction yields a perfect reconstruction of the modulus and viscosity. Plane wave reconstruction of cylindrical simulations yield a modulus result that is a decreasing function of viscosity. It should be noted that this error is never worse than 5% of the actual modulus value. Similarly, plane wave reconstruction of cylindrical wave data yields a viscosity estimate error that is a monotonically increasing function of viscosity. At 1 Pa·s this error is less than 0.015 Pa·s. For the plane wave simulation case, the plane wave based reconstruction yields better results than the cylindrical wave case. When cylindrical waves are assumed for the reconstruction, the modulus estimate is seen to be an increasing function of viscosity. This is the opposite of the plane wave reconstruction of simulated cylindrical waves. This error in the modulus is less than 5% for all viscosities. On the other hand, the viscosity reconstruction of the plane wave simulation using a cylindrical wave assumption yields a viscosity error that is at first decreasing and then increasing with respect to viscosity. However, the magnitude of the error is still less than 0.020 Pa·s for all viscosities. Taken together, the effect of a mismatch is small for the plane wave and cylindrical wave cases.
Fig 3.
Modulus estimates (first column) and the error in the shear viscosity estimates (second column) are presented for simulated data using the Kelvin-Voigt Maximum Liklihood Estimation (KV-MLE) assuming either cylindrical or plane wave models. The simulation modulus is fixed at 2 kPa while the simulation viscosity is varied from 0.5 to 1.0 Pa·s. Each row contains a different simulation geometry. In the first row, a cylindrical wave geometry is produced by using an Gaussian excitation with a FWHM of 1 mm in both the elevational and lateral directions. In the second row, a plane wave is approximated by setting the FWHM in the elevational direction to 10 cm while the FWHM in the lateral direction is kept at 1 mm. This only approximates plane waves since the grid size is not infinite. In the third row, an intermediate geometry is simulated. For the cylindrical simulation, there is good agreement between the simulated modulus/viscosity and the reconstructed values when a cylindrical wave geometry is assumed. Similarly for the plane simulation, there is good (although not perfect) agreement between the simulated modulus/viscosity and the reconstructed values when a plane wave geometry is assumed. Both assumptions fail for the intermediate geometry. Importantly, the intermediate geometry does not produce an intermediate error in the measurements. Instead, the measurements are markedly biased even at low viscosity.
If the cylindrical and plane wave cases represented the limiting cases for reconstruction/simulation mismatch, then these errors would be tolerable. However, as seen in the last row of Figure 3, the geometrically intermediate case does not yield an intermediate error in the modulus or viscosity estimate. Instead, there is a marked increase in the modulus for all values of viscosity in both plane wave and cylindrical wave based reconstruction cases. There is an initial negative error in the viscosity followed by a gradual increase until the error becomes a positive error. The magnitude of the modulus error is less than 10% throughout the range of viscosities measured. However, the error in the viscosity is as much as 56% of the actual viscosity for the 0.05 Pa·s case and less than 5% for viscosities greater than 0.35 Pa·s.
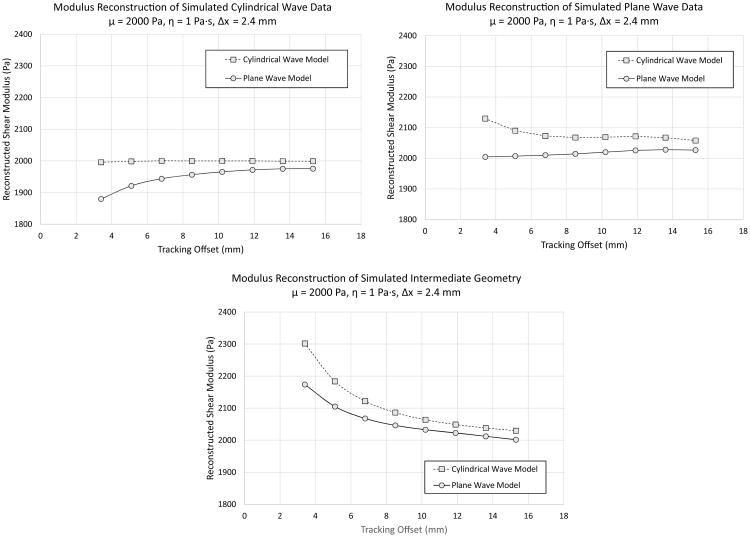
As seen in Figure 2, model mismatch introduces a dependence of the estimate on the tracking offset. In Figure 4, the effect of tracking offset on modulus estimation is demonstrated with respect to the cylindrical, plane, and intermediate excitation geometries. In the cylindrical excitation geometry case, there is good agreement between the simulation modulus and the estimated modulus, using cylindrical wave based reconstruction, at all tracking offsets. The bias introduced when plane waves are assumed in the estimation model is diminished as tracking offset increases. For plane wave simulations, the reciprocal is observed. However, for the intermediate geometry, both plane wave and cylindrical wave based reconstructions yield modulus values that are initially much higher than the simulated modulus but converge to the simulated modulus value as the tracking offset increases.
Fig 4.
The modulus and viscosity is reconstructed using the Kelvin-Voigt Maximum Likelihood Estimator (KV-MLE) for a 2 kPa, 1 Pa·s simulated material with various tracking offsets and excitation geometries. The push beam spacing is fixed at 2.4 mm in all cases. The KV-MLE cylindrical wave and plane wave models are applied to cylindrical wave (upper left panel), plane wave (upper right panel), and an intermediate geometry (lower panel) shear wave simulations. These are the same simulations described in Figure 3. For the cylindrical wave simulation, the cylindrical wave based KV-MLE reconstruction provides the correct modulus regardless of tracking offset. On the other hand, the bias due to plane wave assumption reduces with respect to tracking offset. Similarly, for the plane wave simulation, the plane wave KV-MLE estimate returns a value that is closer to the correct value than the cylindrical wave reconstruction. However, the result is not exact. It is likely that this difference is due to domain size limits. For the intermediate geometry case, both cylindrical and plane wave based estimates substantially overestimate the modulus (an approximately 15% overestimation in the cylindrical case) for the lowest tracking offset. The estimate improves and converges towards the correct solution with increasing tracking offset.
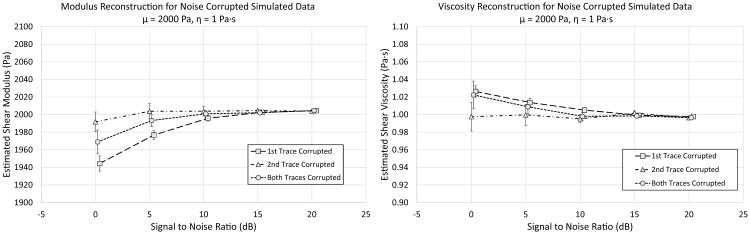
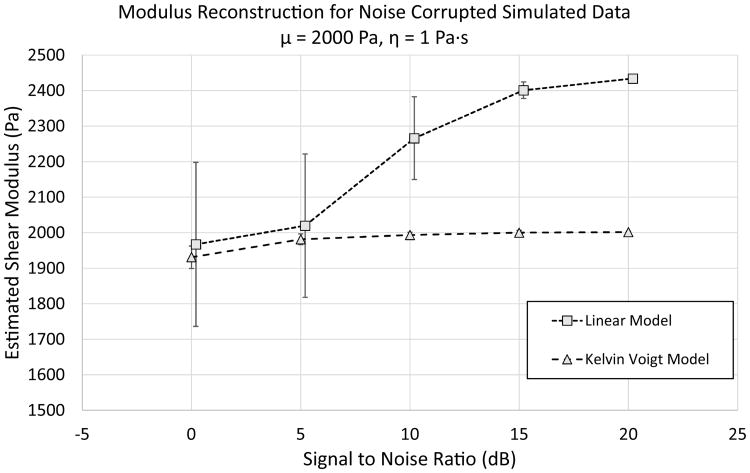
The STL-VE method using the KV-MLE reconstruction assumes that the noise transformed by the wave filter, K, is still Gaussian. The effect of corrupting the wave traces with various amounts the AWGN is demonstrated in Figure 6. Examples of shear wave traces with AWGN yielding SNRs of 20 dB and 0 dB are shown in Figure 5 for reference. In Figure 6, it is seen that corrupting the second trace has no significant effect on the modulus or viscosity estimate, but corrupting the first trace introduces a significant bias in the measurement. Note that this bias is never worse than 3% even for the 0 dB case.
Fig 6.
The effect of AWGN on the STL-VE KV-MLE reconstruction method is demonstrated. AWGN is applied to the shear wave traces prior to KV-MLE reconstruction using a cylindrical wave simulation and a cylindrical wave reconstruction assumption. The reconstructed shear modulus (left) and shear viscosity (right) are reported. The noise is set such that the ratio of the average power of the signal to the average power of the noise is equal to the desired SNR in dB. The area of reconstruction is fixed to 1 mm2. The noise is either added to both traces (Both Traces Corrupted), added twice (different realizations) to the first excitation (1st Trace Corrupted), or added twice to the second excitation (2nd Trace Corrupted). As a result the same total noise is applied in all three cases. The error bars are the 95% confidence intervals for the measurement mean obtained over 20 different realizations of the simulation. It is seen that when the noise is only applied to the second trace there is no significant bias in the data. When the noise is added only to the first trace there is a significant in the modulus (an approximately 5% underestimate). Applying noise to both traces evenly produces an intermediate degree of bias in the modulus(an approximately 2.5% underestimate). A similar trend for shear viscosity with noise causing an overestimation in the measurement.
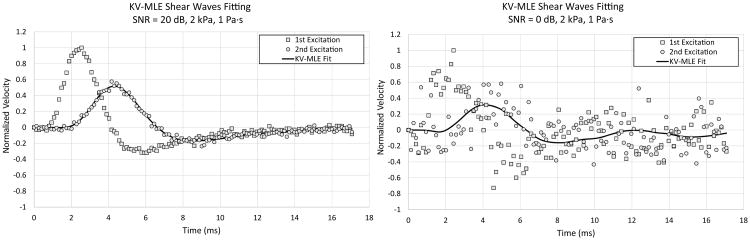
Fig 5.
To test the robustness of the MLE algorithm in the presence of noise, simulated shear wave traces are corrupted with Added White Gaussian Noise (AWGN). On the left, the SNR is set to 20 dB. On the right, the SNR is 0 dB. The underlying signal is identical and generated using a 2 kPa, 1Pa·s simulated material. The excitation is a cylindrically symmetric Gaussian with 1 mm FWHM. The tracking to push offset is 5.1 mm and the push to push spacing is 2.4 mm. The SNR of the right panel is unrealistically low but a fit to the data is achievable for the ROI size utilized.
The precision of the MLE reconstruction depends on the using the correct material model. In Figure 7, the effect of using the wrong elastic model on precision is demonstrated. At high SNR, using the linear model, instead of the simulation matched KV model, simply causes a bias in the measurement. However, the variance of the linear model based reconstruction is demonstrated to be considerably larger than the variance of the KV based model reconstruction.
Fig 7.
The precision of the STL-VE MLE estimate depends on the chosen model. AWGN is applied to the shear wave traces prior to KV-MLE reconstruction and Linear-MLE reconstruction. A cylindrical wave simulation is utilized and a cylindrical wave reconstruction is assumed. The noise is set such that the ratio of the average power of the signal to the average power of the noise is equal to the desired SNR in dB. The area of reconstruction is fixed to 1 mm2. The error bars plotted represent the standard deviation of the reconstruction over 20 different realizations. As observed in Figure 2, using the incorrect (Linear) viscoelastic model induces a measurement bias. When the correct (KV) viscoelastic model is used, a slight bias (70 Pa) is introduced at low SNR as in Figure 6. However, when noise is applied and the incorrect viscoelastic model is used, a considerably larger shift in the mean occurs (466 Pa). Additionally, when compared to the KV case, the Linear case has a much larger standard deviation (31 Pa vs. 230 Pa at 0 SNR). This suggests that the choice of model can have a profound effect on the estimator precision.
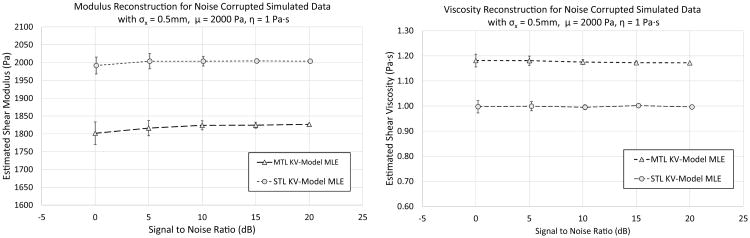
The STL-VE method via the KV-MLE algorithm is optimized for STL not MTL. The results of introducing a tracking location error is demonstrated in Figure 8. A significant bias is introduced when MTL data is processed using the STL-VE KV-MLE algorithm. This bias is seen to be far larger than the bias introduced by low SNR. For this simulated material (2 kPa, 1 Pa·s), MTL yields a 10% underestimate of the modulus and a 18% overestimate of the viscosity.
Fig 8.
The effect of AWGN on the STL-VE KV-MLE reconstruction method in the presence of a tracking bias is demonstrated. A tracking error is introduced with an standard deviation of 0.5 mm. When the same realization of the error is used for both traces this is a Single Tracking Location (STL) model. When a different realization is utilized, the result is a Multiple Tracking Location (MTL) model. The area of reconstruction is fixed to 1 mm2 with separate realizations of the tracking error and noise at each location within the ROI. A total of 20 realizations of the entire simulation are averaged to arrive at the mean and standard deviation of the measurement for each noise level. The error bars represent the standard deviation of the measurement. The modulus (left panel) and viscosity (right panel) are reconstructed for both MTL and STL cases. It is clear that the presence of the tracking error in the MTL data set causes a significant bias in the modulus and viscosity estimates. In this case, there is a 10% underestimate of the modulus and a 20 % overestimate of the viscosity in the MTL case.
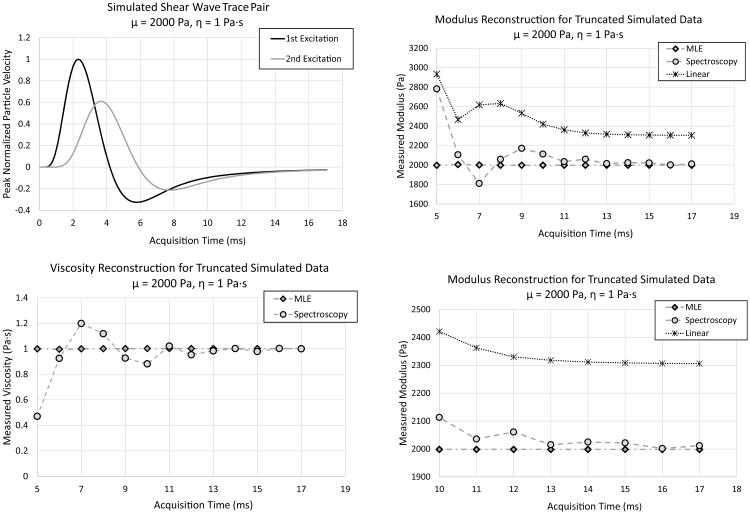
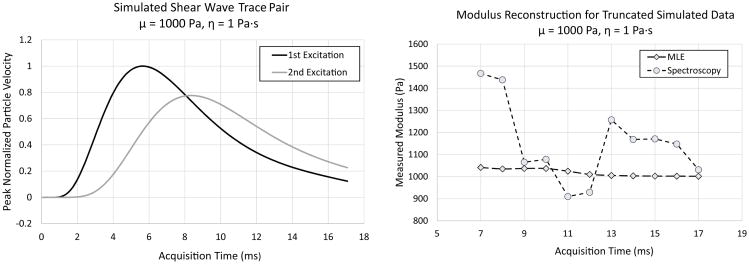
Robustness against signal truncation is a major advantage of using the KV-MLE method for estimating the modulus from STL-VE data when compared to a simple spectroscopic approach. The effect of signal truncation on linear elastic STL-SWEI estimation, as well as STL-VE estimation for both a naive spectroscopic implementation and the KV-MLE method is demonstrated in Figure 9. The example simulation for this study is for a 2 kPa, 1 Pa·s material subject to a cylindrical wave excitation. It is seen that a decrease in the acquisition time leads to a general increase in the linear elastic STL-SWEI estimate. However, it is not a monotonic increase. The accuracy of the spectroscopy method degrades with decreasing acquisition time, failing to reproduce the correct modulus for all times less than 13 ms. On the other hand, the KV-MLE method correctly reproduces that simulated modulus and viscosity at all offsets. A softer 1 kPa, 1 Pa·s material is simulated and presented in Figure 10. In this case, the spectroscopy result never yields the correct modulus. However, the KV-MLE estimate yields a result that is within 5% of the correct modulus value for all acquisition times tested. This is true even at 7 ms when the peak of the second excitation is truncated.
Fig 9.
The change in the estimate produced by linear estimation, spectroscopy, and KV-MLE, due to truncation in the received signal, is investigated for a 2 kPa, 1 Pa·s simulated material. Cylindrical wave simulation is performed with the example shear wave traces in the upper left panel. Truncating this data set at various acquisition times has varying effects on the different estimators. In the upper right, the modulus is measured as a function of the total acquisition time. For linear and spectroscopic estimates, decreasing the acquisition time introduces a unpredictable bias in the measurement. Generally, there is an increase in the measured modulus, but this is not a monotonic trend. The viscosity estimate (lower left panel) is also severely impacted by decreasing acquisition time when spectroscopy is used. The lower right panel, shows a magnified view of modulus estimates for the acquisition time greater than 10 ms. The spectroscopy result approaches the correct value with increasing acquisition time. The KV-MLE estimate returns the correct modulus and viscosity for all acquisition times. Therefore, only the KV-MLE method is robust against signal truncation.
Fig 10.
The change in the estimate produced by linear estimation, spectroscopy, and KV-MLE, due to truncation in the received signal, is investigated for a relatively soft 1 kPa, 1 Pa·s material. Cylindrical wave simulation is performed with the example shear wave traces in the left panel. The modulus as measured by spectroscopy does varies greatly over a range of acquisition time cut-offs (right panel). The KV-MLE estimate does exhibit some bias for acquisition times less than 13 ms. However, this bias is never worse than 5% for the range of cut-offs considered.
B. Liver Study Results
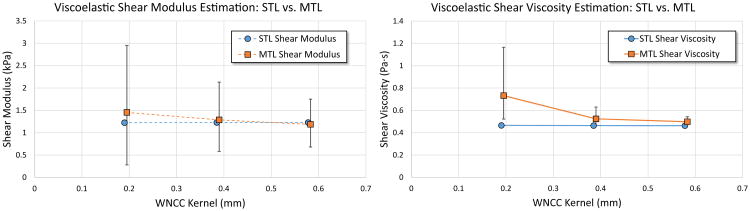
The MLE viscosity estimation method is demonstrated on bovine liver images in Figure 11 for both STL and MTL data. The images are produced by averaging the velocity data from eight separate data acquisitions and calculating the purely elastic modulus by way of cross-correlation. The measured elastic modulus by cross-correlation varies widely across the image (1 - 3 kPa). A region of interest was selected with a relatively homogeneous elastic modulus estimate (1.4 - 1.5 kPa) containing 464 total trace pairs. The coefficient of determination for the fit of the Wave Filter to the ROI is 0.97 ± 0.03 and 0.91 ± 0.08 for the STL and MTL cases, respectively. Considering the size of the ROI, it is evident that the STL method provides significantly better fits than the MTL method. The modulus and the viscosity are measured slightly higher in the MTL case than in the STL case with MTL yielding μ = 1.29 kPa and η = 0.52 Pa·s and STL yielding μ = 1.22 kPa and η = 0.46 Pa·s. The significance of this difference is explored in Figure 12 where the WNCC window size is varied. A larger measurement variability in the MTL case is seen for both the modulus and the viscosity estimate at short WNCC length. The average viscosity measurement is notably higher than that measured for STL at short WNCC window lengths and converges to the STL measurement with increasing WNCC length. This result is consistent with (45).
Fig 11.
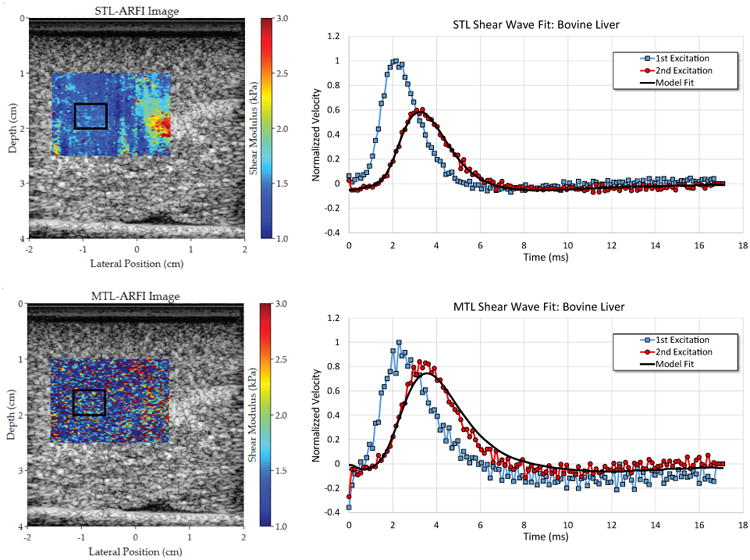
Matched and registered bovine liver images are shown (left column) using the MTL (bottom row) and STL (top row) beam sequences. Example shear wave pairs (right column) are shown from the boxed analysis ROI. The result of applying the calculated Wave Filter to the first shear wave is shown as the “Model Fit” overlaying the second shear wave. The ROI contains 464 total shear wave pairs. Using STL, the MLE method yielded μ = 1.22 kPa and η = 0.46 Pa·s. MLE analysis of the MTL data yielded μ = 1.29 kPa and η = 0.52 Pa·s. The STL fit was found to be significantly better than the MTL case with a coefficients of determination of 0.97 ± 0.03 and 0.91 ± 0.08, respectively. For both MTL and STL the WNCC window length was fixed at 0.96 mm.
Fig 12.
Using the same ROI as in Figure 11, the shear modulus (left) and the shear viscosity (right) is calculated using both STL and MTL beam sequences. The error bars represent the measurement result when considering only the shear wave data associated with the upper half and the lower half of the purely elastic estimates. The error bars for the STL case are too small to be plotted. In all cases, the range for the MTL measurement is larger than the STL measurement. For the shear viscosity estimates, MTL yields a higher apparent viscosity than STL, converging to the STL result as the WNCC window length increases. The STL result is fixed at μ = 1.22 kPa and η = 0.46 Pa·s regardless of WNCC window length.
V. Discussion
A. Geometry Model, Material Model, and Tracking Model all Effect the Viscosity Measurements
Although the ideal viscoelastic material model for liver has not been established, it is seen that choosing the correct material model alone is not enough to correctly determine the material properties from shear wave elastography data. Figure 2 demonstrates that the geometric model of the shear wave excitation is a very important aspect of the measurement process. If the geometric model is not considered, one might conclude that the viscoelastic model is wrong when there is an apparent decrease in the estimate as a function of tracking offset. In most scenarios, the elevational focus of the transducer need not match the lateral focus. Therefore, we might expect intermediate geometries such as that seen in Figure 3. In these cases, tracking at multiple distances from the source leads to geometric errors in the measured phase. That is, in a similar system (such as SDUV) it may appear that the phase change as a function of distance disagrees with the material model when, in fact, the disagreement is with the geometric model. Furthermore, it was demonstrated in Figure 8 that variability in the tracking location introduced in the MTL configurations (most other ultrasound shear wave techniques) also skews the viscoelastic measurement. Therefore, careful analysis of the actual excitation geometry and tracking configuration is needed to make accurate measurements of material viscoelastic properties. One cannot immediately dismiss a material model (such as the KV model) as inadequate for some material without knowing exactly how other assumptions in the estimation model are effecting the measurement.
One metric for accessing the quality of the model may be the goodness of the data fit provided by that model. However, this cannot serve as definitive proof that the model is correct in a physical sense. Consider that in (45) the tracking error behaves as if it is a higher order viscoelastic term. Conceivably, one could define a three parameter model of viscoelasticity that would encapsulate this tracking error induced bias. This may even provide good fits to the underlying data. However, the resulting parameters would not accurately reflect the material's properties. Instead, a property of the imaging system obfuscates the true material properties. To avoid this pitfall, a complete analysis of the estimation process is required as presented here for the STL-VE method.
B. The MLE Algorithm: Noise, Data Truncation, and Performance
The MLE algorithm operates under the assumption that noise sources are all AWGN. It is seen in Figure 6 that even when AWGN is provided, the MLE algorithm is still biased. This is because the Gaussian assumption for the probability density function, (28), is generally invalid. When there is no noise in the first trace of the shear wave trace pair, then (28) is Gaussian. However, as the noise on the first trace increases, the Gaussian approximation become increasingly inaccurate and the MLE becomes biased. While it is not realistic that only one trace would be noise corrupted, this example serves to demonstrate the limitations of the MLE method. Additionally, this data shows that focusing efforts to reduce signal noise (i.e. by averaging over multiple acquisitions) on the first trace, instead of the second trace, would be optimal for reducing bias. In reality, the displacement estimates are likely not zero mean AWGN. Therefore, more complicated biasing of the MLE results are likely when the tracking method is considered. A thorough analysis of how biases and correlations in the displacement estimate effect the MLE estimator is left as future work.
The speckle bias is another important variable in the performance of the MLE. We have demonstrated that using an STL configuration to eliminate this bias vastly improves the MLE accuracy. This is seen in Figures 8 and 12. However, the appearance of the effect differs between the simulated case (Figure 8) and reality (Figure 12). Referring to (40), we hypothesize that this difference is due to correlations between xe1 and xe2. It is required in (46) that xe1 and xe2 be uncorrelated. However, this assumption is likely invalid in the limit of short tracking beam separations where the two probability distributions will be strongly correlated due to overlapping speckle. In fact, in the limiting case of a point target centered between two overlapping tracking beams, xe1 and xe2 are expected to be anticorrelated. While the approximation (46) is probably not valid for real data, the prediction that MTL configurations will bias viscosity estimates was seen experimentally.
Robustness against data truncation is a major advantage to using the MLE method over spectral methods. This was demonstrated in Figures 9 and 10. The argument might be made that this is a trivial feature because longer acquisition times can be readily programmed into any real scanner. However, there are a number of situations where truncating data may be desirable. For example, in small samples, additional shear waves may be generated at the domain edges (mode conversion) and travel at non-zero angles relative to the shear wave of interest. Since the two waves are not traveling in the same direction, they will not appear to have the same wave speed. With two different waves in the temporal field of view, the MLE's behavior is undefined. In this case, truncating the data to only include the waves of interest can be beneficial but depending on the degree of overlap there may not be enough enough data left for an accurate spectrogram to be generated but leaves the MLE unaffected. A similar situation may occur due to reflections at interfaces.
Our focus has been on the precision and accuracy of an MLE based method for fitting viscoelastic models to STL-SWEI data. However, the added complexity of the MLE method does require additional computation time. We previously demonstrated real-time capabilities with regard to speckle tracking and linear elastic image formation with a WNCC processing rate of 5000 frames/s [20]. The results of these first processing steps are passed into the MLE kernel after extracting some ROI. For the ROIs depicted in Figure 11, the time required to perform the MLE estimation on an AMD Radeon R290 GPU is less than 4 seconds. It may be possible to reduce this time with further optimization but this is beyond the scope of this work. As it is implemented here, the MLE estimate can be made at experiment time. This allows for investigators to act on feedback from the MLE in time critical experiments (i.e. clinical and animal studies).
The choice of MTL or STL configuration for the acquisition has no impact on the amount of time needed to perform any of the processing steps. With parallel beamforming, the acquisition part of the MTL experiment could theoretically take half the time of the STL experiment. Since our implementation does not utilize this feature, there is no actual temporal performance difference between the two methods. It is also important to note that the two shear wave traces in each trace pair are acquired consecutively with no intervening acquisitions. As a result, the impact of physiological motions with periods longer than twice the trace length (typically 20 ms) are minimized. Considering the minimal temporal performance impact and the improved accuracy, the authors believe that STL configuration should be preferred over the MTL configuration for ARFI based viscosity estimation.
C. Model Appropriateness for Liver Imaging
It was demonstrated that the combination of a cylindrical wave geometry model and a Kelvin-Voigt material model achieved reasonably good fits to the shear wave data for bovine livers in Figure 11. On the other hand, only one set of tracking/pushing offsets were used for this analysis. As we have shown, variation in the estimate with changing imaging parameters is a hallmark of a poor model fit. Therefore, the work presented here cannot affirm the appropriateness of the KV model for liver estimation. Analyzing the variability of the measurement with tracking/pushing offsets is left as future work. Finally, the effect of inhomogeneity on the material estimates has not been explored here. For materials with focal inhomogeneities, we might expect that diffraction of the shear wave front will produce an additional source of error. Nominally, this error would be dependent on the tracking offset since the degree of divergence between a wave that has been diffracted and one that has not is distance dependent. In the bovine liver images presented in Figure 11, there is a evidence of inhomogeneities in the image. An ROI from a region with relatively low variance was chosen for analysis. It is not clear how regional variability might impact the MLE's performance. However, it can be seen in the MTL image that the tissue variability, which was apparent in the STL image, is no longer visible. This suggests that the measurement variability introduced by MTL is at least on the order of the tissue variability of this sample. Further, if we also consider Figure 12, STL appears to be much more precise than MTL. It is not clear how this translates to clinical liver measurements and further studies will be required to determine this.
As discussed above, the MLE method produces biased results when the MTL tracking configuration is used, when the geometry of the excitation is mis-represented, and when the wrong viscoelastic material model is chosen. However, correcting for these biases does not necessarily improve the clinical utility. It is conceivable that if a standard set of probes, push beam geometries, and tracking settings are used, then these biases can be fixed to a constant value. Still, it should be noted that these biases as presented in Figure 3 are not linear and the degree of the bias is effected by noise (Figure 7). What is more concerning is the effect of model selection on precision as demonstrated in Figure 7. The low SNR standard deviation of the linear elastic model was found to be 230 Pa in this experiment. This is approximately 11% of the mean measurement. At this level of variability, it is conceivable that fibrosis stage may be mis-characterized. Consider that in [5] the F2-F3 patients had a mean elasticity of 2.56 kPa and the F0-F1 patients had a mean elasticity of 2.24 kPa. In this case, the F0-F1 patients have livers that are only 13% less stiff than the F2-F3 patients. This difference is only slightly greater than our measurement variance in the linear estimation case. To improve the precision, two options exist: increase the SNR or choose a better model. While SNR can be improved with larger ROIs this leads to spatial averaging that limits one's ability to detect tissue variation. Alternatively, increasing the number of acquisitions can improve SNR but is limited by physiological motion. Finding a better model is an ideal solution since it allows for fewer acquisitions and smaller ROIs to achieve the same estimate variance.
VI. Conclusions and Future Work
A new viscoelastographic technique known as STL-VE has been introduced. The method was rigorously developed from the underlying physical model and application of estimation theory and was implemented as a GPU accelerated software package providing massive parallel processing. Simulations demonstrated accurate modulus reconstruction using the STL-VE method when excitation geometry is matched to that assumed in the model. The effect of geometry mismatch and changing imaging parameters, such as the tracking offset, was characterized. Additionally, we showed the effect of noise and signal truncation on the performance of STL-VE. In ex-vivo experiments, good agreement between the STL-VE MLE model and the shear wave data produced through the imaging of bovine liver was observed. Finally, the critical role of imaging using the STL beam sequence rather than the MTL beam sequence for viscosity estimation was demonstrated. In our future work, we will examine the possibility of staging liver fibrosis using STL-VE both in tissue and in matched simulations. Matched simulations will allow us to determine how biases introduced by geometric and material model uncertainty might effect fibrosis stage cut-off. Additionally, the effects of inhomogeneity and non-Gaussian noise sources will be investigated. Finally, the utility of alternative viscoelastic models in the STL-VE reconstruction algorithm will be investigated.
Acknowledgments
The authors gratefully acknowledge the support of the NIH (R03 EB016127).
References
- 1.Yeh WC, Li PC, Jeng YM, Hsu HC, Kuo PL, Li ML, Yang PM, Lee PH. Elastic modulus measurements of human liver and correlation with pathology. Ultrasound Med Biol. 2002;28(4):467–74. doi: 10.1016/s0301-5629(02)00489-1. [DOI] [PubMed] [Google Scholar]
- 2.Piscaglia F, Marinelli S, Bota S, Serra C, Venerandi L, Leoni S, Salvatore V. The role of ultrasound elastographic techniques in chronic liver disease: Current status and future perspectives. Eur J Radiol. 2013 doi: 10.1016/j.ejrad.2013.06.009. [DOI] [PubMed] [Google Scholar]
- 3.Salameh N, Peeters F, Sinkus R, Abarca-Quinones J, Annet L, Ter Beek LC, Leclercq I, Van Beers BE. Hepatic viscoelastic parameters measured with mr elastography: correlations with quantitative analysis of liver fibrosis in the rat. J Magn Reson Imaging. 2007;26(4):956–62. doi: 10.1002/jmri.21099. [DOI] [PubMed] [Google Scholar]
- 4.Chen SG, Sanchez W, Callstrom MR, Gorman B, Lewis JT, Sanderson SO, Greenleaf JF, Xie H, Shi Y, Pashley M, Shamdasani V, Lachman M, Metz S. Assessment of liver viscoelasticity by using shear waves induced by ultrasound radiation force. Radiology. 2013;266(3):964–970. doi: 10.1148/radiol.12120837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Huwart L, Peeters F, Sinkus R, Annet L, Salameh N, ter Beek LC, Horsmans Y, Van Beers BE. Liver fibrosis: non-invasive assessment with mr elastography. NMR Biomed. 2006;19(2):173–9. doi: 10.1002/nbm.1030. [DOI] [PubMed] [Google Scholar]
- 6.Orescanin M, Insana M. Shear modulus estimation with vibrating needle stimulation. IEEE Trans Ultrason Ferroelectr Freq Control. 2010;57(6):1358–67. doi: 10.1109/TUFFC.2010.1555. [DOI] [PubMed] [Google Scholar]
- 7.Chen S, Urban MW, Pislaru C, Kinnick R, Zheng Y, Yao A, Greenleaf JF. Shearwave dispersion ultrasound vibrometry (sduv) for measuring tissue elasticity and viscosity. IEEE Trans Ultrason Ferroelectr Freq Control. 2009;56(1):55–62. doi: 10.1109/TUFFC.2009.1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hoyt K, Kneezel T, Castaneda B, Parker KJ. Quantitative sonoelastography for the in vivo assessment of skeletal muscle viscoelasticity. Phys Med Biol. 2008;53(15):4063–80. doi: 10.1088/0031-9155/53/15/004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Amador C, Urban MW, Chen S, Greenleaf JF. Loss tangent and complex modulus estimated by acoustic radiation force creep and shear wave dispersion. Phys Med Biol. 2012;57(5):1263–82. doi: 10.1088/0031-9155/57/5/1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Scola MR, Baggesen LM, Gallippi CM. Multi-push (mp) acoustic radiation force (arf) ultrasound for assessing tissue viscoelasticity, in vivo. Conf Proc IEEE Eng Med Biol Soc. 2012;2012:2323–6. doi: 10.1109/EMBC.2012.6346428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bercoff J, Tanter M, Muller M, Fink M. The role of viscosity in the impulse diffraction field of elastic waves induced by the acoustic radiation force. IEEE Trans Ultrason Ferroelectr Freq Control. 2004;51(11):1523–36. doi: 10.1109/tuffc.2004.1367494. [DOI] [PubMed] [Google Scholar]
- 12.McAleavey SA, Menon M, Orszulak J. Shear-modulus estimation by application of spatially-modulated impulsive acoustic radiation force. Ultrason Imaging. 2007;29(2):87–104. doi: 10.1177/016173460702900202. [DOI] [PubMed] [Google Scholar]
- 13.Elegbe EC, McAleavey SA. Single tracking location methods suppress speckle noise in shear wave velocity estimation. Ultrason Imaging. 2013;35(2):109–25. doi: 10.1177/0161734612474159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mainardi F. Fractional calculus and waves in linear viscoelasticity : an introduction to mathematical models. London; Hackensack, NJ: Imperial College Press; 2010. [Google Scholar]
- 15.Kay SM. Fundamentals of statistical signal processing, ser Prentice Hall signal processing series. Englewood Cliffs, N.J.: Prentice-Hall PTR; 1993. [Google Scholar]
- 16.McAleavey S, Langdon J, Osapoetra L. Shear wave arrival time estimates correlate with local speckle pattern. Ultrasonics Symposium (IUS), 2014 IEEE International. :643–646. doi: 10.1109/TUFFC.2015.007171. Conference Proceedings. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bjorck A. Numerical methods for least squares problems. Philadelphia: SIAM; 1996. [Google Scholar]
- 18.Orescanin M, Wang Y, Insana M. 3-d fdtd simulation of shear waves for evaluation of complex modulus imaging. IEEE Trans Ultrason Ferroelectr Freq Control. 2011;58(2):389–98. doi: 10.1109/TUFFC.2011.1816. [DOI] [PubMed] [Google Scholar]
- 19.Berenger JP. A perfectly matched layer for the absorption of electromagnetic-waves. Journal of Computational Physics. 1994;114(2):185–200. [Google Scholar]
- 20.Langdon JH, McAleavey SA. Real-time single track location ultrasound elasticity imaging using graphic processing units. Image and Signal Processing Workshop (WNYISPW), 2014 IEEE Western New York. :42–46. Conference Proceedings. [Google Scholar]