Conformational dynamics of non-synonymous variants at protein interfaces reveals disease association

Abstract

Recent studies have shown that the protein interface sites between individual monomeric units in biological assemblies are enriched in disease-associated non-synonymous single nucleotide variants (nsSNVs). In order to elucidate the mechanistic underpinning of this observation, we investigated the conformational dynamic properties of protein interface sites through a site-specific structural dynamic flexibility metric (dfi) for 333 multimeric protein assemblies. dfi measures the dynamic resilience of a single residue to perturbations that occurred in the rest of the protein structure and identifies sites contributing the most to functionally critical dynamics. Analysis of dfi profiles of over a thousand positions harboring variation revealed that amino acid residues at interfaces have lower average dfi (31%) than those present at non-interfaces (50%), which means that protein interfaces have less dynamic flexibility. Interestingly, interface sites with disease-associated nsSNVs have significantly lower average dfi (23%) as compared to those of neutral nsSNVs (42%), which directly relates structural dynamics to functional importance. We found that less conserved interface positions show much lower dfi for disease nsSNVs as compared to neutral nsSNVs. In this case, dfi is better as compared to the accessible surface area metric, which is based on the static protein structure. Overall, our proteome-wide conformational dynamics analysis indicates that certain interface sites play a critical role in functionally related dynamics (i.e., those with low dfi values), therefore mutations at those sites are more likely to be associated with disease.

INTRODUCTION

Advances in sequencing technologies are providing a wealth of data on human genetic variation. It is now clear that any personal exome contains thousands of variants, the majority of which are non-synonymous single nucleotide variants (nsSNVs) (1). However, distinguishing between neutral variants (i.e., those with little or no effect on phenotype) from variants associated with disease still remains a major challenge for both monogenic (Mendelian) and complex diseases (1, 2). The current state-of-the-art methods for diagnosing amino acid variants primarily employ evolutionary information obtained from multispecies sequence analysis in a variety of ways (1–6). While these methods have been used extensively, they often fail to correctly diagnose damaging variants at evolutionarily variable positions and neutral variants at highly conserved positions (2).

Several methods have been proposed to incorporate structure-based information from protein structures. Two prominent methods are to use accessible surface area (ASA), which determines the surface area of a protein accessible to a solvent, and the change in protein stability, which utilizes the difference in free energy between the folded and unfolded state upon mutation through empirical calculation based on the 3-D structure (7–12). Interestingly, the addition of these modalities has only produced a marginal 3–4% improvement in the rate of true positive diagnosis (9, 13, 14). A common feature among these methods is that they are based on the static 3-D structure of the protein, which fails to capture the dynamic motion of the protein structure. From the conformational transitions of allosteric proteins to the required flexibility of a ligand-binding site, proteins must fluctuate to achieve their function (15–30).

A reason for the lack of methods incorporating protein dynamics into nsSNV diagnoses could be the absence of amino acid site-specific measures that can statistically quantify the contribution and impact of each position on the conformational dynamics of the protein in a fast and efficient way. We recently developed a dynamic flexibility index (dfi), which measures the contribution of each position to functionally important dynamics (31). Through dfi analyses of more than 100 monomeric proteins, we found that the added feature of protein dynamics has the potential to distinguish between nsSNVs that impact biological function and those that have no effect on function (neutral nsSNVs) at a proteome scale (31). Moreover, this large-scale analysis including population variations implicated in diseases, functionally critical positions (catalytic and binding sites), and evolutionary rates of substitutions produced concordant patterns; it established that the preservation of dynamic properties of residues in a protein structure is critical for maintaining the protein/biological function (31).

The dfi metric has not yet been evaluated for biological assemblies. Many proteins form biological assemblies in order to perform their specific functions in the cell. Recent studies have shown that nsSNVs located at protein-protein interface sites are often associated with disease (10, 32) where additional metrics beyond evolutionary information can be useful (33). Therefore, we report the dfi analysis for proteins that form biological assemblies and its relationship with evolutionary conservation. We also compare the difference between the dfi of disease-associated and neutral nsSNVs when it is calculated in biological assemblies and when it is calculated by using proteins as monomers in order to determine which is more informative at phenotypic prediction. Moreover, we compare dfi with the static measure of solvent accessible area, which has also been used to predict disease-associated nsSNVs in biological assemblies (10).

METHODS

Data set

We generated a curated dataset of 1,174 protein nsSNVs using available databases, including HumVar that contains 301 disease-associated and 200 neutral population variants compiled for PolyPhen-2 (6), 383 neutral variants from the 1000 Genomes Project with those having population frequency greater than 10% (34), and 290 disease-associated variants from the Human Gene Mutation Database (HGMD) (35). The set of 333 unique multimeric proteins containing 591 disease-associated and 583 neutral nsSNVs was modeled such that all the proteins formed assemblies and have 3-D structures in the Protein Data Bank (36) with >80% sequence identity between the reference sequence and experimentally-derived protein structures and >80% sequence coverage using BLAST. The high constraints were imposed to ensure that the structures used in this study are real experimental human proteins rather than pure homology models.

The dfi metric for biological assemblies

The dynamic flexibility index (dfi) is a metric to determine the structural flexibility at specific sites on a protein. We applied our original method (31) directly to biological assemblies (BAs) such that the dynamic flexibility for each position in the BA is considered. In brief, the method is based on the perturbation response scanning (PRS) method where the equilibrium structure of a protein is constructed as a 3-D elastic network model (ENM) in which the nodes are represented by C-alpha atoms (37, 38), and the pairwise potential between each atom is given by the potential of a harmonic spring. A small perturbation in form of random Brownian kick is applied sequentially to each C-alpha atom in the elastic network. The perturbation on a single residue results in a cascade of perturbations to all other atoms in the network, thus inducing a global response. The fluctuation response profile of the positions upon perturbation of a single residue ([�Δ_3N×1) is obtained using linear response theory and given by the equation

$${\left[\mathbf{\Delta }\mathbf{R}\right]}_{3N\times 1}={\left({\left[\mathbf{H}\right]}_{3N\times 3N}\right)}^{-1}{\left[\mathbf{\Delta }\mathbf{F}\right]}_{3N\times 1}$$

where the ΔF vector contains the components of the externally applied random unit force vectors ( $\widehat{f}$) on the selected residues, and H⁻¹ is the inverse of Hessian matrix (i.e. H, the Hessian, is a 3N×3N matrix composed of the second order derivatives of the harmonic potential with respect to the components of the position vectors for the chain of length N). To minimize the effects of randomness, this perturbation procedure is performed ten times to ensure that the applied force is isotropic with a zero angular average ( $‹\widehat{f}›=0$), and the response vector ΔRⁱ_j is averaged.

In short, the application of the random Brownian kick to a given residue on the 3-D elastic network perturbs the residue interaction network of the protein beyond fluctuations inherent in the system at equilibrium and elicits responses from all other residues in the structure. Through the perturbation response scanning method (PRS) (39, 40), we compute the fluctuation response of residue j, ΔRⁱ_j, both in direction and magnitude upon perturbation. We repeat this perturbation on each single residue for all positions in chain and obtain the response profiles of all other positions. The dynamic flexibility index, dfi, is then obtained by the equation

$$\mathit{dfi}=\frac{{{\displaystyle \sum }}_{i=1}^N{\left|\mathrm{\Delta }{R}^i\right|}_j}{{{\displaystyle \sum }}_{j=1}^N{{\displaystyle \sum }}_{i=1}^N{\left|\mathrm{\Delta }{R}^i\right|}_j}$$

where ${\left|\mathrm{\Delta }{R}^i\right|}_j=\sqrt{‹\mathrm{\Delta }{R}^2›}$ is the magnitude of positional displacements for residue j in response to a perturbation at residue i after averaging out the response vector ΔRⁱ_j over ten different random directional unit forces, and N is the total number of positions on the biological assembly. Note that we compared the dfi values obtained from the coarse-grained ENM model with those obtained from all-atom replica exchange molecular dynamics simulations for several proteins in our earlier work (31) in which the dfi values obtained from these two different simulation approaches yield very high correlations, as Pearson correlation coefficients between PRS and all-atom MD ranged from 0.64 to 0.88 for 5 proteins.

For the monomeric analysis of biological assemblies, the dfi value is estimated using the monomeric unit alone (i.e., for a homomeric dimer with two units of 2N residues only the N residue position of the monomeric unit is considered). Thus, the impact of the interactions aroused due the interaction of interface residues between each unit in the BA is not considered. In estimating the dfi values for the BA, however, the whole complex (i.e., 2N residue positions of the two homomeric units) is used such that the interactions between the interface positions in the BA are explicitly included in the Hessian. Moreover, the flexibility response of residue i on unit 1 after perturbing residue j on unit 2 is computed and included in the dfi profile of unit 1. A workflow depicting the methodology for the dfi analysis of the BA and monomeric unit is provided in Fig. 1.

FIGURE 1.

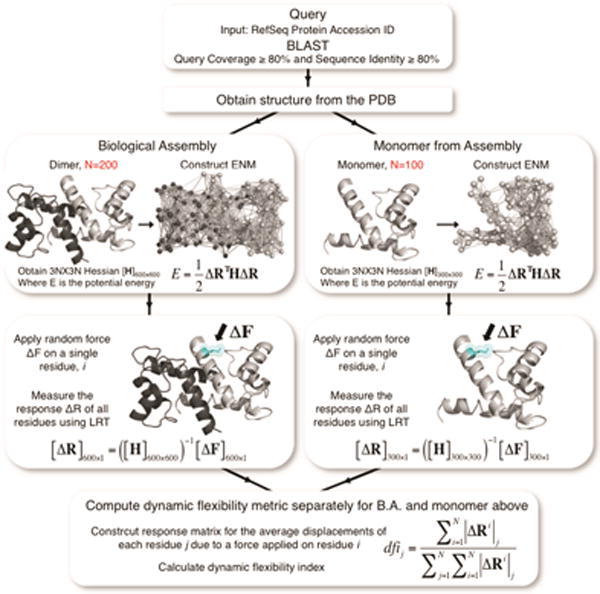
The schematic diagram of the method followed for structural dynamics analysis of each multimeric protein. We identify a three-dimensional (3-D) structure for each protein sequence through a BLAST search using protein data bank (PDB). In this search, the sequence coverage and the sequence identity between the reference sequence query and the known protein structures is set to >80% and >80%, respectively. The identified 3-D experimental structures from PDB are then used for the Perturbation Response Scanning (PRS) model to predict the dynamic flexibility index (%dfi) for each residue position.

Since we collectively analyze atomic positions for a wide variety of protein structures, dfi must be normalized. Thus, the dfi value of a specific atomic position in the protein is expressed as %dfi, which is a percentile rank of that atom in a sorted array of all dfi values in a given protein. The dfi calculation is performed on each biological assembly, which is comprised of two or more chains. The calculation is then done on a single chain taken from the biological assembly (Fig. 1).

Accessible surface area (ASA)

We compare the dfi metric with a static metric known as accessible surface area (ASA) and its capability to quantify phenotypes of nsSNVs. The ASA metric determines the amount of surface area in the crystal that is accessible (i.e. exposed to a solvent). We calculated ASA by using the DSSP program (41). Following the dfi procedure, we normalized ASA values for each residue position and expressed them as %ASA.

Prediction of interface sites

The prediction of molecular interface residues of BAs were determined using the PISA server (42–44). PISA is a computational tool that predicts the strength of interaction between two monomers and the interfaces between them, resulting in the multimer that is likely the functional form of the BA.

Evolutionary Rates

We estimate the absolute evolutionary rate at each site by using a previously described method (2), which computes the number of amino acid substitutions in a given phylogeny following the parsimony algorithm for each site independently (45). The evolutionary rate of amino acid changes across species is then the number of amino acid substitutions divided by the total time elapsed in the tree. Evolutionary rates are in the units of substitutions per amino acid per billion years (Byrs) and are based on protein sequence alignments of 46 species available from the University of California-Santa Cruz resource (UCSC Human Genome Browser) (46).

RESULTS AND DISCUSSION

To assess the effect of using biological assemblies (BAs) on the estimation of conformational dynamic parameters, we compared the dfi values of all 1,174 nsSNVs in 333 BAs with those obtained by using only the monomeric units. Many sites harboring sequence variants showed large differences in %dfi calculated from the BA and monomeric forms (Fig. 2A). For example, many high %dfi sites in the monomeric calculations show rather low %dfi in the BA calculation. We found many of these residues to be located at interface sites in the BA, which seems reasonable since residues at interfaces exhibit a different fluctuation profile in assemblies. This is due to their interaction with the residues of another unit, unlike the monomeric forms where the same residues would interact with a solvent instead. When considering only the interface sites (357 of 1,174), we observe a large difference (p < 0.0001) in the cumulative %dfi distributions (Fig. 2B) between the monomeric and multimeric forms with an average %dfi of 31% for the BA unit and 51% for the monomeric unit. The interface variants had lower dynamic flexibility, with over 50% showing %dfi ≤ 25%. This tendency is expected since the interactions with other monomeric units in the BA lead to a decrease in flexibility. On the other hand, the cumulative %dfi distributions of monomeric and BA units are very similar for the nsSNVs at non-interface sites (817 of 1,174), as shown in Fig. 2C. For these sites, the average %dfi for BA units was 50% and that for their monomeric units was 46%.

FIGURE 2.

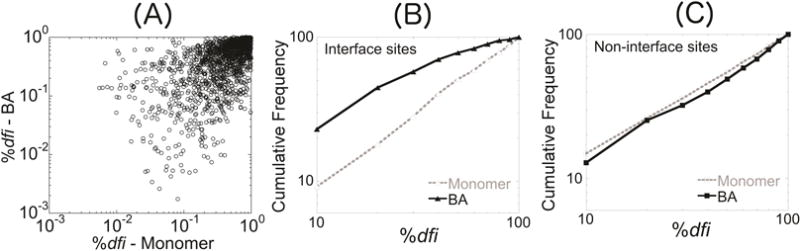
A scatter plot is shown in (A) of the %dfi values for all variants, disease-associated and neutral, using the biological assembly units (y-axis) their corresponding monomeric units (x-axis). Each axis is scaled logarithmically. Many sites exhibit low dfi in the BA but much higher dfi in their monomers, indicating that they are located at interfaces. Cumulative %dfi distributions of interface sites (B) and non-interface sites (C) for the BA units and their corresponding monomeric units.

The above pattern prompted us to investigate whether considering the structural dynamics of the BA is more powerful in distinguishing disease-associated nsSNVs. We computed the cumulative distributions of 207 disease-associated nsSNVs from 62 proteins and 150 neutral nsSNVs from 71 proteins separately for interface sites (Fig. 3). There is a distinct separation between the two cumulative distributions. At lower dfi, the separation of the two curves was pronounced, indicating that sites containing disease-associated variants have lower dfi than those containing neutral variants at interfaces. The average %dfi for disease-associated variants at interfaces is 23% while that for neutral variants is 42% (p < 0.0001).

FIGURE 3.

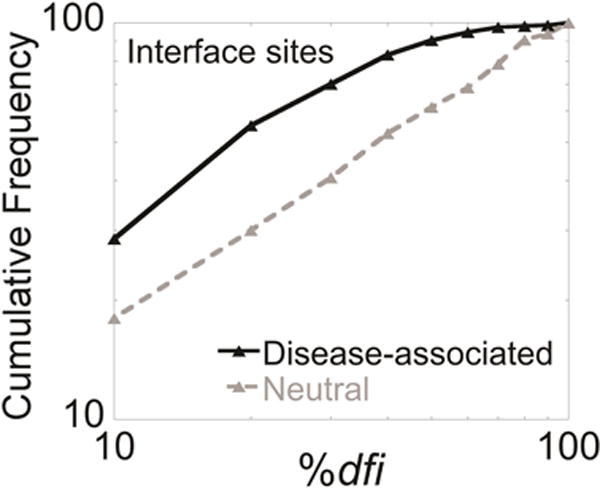
Cumulative %dfi distributions of protein interface sites for disease-associated variants (black line) and neutral variants (grey line) from the human population (compiled from HumVar and the 1000 genomes project). The average %dfi for disease-associated variants at interfaces is 23% while that for neutral variants is 42% (p < 0.0001).

We chose two case studies to shed light on the mechanistic differences for the analysis of individual proteins and BAs. Human pyridoxine-5′-phosphate oxidase (1NRG in the Protein Data Bank) is a homodimer that serves as an important enzyme to catalyze reactions in the vitamin B6 metabolism pathway. Two variants with known disease implications from HGMD were mapped onto the protein interface, as shown in Fig. 4A. The structure is colored within a spectrum of red–yellow–green–cyan–blue, where red shows the highest and blue the lowest values of %dfi. Based on Fig. 4A, it is clear that these two variants located at the interface have low dynamic flexibility (ARG-95 and ARG-229 have a %dfi of 0.07981 and 0.15962 respectively). With such low dfi values those sites are likely critical for function, thus a mutation there will likely lead to a disruption in function. For instance, the site ARG-229 is mutated to TRP-229, which results in the potentially fatal disease, neonatal epileptic encephalopathy (NEE) (35, 47). For the second case, three neutral variants from the 1000 Genomes Project were mapped to the model structure of human carboxypeptidase A1 (homologous structure is 1PYT in the Protein Data Bank) with TYR-435 occurring at an interface site and the other two at non-interface sites (Fig. 4B). From Fig. 4B, it can be seen that these sites have noticeably higher dynamic flexibility. Interestingly, even TYR-435 had a high dfi score of 0.62084 despite its location at an interface. It is expected that interface sites generally have lower dfi values since they are interacting with residues of another protein, thus high dfi at an interface is surprising and could lend useful information relating to the phenotype. Fig. 4 shows how variants within an individual protein could lead to the general trend seen in Fig. 3, which is based on the analysis of more than 100 proteins. Moreover, the trend exhibited in Fig. 3 and the case study presented in Fig. 4 together gives further indication to the notion that dfi may discriminate disease-associated from neutral variants.

FIGURE 4.

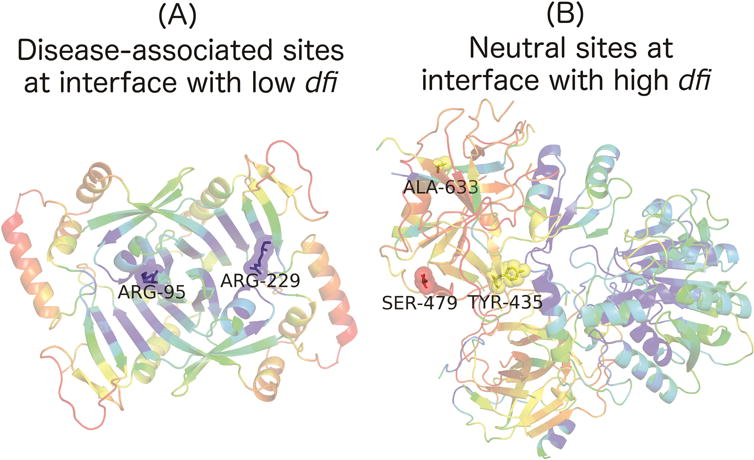
The ribbon diagrams of (A) recombinant human pyridoxine-5′-phosphate oxidase (PDB code: 1NRG) and (B) human carboxypeptidase A1 (PDB code: 1PYT) with respect to dynamic flexibility index, %dfi, are shown. Each structure is colored within a spectrum of red–yellow–green–cyan–blue, where red shows the highest and blue the lowest values of %dfi. In (A), two disease-associated variants are shown, which both occur at interface sites, while (B) shows three neutral variants, with TYR-435 occurring at an interface site and the other two at non-interface sites. The colors of their sticks and spheres correspond to their %dfi.

For comparison, we also examined the performance of ASA, a metric based on the static form of the protein structure, which has also been utilized to differentiate disease-associated nsSNVs from neutral variants (10, 33, 48). We found that the average %ASA showed only a small difference (45% for disease-associated and 66% for neutral population variants), as compared to a 2.5 times difference observed for average %dfi (21% for disease associated and 54% for neutral population variants). We found that there is a correlation between ASA and dfi, as sites with low ASA that are surrounded with other residues rather than solvent would exhibit fewer fluctuations and cause lower dfi values. However, among these low ASA positions, certain positions can be more dynamically critical in translating or controlling the functionally related motion than others due to their residue interaction pattern within the protein structure. By utilizing dfi, we are able to capture these dynamically critical positions. Thus, the above result suggests that the interface residues that play an important role in the collective motion of the BA are more susceptible to damaging mutations.

We examine whether the predictive capabilities of dfi for the BA go beyond that afforded by evolutionary conservation of positions involved by estimating the evolutionary rate (r) for each nsSNV site (as described in the methods section). We divided the estimated evolutionary rate (r) into two different categories: ultra-conserved (r = 0) or less-conserved (r > 0). In our analysis, 37% of interface sites and 30% non-interface sites were ultra-conserved sites. Likewise, 63% of interface sites and 70% of non-interface sites were less-conserved sites. This difference in evolutionary rates is rather small, as compared to conformational dynamics where a higher fraction of interface sites have very low dfi (53% of interface sites and 29% non-interface have dfi ≤ 25%). This prompted us to consider the phenotypic prediction of nsSNVs at interface sites, as the ability to correctly identify disease associated variation at less-conserved sites is not high for many evolutionary rate based in silico prediction tools (1, 2) and many interface sites are at less conserved positions. We surmised that dfi calculated using BAs may provide information beyond that afforded by evolutionary conservation at those sites. Thus, we explored the ability of dfi to discriminate disease-associated and neutral nsSNVs at less-conserved sites (r > 0).

We compared box plots of %dfi and %ASA for disease-associated and neutral variants at interface sites that were less-conserved (Fig. 5A). Remarkably, the average %dfi of disease-associated nsSNVs is approximately 2.5 times lower than that of neutral nsSNVs gathered from human population statistics (6). The average %dfi for disease-associated variants was 25% at less-conserved sites at interfaces, whereas the average %dfi for neutral variants from the 1000 Genomes Project and HumVar was 45% (p < 0.001 when comparing both datasets). This suggests that dfi is likely a useful metric for predicting phenotypes of nsSNVs at less-conserved sites. In comparison, we did not see a suggestive difference in ASA between neutral and disease-associated variants, as the average %ASA for disease-associated sites was 47% at less-conserved interface sites, whereas the average %ASA for neutral sites was 52% (p = 0.63 for disease vs. 1000 Genomes Project and HumVar). We then conducted a receiver operating characteristics (ROC) curve analysis for %dfi and %ASA to elucidate their ability to distinguish between disease and neutral phenotypes of nsSNVs. A randomly generated test set consisting of 10% of the entire data set (which only includes nsSNVs at interfaces) was used and the remaining 90% was used for training (4, 49). The area under the curve (AUC) for dfi is 0.71 and 0.56 for ASA (Fig. 5B). Therefore, the use of dfi appears to be advantageous for use in future diagnostic methods.

FIGURE 5.

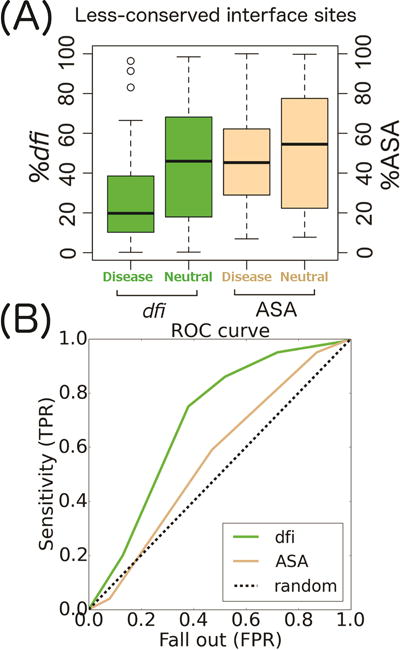
A) A box plot of %dfi (green) and %ASA (brown) distributions comparing disease-associated and neutral nsSNVs for less-conserved variants (evolutionary rate r > 0) occurring at protein interfaces. Box plots show median, upper, and lower quartiles, and whiskers represent maximum and minimum values. (B) A receiver operating characteristics (ROC) curve for dfi and ASA using a test set that was generated from 10% of the whole data set. The area under the curve (AUC) for dfi and ASA was 0.71 and 0.56 respectively. TPR and FPR are true and false positive rates in predicting disease associated nsSNVs to be identified as non-neutral, respectively.

CONCLUSION

This work has provided evidence that non-synonymous variants observed at protein interface sites with low dfi are more likely to be disease-associated. This may be due to the fact that protein interface sites with low dfi play a critical role in modulating the functionally important inter-dynamics of biological assemblies. Indeed, evolutionary based metrics as well as proteins’ static structure based metrics such as ASA have unique strengths in predicting the phenotypic impact, thus incorporating metrics based on structural dynamics (such as dfi) along with other metrics may increase the prediction accuracy of phenotypes of interface nsSNVs.