Cortical instability drives periodic supracellular actin pattern formation in epithelial tubes

Significance

Robust pattern formation is a ubiquitous question of developmental biology. In 1952, Turing proposed in a seminal paper that this could be achieved by a hydrodynamical instability of two diffusing species reacting with each other, but direct experimental evidence of how a mechanism is implemented biologically is still lacking. In this paper, we show by a combination of experiment and theory that the actin cytoskeleton, one of the main force-producing mechanisms in biology, has the property to self-organize into regular supracellular patterns in vivo in Drosophila. We show that the wavelength of the pattern depends on the physical properties of the gel and can be modified experimentally.

Abstract

An essential question of morphogenesis is how patterns arise without preexisting positional information, as inspired by Turing. In the past few years, cytoskeletal flows in the cell cortex have been identified as a key mechanism of molecular patterning at the subcellular level. Theoretical and in vitro studies have suggested that biological polymers such as actomyosin gels have the property to self-organize, but the applicability of this concept in an in vivo setting remains unclear. Here, we report that the regular spacing pattern of supracellular actin rings in the Drosophila tracheal tubule is governed by a self-organizing principle. We propose a simple biophysical model where pattern formation arises from the interplay of myosin contractility and actin turnover. We validate the hypotheses of the model using photobleaching experiments and report that the formation of actin rings is contractility dependent. Moreover, genetic and pharmacological perturbations of the physical properties of the actomyosin gel modify the spacing of the pattern, as the model predicted. In addition, our model posited a role of cortical friction in stabilizing the spacing pattern of actin rings. Consistently, genetic depletion of apical extracellular matrix caused strikingly dynamic movements of actin rings, mirroring our model prediction of a transition from steady to chaotic actin patterns at low cortical friction. Our results therefore demonstrate quantitatively that a hydrodynamical instability of the actin cortex can trigger regular pattern formation and drive morphogenesis in an in vivo setting.

Self-organization is one of the principal mechanisms of biological pattern formation at the molecular, cellular, and tissue scale. Although the pioneering work of Turing (1) has suggested reaction–diffusion as a generic route toward pattern generation (2), a concrete biomolecular or mechanical understanding of how this might occur in vivo remains elusive, except in a few specific cases (3–5). For instance, Kondo and coworkers (6) demonstrated that pigment patterning on the skin of the Pomocanthus imperator can be understood quantitatively from the simple attraction–repulsion kinetics of two cell types.

At the cellular level, active structures, such as the cytoskeleton, are generically expected to display a large variety of structures from a theoretical perspective (7–12), many of which have been reproduced in elegant in vitro studies (13–15). In the case of actomyosin gels, the contractile stresses arising from molecular motors have been shown to create large actin flows that can reorganize the cortex (16, 17). Because actin filaments and motors are “self-advected,” or transported, by their own flow (18), there is a self-reinforcing loop in gel density, capable of creating patterns. Nevertheless, most theoretical studies do not consider the cross-effects of polymerization and diffusion, which resist pattern formation. Interestingly, in the past years, several groups have reported in vivo examples of actin patterns: mammalian axons (19), Caenorhabditis elegans embryo (20), and Drosophila trachea (21) are all cellular cylinders that display a regular array of concentric actin rings on their cortex.

In this article, we study the example of ring formation in the Drosophila trachea and propose a generic mechanism for stable actin pattern formation, arising from the interplay of actin turnover and myosin activity. The model makes clear predictions, which we test through fly genetics and drug experiments.

Formation of Supracellular Actin Rings

In Drosophila tracheal tubules, actin filaments concentrate at the apical cortex. Using Lifeact-mEGFP, which binds actin filaments, we performed time-lapse imaging to characterize the dynamics of actin in the fly tracheal system. At stage 15 of embryogenesis, we observed de novo formation of circumferential supracellular actin rings, from an initially uniform apical cortex, with different actin markers: Lifeact-mEGFP (Fig. 1A and Movie S1) and moesin-GFP (movie S3 of ref. 22). These structures, which face the extracellular matrix (ECM)-filled lumen, became prominent at stage 16 and showed a well-defined period ($0.5\pm 0.1$ μm; n > 150 rings). There are between 15 and 20 rings in one cell, and this pattern is later used as a template to deposit a ring pattern of cuticle (taenidial folds) (21). Using immunostaining, we also detected that nonmuscle myosin II (myosin heavy chain Zip) was enriched at the apical cortex and colocalized with actin filaments (Fig. 1B), although the pattern was not as clear. Rings were also present later at the third-instar larval stage (21, 23), in the air-filled trachea, with a larger, but still regular wavelength period ($1.2\pm 0.1$ μm; n > 150) (Fig. 1C and SI Appendix, Fig. S1). The appearance of actin rings coincided precisely with a $60\text{\%}$ increase in filamentous actin concentration, referred to simply as actin in the rest of the manuscript (Fig. 1A), as measured through Lifeact-mEGFP. As increased actomyosin concentrations correspond to increased contractility (18), we therefore proposed a minimal model of the actomyosin cortex, where a contractility-driven advection–reaction instability drives regular actin pattern formation (Fig. 1D).

Fig. 1.

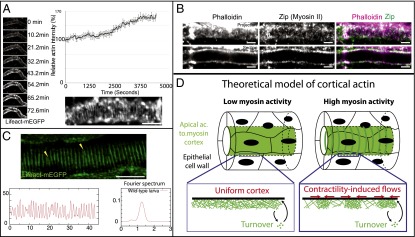
Periodic supracellular actin rings in tracheal tubular system. (A) Live imaging of actin dynamics during the formation of the pattern, using Lifeact-mEGFP. Actin intensity increases by $70\text{\%}$ at the onset of ring formation. (Bottom Right) Enlargement of actin ring structure (phalloidin) at embryonic stage 16. (B) Actin (phalloidin) and myosin II heavy chain (Zip) in the tracheal tubular system at stage 16. (C) At third-instar larval stage, the actin rings (in green, fixed sample) are very regularly spaced, as can be seen in the intensity profile and in the Fourier spectrum, with a period of 1.2 μm. (D) Theoretical model of an actomyosin cortex as a viscous and contractile gel, undergoing turnover and in frictional contact with an ECM. An instability into periodic patterns in actin concentration is very generically expected due to myosin contractility. (Scale bars: 10 μm.)

Theory of Actin Pattern Formation

We first concentrate on understanding the formation of actin stripes within a single cell and restrict ourselves to patterns displaying radial symmetry. We thus consider the cell cortex as a finite one-dimensional (1D) (of length L, in the axial direction x), compressible, viscous, and contractile actomyosin gel, in frictional contact with a rigid substrate. The conservation equation for the actin gel of density ρ reads as follows:

$${\partial }_t\rho =\frac{{\rho }_0-\rho }{\tau }-{\partial }_x\left(\rho v\right)+D{\partial }_{xx}\rho ,$$ [1]

where τ is the turnover time of actin treadmilling around a reference density ${\rho }_0$, and D is an effective diffusion coefficient, whose physical origin we discuss in SI Appendix. This equation expresses that changes in actin concentration over time (left-hand term) arise from three contributions (from left to right in the right-hand term): actin turnover, advection by cortical flows, and effective diffusion of filaments.

Momentum balance in the gel and constitutive behavior at linear order in the gel density around the reference state, respectively, read as follows (8):

$${\partial }_x\sigma =\xi v\hspace{1em}\sigma ={\chi }^0\rho /{\rho }_0+\eta {\partial }_{x}v,$$ [2]

where σ is axial stress in the network and v is velocity. ξ is the friction coefficient with respect to the substrate; ${\chi }^0$, the contractility arising from myosin motors; and η, the gel viscosity. As detailed in SI Appendix, we assume that myosin is in excess, with fast turnover, and therefore simply follows actin concentration. Starting from an initially uniform density ρ, a patterning instability occurs when myosin contractility reaches a threshold ${\chi }_c={\left(\sqrt{\eta /\tau }+\sqrt{D\xi }\right)}^2$ and forms a stationary pattern at a wavelength:

$${\lambda }_c=2\pi {\left(\frac{D\tau \eta }{\xi }\right)}^{1/4}.$$ [3]

Therefore, as expected, high diffusion, friction, viscosity, or a low turnover time τ all stabilize a uniform cortex, by increasing the contractility threshold for pattern formation. The influence of each parameter on the wavelength is more complex: higher diffusion, viscosity, and turnover time favor large wavelengths, whereas a higher friction favors small wavelengths. These criteria are similar to ref. 24, which investigates in a different setting the temporal size oscillations of apical cell areas. The case $\tau \to \infty$ has been studied theoretically previously (10, 11) and yields to actin accumulation in a single region. We can therefore define two characteristic length scales crucial for the patterning:

• $l_h=\sqrt{\eta /\xi }$ is the hydrodynamic wavelength, i.e., it quantifies the length at which contractile stresses are propagated in the cortex. For lengths larger (respectively, smaller) than $l_h$, the flow is dissipated by friction (respectively, viscosity).

• $l_t=\sqrt{D\tau }$ compares the range at which diffusion and turnover act. On lengths larger (respectively, smaller) than $l_t$, a change in concentration is relaxed dominantly through turnover (respectively, diffusion).

We adimensionalize the equations (SI Appendix). Our model then involves only three nondimensional parameters: $\alpha =l/l_h,$ which reflects the size of a cell with respect to the hydrodynamic length scale, $\chi ={\rho }_0{\chi }^0/\xi D$, which measures the importance of contractility-induced flows favoring the localization of the gel and $\varphi =\eta /D\tau \xi$, which is the ratio of viscous stress created by actin turnover over frictional stress created by random diffusive motion. We performed a detailed analysis of the bifurcation diagram (SI Appendix, Figs. S9–S12) of this system, which demonstrates the pertinence of the linear analysis, as well as a numerical analysis confirming our analytical predictions (SI Appendix, Figs. S13–S15).

We also incorporated in our model the 2D geometry of the cortex, neglecting the effect of curvature as a first approximation and modeling the tube as a 2D periodic strip. In the absence of any polarizing, isotropic labyrinth patterns are formed as expected. Nevertheless, as the ECM is composed of chitin fibers oriented predominantly in the axial direction (25), and as cells themselves elongate preferentially in the axial direction as well (26, 27), we examine the effect of an anisotropic friction coefficient ${\xi }_i$. For orthoradial frictions slightly larger than axial frictions $\left({\xi }_{\theta }>1.1{\xi }_z\right)$, circumferential actin rings are formed (Fig. 2E). We observe that defects remain in the simulation at steady state, closely mirroring the actual ring reconnections (Fig. 1C), and causing the formation of local spirals on small step size, instead of rings. Interestingly, the isotropic labyrinth patterns resembles closely the actin organization in DAAM mutants as reported in ref. 21.

Fig. 2.

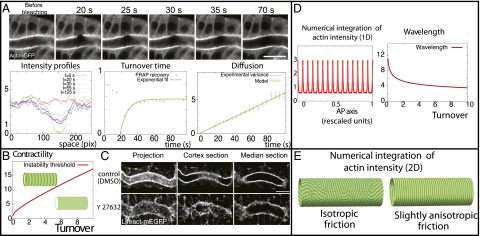
Theoretical predictions and validation of the model’s key assumptions. (A) Fluorescence recovery after photobleaching (FRAP) experiments on the apical cortex (marked by Actin-GFP) just before ring formation. We measure both the turnover time and the diffusion coefficient of the actin gel from the recovery curves. (B) Phase diagram of the instability. A cortex is predicted to organize into periodic patterns as soon as the rescaled contractility χ is above a critical value, which increases with the rescaled turnover ϕ. (C) Actin patterns at embryonic stage 16 disappear with contractility inhibition (through incubation of 250 μM Y27632), as predicted by our model. (D) Theoretical profiles of actin concentration for different values of our parameters in 1D. (E) In 2D, if all parameters are isotropic, labyrinth patterns are formed (Left), but circumferential rings are formed for small anisotropies (Right, where the friction coefficient ${\zeta }_{\theta }$ is increased by 20% in the orthoradial direction). (Scale bars: 10 μm.)

Testing the Model

Validation of the Model Hypothesis.

First, we performed fluorescence recovery after photobleaching (FRAP) experiments to measure some of the parameters that we use, and validate our hypothesis of the cortex as a viscous, active gel undergoing turnover. When we bleached a large region in the cortex at the embryonic state, we observed a rapid and uniform recovery of fluorescence, which can be well fitted by a single exponential (Fig. 2A and Movie S2), which is what is predicted by Eq. 1 (see SI Appendix for details). This allowed us to estimate the turnover time $\tau =15\pm 7\hspace{0.17em}\text{s}$ (n = 10), which is consistent with previously reported cortical turnover times (28). The immobile fraction is typically small (<20% in our experiments).

To extract the diffusion coefficient as well, we monitored the variance of the concentration profile after photobleaching (29) and showed that it increased linearly in time (Fig. 2A, Bottom Right), as predicted quantitatively by Eq. 1 (see SI Appendix for details). The diffusion coefficient that we extracted is D = 0.04 ± 0.03 μm²⋅s⁻¹ (n = 10). Therefore, these experiments allow us to calculate the characteristic length l_t ≈ 0.8 ± 0.5 μm in this system, close to the measured ring wavelength of 0.5 ± 0.1 μm.

Estimating the hydrodynamic length $l_h$ is more difficult in this system, and can be considered as the one fitting parameter to match the observed wavelength. Assuming a friction $\xi ={10}^9$ Pa⋅s⋅m⁻¹ (30), a cortical thickness of 100 nm (28), and a viscosity ${\eta }_{3D}=\eta /h={10}^2$ Pa⋅s, as reported in ref. 31, we can then estimate the hydrodynamic length to $l_h\approx 0.1$ μm. This predicts a wavelength for the pattern near the threshold of ${\lambda }_c=1.8$ μm, which is slightly larger, although of the same order of magnitude, than the data for embryonic and larval trachea. One should note that this is only the wavelength at the threshold, as the ring spacing is predicted to decrease as contractility increases (SI Appendix).

Now that we validated the basic hypotheses of our model, we then tested its two main predictions: that the instability is contractility dependent, and that the wavelength of the pattern can be modified by modifying the physical properties of the gel described above.

Model Predictions.

To verify the first prediction, we incubated the embryos with 250 μM Y-27632, a drug widely used to decrease myosin II contractility, by inhibiting the Rho-associated protein kinase (ROCK) (32). Strikingly, the actin ring pattern disappeared (Fig. 2C), indicating that myosin contractility is essential for its formation and maintenance. This also reinforced our hypothesis that the observed increase of actin intensity at stage 14–15 is the trigger of pattern formation.

For the second prediction, we can note from Eq. 3 that decreasing the friction coefficient ξ is predicted to increase the wavelength of the pattern, because cortical flows can propagate on larger scales. Friction can be expected to arise from several contributions, and in particular from the linkage of the cortex to the ECM via the adhesion complex. We therefore expected that genetically modifying cortical adhesion should modify the ring spacing.

We start by examining mutants for Src42A, which is involved in the stabilization of the adhesion complex (27), interacting with E-Cadherin and β-catenin, being important for adhesion turnover and homeostasis. Src42A and its associated protein, formin family F-actin nucleator DAAM1, have also been shown to affect axial cortical tension and to induce aberrant phenotypes in tracheal development (26, 27, 33). In Src42 mutants, the ring structure is still clearly visible (Fig. 3A), but the period is $0.8\pm 0.2$ μm, a $70\text{\%}$ increase compared with the wild type (Fig. 3B; $n>110$ rings for each; $P<{10}^{-10}$; counted on at least five different tracheas). Moreover, we examined the effect of down-regulation of moesin, the key linker between cortex and membrane in Drosophila (34), by expressing moesin RNAi in trachea. Actin patterns are severely in embryos and larvae (SI Appendix, Fig. S1 A and B). Because taenidial folds are precisely complementary with actin pattern (SI Appendix, Fig. S2), we measured the wavelength of taenidial folds in moesin RNAi larvae and found a 25% increase compared with wild type ($1.8\pm 0.5$ μm vs. $1.45\pm 0.3$ μm; $P<{10}^{-10}$; $n>250$ patterns for at least four trachea in each condition), in agreement again with a decreased friction in moesin RNAi.

Fig. 3.

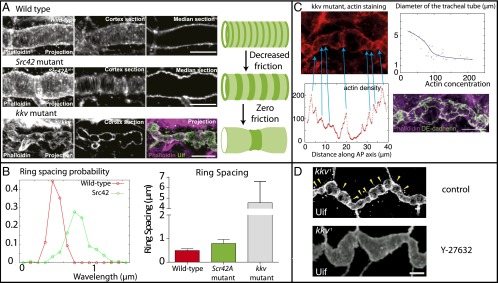
Model predictions tested through pharmacological perturbation and fly genetics. (A) The period of the ring pattern increased by 70% in Src42 mutants, and 10-fold by genetic removal of the extracellular matrix inside the tube (kkv mutant). One of our model’s core predictions is that decreasing friction should increase the wavelength of the pattern. (B) Wavelength increases in Src42 and kkv mutant $\left(P<{10}^{-10}\right)$, compared with wild type. (C) Local constrictions are observed in kkv mutants lacking an ECM substrate and colocalize with actin (phalloidin staining), and high actin concentration correlates with small tube radius, showing that the rings are contractile. (Bottom Right) Cadherin (green) and actin (purple) stating, showing that only one actin ring is present per cell on average. (D) Actomyosin constrictions in kkv mutant disappeared by lowering contractility through Y-27632 treatment. (Scale bars: 10 μm.)

Moreover, the friction is dependent, not only on linkage molecules, but crucially on the presence of a solid ECM substrate to adhere on. In a previous work, we have indeed shown that, at that stage, a chitin/Dumpy matrix core is assembled at the center of the tube and behaved like an elastic solid on timescales of hours (25). In the absence of a solid ECM, we expect the friction coefficient to be drastically reduced, as only a small effective friction remains, arising from the viscous flow of the cytosol permeating through the gel, as discussed extensively in ref. 35. Moreover, for a finite-size system (i.e., one cell length L), the wavelength cannot be infinite, so as soon as it is larger than the cell size $\left(\lambda >L\right)$, we expect that actin should accumulate in one single spot (i.e., one actin ring per cell).

To verify this prediction, we investigate the chitin synthase Krotzkopf verkehrt kkv¹ mutants, where the formation of the chitin/Dumpy matrix core is impaired (36) (Fig. 3). At stage 15, where rings should normally form, the tube develops an aberrant “pearling” phenotype, characterized by a series of large constrictions. We displayed on Fig. 3C examples of this phenotype, stained for phalloidin and DE-cadherin. The constrictions colocalize with rings containing both actin (Fig. 3C) and myosin II (SI Appendix, Fig. S3). We can therefore hypothesize that the actomyosin-generated stress in this region is large enough to locally constrict the tube, in a very similar manner to a cytokinetic ring in dividing cells (17) and nondividing notochord cells (37). This effect is amplified by the fact that there is no elastic chitin anymore in the center to resist the constriction. To test this quantitatively, we measure simultaneously along the length of the tube the local diameter, as well as the local average actin density (Fig. 3C). This reveals a robust anticorrelation between the two: constricted regions have large actin densities, whereas enlarged regions have low actin densities. Moreover, we incubated kkv mutant embryos in 250 μM Y-27632. The tube uniformly dilated, which is expected from Laplace law by reducing the tension (Fig. 3D). As expected, we also observed that most of the constriction disappears (except at the fusion points between the main trunk and the side branches), proving that the actomyosin rings we observe are contractile as assumed in the model. Although the actin rings are no longer as periodically arranged, we can still measure a characteristic distance of $4.5\pm 2$ μm between each ring (n > 40; Fig. 3B) and observed that this corresponds indeed on average to one ring per cell (Fig. 3C).

Dynamical Properties of Actin Rings

Moreover, we took advantage of this kkv mutant, where the spacing is larger, to resolve better the live dynamics of the actomyosin rings. We took time-lapse images of tracheal tubes labeled by moesin-GFP, both in wild type and in kkv mutants. To our surprise, the live imaging revealed unexpected dynamics, with constrictions being extremely dynamical in time, and moving along the trachea in a disorderly manner (Fig. 4 A and B, and Movie S3).

Fig. 4.

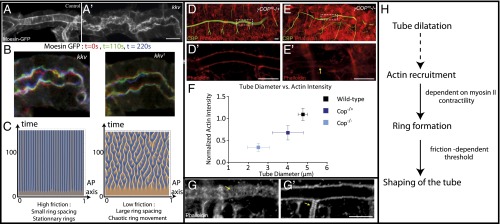
(A) Live imaging of rings in control tracheas using moesin-GFP. (A′) Live imaging of rings in kkv mutants using moesin-GFP. (B) Moesin-GFP in kkv mutants. We show three superimposed time steps: t = 0 (green), t = 90 s (red), and t = 180 s (blue), showing that, in kkv mutants, the constrictions are not stationary. (C) Kymograph of patterns in the high- and low-friction regimes, in the case of a nonlinear turnover. A transition toward chaos is observed. (D and E) Heterozygous and homozygous γ-COP mutants. (D′ and E′) Longitudinal section of tracheal tube in heterozygous (D′) and homozygous (E′) γ-COP mutants. (F) COP mutants show a decreased tube diameter, compared with wild type, as well as a decreased cortical actin level. Both phenotypes are stronger for homozygous mutants. (G) Fixed samples of actin (phalloidin) rings in wild type. One can observe that rings form both in the main trunk (G) and in side branches (G′), at the same wavelength. (H) Summary of the proposed model. (Scale bars: 10 μm.)

To probe whether our physical model could reproduce this behavior, we examined the effect of simple nonlinearity to our equation. Surprisingly, adding a small nonlinearity in the turnover rate of actin caused a transition from stationary patterns to chaotic patterns (Fig. 4C), a previously unreported property of such a simple model of active fluid. We numerically drew a phase diagram of this secondary instability and showed that chaotic time oscillation of our patterns occurred only below a critical threshold in friction (SI Appendix, Figs. S5 and S6). Again, this is in agreement with the experiments: lowering friction causes both an increase in pattern wavelength, and a transition from stationary to nonstationary rings. Furthermore, we showed that the patterns in our simulations are truly chaotic (SI Appendix). Although a detailed nonlinear analysis is well beyond the aim of this article, we can give a simple physical argument for the transition at low friction: two neighboring rings can only interact with each other and merge if their distance is lower than the hydrodynamic wavelength. Otherwise, their interaction is screened. This gives a criteria, $\lambda =2\pi {\left(D\tau \eta /\zeta \right)}^{1/4}<{\left(\eta /\zeta \right)}^{1/2}$, indicating that chaos can only occur if the friction is lower than a critical value, $\zeta <{\zeta }_c\propto \eta /D\tau$.

We now turn back to the question of the signal triggering actin and myosin recruitment on the apical cortex, which drives the instability. Because this recruitment is concomitant with diametric tube expansion, we hypothesized that this could be a mechanosensitive cue, as it was recently shown that tension on the adherens junctions via α-catenin caused a mechanosensitive recruitment of actin, through vinculin and Mena/VASP proteins (38, 39). We thus examined the small-diameter tube mutant γ-COP (40), which cannot enlarge due to impaired apical secretion. The phenotype is less severe for the heterozygous mutant (cop^+/−) than homozygous (cop^−/−) (Fig. 4 D and E). Neither mutants display a clear structure of actin rings, which is consistent with the previous report (41) that in mosaic mutants for sec24, encoding a cargo-binding subunit of the COPII complex, the thin part of the tube lacks actin rings. Crucially, we looked at cortical actin levels in wild-type, cop^+/− and cop^−/− embryos (SI Appendix, Fig. S4), and showed a progressive decrease in actin levels as the tube expansion is impaired: cop^+/− tracheas are $20\text{\%}$ smaller than wild type and had $40\text{\%}$ less actin, and cop^−/− tracheas are $45\text{\%}$ smaller than wild type and had $65\text{\%}$ less actin (Fig. 4F). This reinforces our hypothesis that actin recruitment is the driver of the instability and is connected with the widening of the tracheal tube. Interestingly, periodic actin rings were also observable on the side branches of the wild-type trachea (Fig. 4G′) and had the same period as on the main trunk, even though the diameter of the side branches is about three times lower. This argues against a direct influence of tube radius itself on the pattern (12) in this system.

Discussion

By a combination of modeling, genetics, and pharmacological experiments, we have shown that cortical actin patterns can arise de novo through a contractility-dependent physical instability. Because myosin motors are contractile, imbalances in their distribution create hydrodynamical actin flows; and because the motors are advected, a self-reinforcing loop exists, which can generate a sustained steady state of actomyosin flows from an initially uniform distribution. Interestingly, such a mechanism has been theoretically predicted and experimentally shown to be at play to drive amoeboid cell migration in zebrafish embryonic progenitor cells (11, 42). This corresponds to our low-friction limit, where only one actin accumulation forms in the cell.

Nevertheless, our analysis proves that, generically, other modes of the instability can be seen, for high frictions or lower turnover rate for instance, and result in a patterned actin cortex of well-defined wavelength. Although this instability is qualitatively different from Turing’s original ideas, it demonstrates the increasing relevance of hydrodynamical approaches to study developmental (5) and biological problems in general (7). A strength of our model is that it provides a clear physical basis for pattern formation, as the wavelength of the pattern is dictated by the physical properties of the actin gel, which are a priori all measurable experimentally in a variety of conditions (18). A key question that remains, however, is how the orientation of the pattern is regulated, to form rings in the circumferential direction, given that several mutants can cause formation of other types of pattern orientation, at constant wavelength (21). Curvature in particular could be a geometrical cue that cells are able to read and adapt to. Another aspect that deserves future attention will be the supracellular coordination between actin rings. As long as a pattern exists in individual cells, we show (SI Appendix, Fig. S16) for very small couplings, for instance a dependency of junction maturation on stress, as reported in ref. 38, is enough for robust supracellular coupling.

Our live imaging also revealed an intriguing dynamical property of the actin rings, which move around and coalesce without apparent steady state. Our model reproduces this finding, although other contributions could be in play, in particular a coupling between the actin dynamics and the local axial curvature, which is high in the constriction region, similar to the dynamics of FtsZ proteins on cylindrical membranes (43, 44).

Interestingly, several other instances of such periodic cortical patterns have been reported in C. elegans embryos (20) and in mammalian axons (19) through superresolution microscopy. Given the generality of our model, one expects that more examples should be found, provided that the friction is large enough that several patterns can fit in one cell size. In the future, it will be very interesting to study whether our biophysical mechanism applies to them.

Materials and Methods

Fly Strains and Genetics.

UAS-actin-GFP was from Hiroki Oda, Kyoto Research Park, Kyoto, Japan and UAS-lifeact-mEGFP has been described previously (25). UAS-Zip-GFP was from Dan Kiehart, Duke University, Durham, NC. kkv¹ was from the Drosophila Genetic Resource Center in Kyoto. src42^A26–1/CyO was from Kaoru Saigo, University of Tokyo, Tokyo. Moesin RNAi strains (P[TRiP.JF01610]; no. 31135) were from Bloomington Drosophila Stock Center, Drosophila RNAi Project (Transgenic RNAi Project).

Immunofluorescence.

The primary antibodies used in this study were as follows: guinea pig anti-Uif (1:500; a gift from Robert E. Ward, University of Kansas, Lawrence, KS); phalloidin (1:100; Sigma); rat anti–DE-cadherin (DCAD 2) (1:20; Developmental Studies Hybridoma Bank); rabbit anti-zip2 (1:200; a gift from Fumio Matsuzaki, RIKEN CDB, Kobe, Japan); and chitin-binding probe (CBP) (1:50).