Fig. 4.

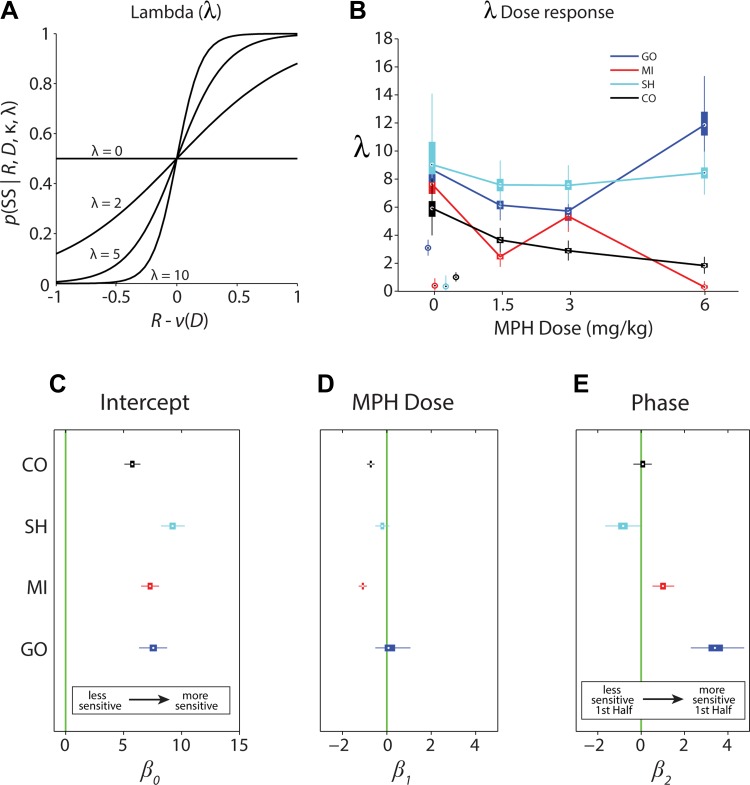
Analysis of choice sensitivity constant (λ). A: examples of choice functions for simulated values of λ. The probability of choice of the SS given a particular size of the SS (R) and delay of the LL (D) plotted as a function of the difference between R and the discounted value of the LL [ν(D)]. This value represents the difference between the axes R and D in Fig. 2, allowing for the collapse of 2 dimensions into a single dimension. When [R − ν(D)] = 0, the so-called indifference point, choices are maximally random [p(SS | R_i,D_i,κ,λ) = 0.5]. As choice sensitivity decreases and λ becomes smaller, choices become more random across all values of [R − ν(D)]. B: choice sensitivity constant (λ) plotted as a function of MPH dose for all 4 subjects. Details as in Fig. 3B. The empirical null distribution medians and 99% confidence intervals of λ resulting from repeated reassignments of the reward-image mappings are shown for each of the subjects under control conditions (data points jittered around 0 mg/kg for clarity). C–E: GLM parameter estimates for λ. Details as in Fig. 3, C–E. C: estimate of intercept (β₀^subject) for the discounting constant, κ. Intercept values indicate subject's average λ value over conditions. D: estimate of the slope of MPH dose effect (β₁^subject) on κ. Slope values indicate the linear trend resulting from varying doses of MPH treatment. E: estimate of the phase effect (β₂^subject), testing for a difference in κ between the 1st and 2nd half of the session.